结构动力学应用中若干基本概念的研究
张开银, 孙 齐, 熊驷东, 蒋紫玲
(武汉理工大学 船海与能源动力工程学院,武汉 430063)
随着科学技术的飞速发展,各种工程结构和供应产品向大型、高速、高性能、高精度和轻结构方向发展,动力学问题也越来越备受重视。在现代工程和结构设计中,必须进行结构动力学分析和动态设计,同时,结构动力学也是结构振动控制、结构动态优化设计、结构可靠性设计、结构健康监测和结构计算机辅助设计等学科的基础。由此应用而涉及到的一些动力学基本概念理解的问题凸显出来。本文就结构位移响应与第一阶固有频率的关系、结构各阶位移模态的贡献与模态应变能的关系、单自由度系统和多自由度系统共振的概念及区别、多自由度系统共振内涵之辨析、结构共振之工程应用等问题进行了深入分析与辨析。
1 各阶位移模态与模态应变能
用谐波分析的方法将周期为T的激振力按照傅里叶级数展开,即
(1)
式中:ω为基频,ωi=iω称为倍频;利用上式可以将一周期激振力分解为一系列频率为iω的简谐激振力,由于线性系统服从叠加原理,因此激振力f(t)总的响应等于各简谐激振力响应之和。
工程上习惯性地称第一阶固有频率为基频[1-2]。由振型叠加原理可知,结构的响应按结构模态振型展开,理论上各阶模态的地位是等同的,其对位移响应的贡献取决于模态参与因子。结构的其他阶固有频率与第一阶固有频率一般不存在倍数的关系;因此,直接地将第一阶固有频率称为基频是不合适的,夸大了第一阶模态在结构动力分析中的地位,强化了“第一阶模态贡献较大而高阶模态贡献较小”的概念[3]。以至于在工程实际中分析结构动力特性时,往往偏重于第一阶模态的分析,而轻视了高阶模态。
根据振型叠加原理,结构的响应可视为各阶模态分量加权之和[4]
u=Φξ
(2)
式中:u为物理坐标阵;Φ为模态矩阵;ξ为主坐标阵。
各阶模态对结构的影响程度分析有待进一步推进,为了更深入了解各阶模态响应与模态应变的关系,现以一横向振动的匀质等截面简支梁为例进行讨论。假定梁的第j阶模态所对应的响应为
(3)
根据初等梁理论,第j阶模态对应的应变能为
(4)
式中:l为梁长;EI为梁的抗弯刚度。
根据式(4),若结构第n阶模态与第m阶模态具有相同应变能时,对应的最大振幅比为
(5)
同理,根据式(4),若梁结构第n阶模态与第m阶模态具有相同的振幅时,对应的应变能为
(6)
为了说明各阶模态对结构的影响,给某简支梁一特定激励,假定其响应仅由第一阶模态与第二阶模态所构成,根据式(4),当结构的第一阶模态与第二阶模态具有相同应变能(∏1max=∏2max)时,结构的第一阶模态对应的最大振幅是第二阶模态的对应的最大振幅的四倍,即(ξ1max=4ξ2max)。往往也是如此,结构第一阶模态的最大振幅比高阶模态的振幅更大,诠释了为什么第一阶模态更容易被观察到也更受重视。而当结构第一阶模态对应的最大振幅与第二阶模态对应的最大振幅相等时(ξ1max=ξ2max),结构第一阶模态对应的应变能仅是第二阶模态对应的应变能1/16(∏1max=1/16∏2max)。所以,低阶模态具有较大的位移,并不一定具有较大的应变能,在进行结构动力特性分析时,不能过分偏重低阶模态而轻视高阶模态。
2 多自由度系统的模态叠加计算
2.1 模态位移法
如图1所示,四个自由度结构的抗剪模型,其剪切刚度系数及楼板质量均表示在图1中,在顶层受一水平力pcos(Ωt)。
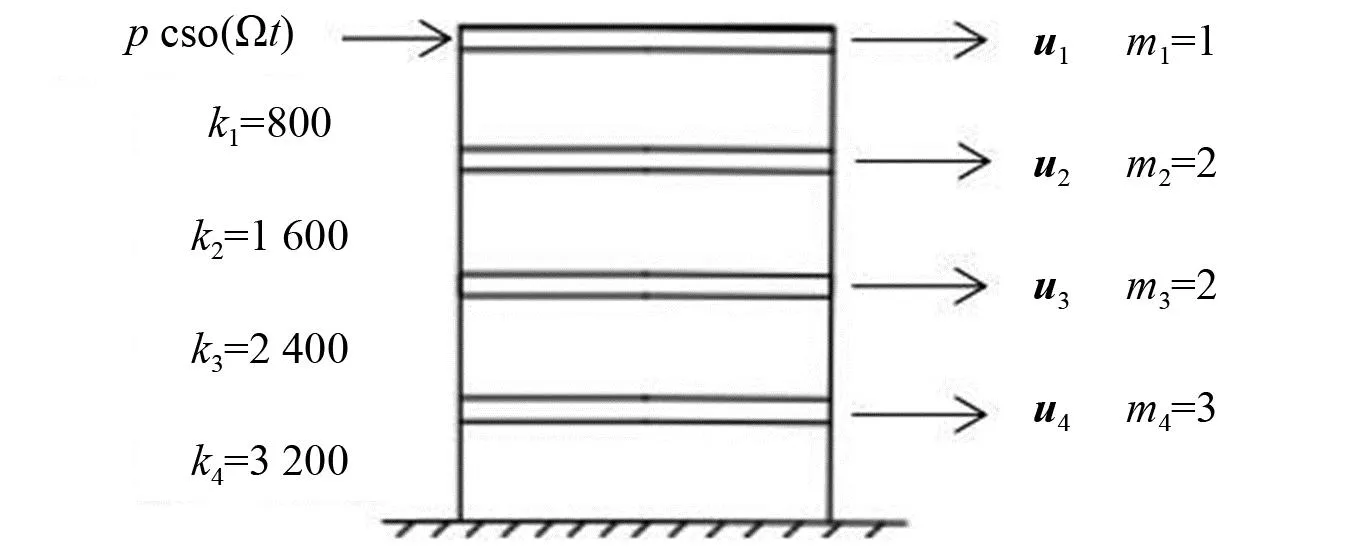
图1 四自由度结构抗剪模型
计算分析系统的固有频率,模态矩阵,模态质量,模态刚度,模态力,以及系统在不同的激振频率下用不同的截断(即N=1,N=2,N=3,N=4)方法的响应振幅。选各层的水平位移u1,u2,u3,u4为广义坐标,根据达朗贝尔原理可列出系统的运动方程为

式中:m为各楼板质量;k为剪切刚度系数;u为各层的水平位移;M为质量矩阵;K为刚度矩阵;F为荷载向量。其固有频率即模态矩阵可用后面的求广义特征值和特征向量的方法获得
其各阶振型如图2所示。
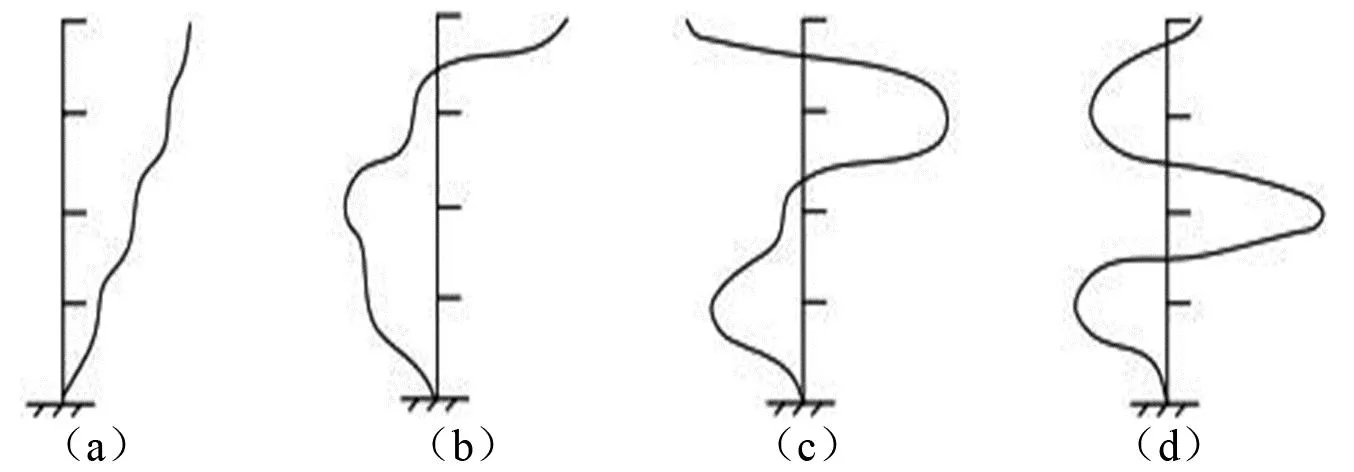
图2 各阶主振型
求得模态质量,模态刚度和模态力为
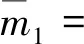
模态刚度可以从上式求得,也可用更简单的方法求得,即
其余的模态质量,模态刚度可用相似的方法求得,即
模态力
因系统是单点简谐激励。而且要求u1的稳定响应幅值,可直接用公式,并表明各阶模态的影响,有
对Ω=0.5ω1,Ω=1.3ω3,其u1的幅值(pcos(Ωt)的系数)计算结果如表1所示。

表1 u1幅值计算结果
从上述结果可以看出,只取第一阶模态在3个激振频率下都是不精确的,误差太大。取前3个模态在激振频率为0或0.5ω1时,其响应已足够精确,但是对Ω=1.3ω3,误差仍然较大,其原因是此时的激振频率几乎等于ω4,那么对u1的响应贡献最大者应是第四阶主模态,所以此时不能截断第四阶模态。
2.2 模态加速度法
因ζ=0可得

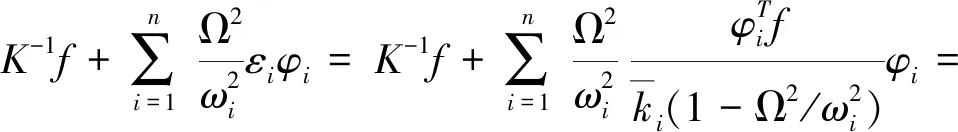
于此得
于是
分别给出Ω=0,Ω=0.5ω1,Ω=1.3ω3的情况下,取不同阶数时对u1的振幅影响,如表2所示。
从上述结果可看出:
(1)当Ω=0时,不需要各阶模态的贡献,就可以得到精确的静态解。
(2)在低频激励时,如Ω=0.5ω1,即使取一阶模态就已足够精确,模态加速度法取前两阶模态就和模态位移法的取三阶相当。
(3)当激励频率Ω=1.3ω3时,因为在ω3和ω4之间,在这种情况下,模态位移法和模态加速度法的任何截断都会有较大误差,都需要取四阶模态。
3 单自由度系统与多自由度系统共振分析
多自由度系统或弹性结构的共振,是结构振动理论中一个最基本且十分重要的概念,相关教科书及文献资料中尚未给出完整准确的定义。对于单自由度系统而言,当激励力频率接近或等于系统固有频率时,其位移响应将迅速增大,这种现象被称为单自由度系统的共振[5](教科书中有明确定义)。这一共振概念现已被结构工程界普遍接受,可谓是根深蒂固。如果将单自由度系统共振的概念,不假思索而无条件地拓展到多自由度系统或弹性结构中(即当激励力频率接近或等于系统的某阶固有频率时,结构振幅过大的现象称为结构共振),其科学性与严谨性尚值得商榷。
3.1 单自由度系统共振
对于有阻尼单自由度系统,激励力作用下的振动微分方程为
(7)

系统则以激励频率Ω振动,其稳态位移响应为
y(t)=Ysin(Ωt-α)
(8)
将式(8)代入式(7)得
(9)
(10)
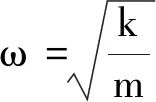
将动力放大系数定义为
(11)

3.2 多自由度系统共振
对于具有比例阻尼[C]=α[M]+β[K](α、β为结构实测资料识别的系数)的n自由度系统,简谐激励力作用下的振动微分方程为
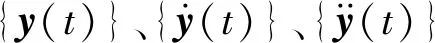
作坐标变换
{y(t)}=[Φ]{ξ(t)}
(13)
式中:[Φ]=[{φ}1,{φ}2,…,{φ}n]为模态矩阵;{ξ}={ξ1,ξ2,…,ξn}T为模态坐标(或模态参与因子)。
将式(13)代入式(12)可得到n个模态坐标解耦的微分方程
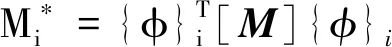
由式(14)可知:其类似于有阻尼单自由度系统强迫振动微分方程,且有
(15)
(16)
式中:ωi为系统第i阶无阻尼固有频率;ζi为系统第i阶模态阻尼比。
由式(15)和式(16),对式(14)作归一化处理可得
对于式(17),若初位移与初速度均为零,运用Duhamel积分,则各阶模态坐标为

将式(18)代入式(13),则多自由度系统的位移响应可表示为
(i=1,2,…,n)
(19)
由式(18)和式(19),若模态荷载Fi(t)≠0而Fj(t)=0(j≠i)时,模态参与因子ξi(t)≠0,ξj(t)=0(j≠i)则系统呈现为第i阶模态,即所谓的纯模态。
那么由模态的正交性,若{P0}=[M]{φ}i,则有
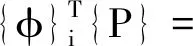
(20)
同理,若{P0}=[K]{φ}i,则有
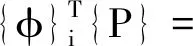
(21)
由式(20)和式(21)作进一步拓展,若激励力满足
{P0}=(a[M]+b[K]){φ}i(a,b为任意常数)
(22)
则系统呈现为第i阶纯模态振动。

4 多自由度系统共振之内涵
实现多自由度系统的共振,在满足激励力频率等于系统某阶固有频率的同时,还要对结构的多点激励进行合理的调制,以保证系统的响应呈现出相应的单一模态。多自由度系统共振之内涵,可以从数学与力学两个方面来准确理解。

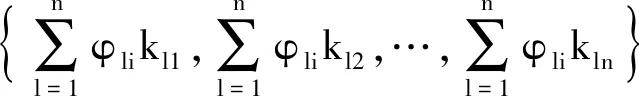
(23)
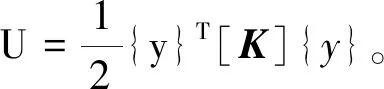
(24)
鉴于多自由度系统各阶模态关于刚度矩阵和质量矩阵的加权正交,各模态间的模态能量不能够相互传递或转移。那么,由激励力输入给系统的各阶模态能量一部分被模态阻尼所耗散,而另一部分用于维持该阶模态的振动。由于系统各阶模态的存在(取决于模态参与因子ξj(t)≠0),结构任一处的响应都将受到各阶模态的相互牵连与制约,有些部位的位移响应得到加强,而有些部位的位移响应受到削弱,从而限制了结构位移响应的进一步增大。而对于呈现纯模态的多自由度系统,各点的响应彼此协调,类似于一单自由度系统的振动。
通过上述分析,单自由度系统共振与多自由度系统共振之区别在于:单自由度系统共振仅仅依赖于激励频率——激励频率等于系统固有频率(没有振型的概念);而多自由度系统共振不仅有赖于激励频率——激励频率等于系统某阶固有频率,更重要的是实现多个激励力分布的合理调整,使其响应表现出纯模态(对结构振型有限制)。正是由于绝大多数结构工程技术人员缺乏对结构动力学基本概念的准确理解,将单自由度系统共振之概念无条件地拓展到了多自由度系统与连续体的振动中。通过对结构共振概念的辨析与讨论,以保证其科学性与严谨性。
5 结构共振之工程应用
多自由度系统或结构共振概念的辨析,不仅在于准确理解结构动力学的基本概念;同时,在结构试验模态分析中,结构共振(纯模态)状态对于模态参数的识别有着十分重要的工程实用价值[7-9]。
目前,结构试验模态分析中结构模态参数的识别主要分为频率域识别法和时间域识别法,其对结构试验工程技术人员的理论储备和专业素质要求相对较高。如果在结构模态试验时,通过合理调节多个激振的分布和大小来补偿结构的内部阻尼,以便激励出结构的等效无阻尼固有模态。当结构处于纯模态状态振动时,可通过物理测试直接高精度识别出结构的模态参数(如结构固有频率、位移模态、模态阻尼比等)[10],从而可取得事半功倍的效果。参数同步优化随机共振方法可以有效地从强背景噪声中检测出微弱故障信号[11]。在周期荷载作用下,小的外部激励可以激发框架结构的大振幅自参数共振[12]。
在结构试验模态分析中,“共振法”相对于常用的频率域识别法或时间域识别法而言,具有物理概念清晰、模态参数识别精度高等优点。同时,若仅当激励力频率等于结构的某阶固有频率时也被视为结构的“共振”,任一结构的“共振”将会呈现出多种形态(有赖于激励方式而非唯一性),所识别模态参数的精度也有赖于其它模态参与的程度。
6 结 论
(1)根据模态叠加原理,系统的响应由多阶模态的贡献所构成,当激励频率不同时,各阶模态对应系统位移响应的贡献也不同。
(2)多自由度系统或结构的共振,在保证结构振动频率(为某阶固有频率)等于激励频率的同时,其位移响应还应呈现出相应的纯模态。
(3)实现多自由度系统或结构纯模态共振,可用于精确识别结构的模态参数(如结构固有频率、位移模态、模态阻尼比等)。

