尺规操作悟规律 事实演绎推结论

申思 顾晓东

【课前思考】

“三角形的三边关系”是苏教版小学数学教材四年级下册第七单元中的教学内容。“三角形任意两边长度的和大于第三边”是三角形边的重要性质，也是本单元的教学难点。主要引导学生任意选3根小棒进行围三角形的操作实验，探索发现三角形的三边关系。《义务教育数学课程标准（2022年版）》（以下简称“新课标”）对本课教学给出了新思路，主要体现为两点：一是利用尺规作图方法探索三角形任意两边之和大于第三边，二是从已知的基本数学事实出发说明三角形的三边关系。尺规作图是直观几何向欧几里得几何过渡的重要桥梁，利用尺规作图选作三角形，能让学生充分经历在严谨的几何操作实践中逐步感悟、发现数学命题的过程。进而再从已知的“两点之间线段最短”这一基本事实出发，通过演绎推理说明数学命题的正确性，从而培养学生初步的推理意识。在“新课标”理念的指导下，我们在课前先安排四年级学生认识圆、使用圆规，指导学生掌握尺规画三角形的技能，进而对现行苏教版小学数学教材中“三角形的三边关系”一课进行新的教学尝试。

【教学过程】

一、创设情境，激活旧知，引出问题

1.情境激旧知，引出事实

师（呈现去体育中心打羽毛球的情境图，如图1）：从体育中心大门口到羽毛球馆有两条路，走哪条路最近呢？请用学过的数学知识解释一下其中的道理。

生：走下面那条路最近，因为两点之间线段最短。

2.抽象识关系，导入问题

师：图1中除了能看到点和线，还能看出什么？

生：图1中还有三角形。

生：AC+BC>AB。

师：同学们用数学的眼光发现了一个三角形及其三条边之间的一种关系。那么，三角形三条边之间究竟有什么关系呢？今天这节课我们就来研究这个问题。

【设计意图】教师从现实生活出发，提出“选择路径”这一现实问题，并启发学生利用生活原型抽象出几何元素“点”“线”“形”，进而自然引出“关系”。这样的设计能让学生感受数学来源于生活，学会用数学的眼光观察世界，搭建数学与现实世界的桥梁，从而更容易找到新知识的支撑点，既激发了学生的学习兴趣，也为后续探究活动的展开做好铺垫。

二、尺规作图，分层探索，感悟规律

1.初探，完成尺规作图

任务一：3条同样长的线段，能围成三角形吗？

学生从4条不同长度的线段中任选一条，用直尺和圓规画一画，再与同学交流作图方法。

师（课件动画演示）：为什么这样找交点？

生：第一条弧表示弧上任意一点到左端点的距离是4 cm，第二条弧表示弧上任意一点到右端点的距离是4 cm。这个交点到左端点的距离是4 cm，到右端点的距离也是4 cm，所以它是三角形的第三个顶点。

师：如果选择其他长度的线段，也能像这样画出三角形吗？从中你们得出了什么结论？

生：3条同样长的线段，都能围成三角形。

2.再探，完成尺规作图

任务二：3条不同长度的线段，能否围成三角形。

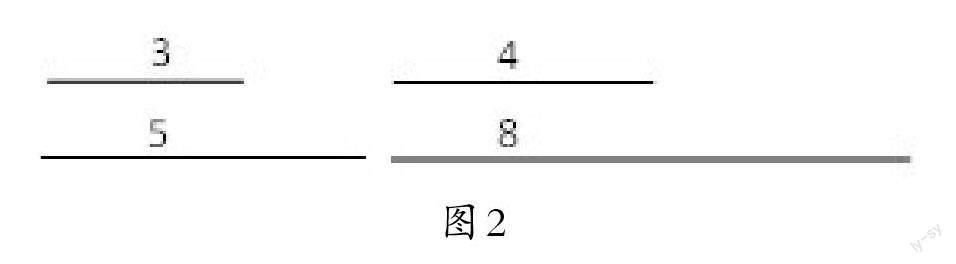
教师要求学生从图2中的4条线段中任选3条，用直尺和圆规画一画，再与同学交流自己的发现。

学生4人小组按序号每人研究一种选法，然后尝试尺规作图，能围成的，画出三角形，并标上数据；不能围成的，画出作图痕迹，也标上数据。

教师组织学生展示作品（如图3）并解释：为什么有的能围成三角形，有的不能围成呢？

生：图3-②，3 cm和4 cm这两条线段太短了，两条弧没有交点，3+4<8，说明3条线段不能首尾相接围成三角形。

生：图3-③，3 cm和5 cm的线段也短了一点，两条弧的交点刚好在8 cm的线段上，3+5=8。把上面两条线段连接起来，刚好与8 cm的线段重合，也不能围成三角形。

生：图3-①，3 cm和4 cm加起来超过5 cm了，两条弧有交点，3+4>5，所以能围成三角形。图3-④和图3-①一样的情况。

【设计意图】数学操作活动可以帮助学生直观地理解数学，感悟数学本质。尺规作图作为学习三角形三边关系的有效抓手，解决了以前课堂中摆小棒引起的误差问题，使活动更加严谨。任务一中的尺规作图画的是等边三角形，旨在复习已学尺规作三角形的方法和原理，并明确3条等长线段能围成三角形；任务二是自由选择3条不同长度的线段利用尺规作三角形，从不同结果中直观感悟、体会“为什么有的能围成三角形，有的不能围成三角形”，并且借助数形结合，帮助学生更清晰直观地发现三角形3条边之间存在的特殊关系。

三、由形到数，多轮观察，逐步归纳

1.由“一般”入手，观察、发现结论

师：观察图形，能围成三角形的3条线段有什么共同特点？

生：能围成三角形的3条线段，两条较短线段长度的和大于最长线段。

师：再来看看不能围成的两种情况呢，可以怎么说？

生：不能围成三角形的3条线段，两条较短线段的长度和小于或等于最长线段。

2.回到“特殊”，检验、拓展结论

师：回头看任务一研究的结果，这里没有较短线段和最长线段，它符合我们刚才得到的结论吗？

生：符合。任意两条线段长度的和都大于第三条线段。

师：你这里的“任意”是什么意思？能具体说说吗？

生：分别把每条线段看成最长的线段，都可以得到4+4>4。

师：你能用一句话说说这3条线段之间有什么关系吗？

生：任意两条线段长度的和都大于第三条线段。

3.再回“一般”，验证、归纳三边关系

师：回过头来看任务二中围成的两个三角形，它们符合“任意两条线段长度的和都大于第三条线段”这个结论吗？

生：符合，3+5>4，4+5>3。

师：通过刚才的一种关系，你们很快地得到了另外两种关系。这两种关系怎么看出来的？

生：可以通过计算得到。

生：5 cm是最长的线段，最长的线段加其中一条较短线段，一定大于另一条较短线段。

师：另一个也是同样的情况。看来“两条较短线段长度的和大于最长的线段”实际上就是“任意两条线段长度的和都大于第三条线段”。

师：再来看任务二中不能围成的情况，你们也能完整地说一说3条线段之间的关系吗？

生：3+4<8，8+4>3。

生：3+8>5，5+8>3。

师：这里也有两条线段长度的和大于第三条线段，为什么不能围成三角形呢？

生：不是任意两条线段长度的和大于第三条线段，就不能围成三角形。

师：这些线段围成三角形以后，它们就变成了三角形的边，由此我们可以得出，三角形任意两边长度的和大于第三边。

【设计意图】从直观经验到抽象概括，是提高学生数学核心素养的必由之路。基于前两次探究活动，学生对3条线段能否围成三角形有了初步的感悟，这为学生后续抽象概括三角形三边关系奠定了感性基础。如何处理“两条较短线段长度的和大于最长的线段”与“任意两条线段长度的和都大于第三条线段”之间的关系，是本节课的关键。教师从形入手，对数进行分析、对比，多次追问、制造认知冲突，用等边三角形化解“任意”这一难点，引导学生在“一般—特殊—一般”之间走个来回，经历“思考—交流—验证—归纳”的思维过程，让探究活动富有层次性和挑战性，促进了深度学习的发生，发展了几何直观和抽象概括能力。

四、动态验证，事实演绎，说理推导

1.几何画板动態演示，估算验证发现

师：对于任何一个三角形，3条边之间都有这样的关系吗？

（教师出示几何画板，任意拉动顶点）

师：不管变成哪种三角形，3条边之间的关系会不会改变呢？

生：不会。

（学生举例，估算验证）

师：三角形是千变万化的，但是三角形的三边关系是不变的。

2.回归数学基本事实，演绎推导结论

师：我们回到课堂刚开始时的这幅图（如图1），根据AB两点之间线段最短，我们已经发现了三角形的3条边之间的一种关系。如果换两个点观察，还能发现什么呢？

生：观察A、C两点，AB+BC>AC。

生：观察B、C两点，AB+AC>BC。

师：把这3个关系合并成一句话，就是我们今天学习的“三角形任意两边长度的和都大于第三边”。

【设计意图】教学中，为了体现数学的严谨性，教师基于“新课标”要求，尝试让学生开展简单的演绎推理，推导出结论。教师结合课始教学情境，让学生再次从数学事实出发，进行推理分析，学生经历演绎说理过程，能感悟推理结果与上面的研究结果“殊途同归”。这样的设计不仅可以聚焦数学规律的本质，让学生经历数学化的过程，体会数学知识的内在联系，发展推理意识，也凸显了数学与生活的联系，让学生感受到数学源于生活又高于生活。

五、优化习题，变式拓展，延伸认知

1.初步应用，判断说理

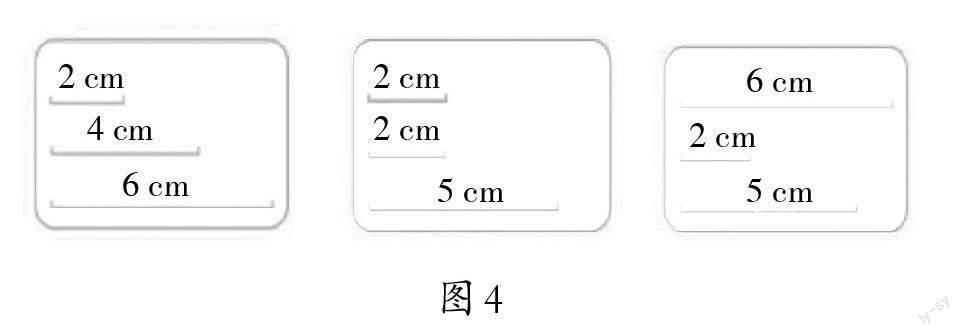
师（出示图4）：哪组线段可以围成一个三角形？说说判断理由。

生：只有第三组可以围成三角形，2+5>6。另外两组最短的两条边的长度和小于或者等于第三边。

（教师引导学生想象尺规作图结果，再以课件出示作图结果）

师：我们来看2cm、2cm、5cm这个情况，如果改变其中一条线段的长度，你们能使它们围成一个三角形吗？如果要围成一个等腰三角形呢？

生：把5 cm变成1 cm或3 cm。

生：把一条2 cm的线段变成5 cm，就能围成等腰三角形。

2.变式应用，明确范围

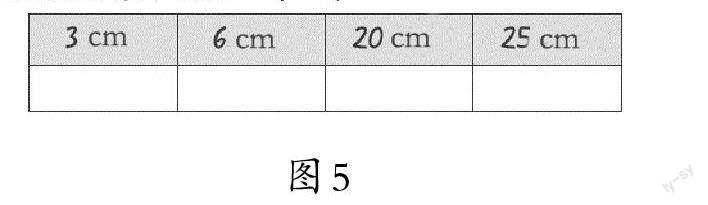
教师课件出示习题（如图5），学生逐一判断说理。教师追问：第三条边除了可能是6 cm，还可以是多少？

生：可以是5 cm、7 cm、8 cm……也可以是小数。

（教师课件动画演示第三条边的各种可能，得到范围：4<x<20，如图6所示）

3.拓展延伸，体会价值

师：在一个三角形中，一条边的长度为12 cm，其余两条边的长度和是14 cm。这两条边的长度分别可以是（    ）cm和（     ）cm？

生：可能是7 cm和7 cm、6 cm和8 cm，也能取小数。

师（动画演示整数和小数的各种情况）：这些答案中有没有隐藏的规律呢？把三角形的第三个顶点连起来会得到什么图形？

生：椭圆。

师（课件播放木工画椭圆的视频，如图7）：智慧的木工师傅就是运用这样的知识画出椭圆的。

【设计意图】巩固应用环节中设计了“判断”“变式”“拓展”三个层次的应用，由浅入深、由易到难，不仅考查了学生对“任意”两字的理解，更考查了学生用数学知识解决实际问题的能力，既融入了本课知识，又结合了椭圆的实际应用情况，让学生充分感受数学知识的应用价值，激发学生学习数学的兴趣。

【课后反思】

一、尺规操作体验感悟，发展几何直观

数学操作活动具有直观性和操作性，能帮助学生积累数学活动经验，是发展数学思维能力的重要载体。本节课一共经历了两次操作活动：第一次是借助尺规画一个等边三角形，借机复习已经学过的尺规作图的方法和原理，便于在后面的探究活动中进行迁移。第二次是用尺规判断不同长度的线段能不能围成三角形，由此引出全课的核心环节，从特殊到一般，让学生初步感知三角形的3条边之间存在一定的关系，通过观察、猜想、操作、计算、想象、说理等方法分析问题，渗透数形结合、变中有不变等数学思想方法，完整经历数学知识的发现过程，积累数学活动经验。在之后的教学环节中虽然不再进行动手操作，但是在推理论证、练习提升中，要么时刻结合操作结果，要么想象或动态演示尺规作图结果，始终关注学生的操作体验。学生经历了完整的几何操作过程，能在关联性、整合性、逻辑性的数学学科实践活动中发展几何直观。

二、基于事实演绎说理，培养推理意识

推理意识主要是指对逻辑推理过程及其意义的初步感悟。学习是一个内化的过程，教师应善于引导学生在面对新的挑战、新的问题时，能自主地关联已有的知识结构和已有经验，结合多元表征寻找最优方案，并将新旧知识进行联结整合，进而把握数学的本质。本课培养推理意识主要体现在引导学生从生活经验出发，演绎推理说明结论。在学生经历观察、想象、操作、说理、验证、反思的过程，并找出三角形三边关系的一般性结论后，回到课堂导入的教学情境，通过变换不同的观察点，引导学生发现三角形三边关系与“两点之间线段最短”这一基本事实是相通的。这样的学习过程实现了直观操作到抽象推理的思维跨越。

（作者单位：江苏省无锡市育英实验小学 江苏省无锡市滨湖区教育研究发展中心）