船舶尾轴承倾角及磨损对水膜压力影响分析

周维新 赵 耀 袁 华＊ 王晓强 王 康

（1. 华中科技大学 船舶与海洋工程学院 武汉 430074； 2. 海军工程大学 舰船与海洋学院 武汉 430033；3. 中国舰船研究设计中心 武汉 430064）

0 引 言

轴承是保证船舶推进轴系正常运转的重要构件。水润滑赛龙轴承由于其环境友好、易装卸、结构简单等优点而在船舶推进轴系中广泛应用。在使用过程中，水润滑轴承能够随着旋转轴的转动形成1 层水动力润滑膜，避免旋转轴与轴承的直接接触，大大降低两者之间的摩擦力，从而有效减小轴承磨损速率[1]。

但是，多艘船舶在维修时发现尾部水润滑轴承的使用寿命远低于设计值，说明轴承的实际磨损量远大于允许磨损量[2-3]。图1 所示为某船尾部水润滑赛龙轴承的磨损情况，该轴承的磨损量已经超过3 倍最大允许磨损量，而工作时间却仅为设计寿命的1/5。轴承寿命的计算方式为允许最大磨损厚度除以轴承磨损速率，而经调查发现该轴承的磨损速率是在理想情况下测试获得（即在轴承无磨损状态下，且轴与轴承之间无倾角），但在实际情况中，船舶由于内外载荷的作用，总是存在一定的变形，故使轴承存在一定的倾角。另外，由于旋转轴反复启停，轴承的磨损难免会日益严重。因此，在船舶下水运行后，轴承存在倾角与磨损才是更接近实际的工作状态。

图1 某船尾部水润滑轴承磨损情况图

20 世纪初期，自橡胶水润滑轴承被使用这后，对水润滑轴承的研究便持续增加。早期的研究多集中于假设水润滑轴承的轴颈与轴承始终是对中状态，且忽略倾角后只需要考虑平面内的流体动压特性。[4]不过随着轴承承受载荷的增大，研究者也开始考虑平面内轴承的弹性变形对流体润滑膜的影响。针对轴承弹性变形的计算，主要采用影响因子系数法，其关键是获得轴承表面的影响系数因子，可分为平面法和非平面法。平面法是将半空间平面受单点集中力的弹性位移解作为影响系数因子，该方法忽略了轴承的几何形状，因此误差较大；非平面法考虑了轴承形状，但求解方法较平面法复杂得多。BLANCO 等[5-6]在研究轮轨接触问题时，针对平面问题的弹性解引入位置修正系数，得到了适用于任意两曲面接触的影响系数因子，然而位置修正系数对于不同曲面有不同的误差。ZHOU 等[7]针对刚性轴与弹性轴承接触，以圆柱壳的单点集中力位移解作为影响系数因子，与有限元方法对比发现精度相差不大但效率更高。更常见的方法是使用有限元方法计算影响系数因子，该方法精度较好，但随着分析轴承的尺寸变化，需要不断重新建立模型，对计算资源要求较高、效率较低。

随着船舶大型化的发展，尾轴承的负载进一步增大，轴承磨损的案例也随之增多，一些学者开始关注轴承倾角对水膜的影响。SUN 等[8]研究了轴的横向弯曲变形对端部支撑轴承的影响，在轴承水膜厚度计算中引入了倾角值，考虑了水膜厚度沿轴向变化带来的影响。张新宝等[9]进一步分析了轴承倾角和摆角同时存在时的影响，结果表明倾角的影响远大于摆角，其建议在安装中采用顺应轴系曲线安装轴承的方法以减小轴承倾角的影响。吕芳蕊[10]提出了考虑表面粗糙度和界面滑移影响的倾斜轴承水膜计算的理论方法。该方法可以有效地分析在实际工作中水膜压力与轴承凸起弹性压力的占比，且结果更接近实际情况。其同时也提出在轴承厚度中间增设弹性层，该结构可以有效缓解倾角对水膜的负面影响。然而上述研究只考虑了轴承倾角的影响，关于厚度磨损对于轴承水膜性能的影响则研究较少。王艳真[11]根据DUFRANE 提出的轴承平面磨损经验公式，分析了磨损对于改性超高分子量聚乙烯水润滑轴承性能的影响。其发现当偏心率较大时，随着轴承承载能力磨损深度增加而逐渐降低。不过，该研究也仅仅考虑了平面磨损的情形。

轴承倾角与磨损同时存在才是船舶水润滑尾轴承的一般工作状态，但是倾角与磨损同时存在对水膜性能的影响还尚无研究。本文基于DUFRANE的平面磨损经验公式，推导了轴承存在倾角与磨损时的水膜厚度公式，引入到考虑弹性变形的水膜厚度计算，并利用有限差分法求解Reynolds 方程获得轴承的水膜压力分布；然后，以某型船舶水润滑尾轴承为研究对象，分析在相同负荷条件下，随着倾角与磨损变化，其水膜压力分布的变化规律。

1 考虑倾角与磨损的水润滑轴承模型

同时存在倾角与磨损的轴承示意图如图2 所示。规定坐标原点位于轴承左端圆心处，沿长度方向为z轴、竖直方向为y轴、水平方向为x轴，并假设轴左端更靠近轴承底部。由于工作过程中尾轴是转动的，因此最小膜厚所在位置会偏离轴承最底端。旋转轴中心点与轴承的中心点连线将与y轴存在偏位角ψ0，规定圆柱坐标系周向坐标θ以该连线为起始点，正方向与旋转轴转动方向ω相同，α是轴与轴承在竖直截面的相对夹角。

图2 考虑倾角与磨损的轴承示意图

图2 中，水膜的厚度分布如式（1）所示：

式中：he为因偏心而引起的膜厚分布，mm；hd为因弹性变形而引起的膜厚分布，mm；hw为因磨损而引起的膜厚分布， mm。

由于轴颈倾角的存在，故不同截面处的偏心距会发生变化，如图3 所示。

图3 不同截面偏心距投影图

对应于不同z坐标截面的偏心距见式（2）：

由此，可得由偏心与倾角引起的膜厚分布he，见式（3）：

式中：间隙差c=R-r，mm；ψz为图3中投影平面内的向量与向量的夹角，rad。

在流体压力的影响下，轴承会产生一定的弹性变形hd，可以通过影响因子系数法求出，如式（4）所示：

式中：i、j、k、l代表有限差分法中对应节点位置编号是影响系数因子，代表节点（θk，zl）处受到节点（θi，zj）处单位力作用的弹性变形。该值通常是通过有限元计算获取，但是计算效率较低。ZHOU 等[7]给出了圆柱壳协调接触时的理论变形解，可省去有限元建模流程，计算效率可提高1 倍。本文的影响系数因子通过该方法获取。

通过对实际轴承磨损的统计分析，DUFRANE指出轴承的磨损通常位于底部且左右对称，并给出了无倾角时的底部磨损经验公式[11]，见式 （5）：

式中：wmax是轴承底端的最大磨损深度，mm。

在考虑轴承存在倾角时，假定该倾角为定值，磨损沿着轴向方向的变化符合线性规律，由磨损引起的膜厚变化可以表示为式（6）。显然，式（5）是式（6）中α=0°和ψ0=0°时的特殊形式。

2 Reynolds 方程及数值计算流程

2.1 水润滑轴承Reynolds方程及边界条件

针对船舶尾轴承的水动力润滑，Reynolds 方程可表示为式（7）：

式中：h为水膜厚度，mm；η为动力黏度，Pa·s；p为流体压力，MPa；ω为轴转速，rad/s；r为轴颈外半径，mm；θ为周向坐标，rad；z为轴向坐标，mm。

取H=h/c、p0=6ηωr2/c2、P=p/p0、λ=2z/L等无量纲参数后，式（7）可转化为式（8）所示的无量纲形式。本文后续中所提到的膜厚及压力分布若无特殊说明，都指无量纲膜厚和无量纲压力。

获得膜厚H的分布后，需要结合压力边界条件才能通过有限差分法对式（8）进行求解。本文采用Reynolds 边界条件，规定水膜厚度最大处为起始点且压力为0；水膜终点在最小膜厚之后的发散区某点，该点同时满足压力和压力梯度为0，如式（9）所示：

通过对水膜压力分布积分，易求得轴承在水平方向合力Fx和垂直方向合力Fy，见式（10）：

2.2 水膜压力数值计算流程

Reynolds 方程的直接计算求解较为困难，通常是采用有限差分法进行数值求解，其计算过程如图4 所示。轴颈倾角、轴承的最大磨损值都是计算之前需确定的输入参数，前者可由轴系校中计算得到，后者根据实际情况确定。

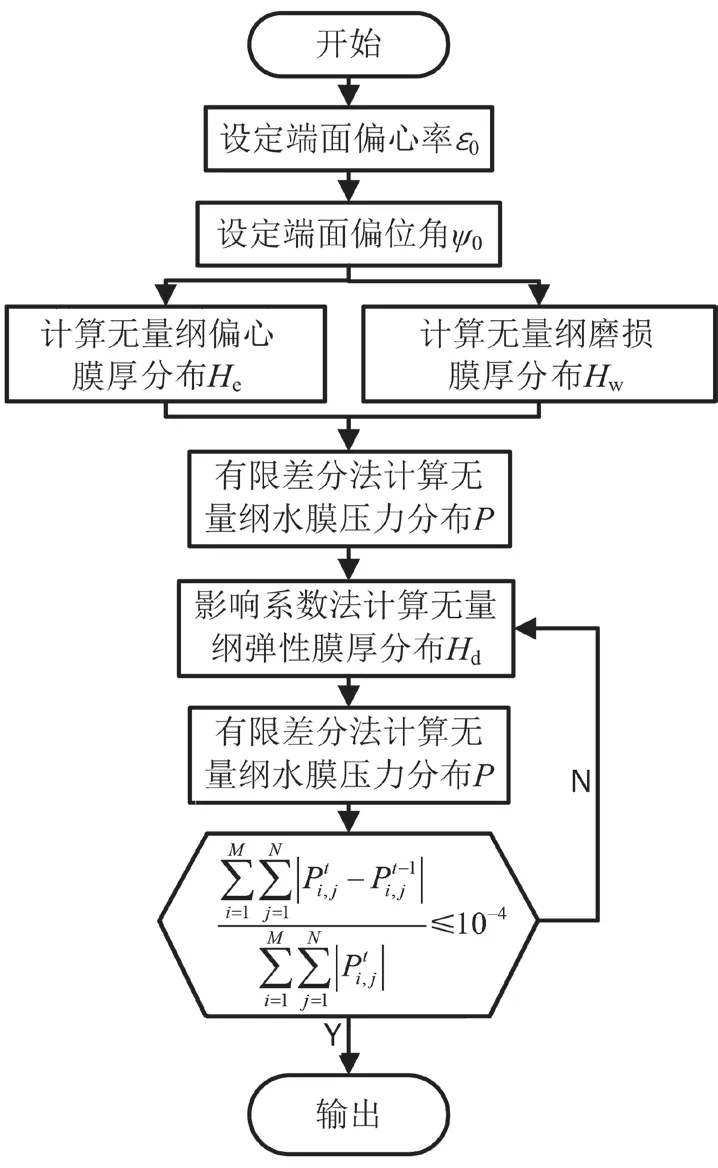
图4 水膜压力数值计算流程

计算时，首先会设定轴承某一端面的无量纲偏心率ε0与偏位角ψ0，求得偏心膜厚分布He和磨损膜厚分布Hw后首次求解压力分布，然后根据影响系数法计算弹性变形对应膜厚分布Hd，将3 种分布叠加后进行迭代计算直至满足误差要求。

船舶尾轴承的负荷实际可通过轴系校中计算获取，而偏心率与偏位角则由于无法测量难以得到。因此需要设置不同的初始偏心率与偏位角值，以使轴承负荷与水膜压力对应的合力相互抵消。

3 结果与讨论

3.1 不考虑倾角与弹性变形时的油膜压力计算

首先，针对文献[8]中存在倾角的油润滑轴承进行计算对比。此时Hd和Hw都为0，相关的参数应与文献[8]中保持一致，计算结果如表1 所示。

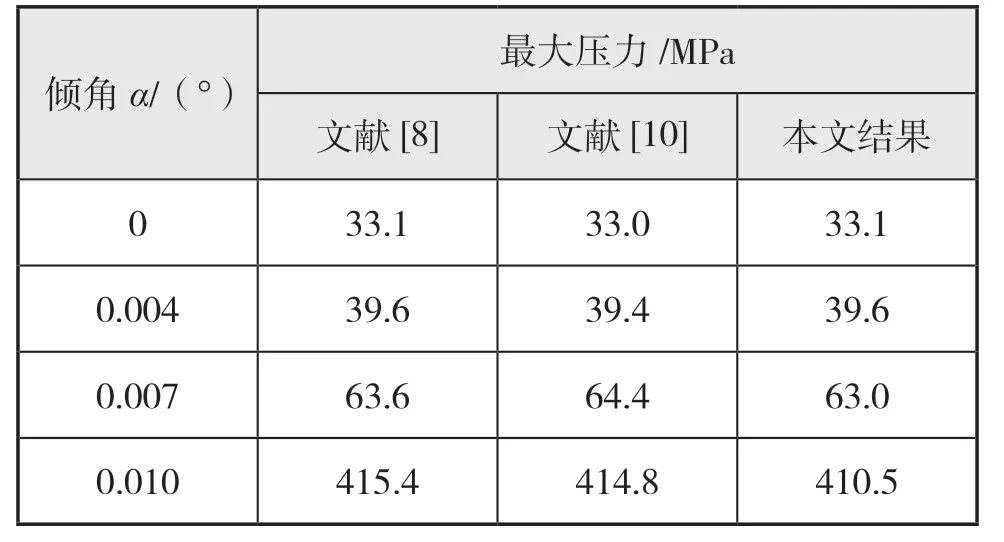
表1 仅考虑倾角时的油膜压力计算对比

可见，计算结果与文献结果接近，由此也验证了本文计算方法的正确性。

3.2 有倾角与磨损时的水膜压力计算

以某船的水润滑赛龙轴承作为研究对象，分析轴承倾角与磨损对水膜压力的影响。轴承相关参数如表2 所示。此表中，安装允许倾角为中国船级社规范[12]的规定值，代表尾轴安装过程中轴颈与轴承的最大允许夹角值；允许磨损厚度则由轴承供应商提供。

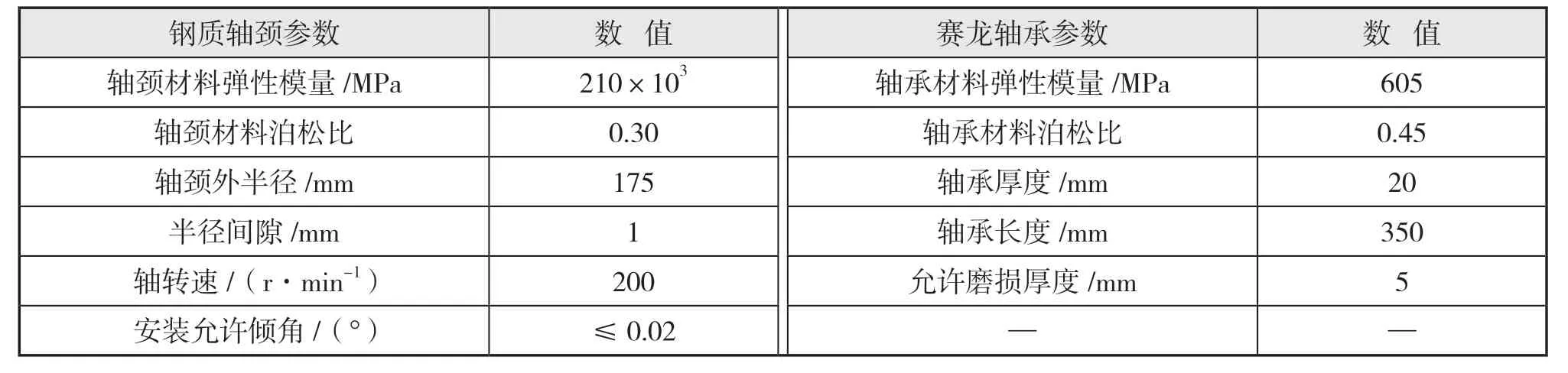
表2 水润滑尾轴承参数表

针对以上轴承，首先假定轴在旋转过程中相对轴承保持固定位置；然后设定最小膜厚相同，首端偏位角ψ0=0°；最后调整倾角磨损搭配，设定3 种不同工况（α=0°、wmax=0 mm，α=0.01°、wmax=0 mm，α=0.01°、wmax=1 mm），经计算便得到如图5 至下页图7 所示的无量纲压力与膜厚分布结果。

图5 偏心率ε0=0.9、ψ0=0°、α=0°、wmax=0 mm 计算结果

从图5 和图6 的对比可以看出：倾角从0°增加到0.01°，水膜最大压力的最大值略微降低，且最大压力点位置向轴承首端偏移。这是因为轴承倾角的存在导致截面偏心率从首端开始沿着轴向逐渐变化。当倾角较小时，从首端到尾端偏心率逐渐减小到最小值；当倾角较大时，从首端到尾端偏心率先减小后增大。一般而言，轴承尾端偏心率值不会大于首端值，因为在船舶尾轴承中，水膜合力主要用来抵消尾轴的重力，方向垂直向上，因此最小偏心率通常都会指向图2 所示坐标系的第2 象限或第3 象限。由此，相同偏心率条件下，存在倾角会使水膜合力下降。

图6 偏心率ε0=0.9、ψ0=0°、α=0.01°、wmax=0 mm 计算结果

图7 所示工况考虑了磨损存在时的情形。可以看到，为保持与无磨损时相同的最小膜厚值，偏心率将大于1。将图7 所示工况与前2 种工况进行比较，可以看出：有磨损时的最大无量纲压力值与无磨损时相近，但都小于无磨损、无倾角时的数值；而压力分布范围从无磨损时的90° ～ 190°变为45° ～ 135°，并且压力由165°左右的较大范围分布变为更靠近122°左右的较窄分布。压力最大值相近，而承压区域减小，说明水膜的承载能力有所降低。结合无量纲水膜分布可发现磨损的存在使最小膜厚位置从180°向122°方向偏移，说明流体楔形入口行程逐渐缩短。对比膜厚分布也容易发现，磨损的存在使膜厚沿着周向变化得更加陡峭。

图7 偏心率ε0=1.9、ψ0=0°、 α=0.01°、wmax=1 mm 计算结果

在实际的使用中，对于轴承间距较大的轴系，尾轴承相对于尾轴的位置姿态会随着船体变形等工况变化而改变，尾轴承所需承担负荷的变化通常较小。因此分析相同负荷条件下具有不同倾角和磨损工况是有意义的。同样以表2 所列轴承进行计算，分析该轴承在额定1 kN 负荷时，内部压力分布随轴承倾角与磨损变化而变化的情况。此时需设置合适的端面偏心率ε0与偏位角ψ0以保证水膜的承载力等于额定负荷，且水平方向合力为0。最大无量纲水膜压力P的计算结果如图8 和图9 所示。

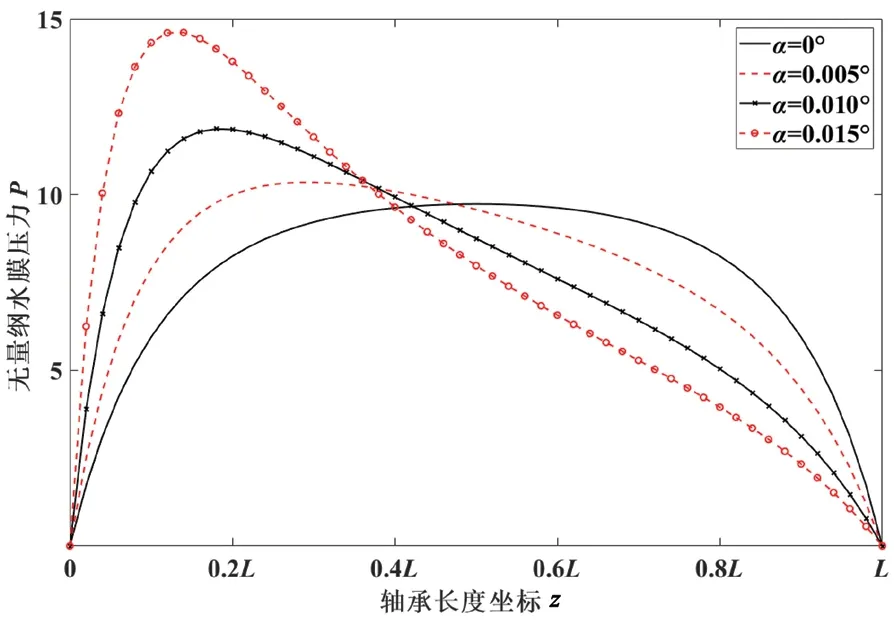
图8 轴承负荷1 kN、wmax=1 mm, 不同α 下压力结果对比

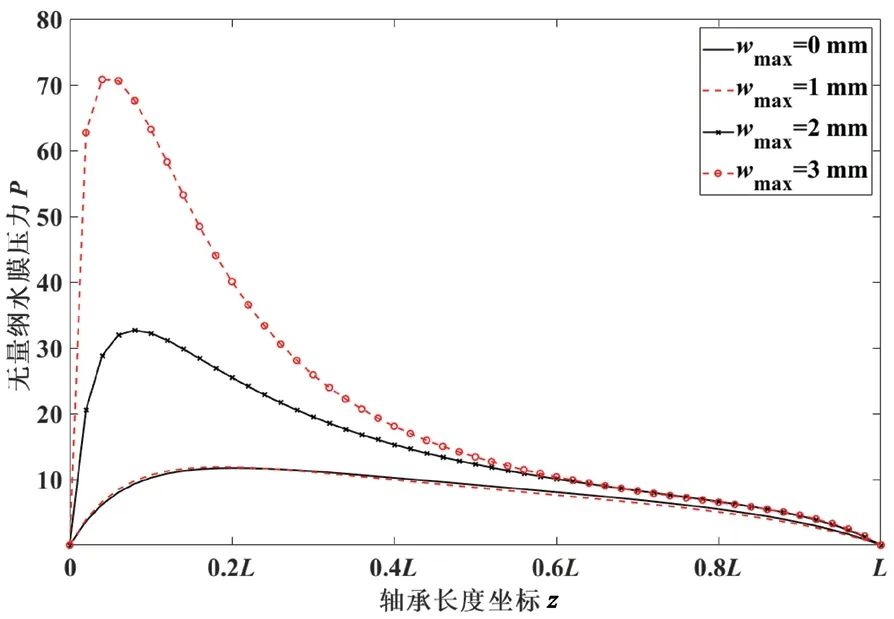
图9 轴承负荷1 kN、α=0.01°, 不同wmax 下压力结果对比

由于不同的倾角和磨损工况对应着不同的端面偏位角ψ0，所以最大压力点的位置各不相同，图中的压力分布都为各工况下最大压力点所对应的轴向沿线。

图8 是最大磨损深度wmax相同但倾角α改变时的压力分布结果对比。可以看出：随着倾角的增加，最大压力逐渐增加，并且其轴向位置逐渐向着轴承首端靠近，轴承首端同时也是磨损较大的一端。倾角从0°增加到0.015°，最大压力增大约1.5 倍。

图9 是倾角α保持不变，最大磨损深度wmax改变时的压力分布结果。可以看出：wmax从0 增至1 mm 的过程中，最大压力值与最大压力位置基本未改变；wmax从1 mm 增加到3 mm 过程中最大压力逐渐增大，其轴向位置向轴承首端靠拢，且3 mm 工况的最大压力相对无磨损时增大约7 倍。从图9 的磨损深度对压力的影响规律可以得出：磨损在一定范围内时，水膜压力分布基本不受磨损的影响；而一旦超过一定值时，水膜最大压力将急剧增加。

由图8 与图9 可见：倾角和磨损的存在都会使最大压力增加，并使最大压力位置点向着首端面移动。这样导致的结果是：首端的水膜压力越来越大，高压区域面积越来越小，尾端的区域逐渐不承压。而水膜压力增大，正对应水膜最小厚度的减小。当水膜最小厚度减小到与摩擦副的表面粗糙度接近时，润滑状态将逐渐向混合润滑和边界润滑转变，此时摩擦系数急剧增大，磨损速度将极大增加。由此，使用理想工况（即无倾角与无磨损的状态）下的轴承磨损速率估算实际使用寿命是不合理的，需要综合考虑因环境工况恶化带来的轴承磨损速率的增大。

4 结 论

综上所述，本文得出主要结论如下：

（1）考虑到水润滑轴承存在倾角与磨损时的情况，给出了相应的水膜厚度计算公式，并引入Reynolds 方程中求解轴承水膜压力分布；通过对无倾角、无磨损情形进行计算对比，验证了计算方法的正确性。

（2）轴承倾角与磨损的存在都会影响水膜厚度分布，导致水膜压力分布的改变；倾角的存在引起的水膜分布是连续变化的，而磨损的存在将导致水膜分布存在阶跃变化点，导致流体楔形区域缩短，使水膜压力分布范围减小。

（3）在相同轴承负荷条件下，随着轴承倾角与轴承磨损的增大，水膜最大压力会逐渐增大。随着倾角增大，压力分布呈连续缓慢地变化；随着磨损深度增大，在一定磨损范围内，压力分布变化很小，超过某磨损值后，压力分布急剧变化。

（4）当轴承倾角与磨损值约为设计规范允许值的一半时，轴承的最大压力相较于理想的无倾角、无磨损情况已增大7 倍；同时，随着倾角与磨损的增大，最大压力点会逐渐向着偏心距最小、磨损最大的端面靠近，表明倾角与磨损的增大会进一步加剧已磨损端的磨损。在估算轴承寿命时，应考虑该加速效应。