基于高阶应变梯度塑性理论的受限薄层剪切问题研究1)

华奋飞 罗 彤 雷 剑,† 刘大彪,†,2)

* (华中科技大学航空航天学院,武汉 430074)

† (湖北省工程结构分析与安全评价重点实验室,武汉 430074)

引言

大量微纳米力学实验表明,当金属材料非均匀塑性变形的特征尺寸处于微米及以下量级时,其呈现出与宏观块体材料截然不同的塑性力学行为,如尺度效应[1-6]、反常包辛格效应[7-10]等.代表性的实验包括微纳米压痕[3]、微扭转[1]、微弯曲[4]和受限薄层剪切[11]等.通过一系列纳米压痕实验,Nix 等[3]发现单晶铜和经过冷加工的多晶铜的硬度和压痕深度上呈现明显的线性关系.Fleck 等[1]在细铜丝扭转与拉伸实验中发现,当丝径从170 μm 降低到12 μm时,无量纲的扭矩增至3 倍,而在拉伸实验中未发现尺度效应.近年来,Dunstan 等[12]和Liu 等[6,13]开展的微尺度金属丝扭转实验也进一步验证了此类现象.Stölken 等[4]对不同厚度的镍薄膜进行了弯曲实验,捕捉到了明显的尺度效应.他们同时对镍薄膜进行了单轴拉伸实验,却没有观察到尺度效应.因此,上述实验中的尺度效应本质上与非均匀变形引起的塑性应变梯度有关.一些非比例加载条件下的微尺度实验[7-10]和离散位错动力学模拟[14-16]表明,在微米或亚微米尺度下,金属材料在非均匀循环变形中会出现“塑性恢复”现象,即反向的塑性流动甚至在卸载时就开始发生.Xiang 等[7]采用鼓膜法对铜薄膜在循环载荷下的力学行为进行了研究,实验结果表明钝化处理后的薄膜在循环载荷作用下出现了“塑性恢复”现象,即反常包辛格效应,但在未钝化的薄膜中没有观察到这类现象.Kiener等[9]研究了循环弯曲加载下单晶薄铜梁的力学行为,实验结果显示铜薄膜在循环弯曲作用下具有强烈的尺度效应,其中包辛格效应随着厚度的减小而愈发显著.类似的现象还出现在循环弯曲[8]、循环扭转[10,17]等非比例加载实验中.然而,在循环拉-压[18-19]等均匀变形中并没有发现尺度效应和包辛格效应.从物理机制来看,非均匀变形诱导的几何必需位错(geometrically necessary dislocations,GNDs)是产生尺度效应和反常包辛格效应的一个重要原因[1,7-8,17,20-22].

传统塑性理论中不包含与材料特征尺度相关的参量,故其无法描述实验中观察到的尺度效应和反常包辛格效应等力学行为.考虑到塑性应变梯度和GNDs 的关系,相关学者构造了应变梯度塑性(strain gradient plasticity,SGP)理论来描述实验中的尺度效应[3,20,23-27].SGP 理论的主要特点是引入了与材料特征长度相关的参量,并且抛弃了经典连续介质力学中的“局部化”假设,而是假设一点的应力不仅与该点的应变(历史)有关,同时也与该点的应变梯度(历史)有关.目前,根据是否引入高阶应力以及相应的高阶边界条件,可以将SGP 理论分为低阶和高阶两种类型.高阶SGP 理论包含高阶应力和高阶边界条件,可以准确预测钝化效应和边界层效应.然而,低阶SGP 理论只考虑了柯西应力项,以位移作为唯一变量,无法解释与边界层相关的应变梯度演变机理[7,28-29].近年来,由于在预测实验现象和处理复杂边界值问题等方面的优势,以Gudmundson 理论[25]为代表的高阶SGP 理论受到广泛关注,并逐渐成为高阶应变梯度塑性理论发展的主流框架.

当材料尺寸接近微观结构的固有尺寸时,材料的界面力学性能和完整性变得尤为关键.理论计算和实验证明钝化层会阻碍位错运动,造成位错堆积,引起材料的应变硬化或强化行为[7,30-31].Mu 等[11]设计了一种开创性的实验方案,对夹在两个硬质陶瓷涂层之间的铜薄层构成的多层结构进行压缩实验.由于铜薄层与微柱中心轴呈45°放置,此时金属层将受到压缩-剪切组合作用.陶瓷作为一种硬质弹性材料,不易发生塑性变形,因此塑性流动在金属与陶瓷界面处受到限制,从而导致塑性应变梯度的出现.实验结果表明,铜薄层的流动应力对铜薄层厚度有很强的依赖性,随着厚度的减小流动应力显著增大.钝化层的出现阻碍了位错的滑移,导致由塑性应变梯度引起的GNDs 在边界处大量堆积.然而,基于传统SGP 理论的预测值显著偏离实验结果[32].Zhang等[33]对陶瓷/金属/陶瓷界面进行了微观分析,发现在界面附近会形成错配位错结构,从而降低结构的剪切强度.Zhang 等[33]指出,在加载的早期阶段,钝化界面出现“锁定”,即此处的塑性应变受到严格约束,可以视塑性应变为0,然后在某一加载阶段发生“解锁”.Kuroda 等[32]采用传统SGP理论对受限薄层剪切问题进行了分析,并给出了材料尺度参数的变化规律.他们认为实验和理论之间的差异并非源自于理论缺陷,而是界面处GNDs 的饱和导致边界条件的改变.

本文基于Gudmundson 高阶SGP 理论,对压缩-剪切组合作用下的受限金属薄层进行有限元分析,研究高阶位移边界条件和压应力对受限金属薄层塑性力学行为的影响.相比于纯剪切情况,压应力的存在能够降低剪切屈服应力,进而解释实验中的尺度效应.考虑界面GNDs 饱和引起的塑性流动局部恢复,我们引入周期性的钝化表面,以揭示微观边界条件在描述金属薄层受限剪切塑性力学行为时的重要作用.

1 高阶应变梯度塑性理论

1.1 本构方程

2004 年,Gudmundson[25]推广了Fleck-Hutchinson 虚功原理[24],采用塑性应变张量代替其中的等效塑性应变,并抛弃了传统的塑性流动一致性假设,提出了一种新的应变梯度塑性理论.Gudmundson 高阶SGP 理论一般适用于小变形、各向同性的情况,并引入微应力来控制塑性流动的方向.该理论假设弹性应变、塑性应变及其梯度都对内部功产生影响.忽略体积力的情况下,虚功原理表示为

式中,ni为外表面S的单位外法向量.

高阶应力 τijk可以分解为耗散项和储能项之和,故有

假设微观应力是完全耗散的[34],则有

考虑到GNDs 的影响,假设自由能 Ψ 仅依赖于弹性应变和塑性应变梯度,即[25]

式中,Cijkl是各向同性弹性刚度张量,G是剪切模量,L是储能尺度参数.由式(6),可以得到柯西应力

储能高阶应力可以推导为

在塑性变形过程中,塑性应变率及其梯度均耗散能量.由于耗散必定是非负的,需要满足以下热力学限制

式中,ℓ 是耗散尺度参数.根据式(9),微观应力和耗散高阶应力的表达式如下

为了规避数值计算和弹塑性边界识别方面的复杂性,这里采用了各向同性的黏塑性本构.广义等效黏塑性流动应力方程表示为

其中流动应力函数 σy(EP) 表示为

1.2 高阶边界条件

采用高阶SGP 理论分析边值问题时,必须规定附加的高阶边界条件.对于弹塑性固体的变形,需要在弹塑性边界和变形体表面施加边界条件.随着加载的进行,塑性区域不断地变化,这就要求塑性应变(或塑性应变率)在弹塑性区域的交界处为0[25].

在变形体表面,一般考虑两种边界条件,自由表面和钝化表面.对于自由表面,其传统和高阶边界条件分别为

式中采用了高阶静态边界条件,也为微观自由边界条件,表示位错可以从表面处自由滑出.

对于钝化表面,其传统和高阶边界条件分别为

式中采用了高阶微观边界条件,也即微观钝化边界条件,表示位错无法穿透钝化表面并发生堆积.

2 高阶SGP 理论的有限元实现及应用

2.1 有限元实现

基于隐式欧拉时间积分方案,本节对包含储能和耗散梯度的Gudmundson 理论进行有限元实现.利用有限元软件ABAQUS 中的用户自定义单元子程序(UEL),构造以位移u和塑性应变 εP为运动学变量的8 节点二次单元,如图1 所示.对于平面应变问题,每个节点包含5 个自由度,即.由于位移和塑性应变均为独立变量,故可通过约束塑性应变来施加钝化边界条件.

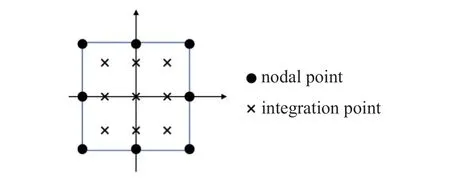
图1 自然坐标系下的二次单元Fig.1 A quadratic element in natural coordinate system

利用上述各式,将内部虚功离散化为

采用Newton-Raphson 迭代算法,为确保算法的2 阶收敛,再令残值R分别对求微分得到一致单元刚度矩阵K,故有

对上述非线性方程组(24)迭代求解,可得到任意时间步 Δt的位移和塑性应变增量.有限元实现的细节可以参考Martínez-Pañeda 等[34]的工作.

2.2 受限剪切问题的有限元模拟

Mu 等[11,36-37]开展了含Cu 薄层的微柱压缩实验,获得了塑性流动应力和试样厚度之间的关系,观察到了明显的尺度效应.如图2 所示,当CrN/Cu/Si微柱受到轴向压缩加载时,对位移矢量分解,45°倾斜的Cu 薄层受到压应力和切应力的组合作用.Mu等[11]发现,SGP 理论可以预测一般的实验趋势,但会高估Cu 薄层的屈服强度.以往研究将该问题理想化为钝化层约束下的纯剪切问题,却忽略了压缩载荷的影响.我们最近的分析表明,附加的压缩载荷可能会导致理论分析和实验结果之间产生差异[31].因此,一维理论模型不再适用,需要二维有限元框架来研究,以避免高估流动切应力[31].

图2 压缩和剪切组合作用下的金属薄层Fig.2 Thin metallic layer under combined compressive and shear loads

考虑具有耗散和储能梯度效应的弹性-刚塑性材料,对宽高比为W/H=4 的薄层进行压缩-剪切加载.该有限元模型中,其厚度方向为20 个单元,宽度方向为80 个单元,单元总数为1600,节点数为5001.上下表面设为钝化边界,即在x2=±H/2 处=0 .左右两侧边界为自由状态,即在x1=±W/2 处Ti=0和tij=0 .在上表面x2=H/2 处施加单调变化的位移u1=-u2=U(t),下表面固定,即在x2=-H/2 处u1=u2=0 .无限大薄层纯剪切问题由于在x1方向上没有应变梯度,实质上可看作一维问题[30].此时仅在厚度上采用20 个单元进行模拟,并在该列单元两侧施加边界条件.

有限元模拟中采用的材料参数见表1.唯象应变梯度塑性理论中材料尺度参量的物理意义尚不清晰,尽管在这方面已经有一些尝试[38-40],但仍未达成共识.为了表征储能梯度和耗散梯度在变形中的作用,文中采用了无量纲处理方式,即采用材料尺度参量和几何尺寸的比值,探究其变化对塑性力学行为的影响.但在与具体实验对比时,会通过与实验数据拟合获得相关参数.

表1 材料参数[41]Table 1 Meterial parameters[41]

3 结果与讨论

3.1 完全钝化边界条件的有限元模拟

本节在Gudmundson 高阶SGP 理论框架下,对Mu 等[11,36-37]的含受限薄层的微柱压缩问题进行有限元模拟,并将数值结果与实验结果进行对比,以强调压缩载荷的重要作用.不同于纯剪切问题,受限剪切薄层会同时受到压缩和剪切的组合作用.因此,二维有限元分析十分必要.这里假设加载过程中受限薄层为完全钝化状态,表面塑性应变一直保持为零.

不同耗散尺度参数 ℓ 和储能尺度参数L下的归一化切应力与应变关系如图3 所示.可以看出,耗散梯度效应显著增加了薄层的剪切屈服强度,而储能梯度效应则显著提高了屈服后的应变硬化率.当材料发生塑性变形时,表现出两种热力学过程,即基于位错机制的储能和耗散过程[42].统计存储位错(statistically stored dislocations,SSDs)和GNDs 结合产生林硬化,进而导致耗散强化,是导致尺度效应的原因.这种观点被Fleck 等[43]所采纳,即采用合适的局部滑移系配置,内界面可以导致耗散强化.GNDs 源于晶界对位错的阻碍或材料的表面钝化,与之相关的位错塞积产生背应力,进而产生储能强化,是产生包辛格效应的原因.这种观点被Gurtin等[20,26,44]和Gudmundson[25]所采纳.对于只考虑耗散梯度效应的算例,屈服切应力随 ℓ/H的增大而提高,塑性阶段的应变硬化没有明显的变化.而对于只考虑储能梯度效应的算例,塑性阶段的应变硬化率随L/H的增大而提升,而屈服切应力不变.当不考虑应变梯度效应时 (ℓ/H=L/H=0),屈服切应力和塑性应变硬化率都较小.在弹性阶段,切应力随u1/H呈线性增加,而后由于压缩载荷的影响,屈服后的流动切应力随u1/H的增加而逐渐减小.对于这种“软化”现象,其原因是薄层在剪切屈服后,持续增加的压应力导致剪切带发生改变.当同时考虑两类梯度效应时 (ℓ/H=L/H=0.5),屈服切应力和应变硬化率都显著增加.

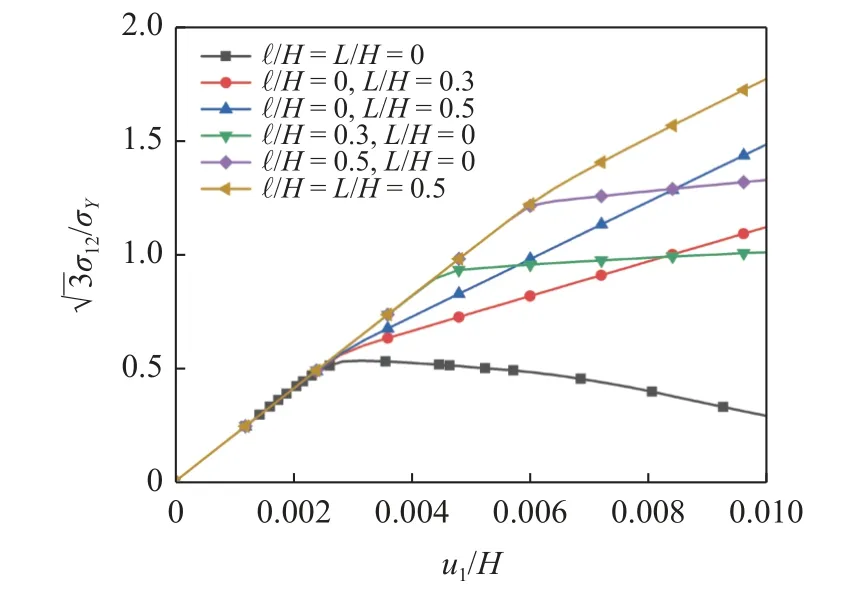
图3 压缩-剪切组合作用下归一化的切应力-位移关系Fig.3 Normalized shear stress-displacement relation under combined compression and shear

分别考虑耗散梯度效应和储能梯度效应作用的塑性切应变 γP沿薄层厚度的分布云图如图4 所示.可以看出,梯度效应是由非均匀变形,以及顶部和底部表面的塑性流动的充分约束引起的.在整个变形过程中,在高度和宽度方向上都存在着强烈的塑性应变梯度.

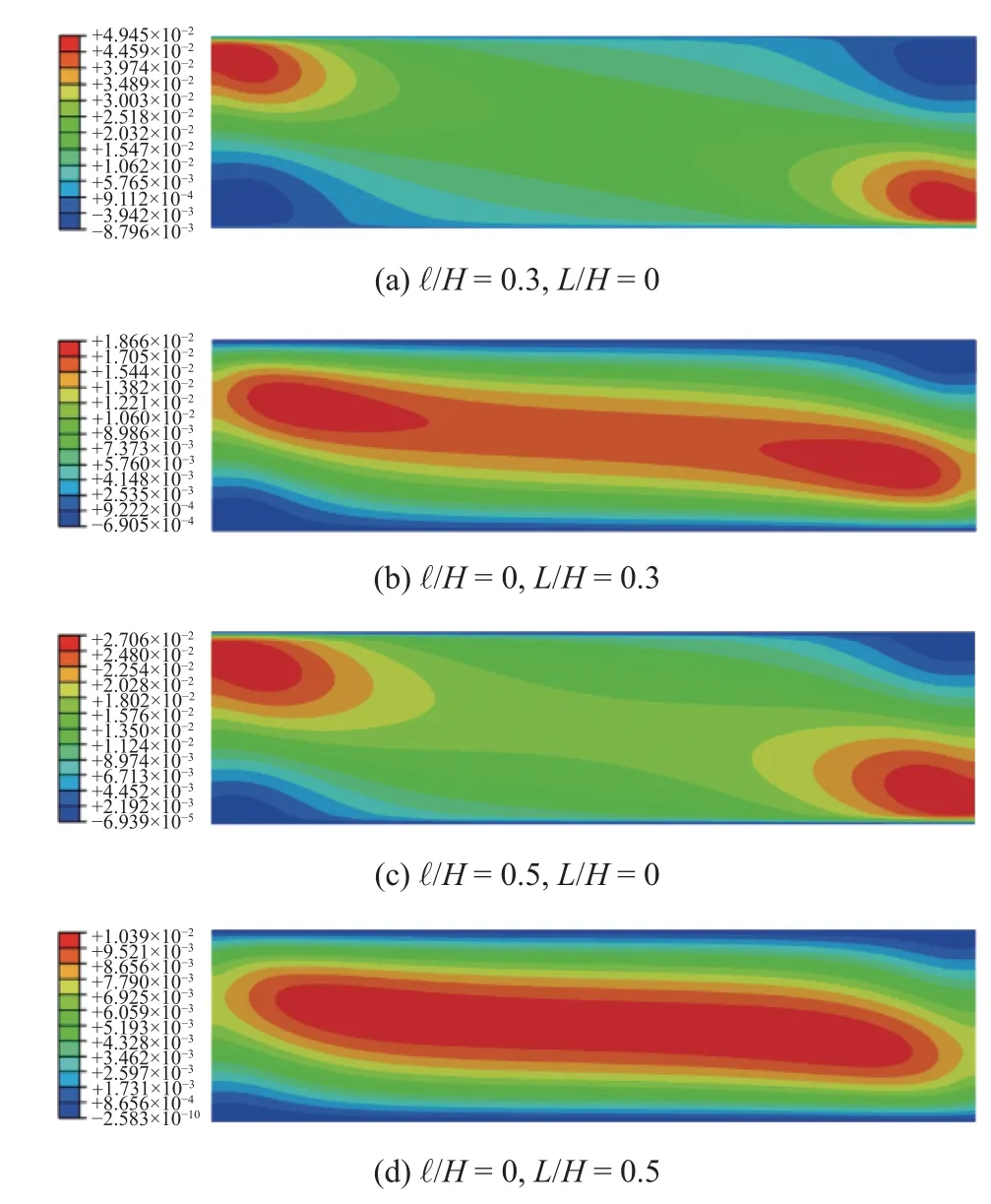
图4 u1/H=0.02 时塑性切应变 γP 的分布云图Fig.4 Contours of the plastic shear strain γP atu1/H=0.02

Gudmundson 理论的数值模拟结果与Mu 等[11]的实验结果之间的对比如图5 所示.同样以实验中约800 nm 厚度的数据为基准进行拟合,材料参数如下: 杨氏模量E=110 GPa,屈服应力 σY=0.35 GPa,泊松比 ν=0.3,硬化指数N=0,耗散尺度参数 ℓ=347 nm .结果表明,基于Gudmundson 理论的有限元结果与实验数据的变化趋势较为接近.然而与Fleck-Hutchinson理论的预测类似,随着金属层厚度的减小,理论值会高于实验值.若没有钝化边界的约束,表面应变梯度效应消失,此时薄层的剪切屈服强度与厚度无关.Zhang 等[33]指出,钝化层在加载过程中对塑性应变的抑制并不是全程严格的,可能会出现“解锁”这种对塑性应变抑制变弱的情况.参考Kuroda 等[32]的方法,我们接下来对受限薄层剪切问题中所施加的钝化边界条件作进一步研究.

图5 SGP 理论预测结果与受限薄层剪切实验结果[11]的比较Fig.5 Comparison between SGP predictions and experimental results of shear deformation of confined layer[11]

3.2 周期变化边界条件的有限元模拟

上述分析证实了压缩载荷会影响剪切流动应力,也有研究指出实验中观察到的过高屈服强度来自于表面边界条件的变化[32-33,45-46].基于SGP 理论的预测与实验的偏差并非由于理论缺陷,而是持续变形过程中界面处GNDs 的饱和导致边界条件发生转变.理论上讲,简单地令塑性应变为0 不足以准确描述此时的边界条件,通常认为存在一个处于自由表面和完全钝化表面的中间态[32].本节主要关注由于界面位错密度饱和诱导边界变化的稳定状态,强调不同类型高阶边界条件的作用.不考虑加载过程中高阶边界条件的突然改变,以及可能带来的非比例加载问题[30,47].本节采用矩形脉冲和正弦两类周期性变化的塑性应变来描述“软-硬”中间态的边界条件.

(1)周期矩阵脉冲信号型边界条件

在薄层的表面上施加如图6 所示的周期矩阵脉冲信号型边界条件,该边界条件的公式表述如下

图6 周期矩形边界条件Fig.6 Periodic rectangular boundary condition

其中 τ=0.5T,P表示钝化边界为激活状态.

周期矩阵脉冲信号型边界条件为

分别取 τ={0,0.25,0.5,1}T进行数值模拟,同时考虑储能和耗散梯度效应,即 ℓ/H=L/H=0.5,计算结果如图7 所示.可以看到,剪切屈服强度和塑性阶段的流动剪切应力都随着 τ 值的增加而增加.实际上,当 τ=0 时,模型退化为表面完全自由的压缩-剪切问题;当 τ=T时,模型为表面完全钝化.可以看到,施加表面周期性钝化能显著降低屈服切应力和流动切应力的大小.

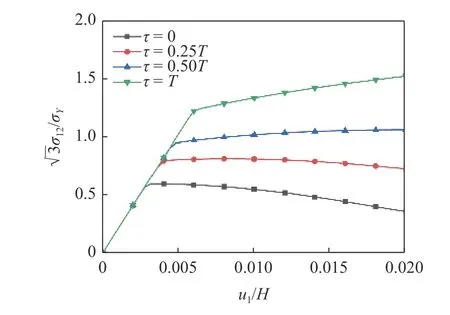
图7 不同周期下归一化切应力与位移的变化关系Fig.7 Normalized shear stress-displacement relation under different periods

不同周期下塑性切应变 γP在薄层内部的分布云图情况如图8 所示.可以明显看到,薄层内的塑性切应变的分布受 τ 的影响.当 τ=0 时,薄层的表面为完全自由状态,对塑性切应变没有任何抑制,此时的塑性切应变主要集中在薄层的角落处.而随着 τ 的不断增大,塑性切应变开始在表面处受到限制,其分布从薄层的角落逐渐往中间部分靠拢.对比图8(d)和图4(d)可以观察到塑性切应变分布相似,其原因在于储能梯度对应变硬化影响更大.因此当同时考虑两个参数时,储能梯度效应占主导作用.此外,图8(d)中考虑了耗散梯度效应,塑性切应变的最大值降低.值得注意的是,在图8(b)和图8(c)中可以明显看出塑性切应变在周期性的表面钝化处受到抑制,同时在周期性的表面自由处得到显著的发展,这种变化趋势符合Zhang 等[33]所描述的表面塑性应变“解锁”现象.

图8 u1/H=0.02 时不同周期下塑性切应变 γP 分布云图Fig.8 Contours of the plastic shear strain γP at u1/H=0.02 under different periods

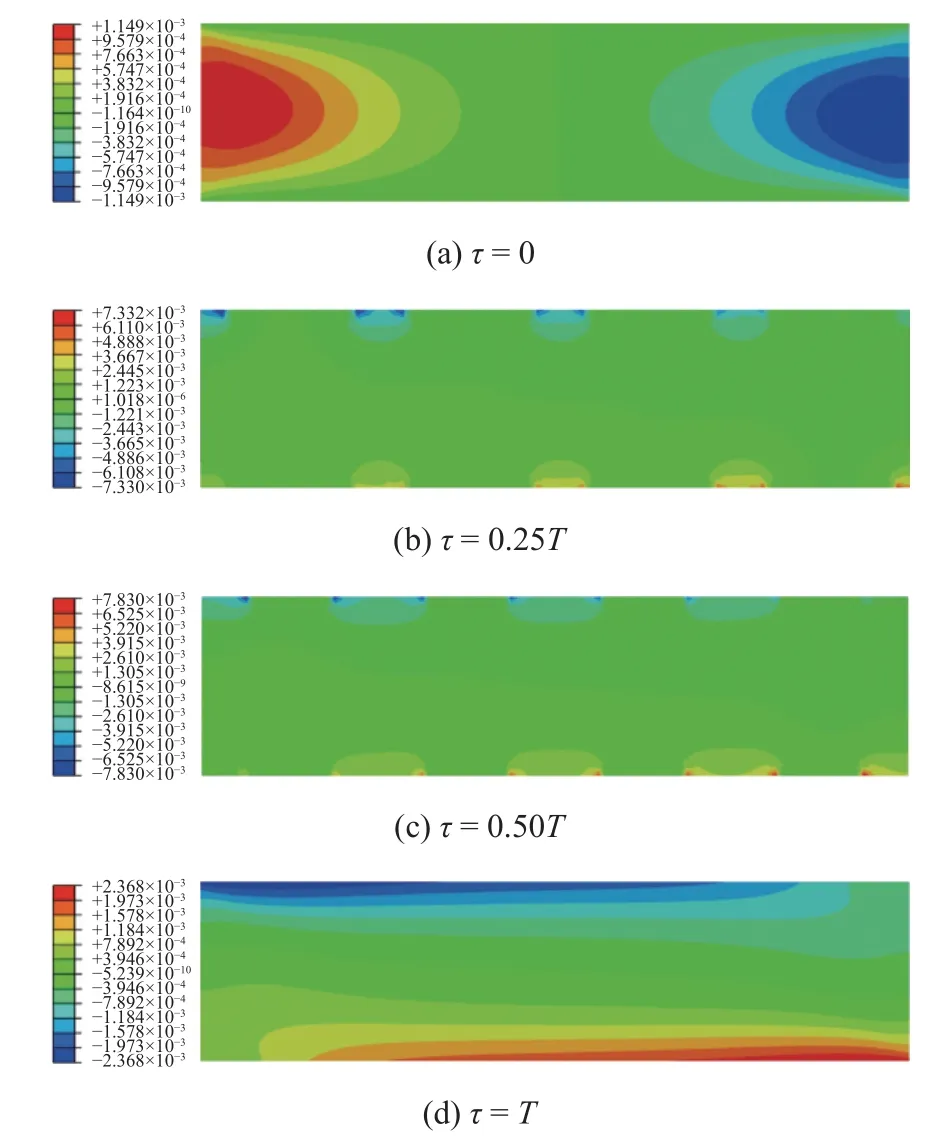
图9 u1/H=0.02 时不同周期下储能高阶应力 分布云图Fig.9 Contours of the higher-order stress at u1/H=0.02 under different periods

(2)周期正弦型边界条件

如图10 所示,若在表面上施加周期正弦型边界条件,塑性应变的变化表示如下

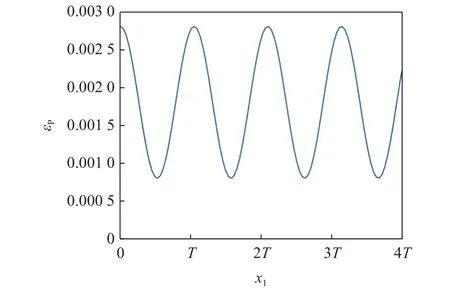
图10 周期正弦边界条件Fig.10 Periodic sinusoidal boundary condition

周期正弦型边界条件为

考虑到收敛性问题,选取A=0.001,B=0.001 8进行相关计算,取 ℓ/H=L/H=0.5,并将结果与完全钝化和自由表面结果进行对比,如图11 所示.可以看出,施加如式(28)所示的表面塑性应变周期性变化的边界条件,显著降低了剪切屈服应力和流动切应力.

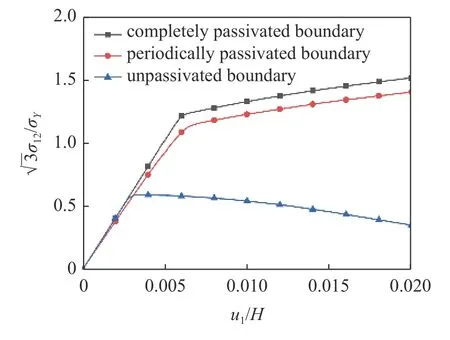
图11 不同边界条件下归一化的切应力-位移关系Fig.11 Normalized shear stress-displacement relation under different boundary conditions

不同表面边界条件下的塑性切应变 γP在薄层内部的云图分布情况如图12 所示.在图12(b)中,可以看到考虑表面塑性应变周期正弦变化的边界条件之后,表面上的塑性切应变明显变得有规律性,而且同时影响了薄层内部的塑性切应变的分布情况.

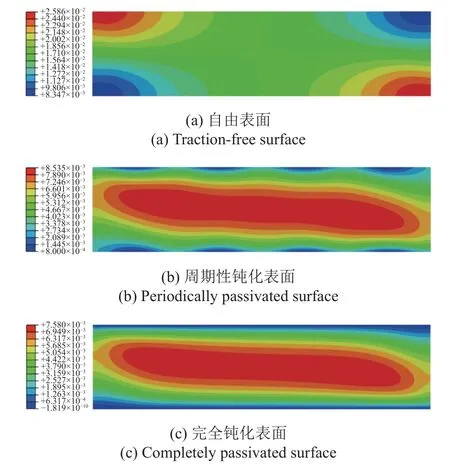
图12 u1/H=0.02 时的塑性切应变 γP 分布云图Fig.12 Contours of the plastic shear strain γP atu1/H=0.02

施加周期正弦型边界条件的有限元结果与Mu等[11]的实验比较如图13 所示.材料参数如下: 杨氏模量E=110 GPa,屈服应力 σY=0.35 GPa,泊松比ν=0.3,硬化指数N=0,耗散尺度参数 ℓ=310 nm .结果表明,当考虑表面塑性应变周期性变化时,基于Gudmundson 理论的有限元模拟结果与实验趋势一致.在加载的早期阶段,钝化界面出现“锁定”,然后在某一加载阶段发生“解锁”.采用表面周期性变化的塑性应变表示“解锁”,可以使理论预测与实验结果趋于一致.当塑性应变梯度达到临界值时,塑性流动局部恢复,边界条件可能发生改变[45].当薄层厚度小于400 nm,实验结果和理论值之间的差异变大,其原因在于材料尺寸和尺度参数接近,导致更强的应变梯度效应[31].

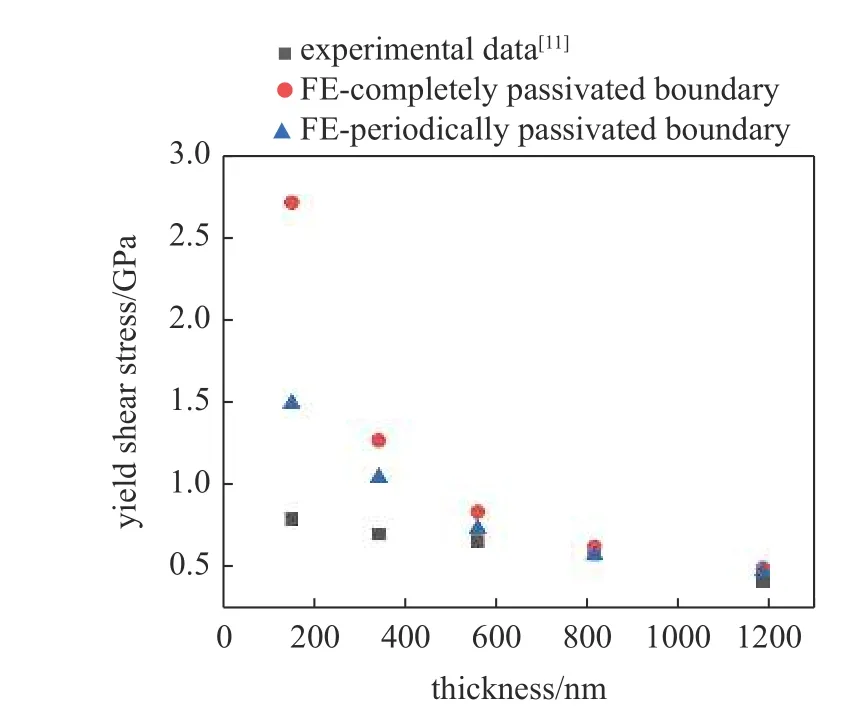
图13 SGP 理论预测结果与受限剪切实验结果[11]的比较Fig.13 Comparison between SGP predictions and experimental results of confined shear[11]

4 总结

本文基于Gudmundson 高阶SGP 理论研究了金属薄层受限剪切问题,定量评估了非均匀塑性变形过程中的储能梯度和耗散梯度效应.构建了含塑性应变自由度的二维有限元框架,有效刻画了钝化边界条件和压应力在金属薄层压缩-剪切组合塑性变形中的关键作用.与纯剪切情形相比,压应力的存在大大降低了流动切应力,从而验证了受限剪切实验中的奇异现象.从位错和界面的相互作用出发,考虑到塑性应变梯度累积引起的高阶应力,导致无法维持零塑性应变的约束并产生局部滑移,我们引入了周期性变化的边界条件.结果表明,采用周期性钝化边界条件能够更好地描述剪切屈服强度的变化趋势,使得理论预测值回归合理水平.该研究揭示了高阶边界条件在微尺度材料塑性变形中的关键作用,为深入理解微结构界面的剪切失效机制提供了理论指导.