基于MFO-VMD 和GMFE 的往复压缩机轴承间隙故障诊断方法

李彦阳，王金东，赵海洋

（1.东北石油大学机械科学与工程学院，黑龙江大庆 163318；2.黑龙江八一农垦大学土木水利学院，黑龙江大庆 163319）

往复压缩机属于典型的石油化工机械，工作环境恶劣，工作强度高，使得往复压缩机中重要零件滑动轴承在工作过程中极易发生故障，造成巨大安全事故，给生产的正常运行带来巨大的经济损失[1-2]。因此，针对往复压缩机建立一套准确的故障诊断方法，可以有效地降低事故发生率。传统的信号分解方法如短时傅里叶变换和小波变换等都存在一定程度上的不足。因此，基于上述存在的问题，DRAGOMIRETSKIY 等[3]在2014年提出了一种新型的信号自适应分解方法—变分模态分解方法（VMD）。VMD 属于一种基于理论基础进行信号分解的方法，具有算法鲁棒性强、各信号分量辨别性高等优点，是处理非线性、非平稳信号的一种理想方法，因此，在各类机械设备故障特征提取过程中被广泛应用和研究，然而VMD 的模态数k 和惩罚因子α 存在着选取困难的问题，从而影响信号分解的效果，因此，对k 和α 进行参数优化成为当前VMD 研究的热点问题[4]。对于VMD 的k 和α 最优参数组合的确定目前常见的方法是采用各类启发式算法进行求解，比如李宏等[5]利用灰狼优化算法搜寻VMD 的最优分解参数组合，并将优化后的VMD 应用于语音信号中进行降噪处理，实验结果表明，该方法实现对语音信号的准确自适应分解。2021 年，张萍等[6]提出了采用鲸鱼优化算法对VMD 的两个关键参数进行优化，以提高对滚动轴承故障振动信号的分解准确率，该算法计算效率快且求解精度高，但易使计算结果陷入局部最优解。基于当前VMD 最佳参数组合确定难的问题以及各类智能寻优算法存在的局限性，本文提出了MFO-VMD 信号分解新方法，以提高信号分解的准确率，降低信号分解重构的误差。

熵值特征提取是机械故障诊断技术中关键的一步，直接影响着故障诊断的结果。近些年来，提出了多种熵值特征提取分析方法，如近似熵[7]、样本熵[8]、模糊熵[9]等，但是随着机械智能化的发展，上述单一尺度的熵值算法无法满足当前复杂机械故障信号的特征提取要求。于是，针对单一尺度熵值算法存在的缺陷，COSTA等[10]提出了多尺度熵，可以更加全面地反映机械故障振动信号的特征信息，为分析时间序列复杂度情况提供了一种新的思路。但是对于多尺度模糊熵（MFE），在多尺度粗粒化过程中，采用的均值粗粒化方式在一定程度上“中和”了原始信号的动力学突变行为，降低了熵值分析的准确性。为了克服MFE 熵值算法存在上述问题，本文提出了一种广义多尺度模糊熵（GMFE），通过利用方差粗粒化代替均值粗粒化进行多尺度处理，使得熵值分析方法更加准确，从而提高故障特征提取的准确性，并将其应用于往复压缩机轴承间隙故障诊断中。

最后，基于往复压缩机内部结构复杂、激励响应众多，本文将建立的MFO-VMD 信号分解方法和GMFE熵值分析方法进行组合，对往复压缩机轴承间隙故障信号进行诊断研究。该诊断方法可以有效地提取故障信号的特征信息，实现轴承故障的准确诊断，对降低事故发生率、提高企业的生产效益具有重要的工程应用价值。

1 变分模态分解方法

VMD 信号自适应分解方法通过构建变分模型的方式对原始信号进行计算求解，将振动信号有效地分解成若干个固有模态分量IMF 的形式，极大地改善EMD存在的端点效应和模态混叠两个固有问题。VMD 对原始信号进行自适应分解的变分模型如下[6]。

式中：｛uk｝表示模态分量的集合；｛ωk｝为对应中心频率的集合；δ（t）表示狄拉克函数；k 为模态数；f 表示振动原始信号；）为经过Hilbert 变换后uk（t）的频谱；∂t表示梯度运算。通过将Lagrange 乘法算子λ 引入式（1）中对VMD的变分模型进行求解，对变分模型中的约束问题进行改进，从而得到增广Lagrange 计算表达式。

式中：α 表示惩罚因子；λ 表示Lagrange 乘法算子。VMD 的具体计算步骤如下所示。

Step3：利用式（4）的判断准则进行终止判别，如果满足停止条件，那么算法运行结束，输出对应的k 个固有模态分量IMF，反之返回至Step2 继续运算。

式中：ε 表示判别精度（ε＞0）。

2 变分模态分解方法的参数优化

由于VMD 中k 和α 的选择会直接影响往复压缩机轴承间隙故障振动信号的分解效果，于是本文利用著名的飞蛾捕焰优化算法（MFO）对VMD 中的关键参数k 和α 进行优化，得到最佳的参数组合［k，α］。

Seyedali Mirjalili 根据飞蛾围绕火焰的整个运动过程，设计了著名的MFO[11]，下面将具体介绍MFO 的原理：

在算法优化过程中，其中式（5）代表着飞蛾在运动过程中空间位置，而式（6）则表示算法的适应度值。在MFO 的整个迭代运行中，飞蛾是根据算法中火焰的适应度值为参考标准来判断是否达到目标函数对应的最优解。

式中：n 表示飞蛾个数；d 表示维度。

对于MFO，需要首先设置火焰的初始值，从而保证与飞蛾的空间位置保持一致。

对于整个飞蛾捕焰的过程，实质为飞蛾围绕火焰做连续的曲线运动并不断更新之前的位置，飞蛾的整个运动过程可以分为两步，第一步是飞蛾向火焰中心方向飞行的过程；第二步是飞蛾由火焰中心向外运动的过程。

2.1 飞蛾捕焰的过程

对于飞蛾捕焰的过程是飞蛾利用其本身的生物特性由外向火焰中心做螺旋运动，并且不断地迭代更新其前一位置，从而逐渐靠近火焰中心，当达到火焰中心位置处，其运动才结束，并且该位置为最佳位置（图1）。

图1 飞蛾围绕火焰的曲线运动图

飞蛾的运动轨迹方程如下所示：

2.2 飞蛾弃焰的过程

飞蛾弃焰的过程是飞蛾随着迭代位置的不断更新，其实火焰的适应度值是需要减去不佳的适应度值，其中具体表示为式（10）所示。

式中：l 表示算法的迭代次数；N 表示算法的最大火焰的个数；T 为最终迭代次数。

在算法的迭代过程中，火焰与迭代次数是成反比关系，并且火焰与飞蛾的初始位置会保证飞蛾的整个寻优过程有效，保证算法的有效性。对于MFO，当适应度函数满足规定要求时，算法则停止运行并输出当前的火焰位置，否则继续向前运行。

VMD 的参数优化过程是首先初置VMD 的两个关键参数k 和α，并计算适应度值，通过利用飞蛾捕焰的过程对两个参数进行不断迭代寻优，直到满足停止条件，则输出对应的参数组合［k，α］，该参数组合则为VMD 的最佳参数组合，然后利用优化后的VMD 对轴承间隙故障振动信号进行分解处理，从而提取轴承间隙的故障特征信息。

3 广义多尺度模糊熵

针对多尺度模糊熵在粗粒化过程中，采用的均值粗粒化方式在一定程度上“中和”了原始信号的动力学突变行为，降低了熵值分析准确性的问题。本文提出了一种广义多尺度模糊熵，通过利用方差粗粒化代替均值粗粒化进行多尺度处理，使得熵值分析的结果更加准确。

假设u=｛ui，i=1，2，3，...，N｝（嵌入维数m、相似容限r）为原始时间序列，采用方差粗粒化计算时间序列的多尺度过程，计算的表达式为：

GMFE 的方差粗粒化见图2。

4 基于MFO-VMD 和GMFE 的往复压缩机轴承间隙故障诊断研究

4.1 往复压缩机轴承间隙故障振动实测信号

本文以往复压缩机轴承间隙故障为研究对象，由于在生产现场进行压缩机故障模拟实验会受到时间、地点等多方面的限制，故本文研究工作采用的实验数据是所在实验室中已有的往复压缩机轴承间隙故障振动信号数据。该数据是由实验室研究人员对大庆某天然气压气站的2D12-70 对动式往复压缩机进行模拟故障实验采集得到的，该实验利用1 号机组已经磨损报废的轴瓦进行不同轴承间隙故障模拟，模拟了一、二级连杆大头轴瓦间隙大，一、二级连杆小头轴瓦间隙大，四种不同位置的轴承间隙故障。此外，也对正常运行的往复压缩机进行测试，获得正常状态的振动数据。其中往复压缩机轴承正常状态、一、二级连杆大头轴瓦间隙大、一、二级连杆小头轴瓦间隙大的振动信号时域图依次见图3[12]。

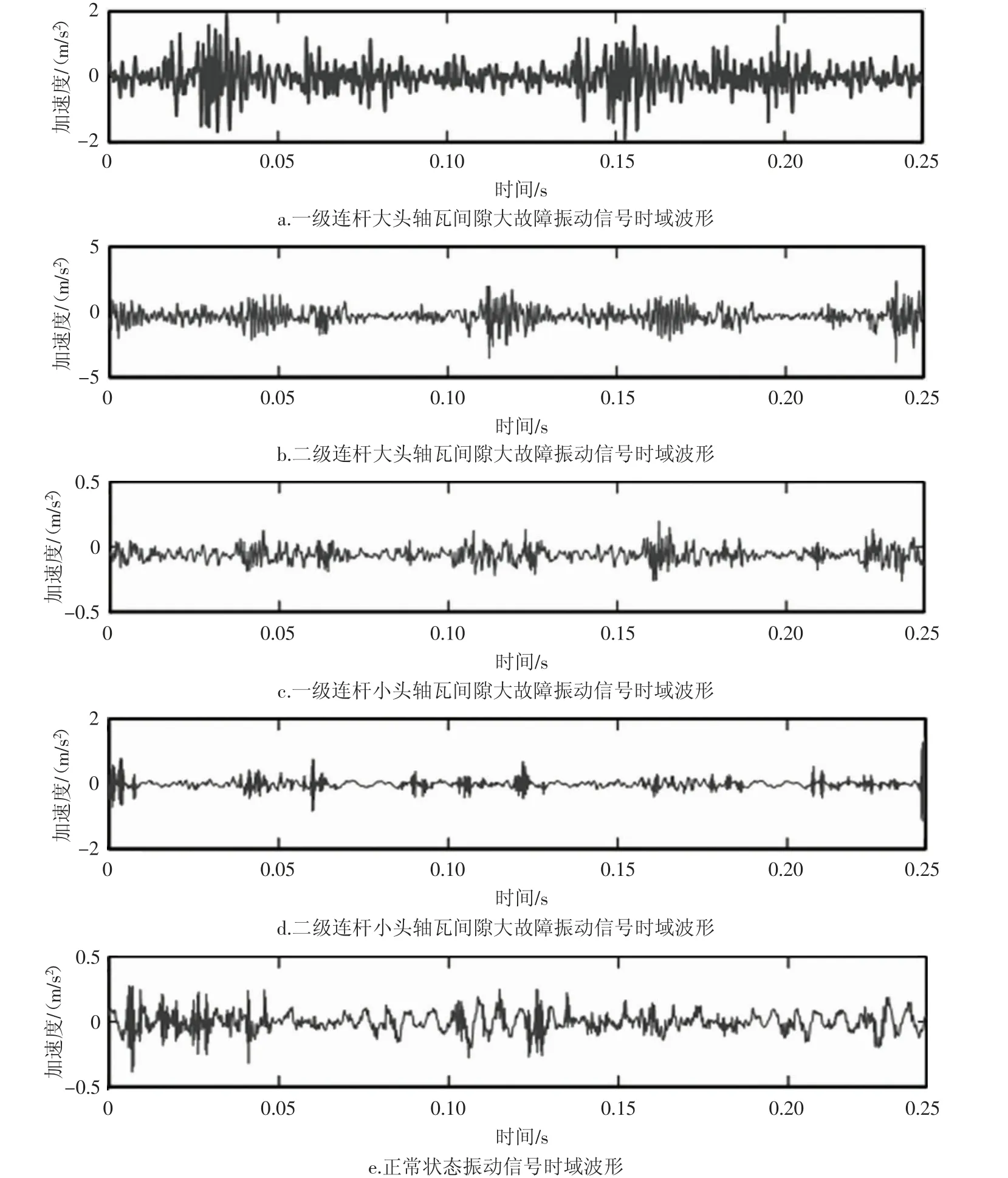
图3 五种不同轴承间隙状态对应的时域波形图

4.2 基于MFO-VMD 的信号分解分析

针对上述五种不同工况轴承间隙振动信号，首先采用MFO 计算VMD 信号分解方法对应往复压缩机五种不同工况轴承间隙振动状态下的最优参数组合［k，α］，由于智能寻优算法在计算过程中具有一定的随机性，因此，采用计算30 次运算结果的平均值作为最终的最优参数组合结果。对应的最优参数组合结果见表1。

表1 最优参数组合［k，α］

将上述计算得到的最优参数组合输入VMD 中，对往复压缩机五种不同工况轴承间隙振动信号进行信号分解，并利用相关性原理对分解后的各IMF 分量进行重构处理。为进一步验证本文提出的MFO-VMD 信号分解方法的优越性，以二级连杆小头轴瓦间隙大状态为例，利用LMD、DE-VMD 和MFO-VMD 三种信号分解方法对往复压缩机五种不同工况轴承间隙振动信号进行信号分解重构处理，然后对重构后的信号进行包络谱图分析，三种信号自适应分解方法对应的重构包络谱图见图4～图6。

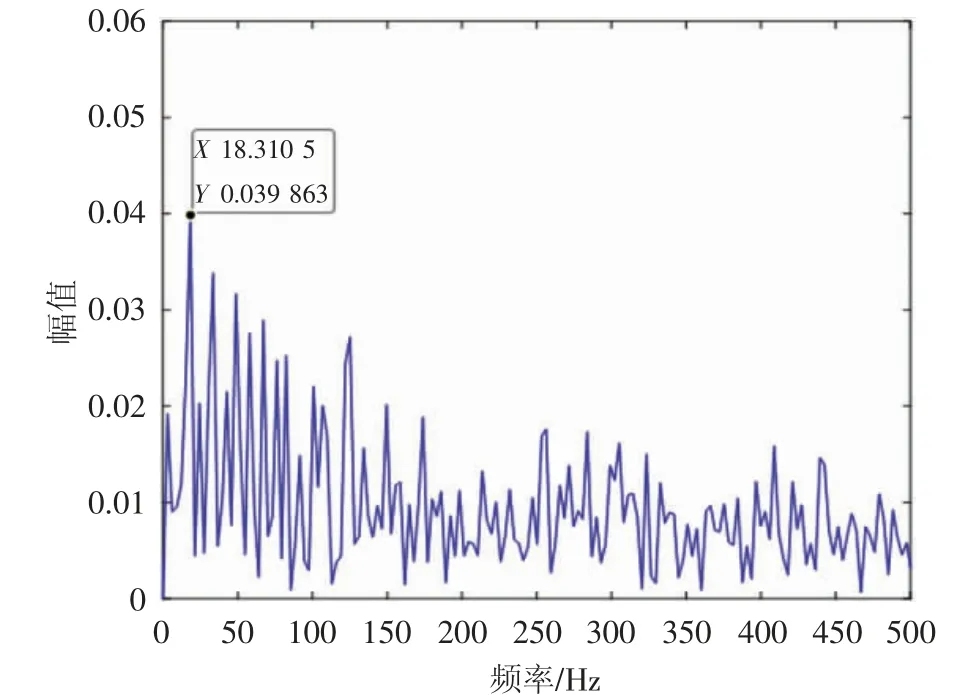
图4 LMD 信号分解重构后的包络谱图

图5 DE-VMD 信号分解重构后的包络谱图

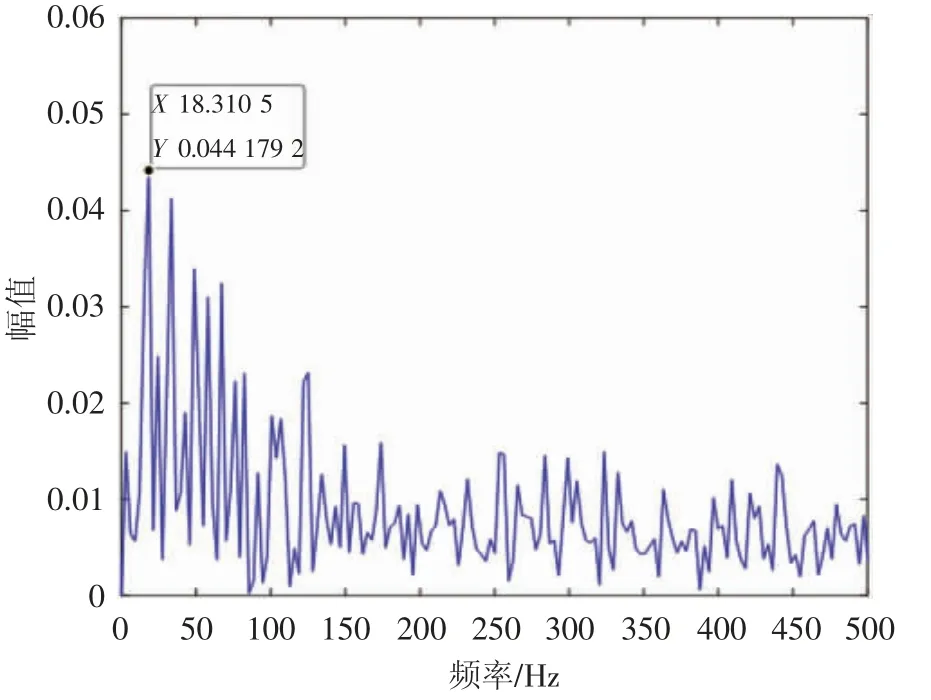
图6 MFO-VMD 信号分解重构后的包络谱图

对比分析图4～图6 可以得出，LMD、DE-VMD 和MFO-VMD 三种信号分解方法重构后的包络谱图均体现了二倍频的峰值，并且与往复压缩机轴承实际故障特征频率保持一致。然而，相比于LMD 和DE-VMD 而言，MFO-VMD 包络谱图中的峰值最大且噪声抑制效果最为明显，因此，较好地验证了本文建立的MFOVMD 信号分解方法的计算优越性，能够更好的对往复压缩机轴承间隙故障进行故障特征提取研究。

4.3 基于GMFE的故障特征提取分析

对上述往复压缩机五种不同工况轴承间隙振动信号进行分解重构处理后，然后利用本文建立的GMFE对上述五种不同工况轴承间隙振动信号分别进行熵值分析，构建轴承间隙的故障特征向量集。其中GMFE 的参数根据参考文献[13]可知，嵌入维数m=2，相似容限r=0.25。为进一步验证GMFE 熵值的优越性，对往复压缩机五种不同工况轴承间隙振动信号分别进行MFE 与GMFE 特征提取对比分析，计算结果见图7、图8。从图7、图8 可以看出，采用MFE 计算的五种不同工况轴承间隙振动信号的熵值曲线在尺度因子大于2 时，熵值随着尺度因子的增加而增加，并且熵值曲线存在着较多交叉重叠，熵值提取效果较差；然而，五种不同工况轴承间隙振动信号的GMFE 表现为随着尺度因子的增加先增加后减少，并且熵值曲线的可分性更好，较好地提取了五种不同工况轴承间隙振动信号的故障特征。对比结果进一步证明了本文建立的GMFE 熵值算法具有更好的熵值特征提取效果。

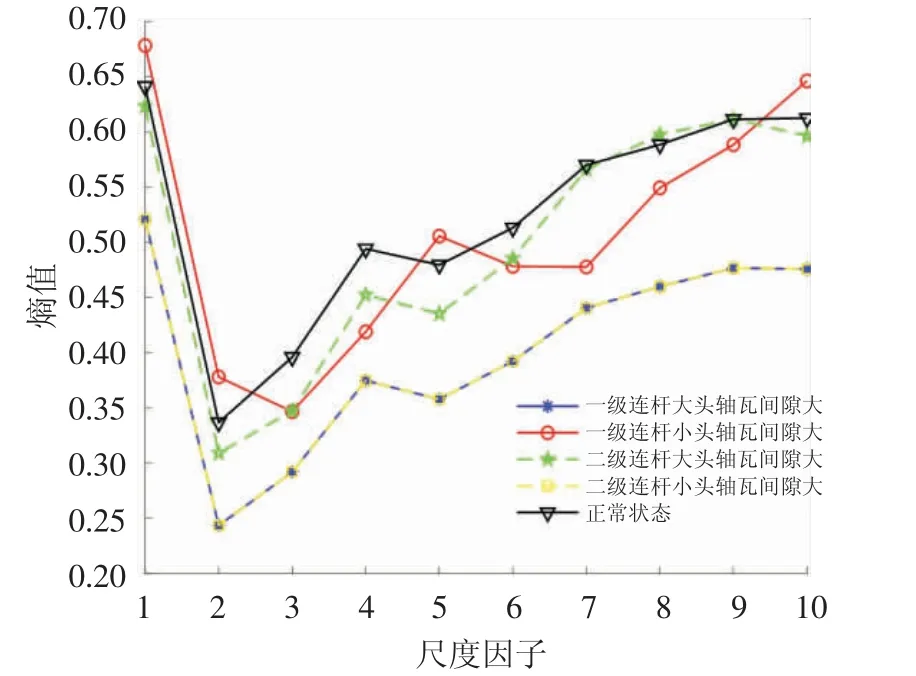
图7 轴承不同工况的MFE 熵值曲线图

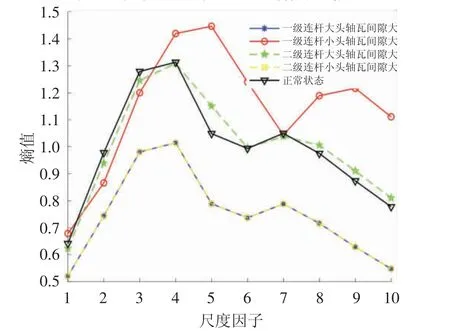
图8 轴承不同工况的GMFE 熵值曲线图

4.4 往复压缩机轴承故障智能识别诊断结果分析

为了验证本文建立的基于MFO-VMD 和GMFE往复压缩机轴承间隙故障诊断方法的有效性和优越性，采用本文方法与其他几种往复压缩机轴承间隙故障诊断方法进行对比分析。首先利用MFO-VMD 对轴承振动信号进行分解重构处理，然后采用GMFE 熵值算法对重构进行故障特征提取研究，最后将提取的故障特征向量集输入到支持向量机（SVM）中进行智能算法的训练和分类研究。

其中提取往复压缩机五种不同工况轴承间隙振动信号的特征向量各210 组，随机选择140 组特征向量作为智能模式识别算法SVM 的训练集，剩余70 组作为识别算法的测试集，从而进行故障的识别诊断研究。往复压缩机轴承间隙的故障诊断结果见表2。分析表2可知，本文构建的基于MFO-VMD 和GMFE 的往复压缩机轴承间隙故障诊断方法准确地实现了不同种类轴承故障的诊断，并且相较于其他几种故障诊断方法具有更好的识别准确率[14-15]。

表2 五种不同工况轴承间隙振动信号的故障诊断结果

5 结论

基于往复压缩机轴承间隙振动信号呈现非线性、非稳定性和特征耦合的特点，本文提出了基于MFOVMD 和GMFE 的往复压缩机轴承间隙故障诊断方法，具体研究结论如下：

（1）提出的面向往复压缩机振动信号局部强非平稳特性的MFO-VMD 信号分解方法，降低了信号分解重构的误差。实验结果表明，与LMD 和DE-VMD 两种信号分解方法相比，MFO-VMD 方法较好地提高了往复压缩机轴承间隙故障的分解准确性。

（2）提出了一种广义多尺度模糊熵（GMFE），通过利用方差粗粒化代替均值粗粒化进行多尺度处理，使得熵值分析方法更加准确，从而提高故障特征提取的准确性。

（3）将提取的故障特征向量集输入到支持向量机中进行识别诊断研究。实验结果表明，本文方法与其他几种故障诊断方法相比，具有更高的总体识别准确率，能够更好地实现不同工况轴承的故障诊断。