A Finite-Time Convergent Analysis of Continuous Action Iterated Dilemma
Zhen Wang , Xiaoyue Jin , Tao Zhang , and Dengxiu Yu
Dear Editor,
In this letter, a finite-time convergent analysis of continuous action iterated dilemma (CAID) is proposed.In traditional evolutionary game theory, the strategy of the player is binary (cooperation or defection), which limits the number of strategies a player can choose from.Meanwhile, there are no effective methods to analyze the convergence and its convergence time in previous works.To solve these problems, we make several innovations in this letter.Firstly, CAID is proposed by enriching the players’ strategies as continuous, which means the player can choose an intermediate state between cooperation and defection.And discount rate is considered to imitate that players cannot learn accurately based on strategic differences.Then,to analyze the convergence of CAID, the Lyapunov function is designed.Furthermore, to analyze the convergence time of CAID, a finite-time convergent analysis based on the Lyapunov function is introduced.In this case, simulation results show the effectiveness of our analysis.
With the rapid development of network science, the evolutionary game theory has been applied in economics, artificial intelligence,and multi-agent systems successfully [1]-[4].Zhanget al.[5] investigate the emergence of oscillatory behavior in evolutionary games that are played using reinforcement learning, providing insights into the evolution of collective behavior.In [6], the evolutionary game theory is utilized to model the evolution process of attacking strategies employed by malicious users, taking into account the dynamics and diversity of these strategies.The driving force mechanism of information is constructed using evolutionary game theory by Xiaoet al.[7] to investigate the factors influencing user behavior during the rumor spreading process.Notably, the strategy of the player is binary or limited in these works, which makes it hard to be consistent with reality.In real-world games, players’ strategies are not limited to full cooperation or full defection.Thus, CAID with continuous strategies of players is proposed in this letter, which means the players can be in an intermediate state of full cooperation and full defection.
Convergence and convergence time are important qualities of evolutionary game theory [8].In [9], the delayed networked evolutionary games model is proposed.Meanwhile, the convergence and evolutionarily stable profiles are analyzed.Maiet al.[10] design a centralized evolutionary game-based pool selection algorithm to analyze the colony behaviors of devices.The convergence in a regular network was analyzed using the Jacobian matrix by Ranjbar-Sahraeiet al.[11].As we can see in these works, the Jacobin matrix is usually introduced to prove the convergence of the evolutionary game,which has a high correlation with the connecting relationship of players.When the relationship between players is very complex, this method cannot be applied.At the same time, it should be noted that the analysis of convergence time has always been hard in the evolutionary game, so proposing a new method to analyze the convergence and convergence time is practical and essential.
In this letter, a finite-time convergent analysis of CAID is proposed.The contributions can be summarized as: 1) To enrich the strategies of players of the evolutionary game, CAID is introduced with continuous strategies.And discount rate is considered to imitate that players cannot learn accurately based on strategic differences.2) The convergence of CAID is analyzed by the Lyapunov function.3) The convergence time of CAID is analyzed by the proposed finitetime convergence method based on the Lyapunov function.Finally,the proposed method is demonstrated through simulation examples using the continuous action iterated prisoner’s dilemma (CAIPD) and continuous action iterated snowdrift dilemma (CAISD), showing its effectiveness.

Thus, one can conclude the difference ΔF jibetween the fitness of playeriandjas follows:
Similar to (5), the dynamic model of strategy adaptation inN-players CAID is
However, in the dynamic model (8), players can learn accurately based on strategic differences, which is not in line with actual games.Thus, we propose a new CAID dynamics model (9) in which player learning exists with a discount rate 0 <α <1
where
Main results: To analyze the convergence of (9), some lemmas are introduced firstly.
Lemma 1 [17]: Suppose that functionV(t) is differentiable such that
坚持治河为民 促进人水和谐 推动治黄事业全面协调发展…………………………………………………… 陈小江(24.68)
whereK>0 and 0 <q<1.Then,V(t) will reach zero at finite timet∗as
andV(t)=0 for allt≥t∗.
Lemma 2 [20]: For a connected graphGthat is undirected, the following well-known property holds:
whereLis the Laplacian of graphGand λ2(L) is the second smallest eigenvalue ofL.
Lemma 3 [17]: Let Υ1,Υ2,...,Υn≥0 and let 0 <p<1.Then,
Theorem 1: If the connecting relationship of players is fully connected, then the dynamic model (9) is finite-time convergent.
Proof: Set
and it can be concluded thatγis invariant becauseaccording to (9).Define the error asei=xi(t)-γ.we can get
Meanwhile, as forγis invariant, we can gete˙i=x˙i-γ˙=x˙i.
Take the Lyapunov function as
Then, it can be obtained that

Then, based on the Lemma 1, the system can realize finite-time convergence.■
Simulation examples: The prisoner’s dilemma is a classic example of an evolutionary game that illustrates how individual rationality can conflict with group rationality.CAIPD is introduced here as an example.The payoff matrix can be described as
wheremdenotes the benefit gained by the individual andkdenotes the price paid by the cooperator, and the parameters satisfym>k.
Snowdrift dilemma is another classic evolutionary game.We also introduce CAISD here.The payoff matrix is
wherem>k.
Setm=5,k=1, β=1, ϵ=0.5 and α=0.5, the simulation results in Fig.1 show the convergence of the CAIPD and CAISD in the full connected network.
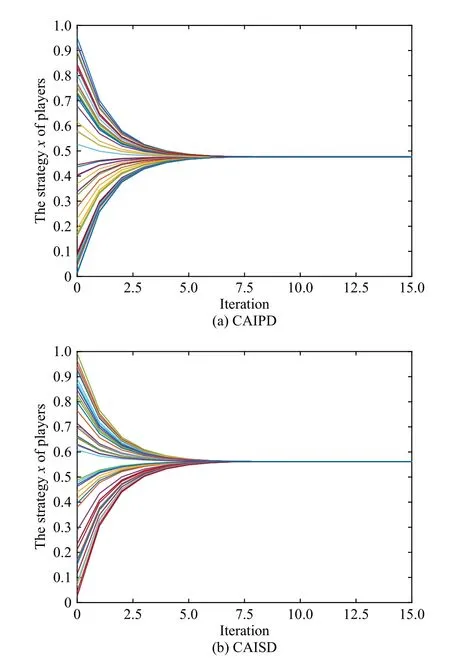
Fig.1.The convergence simulation results of CAIPD and CAISD.
Conclusion: This letter has proposed a finite-time analysis of CAID, which provide a method to analyze the convergence and convergence time of CAID.Firstly, the CAID with continuous strategies has been designed to enrich the binary or limited strategies in traditional evolutionary game theory.And discount rate is considered to imitate that players cannot learn accurately based on strategic differences.Then, the finite-time analysis based on the Lyapunov function has been proposed to avoid the influence caused by the complex connecting relationship of players.Furthermore, CAIPD and CAISD have been introduced as examples to demonstrate the effectiveness of the proposed method.
Acknowledgments: This work was supported in part by the National Science Fund for Distinguished Young Scholarship of China (62025602), the National Natural Science Foundation of China(11931915, U22B2036), Fok Ying-Tong Education Foundationm China (171105), Technological lmnovation Team of Shaanxi Province (2020TD013), and the Tencent Foundation and XPLORER PRIZE.
 IEEE/CAA Journal of Automatica Sinica2024年2期
IEEE/CAA Journal of Automatica Sinica2024年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Reinforcement Learning in Process Industries:Review and Perspective
- Communication Resource-Efficient Vehicle Platooning Control With Various Spacing Policies
- Virtual Power Plants for Grid Resilience: A Concise Overview of Research and Applications
- Equilibrium Strategy of the Pursuit-Evasion Game in Three-Dimensional Space
- Robust Distributed Model Predictive Control for Formation Tracking of Nonholonomic Vehicles
- Stabilization With Prescribed Instant via Lyapunov Method
