Equilibrium Strategy of the Pursuit-Evasion Game in Three-Dimensional Space

Nuo Chen , Linjing Li , and Wenji Mao

Abstract—The pursuit-evasion game models the strategic interaction among players, attracting attention in many realistic scenarios, such as missile guidance, unmanned aerial vehicles, and target defense.Existing studies mainly concentrate on the cooperative pursuit of multiple players in two-dimensional pursuit-evasion games.However, these approaches can hardly be applied to practical situations where players usually move in three-dimensional space with a three-degree-of-freedom control.In this paper,we make the first attempt to investigate the equilibrium strategy of the realistic pursuit-evasion game, in which the pursuer follows a three-degree-of-freedom control, and the evader moves freely.First, we describe the pursuer’s three-degree-of-freedom control and the evader’s relative coordinate.We then rigorously derive the equilibrium strategy by solving the retrogressive path equation according to the Hamilton-Jacobi-Bellman-Isaacs(HJBI) method, which divides the pursuit-evasion process into the navigation and acceleration phases.Besides, we analyze the maximum allowable speed for the pursuer to capture the evader successfully and provide the strategy with which the evader can escape when the pursuer’s speed exceeds the threshold.We further conduct comparison tests with various unilateral deviations to verify that the proposed strategy forms a Nash equilibrium.

I.INTRODUCTION

THE pursuit-evasion game models the strategic interaction among players with conflict goals, whose dynamics over time are depicted by differential equations [1].While the pursuer (P) aims to minimize the time for capturing its opponent,the evader (E) attempts to maximize the capture time.The critical issue in the pursuit-evasion game is to derive the equilibrium strategy for the pursuer and the evader, from which the players can not deviate profitably [2].As the pursuit-evasion game describes the unified strategic target of robots, missiles, and aircraft, it has attracted increasing attention in research and application domains, such as robot control [3],missile guidance [4]-[6], unmanned aerial vehicle (UAV)[7]-[9] and target defense [10]-[12].

Based on the Hamilton-Jacobi-Bellman-Isaacs (HJBI) equation [13], Isaacs proposed the pioneering work of the pursuitevasion game with one pursuer and one evader.Reference[13] utilizes Cauchy characteristics [14] to retrogressively solve the HJBI equation, which starts at all possible terminal states, aiming to derive the equilibrium strategy for arbitrary initial states.The HJBI equation is also applicable for simple multi-player scenarios with two pursuers [15] or two evaders[16].With the increasing demand for pursuit-evasion games with multiple pursuers [17], the relay pursuit strategy based on Voronoi diagrams [18], [19] has been developed to overcome the computational complexity of the original retrogressive method.This strategy assigns one active pursuer to approach the evader while others stay, resulting in limited cooperation among pursuers.

Through a cooperative strategy, the pursuers can effectively encircle a faster evader to ensure capture [20].For a simple case wherePandEmove freely in two-dimensional space with a constant speed, the Apollonius circle [21] is used to describe the cooperative strategy explicitly.This strategy consists of an encirclement phase and an approaching phase [22],in which the success rate highly relates to the included angle[20], [23].Although the Apollonius circle can be generalized to multi-pursuer multi-evader scenarios with optimal alignments [24], it is workable only when players follow the oversimplified assumption on the kinematics ofPandE.Therefore, it can not be employed directly to handle problems in more complex but practical settings, such as three-dimensional pursuit-evasion games, partially observable players[25], and homicidal chauffeur games with complicated control [26].

Recently, researchers have employed multi-agent reinforcement learning (MARL) to learn players’ policies in pursuitevasion games from interacting with the environment [27],addressing more complex issues.Bilgin and Kadioglu-Urtis[17] usedQ-learning to learn the pursuit strategy, which firstly formulates the pursuit-evasion game as a reinforcement learning problem.Later, the minimaxQ-Learning is utilized to iteratively approximate the minimaxQ-function for multiple players [28].With the rapid growth of the actor-critic paradigm [29], algorithms based on deep policy gradient [30],[31] have been proposed to learn policies for the pursuers and evaders.For large-scale pursuit-evasion games, mean-fieldrelated approaches are designed to tackle the challenge caused by complex interactions among players [32].However, the existing MARL algorithms for pursuit-evasion games mainly depend on model-free methods [33], neglecting the deterministic information from player’s kinematics.Besides, the pursuer can hardly capture the evader through initial explorations,which hinders the sampling efficiency during trial-and-error in MARL algorithms.

Therefore, due to the oversimplified problem settings, sampling efficiency, and computational complexity, existing pursuit-evasion algorithms can hardly be applied directly to realworld scenarios wherePandEmove in three-dimensional(3D) space [34]-[36].On the other hand, previous research on three-dimensional pursuit-evasion games tackle the challenge by designing the maneuvering strategies with strictly restricted kinematics, including bounded curvature [37], bang-bang control leaping from the maximum speed to the minimum[38], flight in a vertical plane [39], and one-sided optimal aircraft strategy against a fixed missile [40].However, in realistic scenarios such as air combat and missile guidance, UAVs and missiles commonly follow a three-degree-of-freedom control, in which velocity, pitch angle, and yaw angle construct the player’s control [41].

The equilibrium strategy of the pursuit-evasion game in realistic scenarios remains a versatile but challenging problem.First, the realistic scenario, including dogfights, air combats, and UAVs, requires the player to move in three-dimensional space, controlled by a three-degree-of-freedom model.Besides, the proposed Nash equilibrium strategy is required to reach the saddle point of capture time, and any deviation from the equilibrium strategy will be punished.Furthermore, the proposed algorithm should support real-time decisions for the players in practice.

In this paper, we make the first attempt to theoretically investigate the equilibrium strategy for the players conducting realistic motions in three-dimensional space.We aim to derive the equilibrium strategy for the pursuer and the evader in the three-dimensional region with the HJBI equation.A threedegree-of-freedom control restrictsP’s kinematics whileEmoves at a constant speed without constraint.After constructing relative coordinates with respect toP, the pursuit-evasion process can be partitioned into the Navigation and Acceleration phases according to the HJBI method.Furthermore, we discuss the condition for success capture in detail and provide an escape strategy whenPviolates this condition.

The contributions of our work can be summarized as follows.First, we derive the equilibrium strategy to tackle the realistic pursuit-evasion game by modeling the three-degreeof-freedom kinematics of the pursuer, which is typical in robotics, UAVs, and defense systems.Second, we provide the theoretical derivation of the equilibrium strategy based on the HJBI equation to ensure the minimax property of the equilibrium strategy.Comparison tests further verify that deviations from the proposed strategy perform worse than the equilibrium.Third, we analyze the velocity threshold for a successful capture and then derive the optimal acceleration scheme for the pursuer and the escape strategy for the evader whenever the pursuer’s speed exceeds the threshold.As the proposed strategy can be calculated immediately, our solution of the HJBI equation supports real-time decisions for air combats and missile guidance.

The remainder of this paper is organized as follows.Section II revisits some fundamental concepts and solving methods of differential games, and then formulates the threedimensional pursuit-evasion game.Section III derives the equilibrium strategy for the pursuer and the evader with a rigorous theoretical analysis.Section IV conducts seven experiments to verify that the proposed strategy is the Nash equilibrium.Finally, in Section V, we conclude and raise some future work.

II.PRELIMINARIES AND PROBLEM FORMULATION

In this section, we introduce the fundamental concepts of differential games, pursuit-evasion games, and the HJBI equation.We then describe the pursuer’s three-degree-of-freedom control and the evader’s relative coordinate according to the pursuer.Table I summarizes the notations used in this paper.

TABLE I NOTATIONS USED IN THIS PAPER

A. Pursuit-Evasion Game

A pursuit-evasion game (P,E;x,f(·);φ,ψ;J) follows the framework of differential game, which investigates the equilibrium strategy of players in continuous-time systems [42].A system of differential equations depicts the transition of state variablesx=(x1,...,xn)∈Rn[43]

wheref=(f1,...,fn) denotes the system kinematics, φ(·) andψ(·)denote the control adopted by the opponent players,respectively.In a pursuit-evasion game, the player with control φ is called pursuer, and the player with controlψis called evader.The pursuer aims to minimize the cost functionalJ(x,φ,ψ)while the evader attempts to maximize it [44], which leads to the Nash equilibrium of the pursuit-evasion game

whereTdenotes the time when the game terminates,G(·)denotes the instantaneous reward rate, andH(·) denotes the terminal reward at timet=T.In particular, a conflicting goal in pursuit-evasion games is the capture timeT, equivalent toG=1 andH=0 in (2).Although the time of termination is unknown, the set of terminal statesx(T) as an (n-1)-dimensional manifold is given.

LetV(x) denote the cost functional originating from statexwhenPandEfollow the equilibrium path, i.e., the saddle point ofJ(x,φ,ψ).In the perspective of Bellman’s dynamic programming [45], a pursuit-evasion game can be formulated as a sequence of similar models regarding the statex, in which the transition of states builds the connection between adjacent statesx(t) andx(t+δt)

According to the first-order Taylor expansion concerning timet, we have

where 〈·,·〉 denotes the inner product,denotes the gradient ofV(x), andf(x,φ,ψ)=x˙ is the system kinematics given by (1).Similarly, according to the first-order Taylor expansion, we have

Combining (4), (5) with (3), we derive

By eliminating the infinitesimal time interval δt＞0, we finally derive the following HJBI equation:

As the adjacent time step (t,t+δt) is arbitrarily chosen, the HJBI (7) provides a necessary condition for the equilibrium strategy satisfied at any timet.To solve this first-order partial differential (7), we can convert it into a system of ordinary differential equations according to Cauchy characteristics[14].By taking the partial derivative w.r.t.xk(k=1,2,...,n)on both sides of (7), we have

Equation (10) converts the original (7) into ordinary differential equations onVk.As the set of terminal statesx(T) is known instead of initial states, we retrogressively solve this problem with the inverse time τ=T-t, such that the terminal states are regarded as the initial conditions of differential equations.Combining (10) and the system kinematics (1), we have the following retrogressive path equations (RPE):

Algorithm 1 The Overall Process of the HJBI Method Input: Set of terminal states , system kinematics.x(s) f¯φ, ¯ψ Output: The equilibrium strategy.1: Derive the HJBI equation according to (7).2: Derive the RPE according to (11).V1(s),...,Vn(s)3: Solve the initial condition based on (12) and the HJBI equation.xk, Vk k=1,...,n¯φ, ¯ψ 4: Solve for with the corresponding equilibrium strategy based on (11).¯φ(x) ¯ψ(x)5: return The equilibrium strategy and.

B. Problem Formulation

This paper focuses on the following one-pursuer one-evader game in 3D space, abstracted from a wide range of air combats and UAV practices [35].The pursuer follows a threedegree-of-freedom control while the evader moves freely with a normalized speed ‖vE‖=1.

1)Pursuer’s Control and Kinematics:P’s control variables φ1, φ2and φ3act on the acceleration, yaw angle, and pitch angle, respectively.Fig.1 illustratesP’s movement controlled by φ1, φ2and φ3, where the polar coordinate ofP’s speed isv=(vcosγPcosθP,vcosγPsinθP,vsinγP).Suppose thatP’s initial speed is greater than 0.Regardless of gravity and other resistances, the kinematic equations ofPare

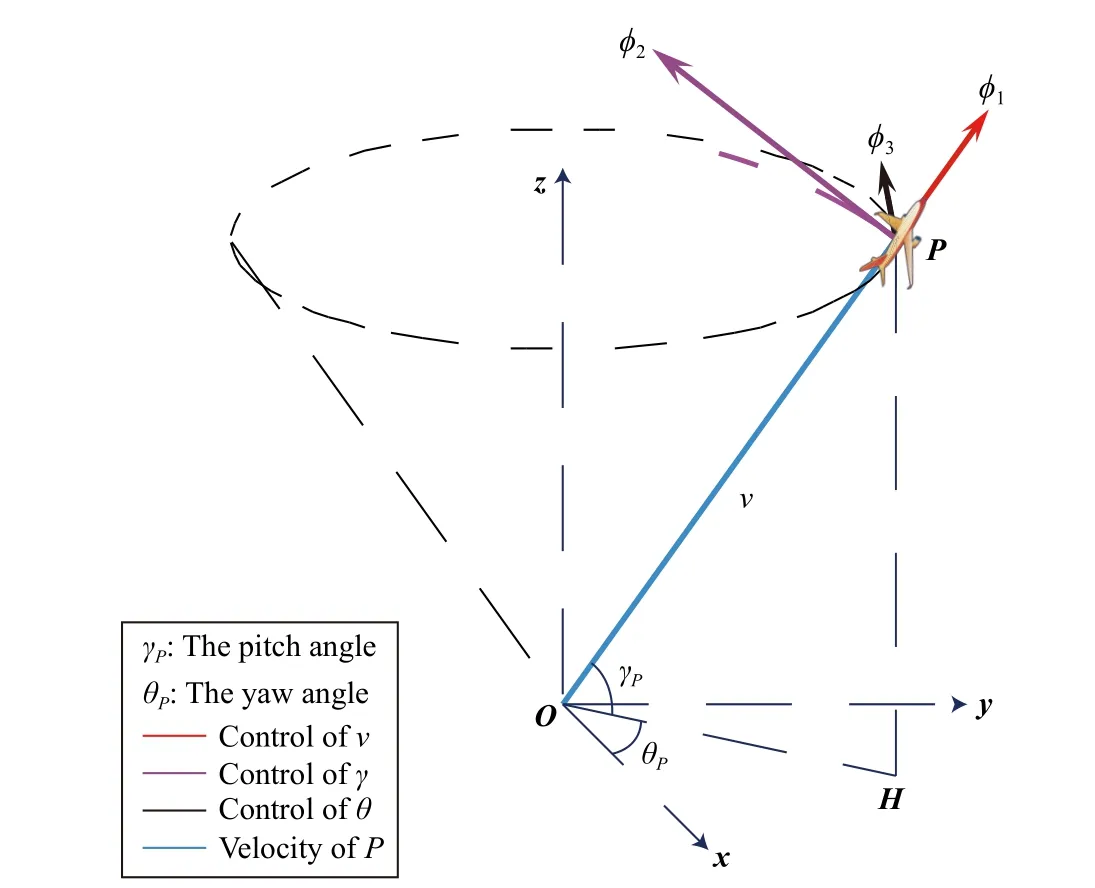
Fig.1.The kinematics of P following a three-degree-of-freedom control.

This three-degree-of-freedom kinematic model (13) is an abstraction of various objects, such as missiles, UAVs, and airplanes [7].

2)Evader’s Relative Coordinate: To representE’s relative position according toP, we define the relative coordinate systemP-xyzoriginating atP, wherexPyis the horizontal plane with an arbitrarily predefinedx-axis, andzis the vertical axis.E’s relative coordinate is (x,y,z) in theP-xyzcoordinate system, and (rcosγEcosθE,rcosγEsinθE,rsinγE) in the polar coordinate system.

According toE’s relative coordinate (x,y,z) andP’s speed(vcosγPcosθP,vcosγPsinθP,vsinγP),E’s kinematic equations are

We first investigateE’s kinematics under the polar coordinate system, in whichE’s state variables are (r,θE,γE) instead of (x,y,z).

Proposition 1: The derivatives of θE, γEandrare

Similarly, we can directly obtain the derivative of γEandr

As shown in Fig.2, the decisions of bothPandEaffectE’s relative coordinate.Paims to control γPand θPby the threedegree-of-freedom control (13), whileEdirectly chooses(cosψ2cosψ1,cosψ2sinψ1,sinψ2)on the unit sphere as its motion is free.

III.EQUILIBRIUM STRATEGY IN 3D SPACE

In this section, we investigate the equilibrium strategy of bothPandEbased on the HJBI equation.According to the solution of the retrogressive path equations, we can divide the three-dimensional pursuit-evasion game into the following two phases.The Navigation phase aims to align the direction ofPtoE, while the Acceleration phase aims to approachEwith the fastest speed available.We also investigate the condition forPto captureEsuccessfully andE’s escape strategy whenPviolates this condition.

A. Pursuit-Evasion Process

As described in Sections II-B and II-C, the 3D pursuit-eva-

Fig.2.The relative coordinate system originating at P.

As the pursuit-evasion game terminates when the distanceris within εr,E’s relative coordinate directly determines whether the game reaches its terminal.Thus, we begin with the retrogressive path ofE’s kinematics (15) to catch a glimpse of the overall pursuit-evasion process.

According to (11), we obtain the RPE of (15)

Proposition 2 concludes the solution to the pursuit-evasion game according to (19)-(21).

Proposition 2:P’s state (v,θP,γP),E’s state (r,θE,γE), and the equilibrium strategysatisfy

Fig.3.The overall process of the pursuit-evasion game.P adjusts its pitch and yaw angles during phase N, and then concentrates on accelerating during phase A.If condition (26) always holds, P can successfully capture E, otherwise E can escape.

B. Conditions of Successful Capture

wherevmax(t) denotesP’s maximum allowable speed at timet.Furthermore,Ecan utilize the following strategy to escape whenPviolates the above condition (26):

Proposition 3 indicates thatP’s equilibrium strategy must maintain the speed undervmax(t) to guarantee a successful capture.As this criterion can be calculated immediately in practical applications, including air combats, missile guidance, and UAVs, the solution of the HJBI method supports a real-time decision in pursuit-evasion games.

C. Equilibrium Strategy During Phase N

As illustrated in Sections III-A and III-B,Paims to align withEduring phaseNbefore moving along the retrogressive path, with its speedv＜vmaxconstrained by (26).Thus, givingP’s pitch and yaw angles (θP,γP) andE’s relative coordinate(r,θE,γE), (30) providesP’s equilibrium strategy to align withE

D. Equilibrium Strategy During Phase A

After the alignment during phaseN,Paims to approachEduring phaseAwith ( θP,γP)=(θE,γE), andP’s speedv＜vmaxis constrained by (26).Meanwhile,Eaims to enlarge the distancerwith (ψ1,ψ2)=(θE,γE) to delay the capture, or utilize the strategy (27) to escape whenPviolates the condition (26).

Letv0denoteP’s speed at the beginning of phaseA, andTdenote the duration of phaseA.Under the constraint (26),P’s optimal control on its speed can be formulated as

where the constantk≜min{A2,A3}, and the terminal state isr(T)=εr.We have

Therefore, the constraintv≤kris equivalent to (34)

wherer0denotes the distance betweenPandEat the beginning of phaseA.

AsPaims to minimize the capture time,Pfirstly accelerates with φ1=A1duringt∈[0,t1).After then, sinceP’s maximum speed is constrained byvmaxin (26),Pmust decelerate with φ1=-A1duringt∈[t1,t2), and finally keepv=kεrto assure capture.Equation (35) shows the piecewise analytical form ofv

The final speedv(t2)=kεrindicates that

Furthermore, based on the terminal constraint=εr, we can derive the terminal timeT

whereT＜t2indicates thatEcan avoid capture.Otherwise,Pcan captureEif the constraint (38) holds

Thus,L(t) is a quadratic function with negative quadratic coefficient whent∈[0,t1), which indicates that

Similarly, sinceL(t) is a quadratic function with positive quadratic coefficient whent∈[t1,t2), we derive its minimum as follows:

According to (36) and (37), we have

Thus, the maximal accelerating timet1can be derived by analyzing all possible critical conditions

E. Overall Solution Framework

In the overall pursuit-evasion process, we derive the global equilibrium strategy according to the HJBI equation, which involves the navigation and acceleration phases.The global strategy can be summarized as (44)

The proposed equilibrium strategy guarantees the global optimality forPandE.First, (γP,θP) needs to align with(γE,θE)to ensure a successful capture.The equilibrium strategy reflectsP’s quickest way for alignment andE’s most efficient way for avoiding alignment.After then,P’s speed must satisfyv≤r×min{A2,A3} according to Proposition 3.The equilibrium strategy providesP’s optimal accelerating scheme under this constraint.WhenP’s speed exceeds the thresholdr×min{A2,A3}, the equilibrium strategy ensures thatEcan escape.Therefore,Pminimizes the capture time whileEmaximizes the capture time under this global equilibrium strategy.

Algorithm 2 The Equilibrium Strategy of P and E Input:A1, A2, A3, r,γE, θE, v0, γP(0), θP(0), v Output: P’s equilibrium strategy ( , , ), and E’s equilibrium strategy.θP ≠θE γP ≠γE φ1φ2φ3(ψ1,ψ2)1: if or then /* Navigation*/Δγ ←γE-γP 2:3: /* Refer to (30)*/Δθ ←θE-θP+2kπ 4: Calculate in (26)v ＜vmax vmax 5: if then φ1 ←A1 6:7: else φ1 ←-A1 8:9:φ3 ←A3 ∗sgn(Δγ)φ2 ←A2 ∗sgn(Δθ)10:11: Calculate by (31)12: else /* Acceleration*/t1, t2(ψ1,ψ2)13: Calculate via (43)14: Decide by (35)φ2, φ3 ←0 φ1 15:16: if then /* Escape scenario 1*/ψ1, ψ2 ←θE+ π v ＞r ∗A2 17:2,0 18: else if then /* Escape scenario 2*/ψ1, ψ2 ←θE, Lπ+ π v ＞r ∗A3 19:20: else /* Can not escape*/ψ1, ψ2 ←θE, γE 2-γE 21:22: return φ1, φ2, φ3, ψ1, ψ2

In practical combat scenarios, it is required thatPcapturesEwithin a limited timeT0.The following condition (46)determines whetherPcan captureEsuccessfully, given the initial states ofPandE:

where the duration timeTis calculated by (37).To determine the capture zone under the time limitT0, we need to calculatet1,t2andTby (43) for each distancer0, and then draw the region (r0,γE,θE) determined by the following inequalities:

IV.EXPERIMENTS

In this section, we conduct experiments to illustrate the proposed strategy under several situations.Experiment 1 shows the overall process of the pursuit-evasion game under the equilibrium strategy.Experiment 2 visualizes the capture zone ofP.Experiments 3-6 further compare the equilibrium strategy with its various deviations and illustrate the escape cases where the constraint (26) is not satisfied, in whichEadopts strategy (27) to escape successfully.

TABLE II EXPERIMENTAL SETTINGS IN DETAIL

A. Experimental Settings

Table II shows the detailed experimental settings involved in this section.Here (v0,θP(0),γP(0)) denotesP’s initial state,(x,y,z)denotesE’s initial relative position according toP, the polar coordinate (r(0),θE(0),γE(0)) is calculated from(x,y,z)=(rcosγEcosθE,rcosγEsinθE,rsinγE), and(v(T),θE(T),γE(T))denotes the terminal state.

Table II also shows the terminal states under different strategies, in whichTis the capture time,v(T) denotesP’s speed at timeT, (θE(T),γE(T)) denotesE’s relative coordinate at timeT.Besides, Table II provides the capture positions ofPandE.

In addition,P’s initial speed is 0.5 s-1, the step size of the simulation is Δt=0.02 s, and the terminal distance is εr=0.8.According to the flight maneuve√r controls designed by NASA[41], we set

B. Illustration of the Pursuit Strategy

Fig.4 illustrates the overall pursuit process when bothPandEadopt the equilibrium strategy.As Fig.4 shows,Pfocuses on changing its direction during phaseN.ThenPaccelerates to approachEafter it moves towardsE.Finally,PcapturesEwith the capture time 8.16 s.

Fig.4.Overall pursuit-evasion process under the settings of Experiment 1.The purple line denotes the current direction of v.The red and blue dots denote P and E, respectively.The red and blue stars denote the initial points of P and E.The dashed box denote the capture positions of P and E.

Fig.5 illustrates the change of pitch angle and yaw angle during both the Navigation and Acceleration phases.The dash lines denote γEand θE, while the solid lines denote γPand θP.Ptries to change its pitch angle and yaw angle during the timet≤0.32 s, then phaseNends and phaseAstarts with the initial speedv0=1.14 s-1and the initial distancer0=38.878,where the dash lines coincide with the solid lines.In addition,Fig.5 indicates that the curves of θPand θEapproximately keep straight during phaseA, which is consistent with Proposition 2.

Fig.5.The changes of the pitch angle, yaw angle, and distance.

Fig.6 illustratesP’s speed during the pursuit process, where the purple line denotes the maximum allowable speedvmax=rmin{A2,A3}, and the red line denotesP’s speed.According to the critical conditions given in (43), we have

Fig.6.P’s speed during the pursuit process.P accelerates with t 1=4.34 s,and then decelerates until successful capture.

which indicates thatt1≤4.34 s.

Thus,Pfirst keeps the minimum speedv0during phaseN,and then accelerates witht1=4.34 s.Finally,Pdecelerates to ensure thatP’s speed is always below the threshold.

Fig.7 shows the capture zone for various time limitsT0=9 s,10 s,11 s and 1 2 s.OnceP’s initial state (v,θP,γp) is given, (46) can be utilized to determine whetherPcan captureEwith initial position (r0,θE,γE) on time.

Fig.7.The capture zone for T0=9 s, 10 s, 11 s, and 12 s.The surfaces denote the boundaries of the corresponding capture zone and escape zone.

Fig.8 shows the change of average capture time according to the distancer(0) betweenPandE.The experiments are repeated 100 times for eachr(0)∈N∩[5,100), in whichP’s initial direction andE’s initial position are randomly and uniformly sampled.Fig.8 indicates that the success capture rate under the equilibrium strategy is 1 00%, and the average capture time grows with the increase ofr(0).

Fig.8.The change of average capture time.

C. Comparison With Various Deviations

According to the definition of Nash equilibrium [43], any unilateral deviation from the equilibrium strategy should be punished.Therefore, the capture should be slower whenPviolates the equilibrium strategy and faster whenEdeviates.We conducted experiments in Table III to verify whether this requirement is satisfied, and the detailed settings are listed in Table II.

Table III shows the differences whenPorEviolates the equilibrium.Compared with the equilibrium strategy adopted in Experiment 3,Paccelerates by 0.2 s more thant1in Experiment 4, corresponding to replacingt1byt1+0.2 s in (35).SinceP’s speed exceeds the threshold given in (26), this deviation leads to an escape scenario.

Experiment 5 assumes thatPdoes not accelerate during phaseN, which delays the capture time.Here,P’s strategy during phaseNcorresponds to replacing φ1=A1by φ1=0 s-2in (30).

Experiments 6 and 7 adopt a random strategy forEduring phaseNand phaseA, respectively.Here,E’s random strategy is (cosψ2cosψ1,cosψ2sinψ1,sinψ2) , in whichψ1is uniformly[samp]led from [0,2π), andψ2is uniformly sampled from -π2,π2.These two experiments are repeated 10 times with different random seeds, and the average result shows thatPwith the equilibrium strategy capturesEfaster.

D. Escape Scenario

Fig.9 illustratesE’s escape strategy whenP’s speed is above the thresholdvmax(t).The experiment settings are listed on Lines 3 and 4 of Table II, where Fig.9(a) corresponds to the equilibrium strategy, and Fig.9(b) corresponds to the escape scenario whereP’s acceleration time increases by 0.2 s.

Fig.9(b) indicates thatPcan not align withEwhenP’s speed is above the threshold, as highlighted by the blue box.Figs.10 and 11 clearly show the escape process: WhenP’s speed exceeds the threshold (as shown in Fig.11),Eimmediately turns to the strategy (27) (as shown in Fig.10), which preventsPfrom aligning withE, leading to a successful escape.

TABLE III COMPARISON RESULTS WITH DEVIATIONSK

Fig.9.Experiments on the acceleration phase.

V.FURTHER DISCUSSION

Our work aims at achieving real-time optimality for the realistic situation in the three-dimensional pursuit-evasion game.As the proposed equilibrium strategy can be immediately calculated, it supports real-time decisions for practical scenarios.

In our problem formulation, we follow the abstraction in typical pursuit-evasion game scenarios, where the pursuer follows a three-degree-of-freedom control, and the evader moves freely in the three-dimensional space with constant speed.Since our proposed solution to derive the equilibrium strategy for the three-dimensional pursuit-evasion game is based on the HJBI method, it can be naturally extended to scenarios where the evader has different kinematic equations.According to(23), the decreasing speed of distancer° is determined by〈eP,eψ〉, whereeψdenotes the evader’s movement that is not restricted to the free movement.Therefore, our proposed solution based on the HJBI method is still suitable whenEfollows other kinematics.Furthermore, the evader’s equilibrium strategy should maximize 〈eP,eψ〉 according to (23).

Fig.10.The pitch angle and yaw angle change when P’s speed exceeds the threshold.The blue box corresponds to the optimal strategy shown in Fig.9(b).

Meanwhile, our work still has the space for future extensions.One possible direction is that the three-degree-of-freedom model can be further refined to better adapt to the kinematics in realistic scenarios, such as the four-degree-of-freedom robotic fish [46], the six-degree-of-freedom unmanned combat aerial vehicle (UCAVs) [47], and the four-degree-offreedom pick-and-place robots [48].Similarly to the proposed three-degree-of-freedom kinematics, the trajectories of these agents are commonly determined by their velocities and directions controlled by the accelerations and turning angles.Therefore, by replacing the system kinematics in (13), our method has the potential to be applied to more complex and realistic scenarios.

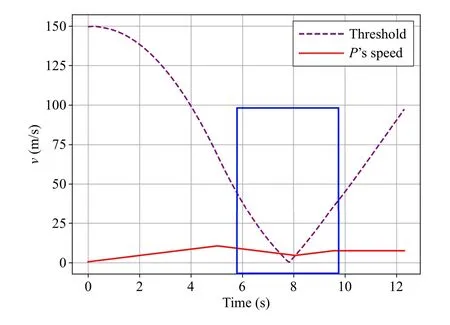
Fig.11.P’s speed during the escape scenario.

Another possible extension is that our problem formulation focuses on the one-pursuer, one-evader problem, which can be naturally extended to multiple pursuers and evaders.Although we can not directly derive the value functionV(x) for multipursuer scenarios with the HJBI equation due to the curse of dimensionality [23], our investigation in this paper reveals that the HJBI equation implies the phase separation of the overall pursuit-evasion process, which can be further utilized to derive the equilibrium strategy for pursuit-evasion games with more players.

In addition, real-world applications such as air combat, missile defense, and aerial dogfight have different sources of disturbances in players’ position, speed, and acceleration.Thus, a further extension is to tackle pursuit-evasion games with incomplete information to derive the equilibrium strategy in uncertain circumstances.

VI.CONCLUSION

This paper derives the equilibrium strategy of the realistic pursuit-evasion game in three-dimensional space with complete theoretical analyses.Based on the HJBI equation and the corresponding retrogressive path equation, we deduce that the equilibrium strategy consists of the Navigation and the Acceleration phases.In the Navigation phase, the pursuer should adjust its pitch and yaw angles to align with the evader while the evader attempts to delay the alignment.In the Acceleration phase, the pursuer accelerates to approach the evader.Furthermore, we provide a constraint for the pursuer’s speed to ensure a successful capture while giving an escape strategy when the pursuer’s velocity exceeds this limit.As the threedegree-of-freedom control is commonly used in practical situations, and the solution of the HJBI equation supports realtime decisions according to the derived threshold, the proposed equilibrium strategy has the potential to be employed in a wide range of applications in realistic scenarios.