混合随机波动模型下带随机工资的DC型养老金最优投资策略

邵艳宇，夏登峰，费为银，明 健

(安徽工程大学 数理与金融学院,安徽 芜湖)

随着科技发展,医疗水平不断提升,我国人口老龄化的增速加快,养老金支付压力剧增,制定养老金最优投资策略对实现养老金的保值增值以及提升退休人员生活质量起着至关重要的作用。养老金计划主要有两种：1)确定收益型(defined benefit,DB)养老金计划,参与者的收益是确定的,市场风险由基金管理者承担;2)确定缴费型DC养老金计划,参与者的缴费率是固定的,其收益主要取决于退休前的累积缴费值以及长期收益水平,市场风险由基金参与者承担,有利于缓解政府财政压力。因此,DC型养老金计划更符合我国社会发展体系的需要。

Merton[1-2]将随机控制方法应用于研究投资组合选择问题后,随机控制方法则被广泛应用于探究DC型养老金最优投资组合问题。大部分关于投资组合的文献[3-5]都假定风险资产价格服从几何布朗运动,价格波动率假设为常数。然而在实际金融市场环境中,风险资产的价格波动率是随机变动的。近年来,有学者开始提出Heston随机波动模型下的最优投资问题：Li等[6]研究Heston模型下保险公司的最优时间一致性投资和再保险策略;张初兵等[7]研究Heston模型下以最大化期望幂效用为目标的DC型养老金的最优投资问题;孙景云等[8]研究Heston模型下基于均值-方差准则的最优投资组合问题;Ma等[9]研究Heston模型下具有股票误定价的DC型养老金最优投资问题,应用随机控制理论建立了相应的HJB(Hamilton-Jacob-Bellman) 方程,并给出了在CRRA(constant relative risk aversion) 效用函数下的最优投资策略。

实际经济环境的变动往往会导致市场利率的随机波动。文献[10-13]对利率风险下DC型养老金的最优投资问题进行研究。Vasicek[10]利用随机利率模型O-U(Ornstein-Uhlenbeck) 描述利率动态变化过程。Cox等[11]提出CIR(Cox-Ingersoll-Ross) 模型模拟名义利率的动态变化。张初兵等[12]研究仿射利率模型下的DC型养老金最优投资策略。Mwanakatwe等[13]研究利率遵循Hull-White模型时的DC型养老金投资策略。

此外,也有学者同时研究随机利率和随机波动率下DC型养老金的最优投资问题。Guan等[14]探究具有随机仿射利率和Heston随机波动率的DC型养老金最优投资问题。Wang等[15]考虑DC型养老金计划的稳健性最优投资问题,其中随机利率和随机波动率分别由仿射利率模型和Heston随机波动率模型驱动。常浩等[16]研究在随机利率和随机波动率环境下的DC型养老金最优投资问题。Kim等[17]利用具有Hull-White利率模型和随机波动率模型的混合模型来评估期权价格对利率变化的敏感性,并表明了具有随机利率的随机波动率模型优于具有恒定利率的模型。Mwanakatwe等[18]研究混合随机波动(Heston-Hull-White) 模型下DC型养老金的最优投资和收益支付策略,并成功地给出了CRRA效用函数下的精确解。目前大多数文献采用CRRA效用函数来刻画投资者的风险偏好,然而,与CRRA效用函数相比,CARA(constant absolute risk aversion) 效用函数对风险的厌恶程度不依赖于当前财富水平,因此,本文采用CARA效用函数来刻画基金管理者的风险偏好。

由于养老金的投资期限较长,基金管理者不仅要考虑利率风险和波动风险,还要考虑随机工资。费为银等[19]研究了在CIR随机利率模型下带有随机工资的最优消费投资问题。Li等[20]在均值-方差准则下探究具有通胀风险和随机工资的DC型养老金最优投资策略。李方超等[21]在均值-方差准则下分析具有随机工资和保费退还条款的DC型养老金的时间一致性投资策略。Wang等[22]研究具有随机工资和通胀风险的DC型养老金最优投资策略。Yan等[23]分析具有随机工资和保费返还条款的DC型养老金稳健性最优投资策略。

为建立更符合实际金融市场的模型,本文根据文献[18-19]研究,在混合随机波动(Heston-Hull-White)模型中引入了随机工资,运用动态规划原理,得到在CARA效用函数下的最优投资策略,拓展了现有研究结果。本研究主要特点：1)假定金融市场中的股票价格服从混合随机波动模型,这更符合实际金融市场;2)在模型中引入了随机工资;3)采用CARA效用函数来刻画基金管理者的风险偏好。

1 模型建立

设(Ω,,{t}t≥0)为一个完备概率空间,且{t}t≥0满足通常条件,即{t}t≥0是右连续且-完备的,t表示截止到t时刻之前所有可用的信息。假设本文中的所有随机过程都定义在此概率空间上。此外,假设金融市场是无摩擦的,没有交易成本和税收且无卖空限制,且金融市场包括一种无风险资产和一种股票且可连续交易。

假设1无风险资产t时刻的价格S0(t)服从常微分方程式(1)。

(1)

式中：r(t)>0为无风险利率;s0为无风险资产的初始价格。

假设2金融市场中的股票在t时刻的价格S(t)满足混合随机波动(Heston-Hull-White)模型,其价格动态过程如式(2)所示。

(2)

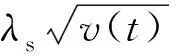
本文假定Wv与Wr相互独立,且Cov(Ws,Wv)=ρ1t,Cov(Ws,Wr)=ρ2t,其中ρ1∈[-1,1],ρ2∈[-1,1]。此外,为保证对∀t∈[0,T],v(t)>0恒成立,需要满足2κψ>σv2。

由于养老金的投资期限较长,因此考虑随机工资更加符合实际情况。本文假定t时刻的工资水平L(t)满足随机微分方程式(3)。

(3)

式中：μ>0为工资的期望增长率;σ为工资的波动率。

本文研究退休前的DC型养老金最优投资问题,假定参与者在退休日之前,按照工资的固定比例c向养老金个人账户持续缴费,养老金被允许投资在一种无风险资产和一种股票,并假设t时刻投资在股票上的资金比例是π(t),则t时刻投资在无风险资产上的资金比例是1-π(t)。定义X(t)为养老金在t时刻的财富,则DC型养老金的财富过程如式(4)所示。

(4)

定义1可容许策略。如果一个投资策略π(t)满足：1)∀t∈[0,T],π(t)是t可测的;随机微分方程;4)有唯一解;则称π(t)为可容许策略,记Π为所有可容许策略组成的集合。

在养老金积累阶段,基金管理者的目标是寻求一个最优投资策略π*(t),使得其终端财富的期望效用最大化,最优控制问题如式(5)所示。

(5)

本文选用CARA效用函数来刻画基金管理者的风险偏好,CARA效用函数可表示为

式中：q>0为风险厌恶系数。

2 最优投资策略

利用动态规划方法和变量分离法求解在CARA效用函数下的最优投资策略。定义值函数如下：

其中边界条件为V(T,x,r,v,l)=U(x)。

根据动态规划方法,假设V(t,x,r,v,l)∈C1,2,2,2,2([0,T]×R×R+×R+×R+),则V(t,x,r,v,l)满足HJB方程如式(6)所示。

(6)

式中：Vt、Vx、Vr、Vv、Vl、Vxx、Vrr、Vvv、Vll、Vxr、Vxv、Vxl、Vrl、Vvl分别表示V(t,x,r,v,l)关于变量t、x、r、v、l的一阶和二阶偏导数。

根据一阶最优条件可得最优投资策略如式(7)所示。

(7)

将式(7)代入式(6)可得如下偏微分方程：

(8)

假设方程(8)的解具有如下结构：

计算V(t,x,r,v,l)的各阶偏导数如式(9)所示。

(9)

将式(9)中各偏导数代入式(8)中可得

(10)

假设b(t,v)的形式为b(t,v)=A(t)+B(t)v,A(T)=B(T)=0

计算其偏导数可得

bt=At+Btv,bv=B,bvv=0

(11)

将式(11)中各偏导数代入式(10)中可得

化简得

通过分离变量,得到微分方程式(12)。

at+ar=0

(12)

(13)

At+(σrσvρ1ρ2qB-λr)A+κψB=0

(14)

(15)

(16)

解式(12)可得

a(t)=er(T-t)

(17)

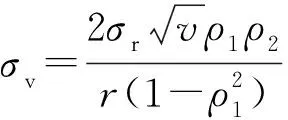
的根的判别式。若Δ>0,

若Δ=0,

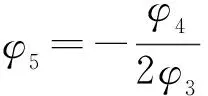
若Δ<0,

因此,式(13)的解为

(18)

解式(14)可得式(19)。

(19)

解式(15)可得式(20)。

(20)

解式(16)可得式(21)。

(21)

综上所述,可以得到以下定理：

定理1在CARA效用函数下,养老金终端财富的期望效用最大化的最优投资策略可表示为

值函数可表示为

其中,a(t)、B(t)、A(t)、m(t)、n(t)分别由式(17)、(18)、(19)、(20)、(21)给出。

3 数值分析

利用数值算例分析风险规避系数、利率参数和波动率等参数对基金管理者的最优投资策略的影响。本文采用文献[15,23]中的部分参数设置,基本参数设置如表1所示(另有说明的参数除外)。

表1 基本参数Table 1 The basic parameters

3.1 风险规避系数q对最优投资策略的影响

风险规避系数q对基金管理者的最优投资策略的影响如图1所示。由图1可知,股票的投资比例随风险规避系数的增加而降低。这是由于随着风险厌恶系数的增加,基金管理者对风险的厌恶程度增加。为了规避风险,基金管理者更倾向于减少对股票的投资,而增加对无风险资产的投资,这符合实际的市场情况,进一步说明模型的有效性。

图1 参数q对最优投资策略的影响Fig.1 Effects of parameter q on the optimal investment strategy

3.2 利率参数对最优投资策略的影响

利率参数对基金管理者的最优投资策略的影响如图2所示。由图2可知,随着利率的均值回复速度λr变大,利率对均值的回复时间变短,利率偏离均值水平的程度变小。因此,无风险资产的波动幅度减小,基金管理者更倾向于增加无风险资产的投资比例,而减少股票的投资比例。利率的波动率σr增加,表示利率风险增加,基金管理者更倾向于减少对无风险资产的投资比例,增加对股票的投资比例。

图2 参数λr和σr对最优投资策略的影响Fig.2 Effects of parametersλr and σr on the optimal investment strategy

3.3 波动率参数对最优投资策略的影响

波动率参数对基金管理者的最优投资策略的影响如图3所示。由图3可知,随着股票波动率的均值回复速度κ的增加,波动率对均值的回复时间变短,股票的价格变化幅度减小,股票的回报变得更加可预测,因此基金经理倾向于增加股票的投资比例。股票的方差波动率σv越大通常意味着股票的波动风险越高,因此基金经理倾向于降低股票的投资比例以避免风险。

4 结 语

在DC型养老金最优投资问题中,基金管理者需同时考虑利率风险、波动风险和随机工资具有现实意义和理论价值。利用动态规划方法,通过求解HJB方程,得到在CARA效用函数下的最优投资策略。通过数值算例分析了风险规避系数、利率参数和波动率参数对最优投资策略的影响。研究结果表明：随着风险规避系数的增大,投资于股票的比例显著下降;利率均值回复速度和股票的方差波动率的增加均会导致投资于股票的比例下降,而利率波动率和股票均值回复速度的增加均会导致投资于股票的比例上升。本文不仅扩展了原有的模型,而且使得扩展后的模型更贴近实际市场。研究结果对基金管理者的投资决策具有一定的现实指导意义,为后续的研究提供一定的理论基础。