考虑时滞的自平衡车控制系统稳定性分析

易奎辰，曾红兵，梁津铭，李新宇

（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

1 研究背景

两轮平衡车是一种类直线倒立摆结构模型，主要由两个同轴分布的车轮和两个独立的电机组成，能够自动维持姿态平衡[1]。因其具有结构简单、控制灵活，节能环保，能够适应多种复杂场合的优点，目前已在民用、安保、工业和军事等领域被广泛投入使用，并逐渐成为移动机器人研究的重要领域[2-3]。

两轮自平衡车的平衡控制系统是其核心部分，主要包括传感器、控制器和执行器。传感器主要用于实时检测车辆的倾斜角度和角速度，常用的传感器有加速度计和陀螺仪[4]。控制器根据传感器的信号计算出合适的控制指令，以保持车辆稳定。执行器则根据控制器的指令驱动轮子旋转，从而实现车辆自平衡。目前常见的控制策略有比例-积分-微分（PID）控制[5]、模糊控制[6-7]、最优控制LQR（linear quadratic regulator）[8]、神经网络控制[9]等。国内外学者们虽然对平衡车进行了大量的研究，但是当前自平衡车的控制策略往往没有考虑时滞给平衡车控制系统带来的影响，例如传感器采集数据的延迟、控制器计算延迟，以及执行器响应延迟等，忽略时滞的影响不仅会使平衡车控制系统稳定性下降，也会使其控制性能降低[10-12]。因此，在设计自平衡车的控制策略时，应充分考虑传输时滞问题。

当前关于时滞相关稳定性问题的研究中，主要采用的方法是时域法。Lyapunov-Krasovskii（L-K）泛函方法是时域法中的主要分析方法，其基本思路如下：首先，构造一个正定有界L-K泛函，然后对其求导，通过确定导数的负定条件来确定系统的稳定性，这类稳定性条件一般表述为线性矩阵不等式（LMI）的形式。此类方法获得的稳定判据具有一定的保守性。为了得到更低保守性的稳定判据，可以从泛函的构造与对其导数的处理两个方面来实现[13]。其中泛函的构造一般分为简单型、增广型、完全型、离散型，以及时滞分割型等[14]。其中，简单型泛函是在经典李雅普诺夫二次型函数上增加含时滞二次项得到的，虽然其结构简单，但所得结果往往保守性较大；完全型泛函虽可获得系统渐近稳定的充要条件，但因其维数无限大，难以求解验证；离散型泛函对于时变时滞系统存在难以求解的问题；时滞分割型泛函对于分段的数目增加，计算将变得非常复杂。故本研究拟采用增广型泛函，在简单型泛函的基础上进行增广，以包含更多的时滞信息，从而得到计算较简单、保守性较小的稳定判据[15]。处理泛函导数中存在的二次型积分项方法一般分为模型变换法、自由权矩阵法和积分不等式法[11]。因时滞系统中模型的变换与积分不等式的界定都不可避免地会带来保守性，故自由权矩阵法是当前时滞系统研究中常用的方法。针对现阶段自平衡车控制策略存在的问题，本研究考虑两轮自平衡车控制系统的时滞相关稳定性。首先，建立了多PID控制器的平衡车系统整体状态空间模型；然后应用L-K 泛函方法和自由权矩阵积分不等式技术，建立了一种基于文献[16]的新时滞相关稳定判据；接下来通过LMI 工具箱求解，得出不同速度环PID 参数下的最大时滞上界；最后，通过仿真结果验证所得结果的准确性。

2 自平衡车系统模型

2.1 坐标系建立

对自平衡车进行瞬时力学分析前，需要建立空间直角坐标系。本文建立的自平衡车坐标系如图1 所示。其以自平衡车左右两轮轴中心点为参考坐标系的原点O（X-Y-Z），以左右两轮轴线并由左轮指向右轮方向为X轴，以过原点并和重力相反的方向为Z轴，以垂直X轴和Z轴并指向前进方向为Y轴。

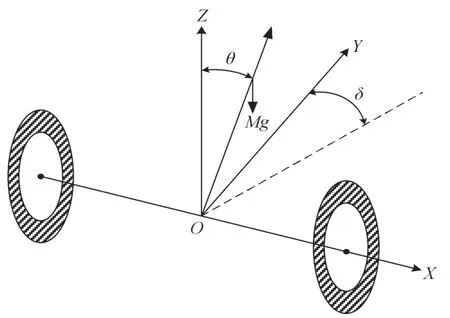
图1 自平衡车坐标系Fig. 1 Self-balancing vehicle coordinate system

2.2 牛顿力学模型建立

自平衡车轮轴的中心位移x与其左右轮的位移关系如下：

自平衡车的偏航角δ与其左右轮的位移满足下式：

式（1）（2）中：D为左右轮间距离；

x1、xr分别为左右轮的位移，且

其中θl、θr分别为左右轮转过的角度；R为左右轮的半径。

图2 为自平衡车左轮受力分析图。

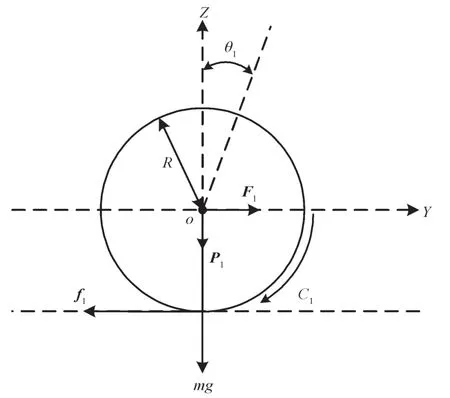
图2 自平衡车左轮受力分析图Fig. 2 Analysis diagram of left-wheel force of the self-balancing vehicle

对自平衡车左轮进行受力分析，建立如下力学平衡方程：

同理可得如下右轮力学平衡方程：

式（5）～（8）中：m为左右轮的质量；

fl、fr分别为左右轮受到的地面摩擦力；

Fl、Fr分别为左右轮与平衡车体在水平方向的作用力；

Cl、Cr分别为左右轮转矩；

Jω为左右车轮转动惯量，且。

平衡车体的力学方程如下：

式（9）～（12）中：M为平衡车体的质量；

L为质心到轮轴的距离；

θ为平衡车摆杆倾斜角；

Jp为平衡车体对x轴的转动惯量，且；

xp为质心的水平位移，且

yp为质心的垂直位移，且

P1、Pr分别为左右轮与平衡车在垂直方向作用力；

Jδ为平衡车对y轴的转动惯量，且。

当平衡车在平衡点附近时，θ≈0、sinθ≈0、cosθ≈1，联立方程（1）～（13），化简可得[17-18]：

2.3 直流电机线性建模

两轮自平衡车控制电机采用的是两个直流电机，直流电机的线性化模型如图3 所示。

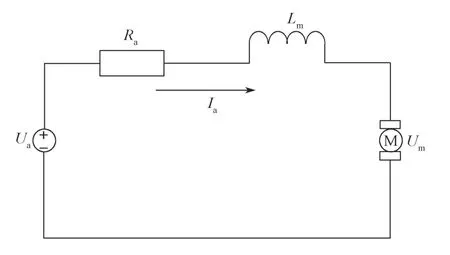
图3 直流电机工作原理示意图Fig. 3 DC motor working principle diagram

电机输出电压Ua与电机转矩Cm之间的关系式如下[19]：

式中：Km为电机转矩系数；

Ua=RaIa+Um，其中Ia为电枢电流，Um为电机转子反电动势；Ra为电机转子等效电阻；Ke为电机反电动势系数；θm为电机转子角度。

2.4 系统状态方程

当θ=±5°时，输入变量，状态变量，则含时滞的双轮平衡车状态方程可表示如下：

式中：τ(t)为传输时滞；

X(t)为t时刻状态向量；

U(t)为输入，Ul、Ur分别为左右电机控制电压；

A1、A2、B1为系统矩阵；

C为输出矩阵。

将式（18）代入式（15）～（17）写成式（19）形式，可得：

含传输时滞的自平衡车系统控制模型如图4 所示。

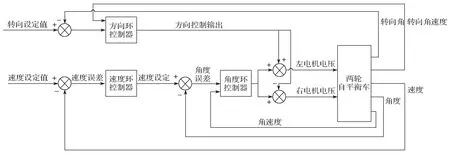
图4 自平衡车控制系统框图Fig. 4 Block diagram of the self-balancing vehicle control system

自平衡车系统的速度环采用如下PI 控制器：

式中：uv为速度环输出；

vd、vb分别为设定的目标速度与速度反馈。

角度采用如下PD 控制器：

式中：ua为角度环的输出；

θd、θb为目标角度与角度反馈；

在此控制模型中，角度控制环的输入为速度控制环的输出，即θd=uv。

方向控制器采用PD 控制：

式中：us为方向环的输出；

δd、δb分别为目标偏航角与偏航角反馈；

自平衡车控制系统中输出为左右轮电机电压：

通过以上分析，可构造如下输出控制反馈系统：

将系统（24）简化可得如下线性系统：

0 ＜τ(t) ＜τ；

φ(t)为初始状态。

3 稳定判据

为建立系统（25）的稳定性条件，需要用到如下引理。

引理1[16]设表示m维向量空间，x是一个连续可微函数：[α,β]→Rn，diag表示对角矩阵，I为单位向量矩阵。对于任意矩阵，，有以下不等式成立：

式中：

为简化矩阵和向量的表达，首先定义以下符号：

构造增广型L-K 泛函，并应用引理1 给出的积分不等式，推导出如下自平衡车控制系统稳定判据。

定理1对于给定的标量，μ1＜μ2＜1，τ＞0 如果存在矩阵使得式（27）（28）成立，则系统（25）是渐近稳定的。

式中：j=1, 2；为n×m维实矩阵；为n×n维对称正定矩阵。

式中，0 为合适维度0 矩阵。

证明选取如下L-K 泛函：

对V(t)求导，可得：

用引理1 来估计V(t)导数中的积分项，可得：

式中，

由定义的向量ξ(t)可得，对于任意矩阵S1、S2、S3、S4，下列等式成立[20]：

4 仿真结果与分析

对于系统（25），采用表1 各项参数进行系统建模与Simulink 仿真验证。

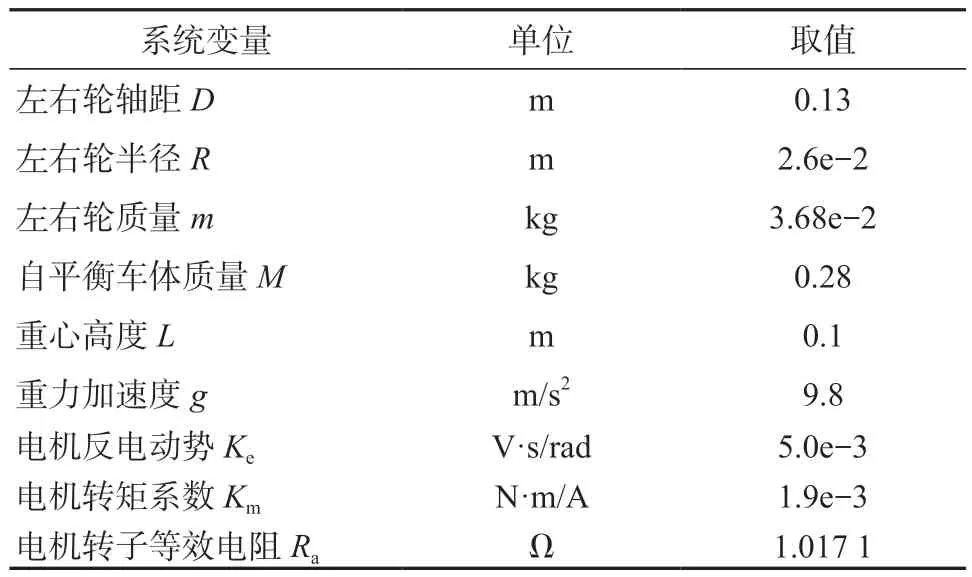
表1 自平衡车参数设置Table 1 Self-balancing vehicle parameters

当μ=0 与μ=0.5 时，固定角度增益KaP=80,KaD=8与偏航角增益KsP=10,KsD=3；变化速度增益（KvP由0.1～0.5，KvI由0.01～0.03）。由稳定判据计算得到的保证系统（25）稳定允许的最大时滞上界见表2。

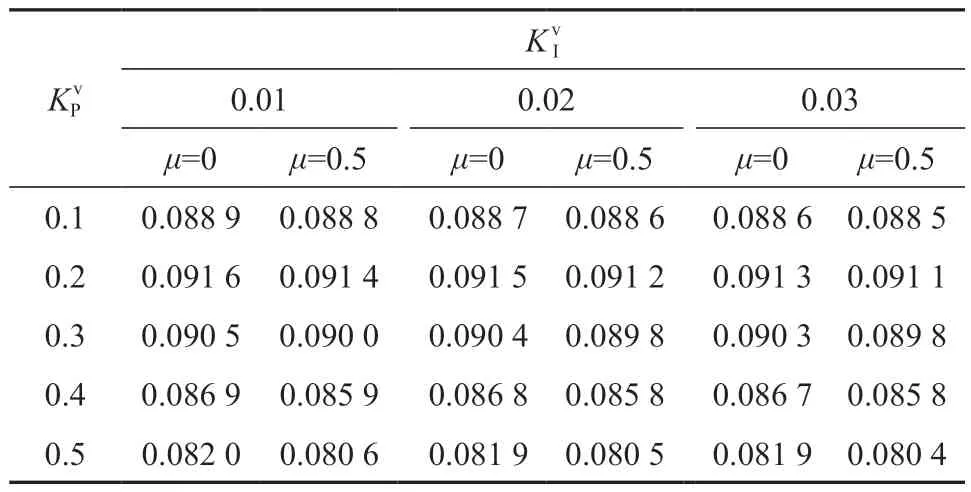
表2 （K vI，K Pv）分别取不同参数时的时滞最大上界（定常时滞μ=0 和μ=0.5）Table 2 Delay stability margin for different PI gains(with μ=0 constant time delay and μ=0.5 time-varying delay)

为了验证上述结果的准确性，选取速度环的控制参数KPv=0.3，KvI=0.03；角度环的控制参数KPa=80，KDa=8；方向环控制参数KPs=10，KDs=3；初始时刻角度为θ=10°，由Simulink 仿真，所得结果如图5 所示。

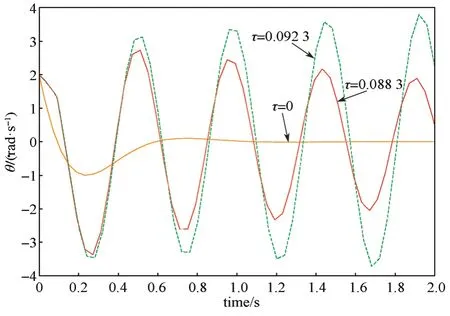
图5 不同时滞的系统角速度偏移Fig. 5 Angular velocity shifting of the system with different time delays

由图5 所示仿真结果可知：τ= 0 s 时，自平衡车系统大约经过1 s 后保持稳定；τ= 0.088 3 s 时，系统逐渐收敛；τ= 0.092 3 s 时，系统变为发散不稳定的情况。这说明保证自平衡车系统稳定的时滞最大上界在0.088 3～0.092 3 s 这一区间范围内，而表2 中通过LMI 求解出的时滞上界为0.090 3 s，正好在这一区间范围内，表明了文章中构造的稳定性判据的有效性和计算出的时滞稳定裕度的准确性。

5 结语

文中针对两轮平衡车系统的非线性、多变量、强耦合等特性，对其进行了建模与线性化解耦，构造出自平衡车系统的状态空间模型。其次，考虑了系统传输时滞的影响，运用基于自由权矩阵积分不等式的方法，建立了系统的时滞相关稳定性判据。最后运用Simulink 仿真，验证了该系统稳定性判据的有效性。因此文中提出的时滞稳定裕度可以作为附加指标，指导考虑时滞影响的控制器设计。同时，因本方法计算出的时滞最大上界能较为准确地评估时滞对机器人自平衡能力的影响，故本文计算时滞稳定裕度的方法可为控制器设计提供新思路。