焊接锚垫板锚固区拉压杆模型及配筋设计

王赞芝, 杨春旭, 钟洋, 李先一

(1.广西科技大学土木建筑工程学院, 柳州 545006; 2.中铁隧道局集团有限公司勘察设计研究院, 广州 511458)

随着公路桥梁建设规模的持续发展,后张法预应力结构被广泛应用于高强、轻质以及大跨度桥梁工程中[1-2]。在后张法预应力结构中,锚具作为主要的预应力材料,锚具中的锚垫板常使用铸造方式生产。由于铸造方式生产锚垫板耗能高、效率低,特别是对环境的污染严重,已不符合中国现行的低碳环保政策,因此有必要改进锚垫板的生产方式。2017年12月,广西壮族自治区科技厅下达了科技计划“高强环保型预应力用锚垫板的研制及示范应用”(桂科AB17292022),该项目以钢板为原料,通过冲压与焊接结合的方法生产锚垫板,开展系列的相关研究[3-4],对公路桥梁中使用焊接锚垫板时,其齿板的锚固区受力性能进行研究。

公路桥梁受力大,预应力筋布置多,往往在箱梁的顶、底板等处设置多个齿板,其承担着将预应力扩散至梁体的作用,由于集中力作用、锚具的制造工艺不同和结构几何尺寸的变化,会产生使结构开裂和失效的应力集中效应。根据圣维南原理,齿板锚固区域不再满足平截面假定,传统设计方法不能很好地对该区域进行有效配筋,在国际混凝土结构设计中将该类混凝土受力构件分为Beam(B区)和Discontinuity(D区)[5-8]。对于整体结构而言,出现应力流不连续,或应力扰动的区域,以及几何结构不连续的区域,这些显然不符合平截面假定的区域称为D区,与之相反的规则区域则称为B区。在处理D区抗裂配筋问题过去常采用经验方法和试算配筋方法,缺乏一种有依据的设计方法,以至于D区在设计精度上无法得到满足。D区的受力分析和配筋设计一直是预应力混凝土研究领域的难点和热点问题[9-10]。工程中因后张法配筋不合理导致的构件开裂甚至破坏的案例也有很多[11-12]。

在锚固区设计过程中,常通过改善锚具传力性能予以规避锚固集中力和几何尺寸的改变对整体结构所造成的应力扰动[13]。在使用焊接锚垫板时,这类新型锚垫板与常规铸造锚垫板相比,对锚固区周围应力扰动,尤其是端部锚点的影响更为明显,需重点关注。中外学者已针对预应力引起的应力扰动现象开展大量研究。蒋欣等[14]针对箱梁端部锚固区劈裂力计算不明确的情况,建立了基于“两刚片规则”的静定拉压杆模型,将计算结果与规范结果对比,证明了模型的可行性。Xia等[15]提出了一种考虑多荷载组合情况下的优化拉压杆模型,并将其用于D区设计。Zhou等[16]开发了一种新型拉压杆模型用于预测锚固区在弹性和非弹性受力过程中的力学行为,并通过试验验证了其准确性。Fazeli等[17]针对孤立的钢筋混凝土开孔承压构件,提出了预测开孔构件承载能力的拉压杆解析模型,并与各国规范进行了对比,验证了模型的合理性。由等效的拉压杆件和节点组成的拉压杆模型能较为真实地反映构件的受力情况,是解决复杂应力问题的有效方法,目前,美国国家公路与运输官员协会(American Association of State Highway and Transportation Officials,AASHTO)Load-and-resistanceFactorDesignBridgeDesignSpecifications[5](下文简称AASHTO规范)、BuildingCodeRequirementsforStructuralConcreteandCommentary(ACI 318-19)[6](下文简称ACI 318-19规范)和欧洲CEB-FIP99设计建议PracticalDesignofStructuralConcrete[7](下文简称CEB-FIP99)也均认为拉压杆模型是解决D区混凝土受力问题的重要工具,中国现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[8]也在附录中引入拉压杆模型。拉压杆模型构形方法主要有应力迹线法、荷载传递路径法和最小应变能法等。其中应力迹线法使用较为简单明了,且能真实反映结构力流传递方向[18],以此作为构形方法能使拉压杆件中心与真实传力方向很好的吻合,保证配置的钢筋能均匀分布在裂缝出现的区域,可获得合理的配筋方案。

鉴于此,在分析焊接锚垫板齿板锚固区的横向应力分布、应力迹线以及6种典型效应量化指标的基础上,通过有限元分析,拟合锚固区劈裂力合力重心计算式。提出一种新型的齿板锚固区拉压杆模型,并针对焊接锚垫板齿板锚固区进行配筋设计,可为焊接锚垫板齿板锚固区实际工程应用提供理论基础。

1 锚固区的拉压杆模型构形方法

1.1 齿板锚固区应力分布特征

在预应力混凝土桥梁中,由于施工张拉、锚具变形等原因,箱梁齿板锚固区受力较为复杂,如图1所示。通过有限元模型进行锚固区应力分析,结合《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[8]可知,齿板锚固区应力分布特征可以归结为以下6种典型应力集中效应:①张拉预应力作用下的锚下劈裂效应;②锚固区偏心引起的牛腿效应;③锚固区对锚后区域产生的锚后牵拉效应;④底板因局部弯曲产生的弯曲效应;⑤钢束弯曲段的径向力效应;⑥水平剪切效应,各效应产生的裂缝如图2所示。

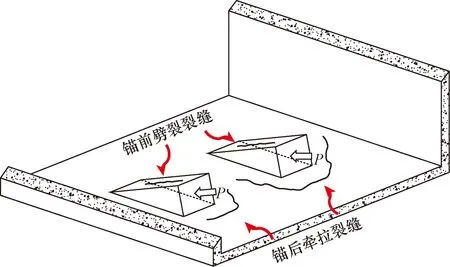
P为锚固力图1 箱梁齿板锚固区Fig.1 Anchorage area of blisters in box girder

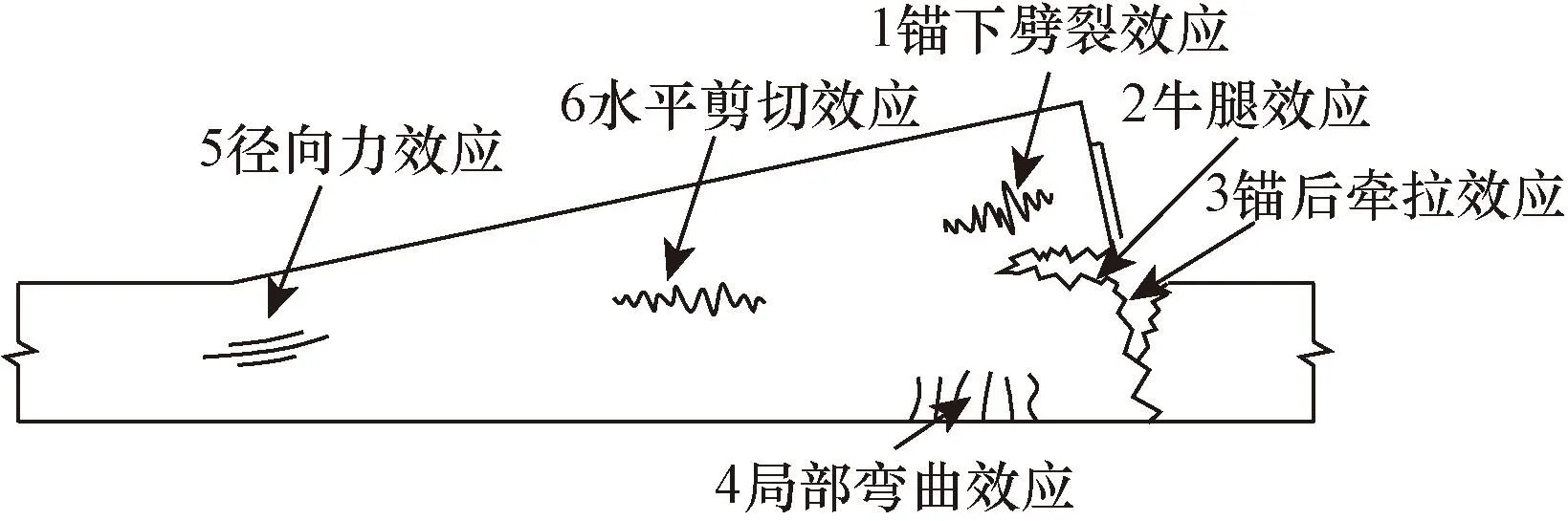
图2 齿板锚固区6种典型应力效应及对应的裂缝Fig.2 Six typical stress effects and their corresponding rents anchorage blisters

贺志启等[19]对弹性受力阶段的齿板锚固区应力分布进行探究,提出了锚后约束完全自由的拉压杆模型,但在实际工程中齿板锚后约束往往处于自由与完全固结之间。通过有限元分析可知,从图3可以看出,应力分布表现为以锚固点为原点的中心对称分布,锚前和锚后应力大小相等方向相反。在图3(a)中,锚前区域主要以压力扩散,导致混凝土横向受拉产生劈裂破坏,锚后区域主要以拉力扩散,引起混凝土的横向受压。图3(b)中,主应力迹线反映力的传递方向,锚固力在锚前区域以压应力扩散,在锚后区域以拉应力扩散,距离锚固点越远,锚前和锚后应力均匀分布于底板,且各分配了50%的荷载。

图4所示的立面主应力迹线与图2所示的典型应力效应形成对应关系。同时,锚前压应力迹线和锚后拉应力迹线逐渐收拢且均匀分布于底板,锚固区内由锚前和锚后扩散的力约为50%,这表明图3与图4应力迹线有着相似的结果。

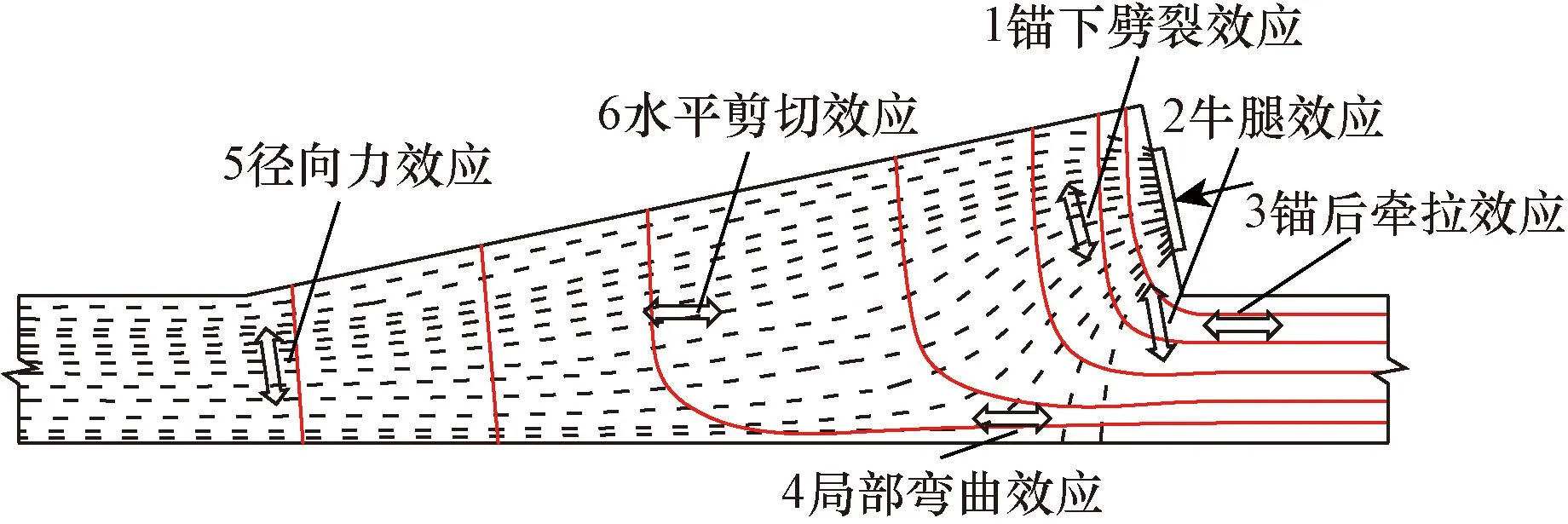
图4 齿板立面主应力迹线Fig.4 Principal stress traces blisters elevation

图5为隔离体分析6种局部效应力流的平衡关系。

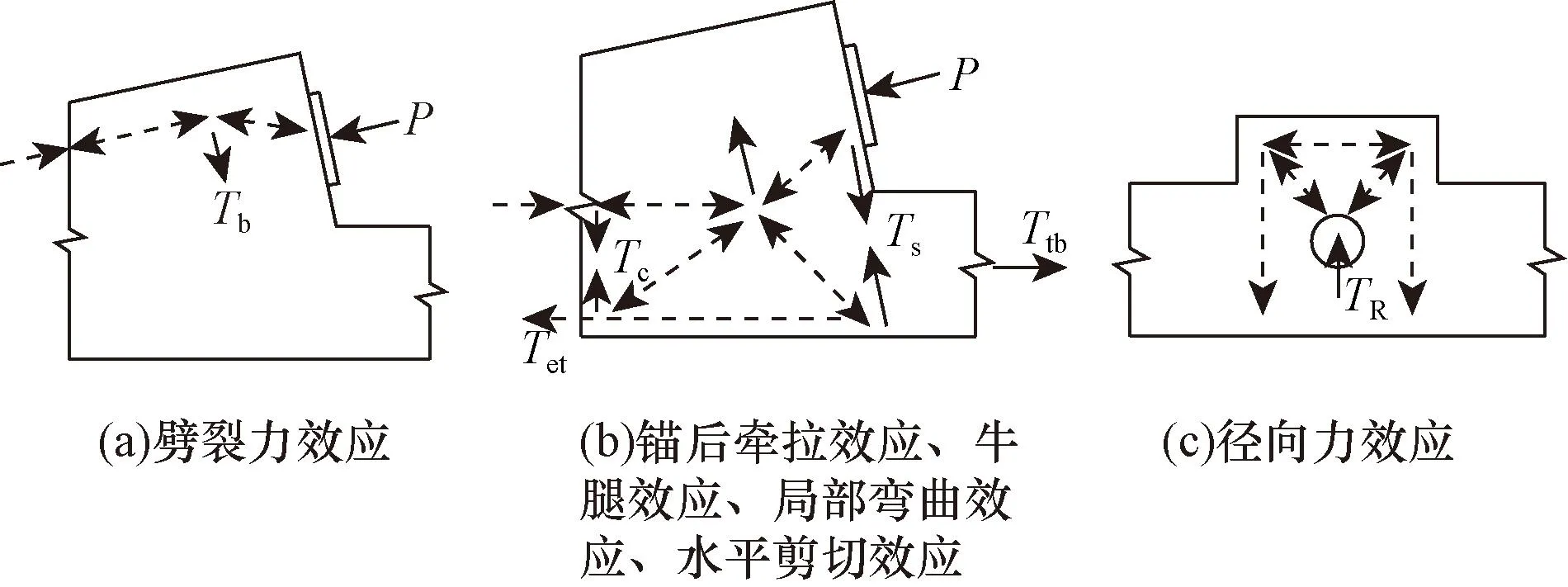
P为锚固力;Tb为锚下劈裂力;Ts为牛腿效应产生的拉力;Ttb为锚后牵拉力;Tc水平剪切产生的拉力;Tet为弯曲效应产生的拉力;TR为径向力图5 6种局部效应力流平衡关系Fig.5 Six local effect force-flow balance relations

1.2 拉压杆模型的基本构形

在前述应力分布、局部力流平衡关系以及平面立面应力迹线分析的基础上,为得到与原结构受力相同的拉压杆模型,还需要确定各杆件和节点的位置以及倾角等参数。根据模型的几何特征以及锚固区应力分布特点可确定应力迹线对应的拉压杆位置,可建立如图6所示的焊接锚垫板下锚固区拉压杆模型。

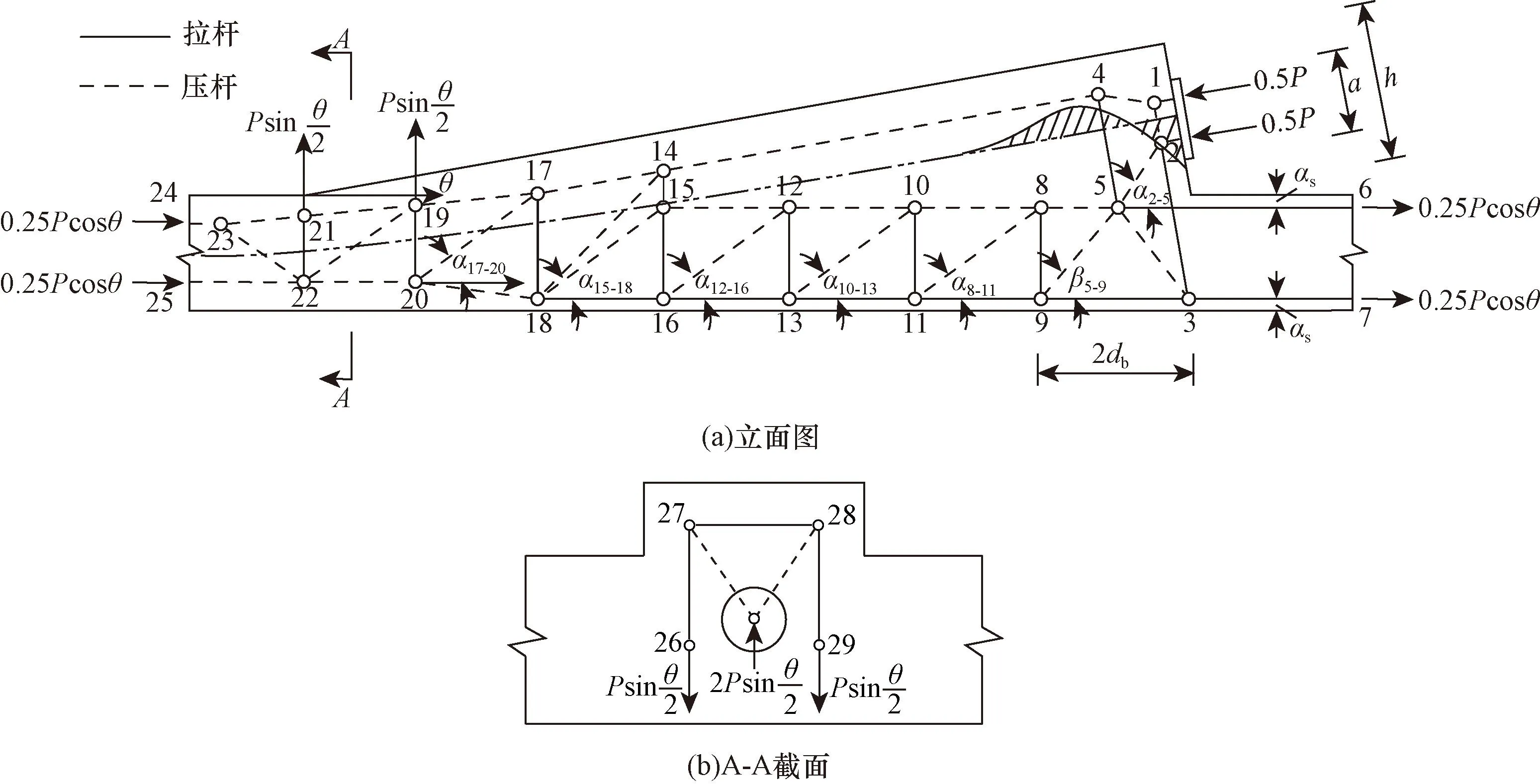
1～29为节点;θ为齿板倾角;α2-5、α8-11、α10-13、α12-16、α15-18、α17-20和β5-9为压杆与水平方向倾角;db为劈裂力重心至锚固端距离;a为锚垫板底板直径图6 齿板锚固区拉压杆模型Fig.6 Strut-and-tie model for the anchorage blisters

其中,张拉预应力在锚固区的扩散可采用压杆1-4和压杆2-5模拟;锚下劈裂效应产生的拉应力通过拉杆4-5模拟;根据立面应力迹线可知,力筋轴线与锚固区上部边缘的压应力场均匀,采用平行于上部边缘压杆4-14和压杆14-17模拟;锚前应力迹线逐渐向底板传递,采用5号至15号节点间水平压杆以及斜压杆5-9、8-11、10-13、12-16、14-18、15-18、17-20模拟锚固预应力向底板传递;桁架模型的受拉腹杆以及竖向拉杆14-15、17-18、19-20保证了结构内力的平衡;结构转向区域压杆19-22和压杆22-23对拉杆21-22提供了锚固作用。为保证焊接锚垫板拉压杆模型的合理性,将6种作用效应与拉压杆模型关系进行比对,如表1所示。通过本模型进行结构配筋设计,能使焊接锚垫板锚固区抗裂承载能力得到加强。

表1 6种典型应力效应与拉杆对应关系Table 1 Six typical stress effects vs. ties

拉压杆模型是由力流模型抽象而成的桁架模型,其中拉杆、压杆以及节点位置通过以下阐述得到。

(1)预应力在箱梁中根据锚固位置不同,可分为端部锚固和中间锚固,不同锚固方式有着不同的边界条件。其中中间锚固的受力同端部锚固受力相比较复杂,在受到外荷载时,荷载向锚前和锚后同时扩散,锚前产生压力,锚后产生拉力。为解决中间齿板锚固区的受力特点问题,需要计算出荷载在锚前和锚后传递的比例。根据美国AASHTO规范[5]规定,锚后钢筋至少需分配25%的荷载,但规范未给出定量化的计算模型。有学者通过有限元模拟和光弹实验得出[19-21],锚后分配荷载至少为锚固力的50%。与齿板锚固区平面和立面应力迹线所显示的50%锚后牵拉力基本一致。

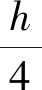
(3)影响5号节点位置的因素相对较多,该节点位置控制的局部区域较广,对锚固力有着传递和传向作用,而抵抗劈裂力以及锚后牵拉作用效应的钢筋也穿过该节点区域。压杆2-5通过节点将力传向锚前,为保证力的传递不发生水平剪切破坏还需确定压杆2-5的与水平方向的倾角α2-5,倾角需满足摩擦剪切理论[5]提出的最小倾角要求[最小倾角取值范围参考(4)],如不满足可对锚后牵拉力筋位置进行调整。

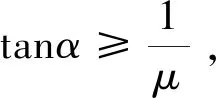
(5)根据上述拉压杆几何构形的分析,拉压杆模型最终还需确定拉杆4-5位置。为保证焊接锚垫板下劈裂力配筋有效,根据研究表明拉杆位置与劈裂力合力重心位置重合时,锚下裂缝控制能得到加强,因此,劈裂力合力重心位置对锚下劈裂效应配筋起着重要作用,可用来表示拉杆位置。参考欧洲CEB-FIP99[7]设计建议可知,劈裂力合力重心位置与焊接锚垫板尺寸a和齿板截面尺寸h相关,对于齿板锚固区而言劈裂力合力重心位置还与齿板倾角θ相关。根据焊接锚垫板直径的不同,现有的焊接锚垫板分为3孔、4孔、5孔等,在齿板倾角θ=10°不变的情况下,通过有限元数值分析得到不同尺寸的焊接锚垫板锚下劈裂力分布,如表2所示,其中劈裂力合力重心位置可通过沿齿板孔道轴线的劈裂力积分得到。将表2中的数据进行拟合,结果如图7所示。对不同孔径所对应的劈裂力合力重心位置进行分析,利用线性回归进行拟合,可得

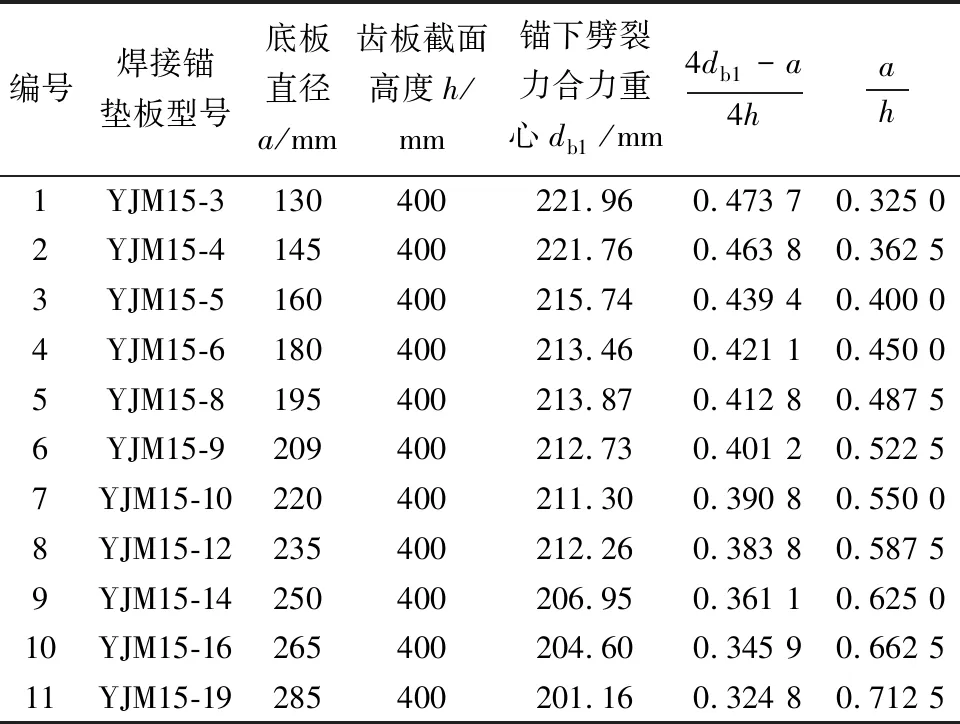
表2 不同锚垫板直径对应的劈裂力合力重心位置Table 2 The center of gravity location of bursting center of gravity for different bearing plate diameters

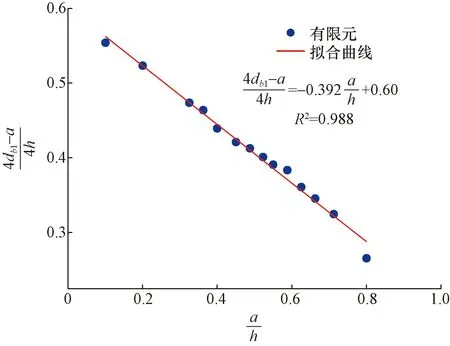
图与曲线(θ=10°)

db1=-0.142a+0.6h

(1)

式(1)中:db1为劈裂力合力重心至锚固端面距离。

锚下劈裂力合力重心位置还与齿板倾角θ相关,根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》应用指南[22]可知,力筋弯起角θ一般在15°范围以内,考虑齿板布置位置及混凝土用量的经济性,θ在10°～15°取值,取表2中编号1探究θ与db关系,如表3所示。将表3数据进行拟合,拟合结果如图8所示。得到考虑倾角θ影响的劈裂力合力重心公式为

图与曲线

(2)

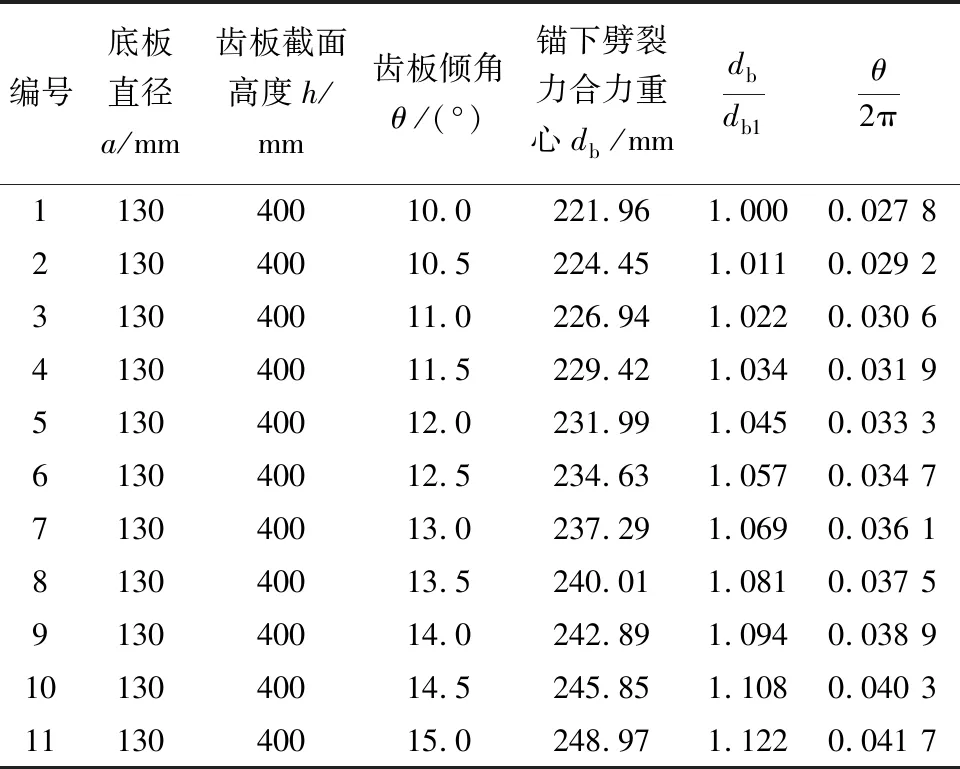
表3 不同齿板倾角对应的劈裂力合力重心位置Table 3 the center of gravity location of bursting force for different blisters inclination angles

将式(1)代入式(2)中,可得到焊接锚垫板锚下劈裂力合力重心计算公式为

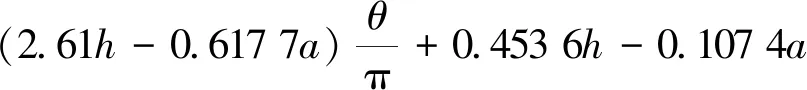
(3)

式(3)中:a为锚垫板底板直径。

根据式(3)和拉压杆模型几何关系可得焊接锚垫板锚下劈裂力计算公式为

(4)

为验证式[式(1)～式(4)]的正确性,将上述计算公式[式(1)～式(4)]结果与不同规范和有限元结果进行对比,如图9和图10所示。结果显示式(3)和式(4)所得到的齿板锚固区劈裂力合力重心位置和劈裂力大小与有限元结果符合的较好;而美国AASHTO规范[5]和欧洲CEB-FIP99[7]设计建议所得结果只考虑了端部锚固的情况,因此,在计算齿板锚固区劈裂力合力重心位置和劈裂力大小时结果误差相对较大,本文计算公式更加精确且更适用于焊接锚垫板齿板锚固区。

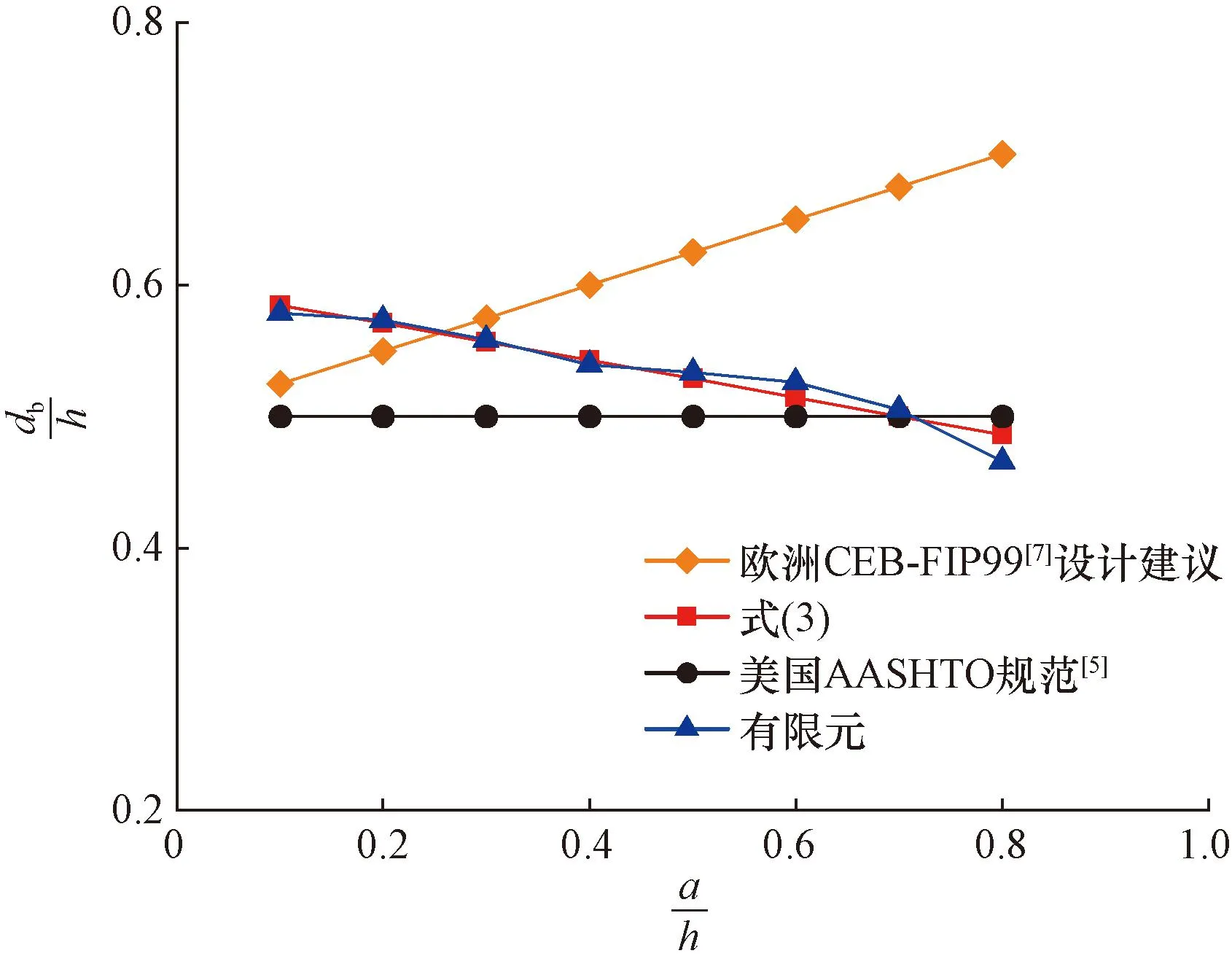
图9 劈裂力合力重心位置对比(θ=10°)Fig.9 Comparison of the center of gravity location of bursting force(θ=10°)

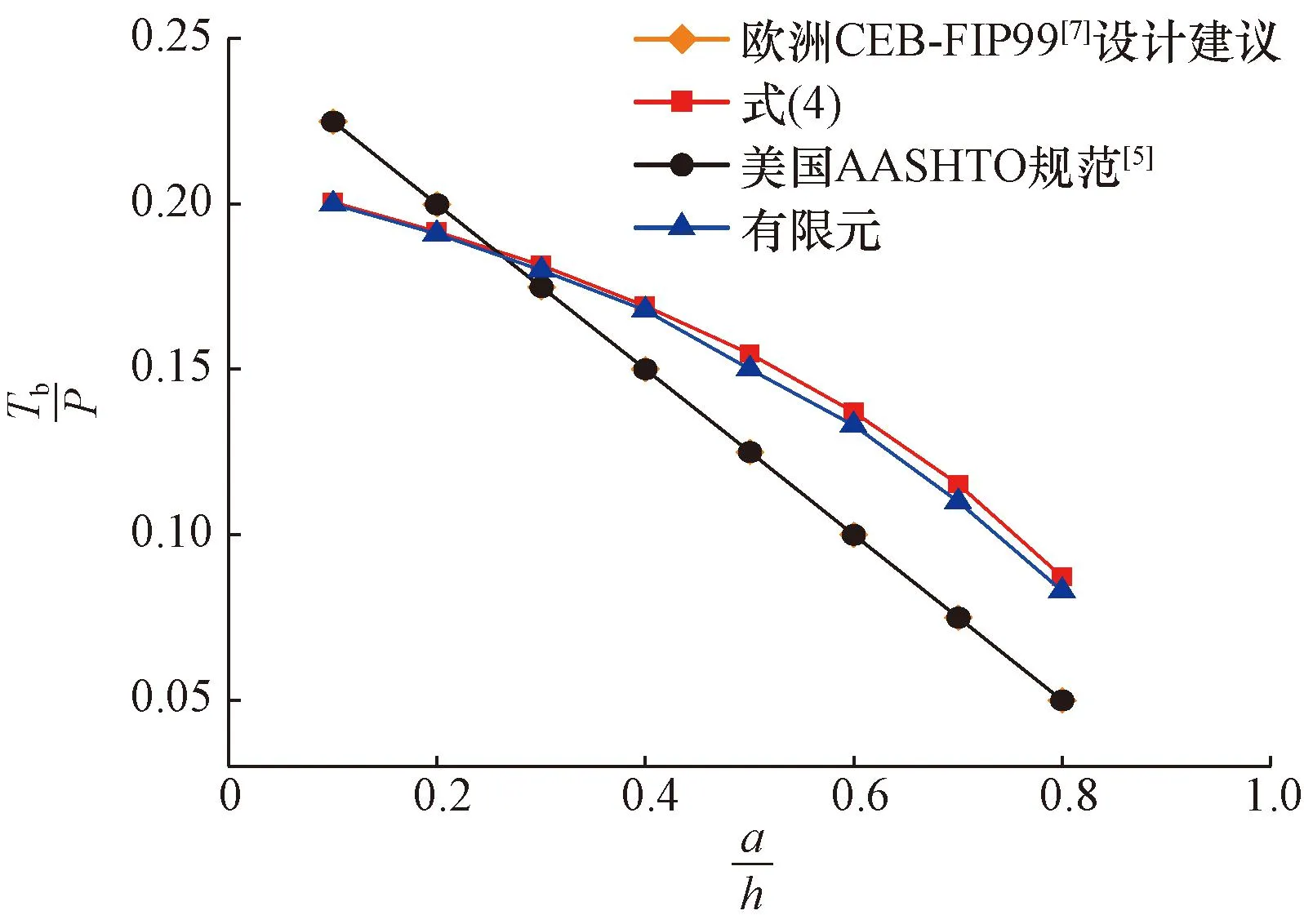
图10 劈裂力大小对比(θ=10°)Fig.10 Comparison of the magnitudes of bursting forces(θ=10°)

(7)径向区横向拉杆与斜压杆之间的夹角取值应尽量偏大,以满足抵抗上方混凝土受拉开裂以及横向拉杆与上部边缘最小保护层要求。《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[8]中给出径向力引起的拉力为

(5)

2 焊接锚垫板锚固区配筋计算

拉压杆模型是锚下力流传递的简化模型,基于拉压杆模型的分析是一种弹性阶段下的应力分析,是结构配筋设计的基础。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[8],对于持久设计状态,结构配筋应满足承载能力极限状态进行设计。

γ0Sd≤Rd

(6)

式(6)中:γ0为桥梁结构重要性系数,取值与安全等级有关;Sd为承载能力极限状态下作用组合效应设计值;Rd为结构构件抗力设计值。

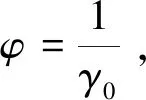
γ0T≤fyAs

(7)

式(7)中:T为受拉部位拉力设计值;fy为钢筋屈服强度;As为受拉钢筋配筋面积。

3 算例

某预应力连续梁齿板锚固区尺寸如图11所示,其中,抗裂钢筋采用HRB335级钢筋,预应力钢束采用9φj15.24钢绞线,锚垫板使用9孔焊接锚垫板,钢绞线抗拉强度fpk=1 860 MPa。

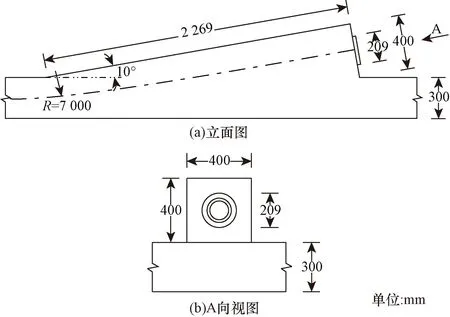
R为预应力孔道曲率半径图11 齿板尺寸Fig.11 Blisters size

根据所确定的焊接锚垫板下拉压杆模型,对齿板结构进行配筋设计。受拉钢筋抗拉强度设计值fy=300 N/mm2,保护层厚度αs=40 mm,钢绞线公称截面积A=9×140=1 260 mm2,单根钢绞线张拉控制应力σcon=0.75fpk=0.75×1 860=1 395 MPa,控制张拉力设计F=1.2σconA=2 109 kN。焊接锚垫板齿板锚固区具体布筋方式阐述如下。

(1)对拉压杆模型施加单位力,采用桁架内力计算方法确定拉压杆模型各拉杆的内力,如图12所示。

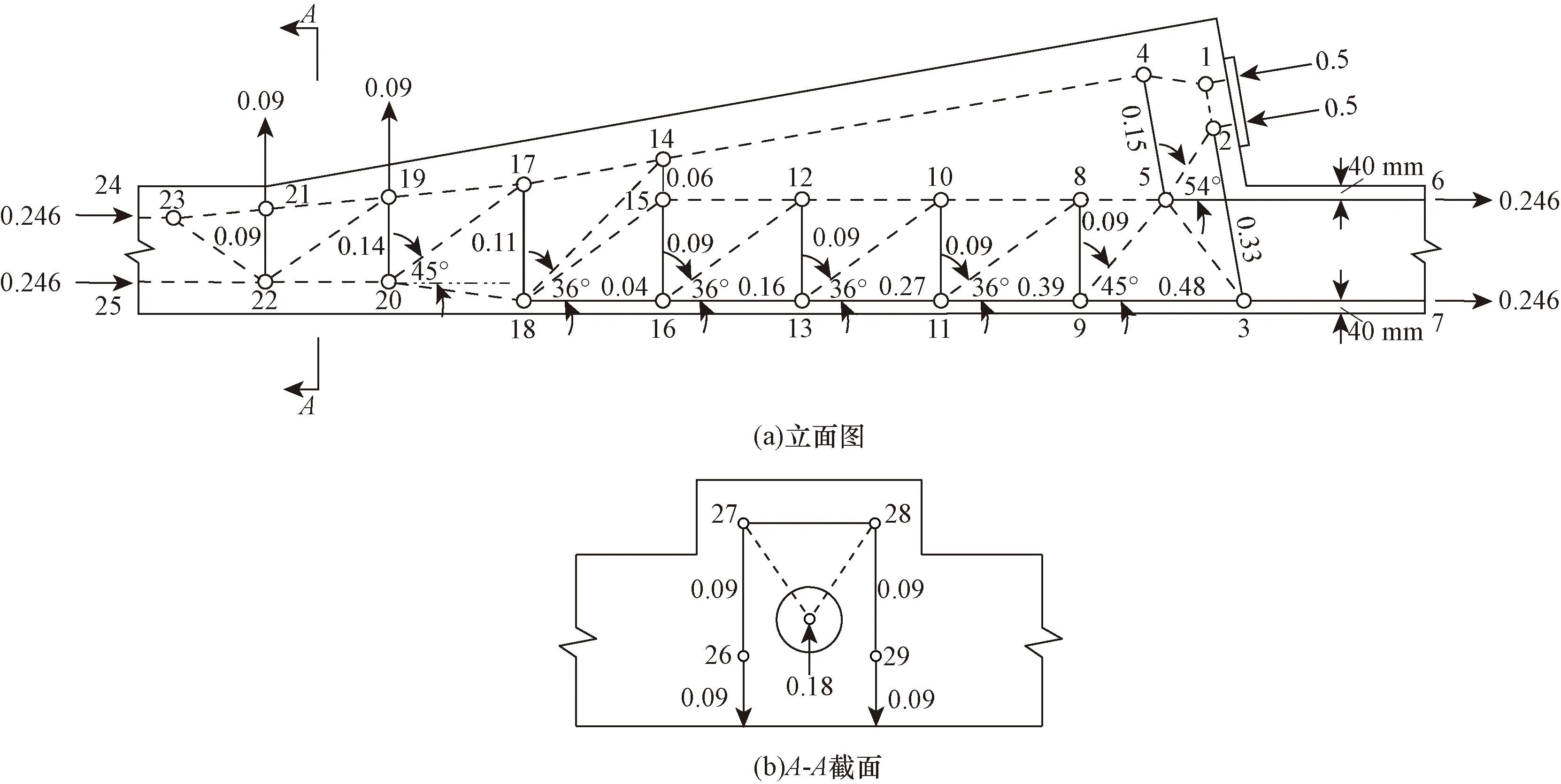
0.5、0.246和0.09分别为外荷载、结构反力和拉杆所受内力,无量纲图12 拉压杆模型及荷载分配比例Fig.12 Strut-and-tie model and Load distribution ratio

(2)通过拉压杆模型计算各典型效应所对应的计算配筋量,与《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[8]以及美国ACI 318-19规范[6]计算配筋量进行对比,如表4所示。按本文拉压杆模型所计算的抗力设计值大于《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[8]计算的抗力设计值,拉压杆模型计算抗力设计值比美国ACI 318-19规范[6]计算的抗力设计值更经济,因此,将所设计的拉压杆模型用于配筋计算更经济和安全。

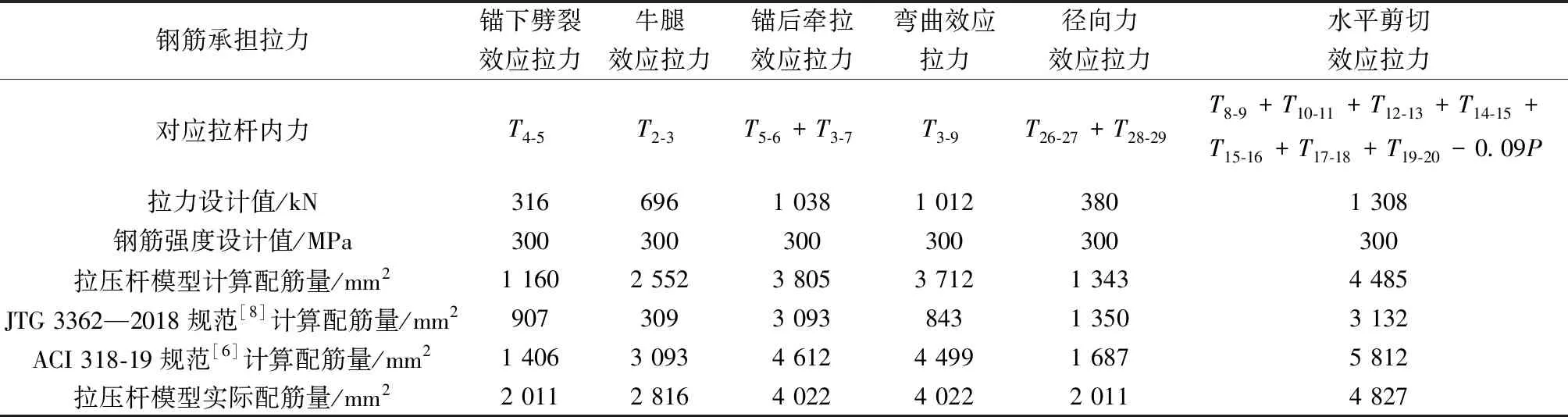
表4 配筋量计算Table 4 Reinforcement calculation

(3)进行锚固区重要部位抗裂配筋时,为得到裂缝的有效控制,需保证配筋重心与拉杆重合。由此抵抗劈裂效应的钢筋需在距离锚固端2db范围内均匀配置;由于劈裂效应配筋和牛腿效应配筋在同一区域,可在每层钢筋网片增加2肢用于抵抗牛腿效应产生的拉力;为使锚后牵拉效应配筋布置合理,由平面应力迹线可知,锚后牵拉作用沿纵向逐渐趋于均匀,沿横向逐渐衰减,将配筋均匀布置在底板上下缘及横向一倍齿板截面宽度以内;弯曲效应所需配筋与锚后牵拉效应配筋有部分重叠,可采用二层布置用于抵抗弯曲效应引起的拉力。相应的钢筋布置情况,如图13所示。

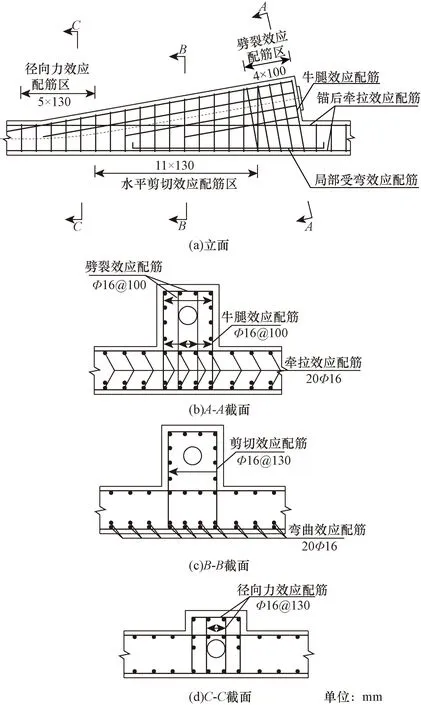
图13 钢筋布置Fig.13 Reinforcement arrangement

4 结论

关于齿板锚固区设计方法,各国规范设计方法都是根据试验数据统计回归得到,配筋往往通过经验进行估算,对于焊接锚垫板齿板锚固区,经验公式不够精确和安全。根据不同国家规范并结合齿板锚固区应力分布规律和有限元分析,提出了适用于焊接锚垫板齿板锚固区的拉压杆模型设计方法,通过算例分析进行锚固区抗裂钢筋布置,得出如下主要结论。

(1)通过齿板锚固区应力分布和应力迹线分析,在弹性受力阶段,齿板锚固区内由锚前受压和锚后牵拉扩散的力均为50%。

(2)提出了一种针对于焊接锚垫板齿板锚固区的拉压杆模型,该拉压杆模型能够真实反映锚固区内力流传递规律;研究了拉压杆模型基本构形的定量化确定方法;所提出的焊接锚垫板锚下劈裂力合力重心计算公式和劈裂力公式,与各国规范给出的公式比较计算精度更高。

(3)通过算例分析,所建立的拉压杆模型具有良好的实用性,以此布置锚下抗裂钢筋,具有足够的强度储备,锚固区设计能较好满足要求。

该类焊接锚垫板已经在一些工程中得到了应用,如北京市政路桥公司在北京轨道交通新机场线一期工程项目中,使用了YJM15-5、YJM15-6焊接锚垫板;江西路桥建设公司在湖南省郴州市安仁县S901线的安仁大桥拆除重建项目工程中,使用YJM15-12焊接锚垫板。在使用过程中用户反映产品性能满足要求,具有推广价值。