基于决策树的自适应互补滤波姿态解算

李瑞, 王伟, 唐龙鑫, 李洁

(1.重庆邮电大学自动化学院, 重庆 400065; 2.重庆市医用电子与信息技术工程研究中心, 重庆 400065;3.重庆邮电大学生物信息学院, 重庆 400065)

高精度姿态信息对无人机、人体运动姿态分析和导航定位后期分析起着决定性的作用。然而,在姿态和位移的估算中,存在着估算精度低、易受磁场和大加速度干扰问题。

目前,常用的3种基础姿态解算算法有梯度下降算法、卡尔曼滤波算法、互补滤波算法[1-3]。中外学者为提高姿态解算精度和抗干扰能力,基于上述3种基础算法提出很多改进方法。高怡等[4]使用梯度下降法来解算姿态信息,通过引入自适应因子和常量控制因子来增强算法在复杂环境下的自适应能力,从提高解算精度。但是从结果来看,精度提升有限,而且并未考虑磁场和加速度的干扰问题。卢艳军等[5]通过两次扩展卡尔曼的方法来改进常规的卡尔曼滤波算法,实验证明在静态和动态下的姿态精度都得到改善,具有一定抗磁干扰性质。但是在静态测试中,还是不能完全隔绝磁场干扰,偏航角存在较大误差。Li等[6]在互补滤波算法中引入两个独立的参数和来分别抵抗加速度干扰和磁场干扰,但单纯的引入并不能有效的解决复杂环境对姿态的影响。

鉴于此,提出一种基于决策树的自适应互补滤波姿态解算方法,通过综合加速度干扰和磁场干扰的程度来自主调节合适的系统误差增益参数,以避免外部干扰对姿态解算精度的影响。

1 姿态系统概述

根据惯性导航原理,一般定义两个基本坐标系,分别为导航坐标系n和载体坐标系b,如图1所示。其中,导航坐标系Xn-Yn-Zn轴指向东-北-天方向,载体坐标系Xb-Yb-Zb轴构成右手直角坐标系。惯性传感器的姿态就是载体坐标系b相对于导航坐标系n的三维方向关系[7]。姿态表达方式有欧拉角、四元数和旋转矩阵3种。因四元数有着独特的优势,主流的姿态算法主要基于四元数法进行姿态估算,只有在表示最终估算结果时,将四元数转换为易于理解的欧拉角。

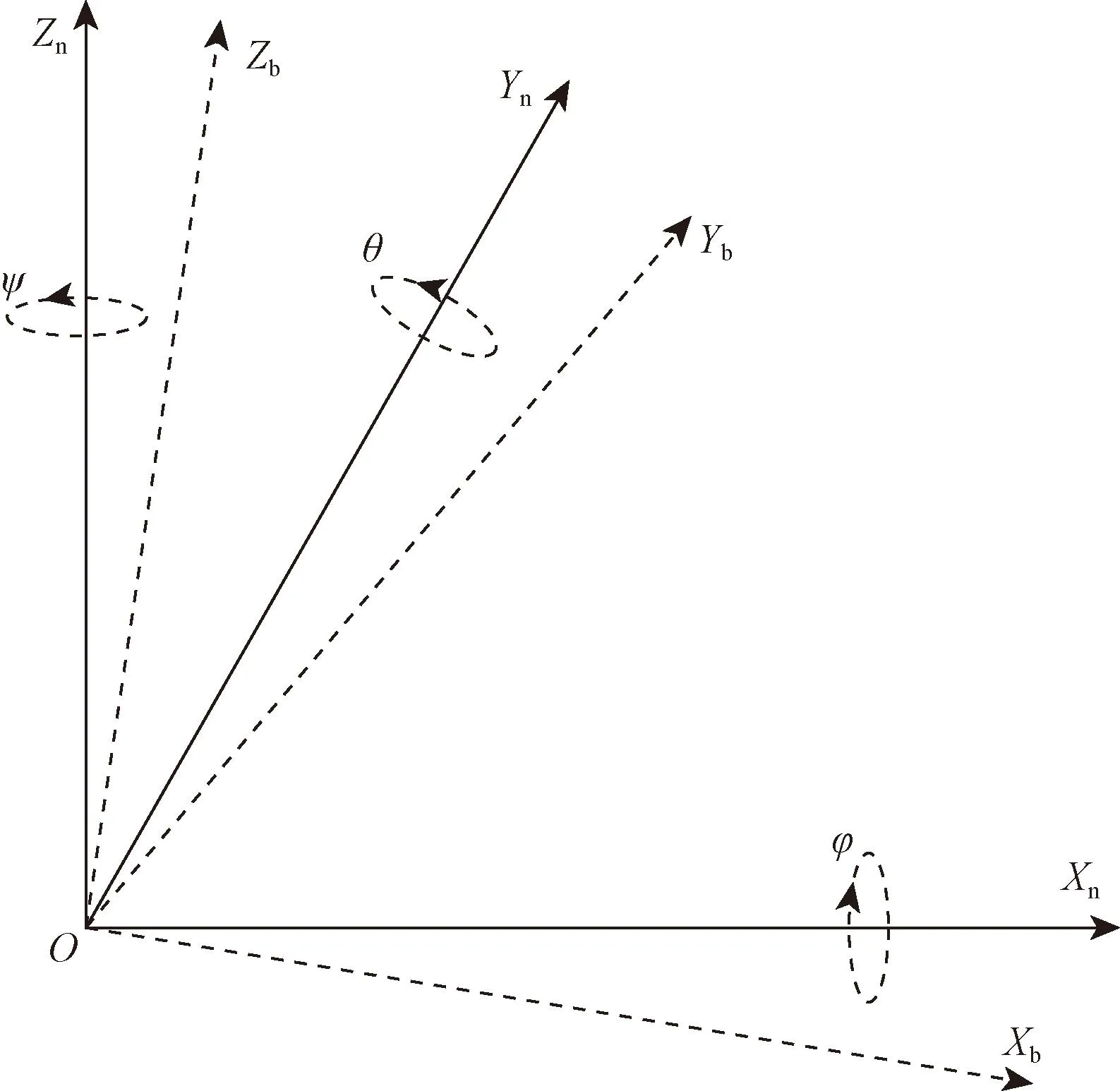
Xn-Yn-Zn为导航坐标系;Xb-Yb-Zb为载体坐标系;ο为坐标原点;φ为俯仰角;θ为横滚角;ψ为航向角图1 导航坐标系和载体坐标系Fig.1 Navigation coordinate system and carrier coordinate system

2 基于决策树的互补滤波算法设计

2.1 算法框架

算法系统框架如图2所示。首先,将零偏补偿的角速度数据和原始加速度数据构成静态检测单元,判断姿态是否发生变化,如果判断为静态,姿态信息就用上一刻的姿态更新;判断为动态,就利用磁场数据和加速度数据来构成决策树,决策树能够根据干扰程度自适应的调节误差增益进而达到抵抗外界干扰。将加速度误差和磁场误差相加,乘上互补滤波的比例调节系数,再与角速度相加,就可以得到修改后精准的角速度数据。然后四元数的变化率就可以通过上一刻的姿态信息和角速度数据得到,最后通过积分更新四元数表示的姿态并进行四元数归一化,得到新的姿态信息。

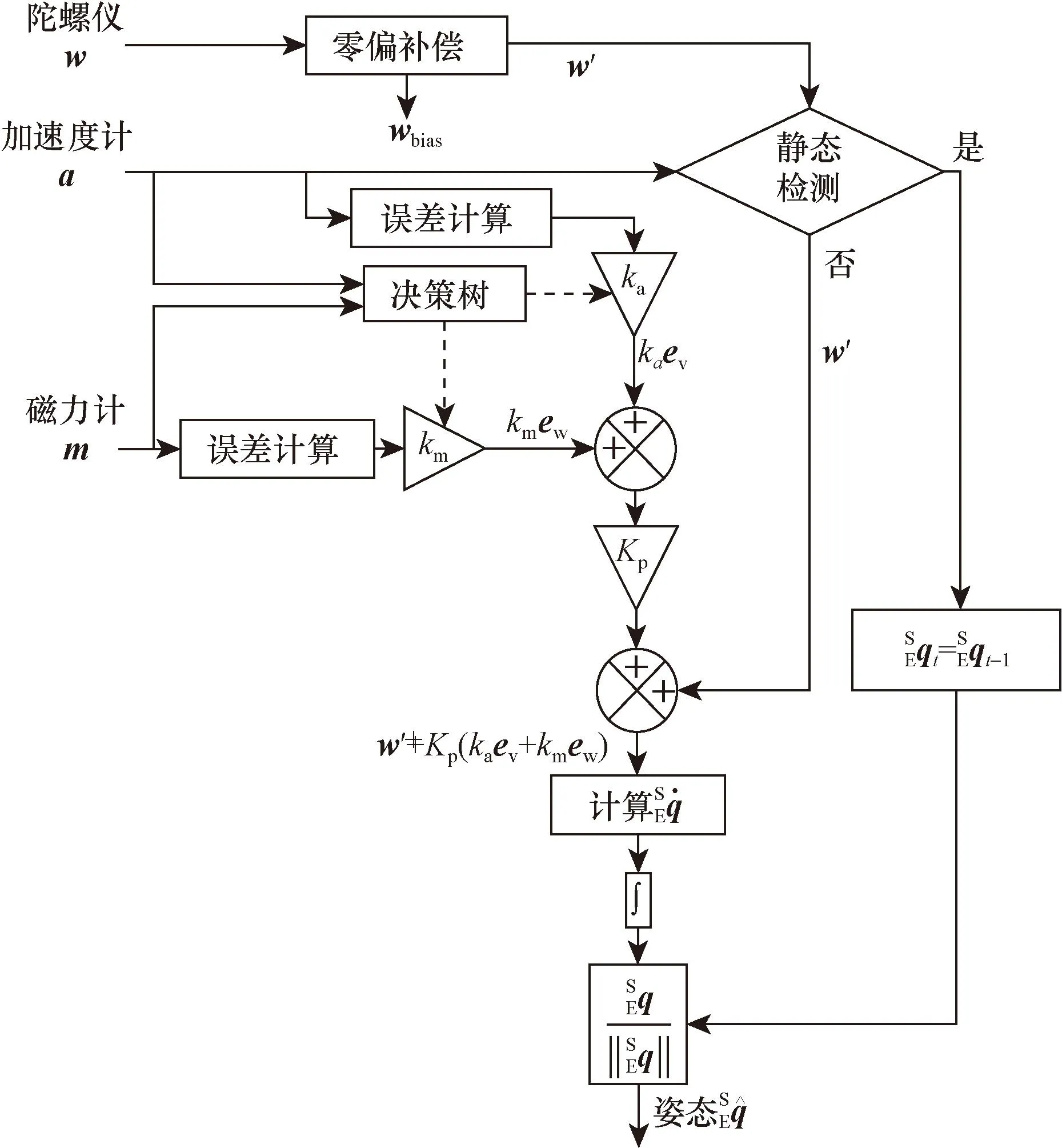
w为单位为rad的处理后角速度;a为加速度;m为磁力计矩阵;wbias为零偏矩阵;w′为零偏处理后角速度;ka为加速度增益;km为磁场增益;ew为磁场误差矩阵;ev为加速度误差矩阵;Kp为比例调节系数;为四元数变化率;为更新后姿态;为更新后姿态;为归一化后姿态图2 系统算法流程Fig.2 System algorithm flow

2.2 静态检测单元

惯性传感器处于静止时,偏航角最终会收敛到地磁场方向。如果没有分辨静态和动态状态,处于静止的传感器在受磁场干扰的环境下,不可避免地会造成偏航角误差。所以当传感器处于静止时,最好的办法就是保持当前的姿态不变,这样就可以抵抗外界磁场带来的干扰。

2.2.1 陀螺仪零偏估计

陀螺仪零偏是影响角速度精度的重要因素之一,它会随温度、时间而改变,无法在出场标定时校正,需在使用过程中修正[8]。

考虑到陀螺仪的零偏是一个缓变的信号,可将零偏看作低频的噪声并通过低通滤波的方式进行估算。为了避免滤掉有用的信息,仅在惯性传感器发生微小抖动时进行。可以认为在一定的时间范围内,微小抖动时间越长,零偏值越大。

改进低通滤波法表示为

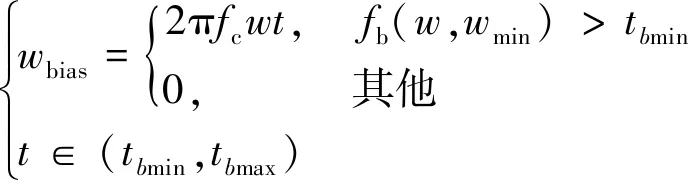
(1)

式(1)中:wbias为零偏估计值;fc为截止频率;t为时间;w为角速度原始数据;t为时间;函数fb(w,wmin)的功能是统计角速度w小于wmin的时间,其中,wmin为设定的静态判断阈值;tbmin和tbmax分别为最小、最大静态时间。

实际应用中,物体不可能绝对静止,一些细微抖动会让陀螺仪不可避免的产生偏移,而按照上述方法,可有效去除细小抖动。如图3所示。

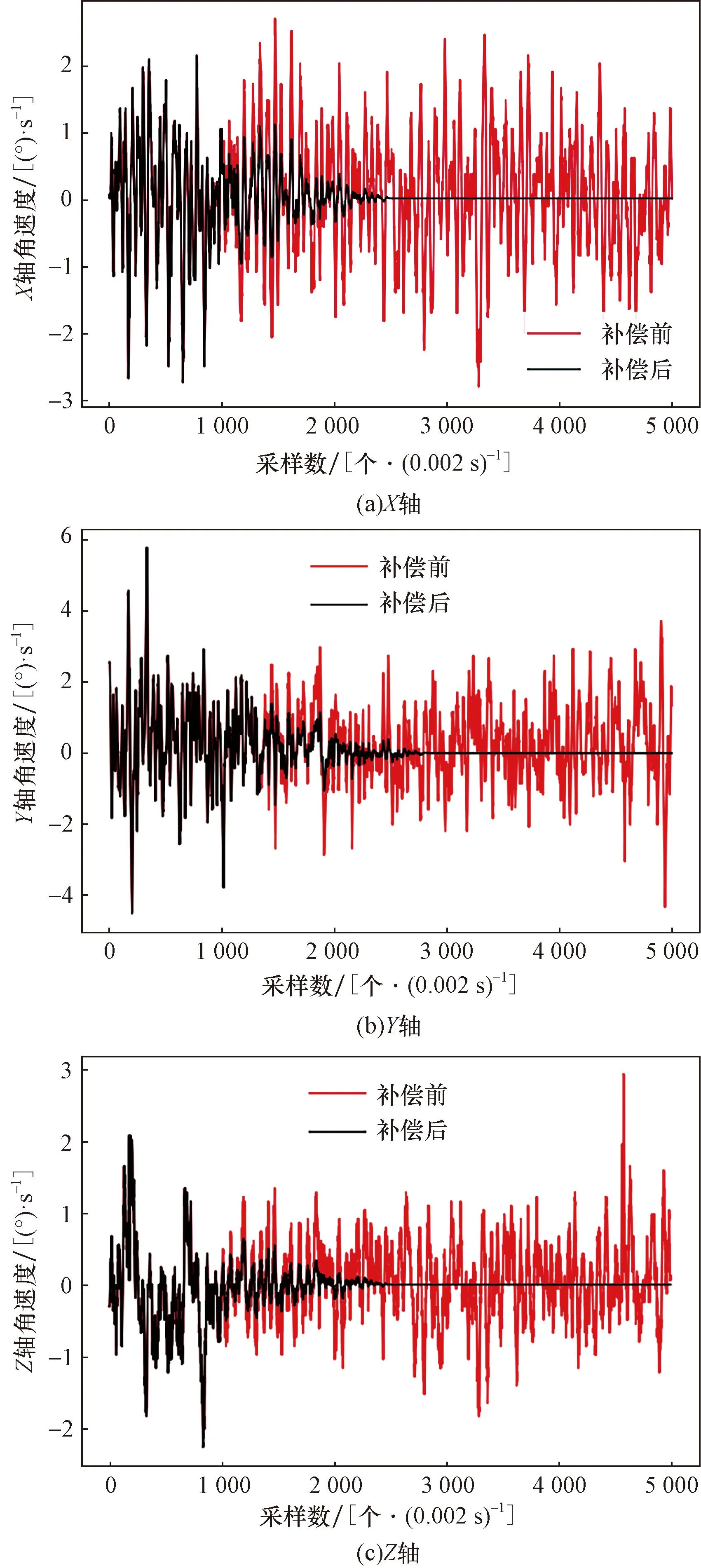
图3 三轴陀螺仪零偏补偿Fig.3 Three-axis gyroscope zero compensation

2.2.2 静态检测

加速度数据和陀螺仪数据均可用于静态检测,但最好用两种数据融合做判断,这样判断会更加精准[9]。通过给角速度和加速度变化值设置阈值的方法来共同判断传感器当前的状态,判定的准则分为加速度判定和角速度判定。

基于陀螺仪的静态准则有

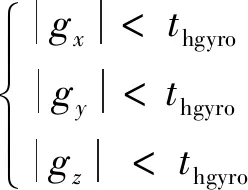
(2)

式(2)中:thgyro为设定的角速度阈值;gx、gy和gz为三轴角速度测量值。

当陀螺仪任一轴的绝对值超过设定的阈值时,则处于动态;反之如果连续检测100次,一直满足静态准则,则处于角速度静止状态。

基于加速度计的静态准则有

(3)

式(3)中:axt、ayt、azt分别为t时刻X轴加速度测量值;axt-1、ayt-1、azt-1为t-1时刻X轴的加速度测量值;thacc为加速度阈值。

当加速度计任一轴的此刻输出值减去上一刻输出值的差值的绝对值超过阈值时,处于动态;反之如果连续检测100次,一直满足静态准则,则处于加速度静止状态。

当同时满足角速度检测静止和加速度检测静止时,系统处于静态,反之处于动态,如图4所示。

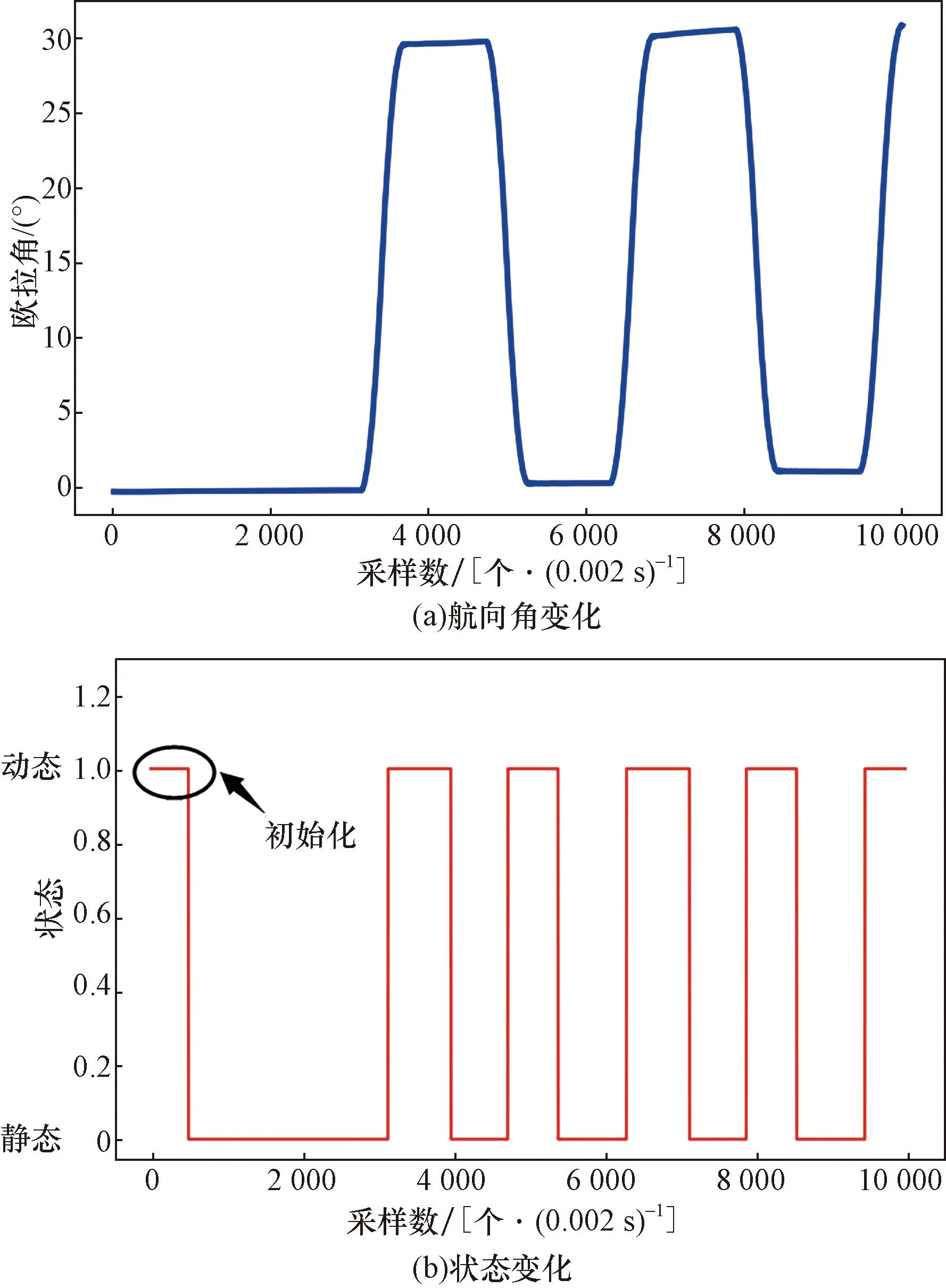
图4 静态检测图Fig.4 Static detection map

2.3 互补滤波

姿态解算从理论上讲只用陀螺仪就可以实现,但由于陀螺仪在积分过程中会产生累计误差。如果没有外力干涉,解算可信度将会越来越低,故需要加速度计对重力进行比对和补偿,用来修正陀螺仪的垂直误差。对于竖直轴上的旋转,加速度计是无能为力的,此时就需要磁力计测量水平面的地磁方向来修正陀螺仪的水平误差。而互补滤波法就是根据传感器的特性不同,取长补短,融合数据得到更加准确的姿态。

已知在导航坐标系中,重力加速度G可表示为

G=[0,0,1]

(4)

加速度预测值as的计算公式为

(5)

式(5)中:vx、vy、vz分别为三轴加速度预测值;q0、q1、q2、q3为组成四元数的四位数,其中,q0是标量,q1、q2、q3是矢量。

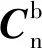
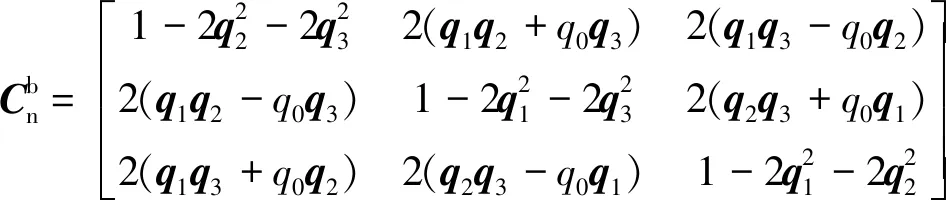
(6)

因为加速度计的测量值ab=[ax,ay,az]与预测值as存在误差,故通过向量叉乘可得加速度误差ev,可表示为

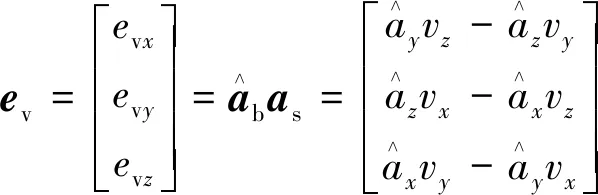
(7)

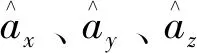
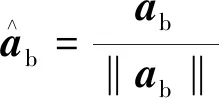
(8)

同理,磁力计在导航坐标系的参考方向为[bx, 0,bz],地球上不同地方的磁场方向和大小均不一致,故bx和bz为未知量。但是可以使用磁力计测量值来模拟当地的磁场,步骤如下。

首先,设地磁场的值为

h=[hx,hy,hz]T

(9)

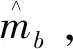
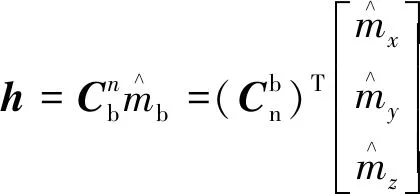
(10)

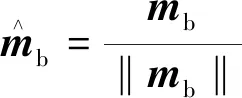
(11)

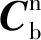
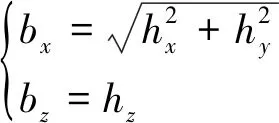
(12)

式(12)中:hx、hy、hz分别为通过磁力计计算的地磁场在导航坐标系下的三轴分量;bx为水平面上的地磁;bz为垂直面上的地磁。

则磁场的预测值ms可表示为

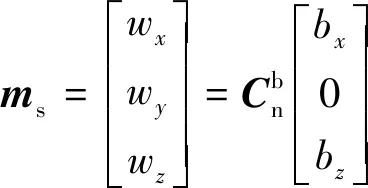
(13)

根据磁力计的测量值与预测的误差,同样通过向量叉乘得到磁场误差ew,可表示为

(14)

陀螺仪的原始测量值w的单位为(°)/s,因此需要将测量值转化为单位为rad的值,可表示为

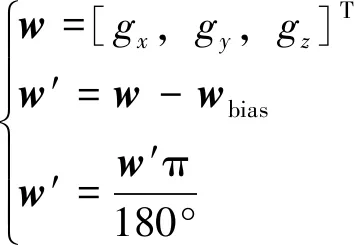
(15)

然后将加速度误差和磁场误差来加入原始角速度中,得到修正后的角速度w″为

w″=w′+Kp(kaev+kmew)

(16)

式(16)中:Kp为比例调节系数;ka和km分别为加速度增益和磁场增益。

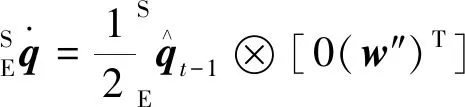
(17)

四元数乘法的具体表达式为

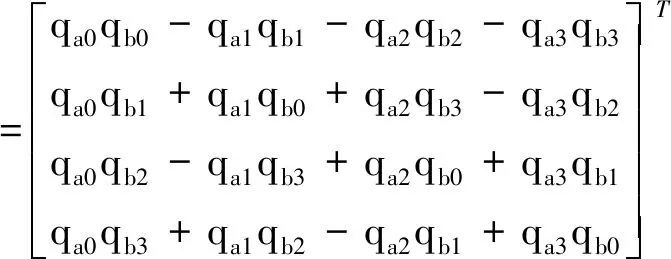
(18)

然后通过积分更新姿态信息,并且归一化有

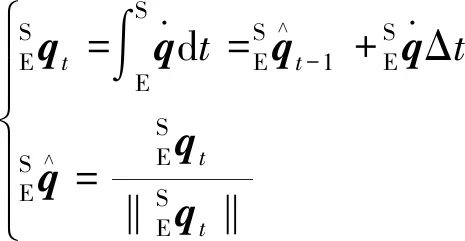
(19)

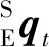
最后,四元数表示的姿态转化为欧拉角[10],欧拉角包含绕x轴的俯仰角Pitch、绕y轴的横滚角Roll和绕z轴的偏航角Yaw,其转换公式为

(20)

2.4 决策树

决策树是一种属于监督学习的分类方法。在本决策树中主要分为两大部分,分别为加速度干扰检测部分和磁场干扰检测部分。

根据加速度干扰特性,将加速度干扰分为3种类型:弱加速度干扰、弱加速度干扰超时、强加速度干扰,主要采用加速度幅值‖a‖和加速度干扰计时器atime来判定。

(21)

由于磁力计的敏感性,磁场数据非常容易受到外界干扰,将磁场干扰分为4个类型:弱磁干扰、弱磁干扰超时、强磁干扰和强磁干扰超时。在过往的抗磁研究中,普遍检测磁场的参数会选用磁场强度和磁倾角[11],但在不同的地方,地磁场的差异会导致磁场强度的标准发生变化,故导致磁场强度和磁倾角发生偏差,系统就会错误的判断为产生了磁场干扰,影响算法的精准性。本文算法将陀螺仪引入,选用磁力计计算的偏航角和陀螺仪计算的偏航角之差dpsi和磁场干扰计时器mtime作为判定原则来判断是否发生磁场干扰,增加了判定干扰的准确性,其表达式为

(22)

将4个参数用来共同构成决策树,如图5所示,首先,分别判断dpsi和‖a‖是否属于设定的(thm1,thm2)和(tha1,tha2)阈值区间内,其中,thm1为弱磁左界限,thm2为弱磁右界限,tha1为弱加速度左界限,tha2为弱加速度右界限。再判断其时间是否超过时间阈值thtime。最后得到加速度干扰的3种状态和磁力干扰的4种状态,将之两两组合,一共可以得到12种组合。将12种状态分配出不同的km和ka两种误差增益应对不同的干扰。

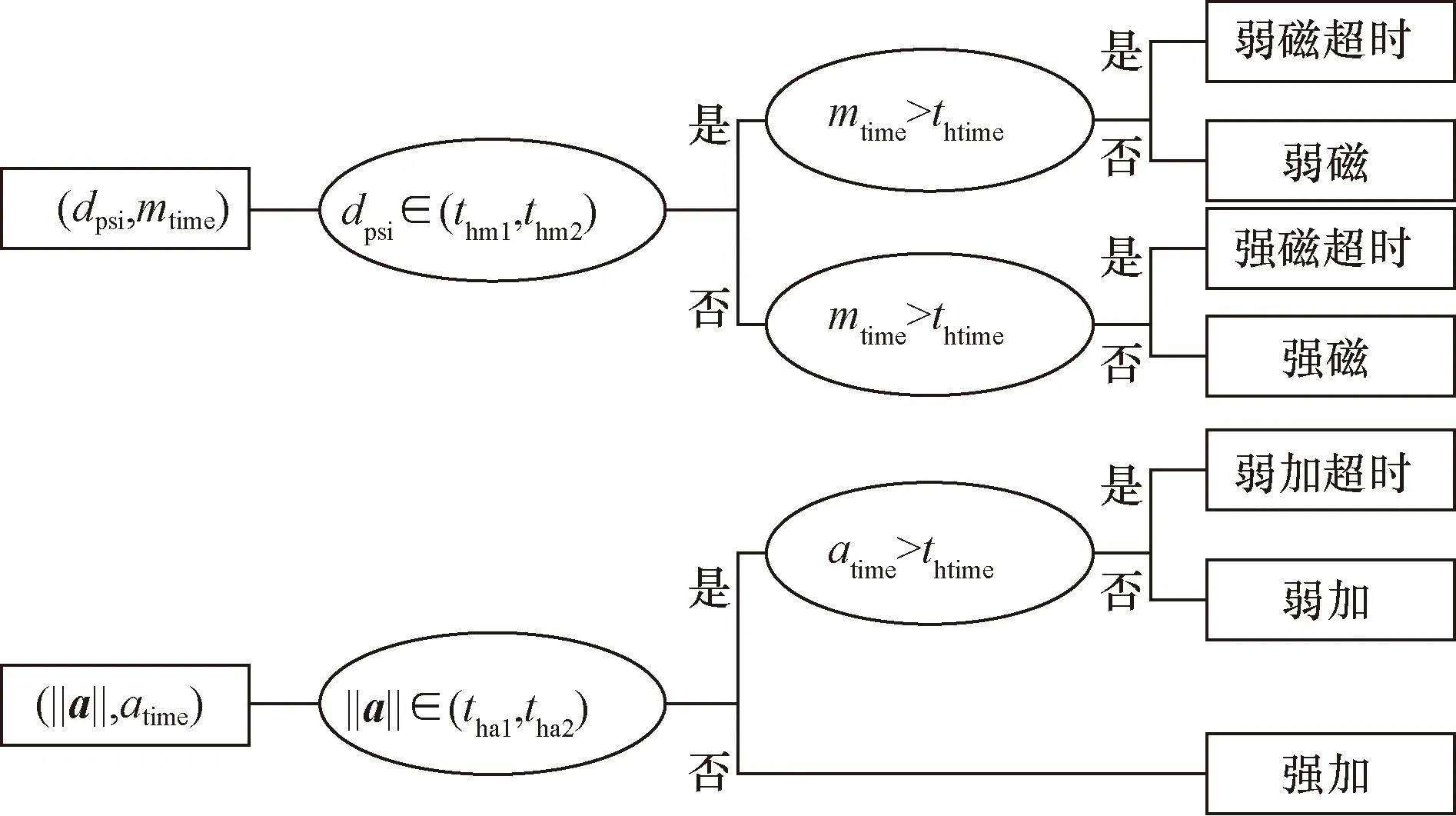
dpsi为磁力计和陀螺仪计算的偏航角之差;‖a‖为加速度幅值;atime为加速度干扰时间;mtime为磁干扰时间;(tha1,tha2)为弱加范围;(thm1,thm2)为弱磁范围;thtime为时间阈值图5 决策树逻辑Fig.5 Decision tree logic

3 实验系统设计和结果分析

3.1 硬件系统和算法参数

本系统主要核心控制器为STM32F407,惯性传感器为维特JY931,它包含了三轴加速度计(量程为±16g,g为重力加速度)、三轴陀螺仪[量程±2 000°/s]和三轴磁力计。整个硬件系统如图6所示。

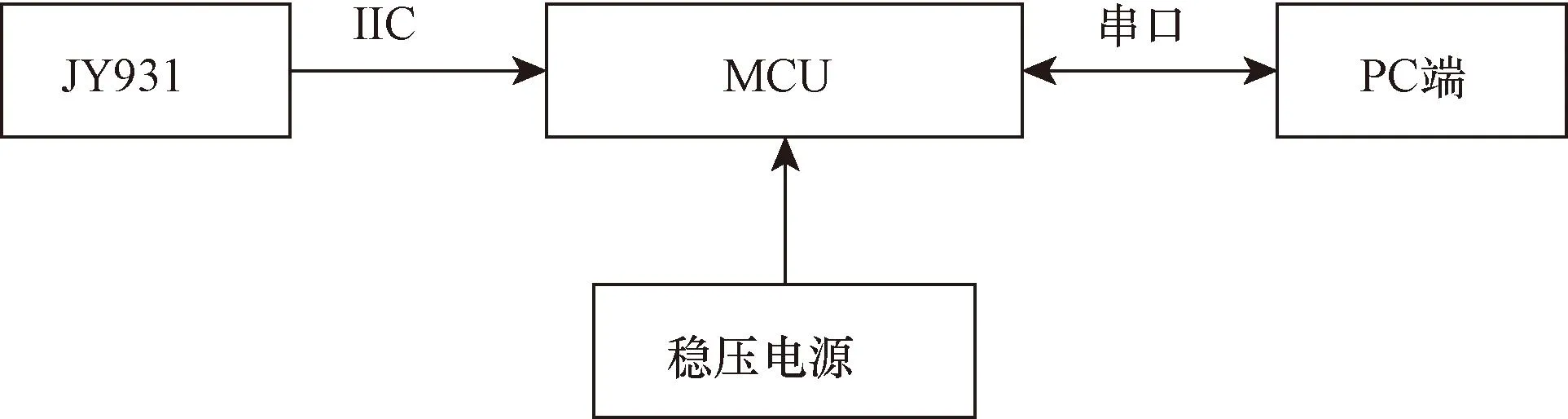
MCU为微控制单元;IIC为集成电路总线;JY931为惯性传感器;PC为个人电脑图6 硬件系统Fig.6 Hardware system

本系统惯性传感器采样率为500 Hz,低通滤波参数设置截止频率fc=0.019 894Hz;最小静态时间tbmin=1 s;最大静态时间tbmax=8 s;静态判断阈值wmin=(5, 5, 3)。静态检测参数设置:角速度阈值thgyro=2°/s;加速度阈值thacc=0.025 m/s2;比例调节系数Kp=1。

3.2 无外部磁体干扰测试

本实验主要测试本文方法的可行性和优越性。实验平台如图7(d)所示,实验具体步骤如下:将惯性传感器水平的固定在旋转机械臂上,机械臂通过电脑(PC)端精准控制其旋转角度,分别采取20、60、120 s时长的运动数据,每个实验重复5次。最后比较九轴梯度下降算法(gradient descent algorithm,GDA)、改进的显式互补滤波算法(improved explicit complementary filtering,IECF)、无静态检测的决策树互补滤波算法(decision tree complementary filtering without static,DTWS)、双线性卡尔曼滤波算法(double linear kalman filter algorithm,DLKF)[12-13]和本文算法估算姿态欧拉角均方根误差的平均值,如表1所示。图7(a)～图7(c)为惯性传感器在20 s内水平旋转0° ～ 30°往返,运动间隔时间为2 s。

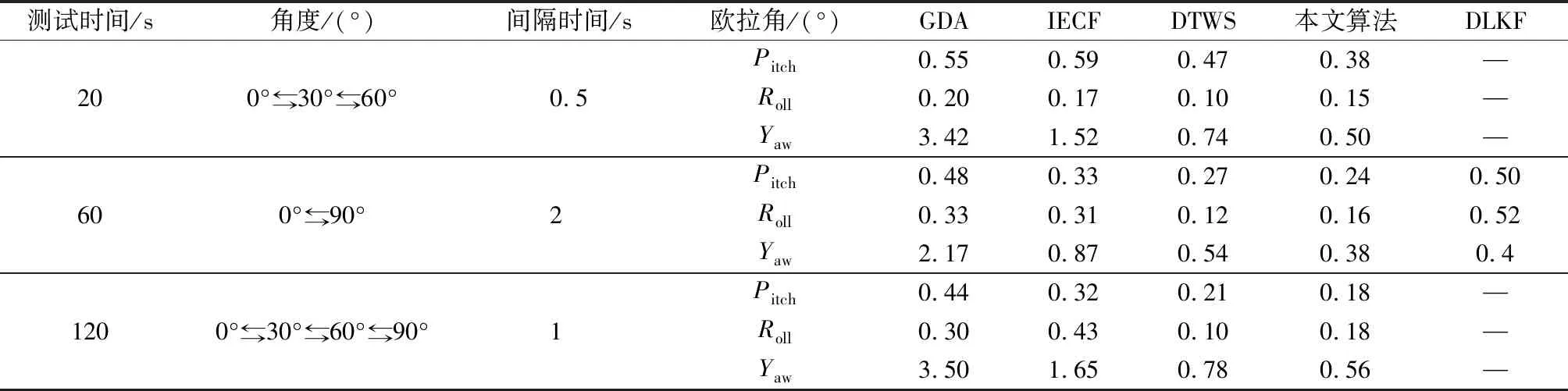
表1 不同算法欧拉角均方根误差的平均值Table 1 Average value of root mean square error of Euler angles for different algorithms

图7 三轴欧拉角和实验平台Fig.7 Three-axis Euler angles and experimental platform

3.3 磁物体干扰测试

本实验是惯性传感器60 s内水平旋转从0°～90°往返,运动间隔时间为2 s。其中,用磁铁进行随机的磁场干扰,从图8(a)中可以看出,实验中出现多次随机的外部磁干扰。结果[图8(b)～图8(d)]显示:本文算法、GDA和IECF的偏航角均方根误差分别为0.96°、3.88°、15.08°,表明本文算法相较于其他两种算法有着抗干扰优势。

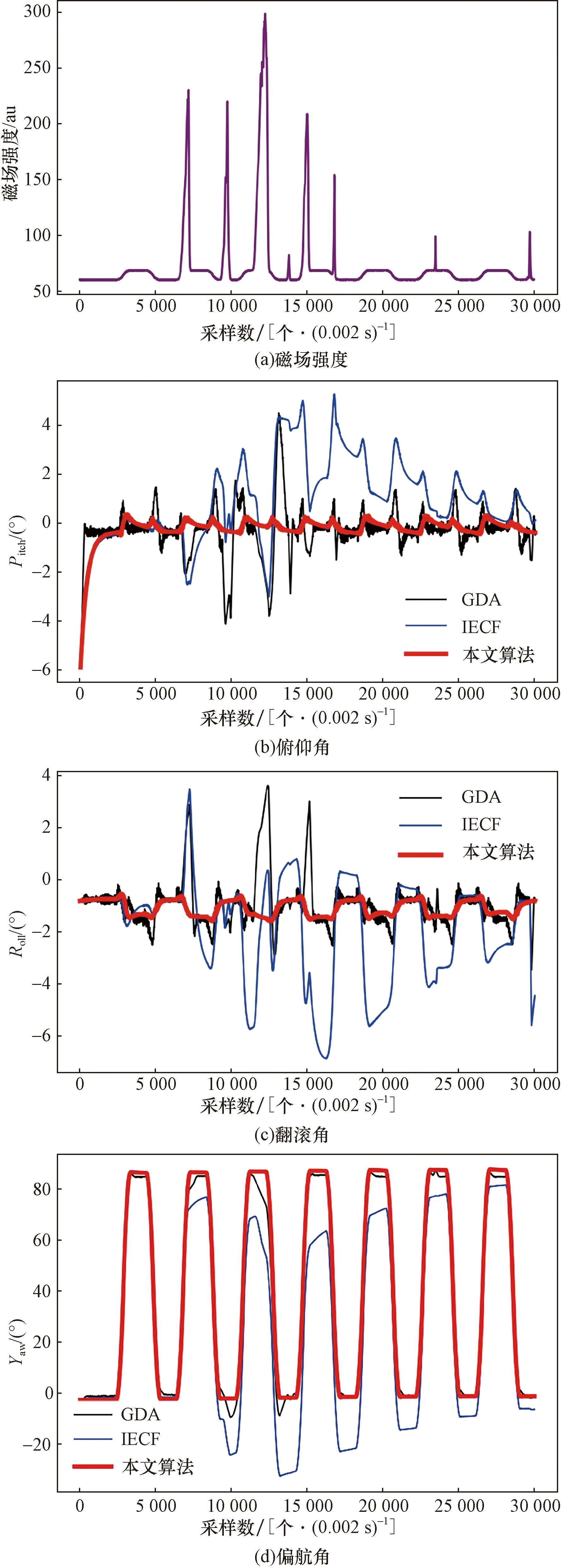
图8 抗磁实验欧拉角Fig.8 Antimagnetic experiment Euler angle

4 结论

加速度干扰是普遍存在且难以回避的,因为加速度干扰伴随着运动而存在,不能完全消除,只能抑制。得出以下结论。

(1)从无带磁物体干扰测试实验结果可以看出,提出的基于决策树的互补滤波算法具有可行性,而且相较于其他算法,抑制加速度干扰能力更强,解算精度更高。

(2) 在外部磁场干扰下,相对于GDA算法,所提算法抗干扰能力提高了75.3%。

解算的精度对于后续的研究有着关键性的作用,此算法将用于后续手势轨迹重构研究中,进一步提高轨迹重构的精度。