基于PSD特征的FBCCA脑电信号识别方法

张学军, 杨京儒

(1.南京邮电大学电子与光学工程学院, 南京 210023; 2.南京邮电大学柔性电子(未来技术)学院, 南京 210023)

脑机接口(brain computer interface,BCI) 是指通过检测大脑活动时产生的脑电波,实现大脑直接与外部设备进行通信和控制,而大脑外周神经和肌肉不参与外部设备的互动[1-2]。BCI系统首先对被试在不同的认知任务下的脑电信号进行相关的特征提取,再对提取出来的特征通过相关的分类器进行分类,最后根据分类的结果生成控制命令,将控制命令发送给被控对象,实现脑控外部设备的功能[3-4]。因此,脑机接口在医疗康复等方面有着重要的应用[5]。除传统的功能恢复和严重运动障碍患者的神经康复领域,BCI系统还被广泛应用于环境控制、运动娱乐和情绪识别[6-7]。而在脑机接口中,低成本、无创伤的头皮脑电(electroencephalogram,EEG)受到研究者们的广泛关注[8]。与其他非侵入性神经成像方法,如功能性近红外光谱、功能性磁共振成像、脑磁图等相比,脑电图具有时间分辨率高、易于获取、成本低等优点[9]。

在基于脑电图的脑机接口研究中,有几种常用的无创电生理信号源可作为脑机接口系统的控制信号,如稳态视觉诱发电位(steady-state visual evoked potential,SSVEP)[10]、皮层慢电位[11]、事件相关同步[12]、P300诱发电位[13]。其中,SSVEP是EEG中最常见的一种神经生理信号,与其他电生理信号源相比,基于SSVEP的BCI具有较高的信息传递率(ITR)、信噪比(SNR)和分类精度[14]。

SSVEP是指当用户在受到按照一定频率(一般大于4 Hz)闪烁的目标刺激时,在用户大脑的枕叶区产生的与刺激频率一致的准周期振荡电平信号。一般基于SSVEP的BCI包含多个命令,每个命令对应一个特定频率的刺激。因此,用户可以通过连续注视不同的目标刺激来输出命令[15]。

在检测和提取SSVEP的特征中,常见的算法有离散傅里叶变换[16]、短时傅里叶变换[17]、功率谱密度分析(power spectral density,PSD)[18]、典型相关分析(canonical correlation analysis,CCA)[19]等,其中CCA具有效率高、信噪比好、实现简单、学科间可变性低、可以使用谐波频率、不需要训练要求等优点[20]。

在标准CCA方法的基础上,近年来提出了一些扩展的CCA的方法,如CCA系数聚类分析、基于单个模板的CCA[21]、多路CCA[22]和滤波器组的典型相关分析(filter bank canonical correlation analysis,FBCCA)等。Lee等[23]发明了一种基于FBCCA的自适应窗口SSVEP分类方法,有效地提高了SSVEP信号的识别准确率。但通过标准CCA和FBCCA进行SSVEP的特征提取与分类时,比较的是一组选定导联的SSVEP信号和参考信号之间的相关性系数,并没有充分利用每个导联的单独特性。

使用PSD分析来进行SSVEP的特征提取虽然能够完整利用单个导联的特性,但是存在噪声影响大,没有利用导联组整体特性,识别准确率低的问题。

为了提高SSVEP特征提取的准确率,充分利用每个导联的单独特性与导联组的整体特性,提出一种基于PSD的FBCCA稳态视觉诱发电位脑电信号识别方法。为验证基于PSD特征的FBCCA脑电信号识别方法的效果,通过采集8名被试的SSVEP脑电信号,对采集到的脑电信号使用基于PSD特征的FBCCA脑电信号识别方法进行分类实验。同时使用PSD、CCA、FBCCA的方法对采集到的脑电信号进行分类处理与比较。基于PSD特征的FBCCA脑电信号识别方法可以提高SSVEP识别的普适性与准确率,为脑机接口系统控制设备的实际应用领域提供了一种新的思路。

1 基于PSD的FBCCA目标识别算法

1.1 信号预处理

采集到的SSVEP信号需要经过预处理来去除噪声,提高后续的分类准确率。因为采集的SSVEP信号刺激频率均处于5～17 Hz,为减少后续分析时谐波分量的丢失,因此首先将采集到信号通过4～90 Hz的带通滤波器进行滤波。同时为了降低系统工作时的工频干扰,将处理过的信号再经过一个50Hz陷波滤波器进行滤波。

1.2 典型相关性分析

CCA 属于多元统计学,能够研究变量对之间的相互关系,通过对变量之间的互协方差矩阵的研究来定量反映两组指标之间的整体相关性。CCA方法是针对两组多维变量信号X、Y,找到一组矢量WX、WY,使得x=XTWX,y=YTWY并且X和Y的相关性最大。而对于WX和WY,存在如式(1)所示的关系。

(1)

式(1)中:ρ为相关性,当ρ取最大值时,即可求得WX和WY的最大典型相关系数。

将CCA应用于SSVEP信号的分析时,一般将X设定为一组多导联的脑电信号,而Y设定为一组对应的参考信号。

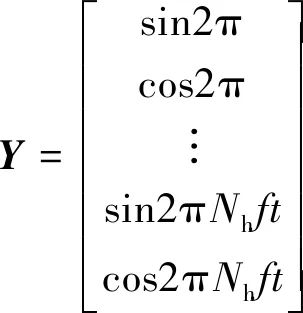
(2)

式(2)中:Nh为谐波数量;f为对应刺激频率;t为时间。

可以通过计算得出多导联脑电信号和参考信号的最大典型相关系数,而最大典型相关系数所对应的频率就是 SSVEP 信号的识别结果。

1.3 滤波器组典型相关分析

FBCCA是针对CCA算法在分析SSVEP信号时会忽略谐波分量而进行改进的算法。FBCCA首先通过具有不同通带的N个带通滤波器对原始脑电信号进行子带分解,滤波器分解出的子带分量为XSBn,其中n为滤波器对应序号,n=1,2,…,N。再对每一个子带分量分别应用标准CCA处理,得到子带分量与所有刺激频率对应的参考信号之间的相关值Yfk,其中,k为参考信号对应序号,最后通过计算得出N个相关值组成的相关向量ρk,可表示为

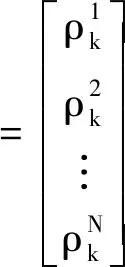
(3)

再通过ρk计算出所有子带相关性系数的加权平方和Wρk,可表示为

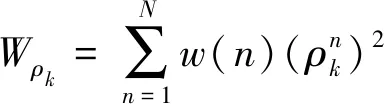
(4)

式(4)中:w(n)为对应子带分量的权值,其中n∈[1N],

w(n)=n-a+b

(5)

式(5)中:a、b为调参系数,当a取1.25,b取0.25时,可以使FBCCA分类准确率达到最大[23]。

对应不同的参考信号k,求出最大的Wρk,其所对应的频率就是 SSVEP 信号的识别结果。

1.4 功率谱密度分析

PSD分析是针对在SSVEP中不同刺激频率使用户产生频率不同的响应的这一特点所设计的。

假定有K个不同频率的刺激信号,它们的刺激频率分别是f1、f2,…,fK。对预处理完的SSVEP信号进行快速傅里叶变换,求取到信号的功率谱密度P(fk),其中k=1,2,…,K。

通过给定频率fk的功率谱密度P(fk)与其n个相邻的频率的功率谱密度的比值计算出SSVEP信号的信噪比SNK(fk),计算公式为

(6)

式(6)中:n的取值为偶数;s为频率分辨率,s=采样率/采样点数;q为中间变量。

将求取出的SNK(fk)进行比较,其中,最大的SNK(fk)对应的频率fk即认定为SSVEP信号的识别结果。

1.5 基于PSD的FBCCA目标识别算法

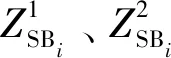
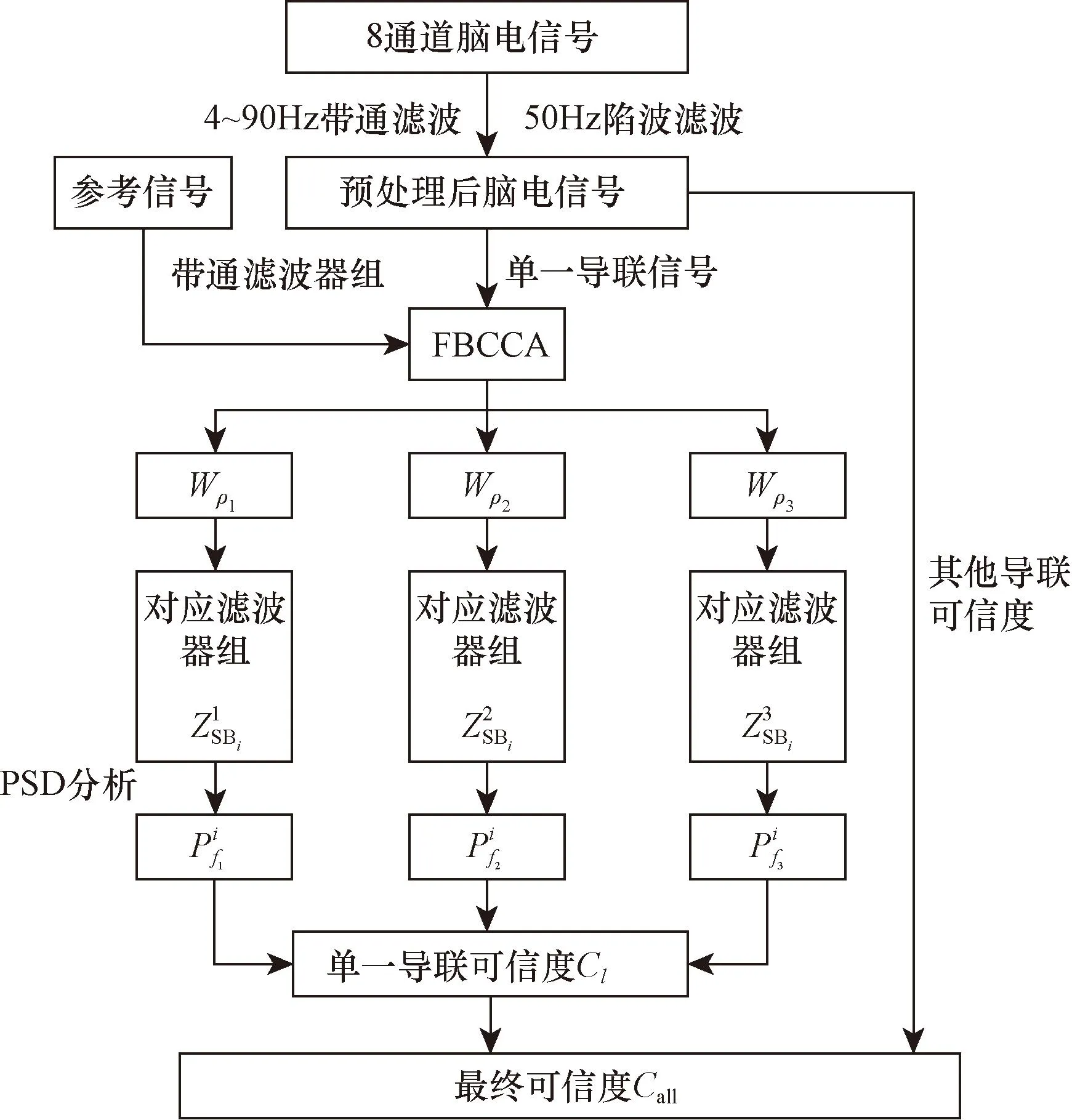
为功率谱密度均值图1 基于PSD的FBCCA的目标识别算法流程图Fig.1 Flow chart of target recognition algorithm of FBCCA based on PSD

步骤1SSVEP脑电信号采集。由于SSVEP响应主要在枕叶视觉区,因此采集O1、OZ、O2、PO3、POZ、PO4、PO5、PO7这8个导联。

步骤2SSVEP脑电信号预处理。将采集到的脑电信号进行预处理,首先将采集到信号通过4～90 Hz的带通滤波器进行滤波。再将处理过的信号再经过一个50 Hz陷波滤波器进行滤波。

步骤3滤波器组进行子带分解。采用的带通滤波器组有9个子频带,其中第n(n=1,2,…,9)个子频带为从[(n-1)10+5] Hz频率开始,到90 Hz结束。在实现带通滤波时,每个子带在通带两侧增加2Hz的额外带宽。将经过预处理的SSVEP脑电信号放入滤波器组进行子带分解。

步骤4FBCCA分析。根据刺激频率设置参考信号,参考信号的谐波数量设置为90/f取整。通过式(4)计算出信号与参考信号的所有子带相关性系数的加权平方和Wρk,再根据对应不同参考信号的Wρk进行大小排序,找出最大的3个Wρk对应的参考信号频率f1、f2、f3,并记录下它们Wρk为Wρ1、Wρ2、Wρ3。

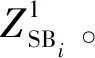
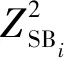
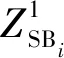
(7)

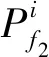
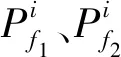
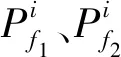
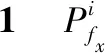
表对应可信度Cl增值的对比结果Table 1 Comparison results of to the increase of credibility Cl

2 实验数据

2.1 实验范式设计

实验采用黑白色块翻转的稳态视觉刺激诱发范式。利用E-prime实现,分辨率为 1 920×1 080 像素,刷新率为144 Hz的显示器作为输出。屏幕背景为白色,刺激色块大小为300×300像素。在每次刺激开始前,为受试者提供注视点,并给予受试者足够的休息时间。

当受试者准备完成后,由受试者主动按下键盘。为了防止受试者肢体移动所带来的肌电影响,在受试者按下按键后,系统会在之后5～10 s后的随机时间段里,在注视点处放出刺激色块。刺激色块的闪烁频率为5、6、7、8、9、11、13、17 Hz随机出现。在一轮刺激中,每种刺激频率均会出现5次,一共给予受试者40次刺激,每次刺激时长为5 s。在一次刺激结束后,为防止受试者出现视觉疲劳等情况,系统将进入为受试者提供注视点的界面。等待受试者准备完成,按下按键后再进入下次的刺激阶段。

实验共招募8名视力或是矫正视力正常的健康被试(S1～S8)。被试者的年龄均处于22～24岁。每名被试在接收实验时均保证睡眠充足,精神状态良好。实验开展时,保证处于安静的环境。被试需要在实验进行过程中保持舒适坐姿,与显示器保持0.5～1 m的距离。实验场景如图2所示。

图2 实验场景Fig.2 Experimental scene

在采集SSVEP信号时,要求被试尽量保持平静并减少眨眼、咀嚼等肌肉运动活动。每名受试者进行两轮实验,每轮实验间为受试者提供至少1 h的休息时间,直到受试者得到充分的休息为止。

2.2 信号采集

实验采用Neuroscan公司生产的脑电64-256导脑电采集系统,电极帽采用Neuroscan的Quik-Cap64导电极帽。信号采样率设定为1 kHz,电极分布按照国际标准的10-20电极安放法放置,电极编号如图3中字母与数字所示。实验一共采集枕叶区的O1、OZ、O2、PO3、POZ、PO4、PO5、PO6这8个导联的脑电信号。采集导联分布如图3中椭圆圈出部分所示。

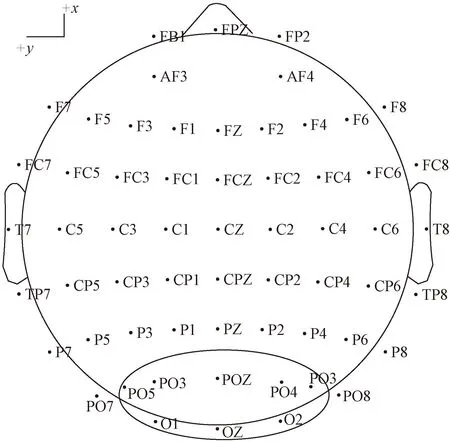
字母与数字为电极编号,如P2、PO4、F1等;椭圆圈出部分为采集导联分布图3 采集导联分布示意Fig.3 Distribution diagram of acquisition channels

为了去除肌电、眼电,还采集了M1、M2、VEOU、VEOL、HEOL、HEOR这6个特殊导联。脑电采集软件采用Curry7,在完成原始信号采集后,使用Curry7完成原始信号中的肌电、眼电的去除。

3 实验结果分析

3.1 比较方法介绍

为了验证所提方法,设置以下3种方法来处理同一数据集作为对比。

(1)功率谱密度分析的方法(PSD),直接提取出SSVEP信号中的功率谱密度特征,选取和刺激频率相匹配的几个特定的频段的功率信息,通过对不同频段的功率谱密度的大小进行比较,最后完成对实验信号的分类。

(2)典型相关性分析(CCA)的方法,直接对SSVEP信号进行典型相关性分析,计算出信号与参考信号间的相关系数,完成信号的分类。

(3)滤波器组典型相关性分析(FBCCA)的方法,先将SSVEP信号投入设置好的滤波器组中,提取出包含相关谐波特征的子带,再使用CCA来计算出子带信号与参考信号间的相关系数,最后求取所有子带和参考信号的相关性系数的加权平方和,完成信号的分类。

实验对比的参考标准主要为信号的分类准确率与信息传输率。

3.2 分类准确率分析

实验的计算在MATLAB R2020a环境中进行。8名受试者均进行了两次实验,共采集到640组实验信号。为了充分验证所提出的针对SSVEP信号识别算法的有效性,将采集到的实验信号通过0.5、1、1.5、2、2.5、3 s的时间窗,时间窗截取设置为有效实验信号2.5 s处,前后对称截取对应时间长度。对通过时间窗截取的实验信号分别通过PSD的方法、CCA、FBCCA和FBCCA与PSD分析结合的目标识别方法进行分类处理,统计受试者在不同时间窗长度的平均识别准确率,结果如图4所示。

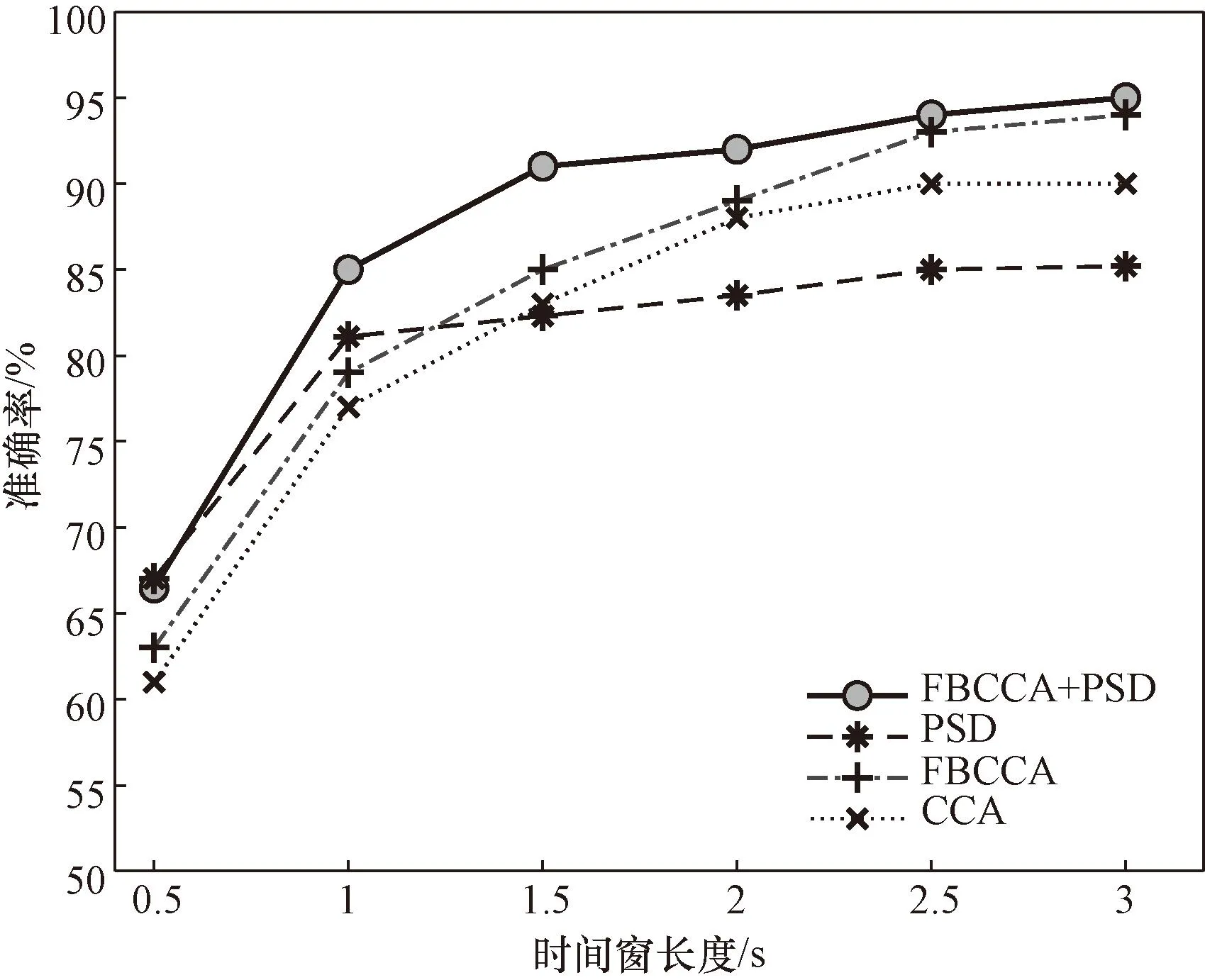
图4 不同时间窗长度识别准确率比较Fig.4 Comparison of recognition accuracy of different time window lengths

从图4可以看出,FBCCA与PSD分析结合的目标识别方法拥有最高的平均分类准确率。在时间窗较短时,0.5 s时,FBCCA与PSD分析结合的目标识别方法的准确率为66.47%,优于CCA的62.61%和FBCCA的63.98%。并且与PSD分析方法的67.02%准确率结果相近。在时间窗长度为1 s时,FBCCA与PSD分析结合的目标识别方法的准确率为86.61%,优于PSD分析方法的81.17%,CCA的76.23%和FBCCA的77.75%。而在时间窗较长时,3 s时,FBCCA与PSD分析结合的目标识别方法的准确率要大幅优于CCA和PSD分析的方法,且略优于FBCCA的方法,准确率达到94.78%。

在时间窗长度较短时,实验信号依然能够保存较完整的功率谱特征,如图5所示,对刺激频率为5 Hz,时间窗长度为0.5 s时OZ导联的信号进行功率谱分析,可以看到其功率谱密度特征仍十分明显。

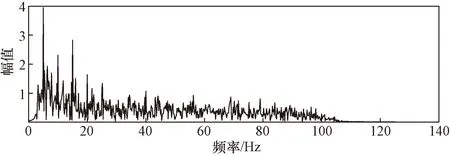
图5 刺激频率5 Hz,时间窗0.5 s的OZ导联功率谱密度Fig.5 Power spectral density of OZ channel with stimulation frequency of 5 Hz and time window of 0.5 s

因此FBCCA与PSD分析结合的目标识别方法能够保证在短时间窗情况下依然有较高的分类准确率。而在时间窗长度较长时,FBCCA拥有很高的识别准确率,保证了FBCCA与PSD分析结合的目标识别方法在长时间窗下的识别准确率。

将时间窗长度固定为3 s,统计不同刺激频段的实验信号在功率谱密度分析的方法、CCA、FBCCA和FBCCA与PSD分析结合的目标识别方法进行分类处理后的平均准确率,结果如图6所示。

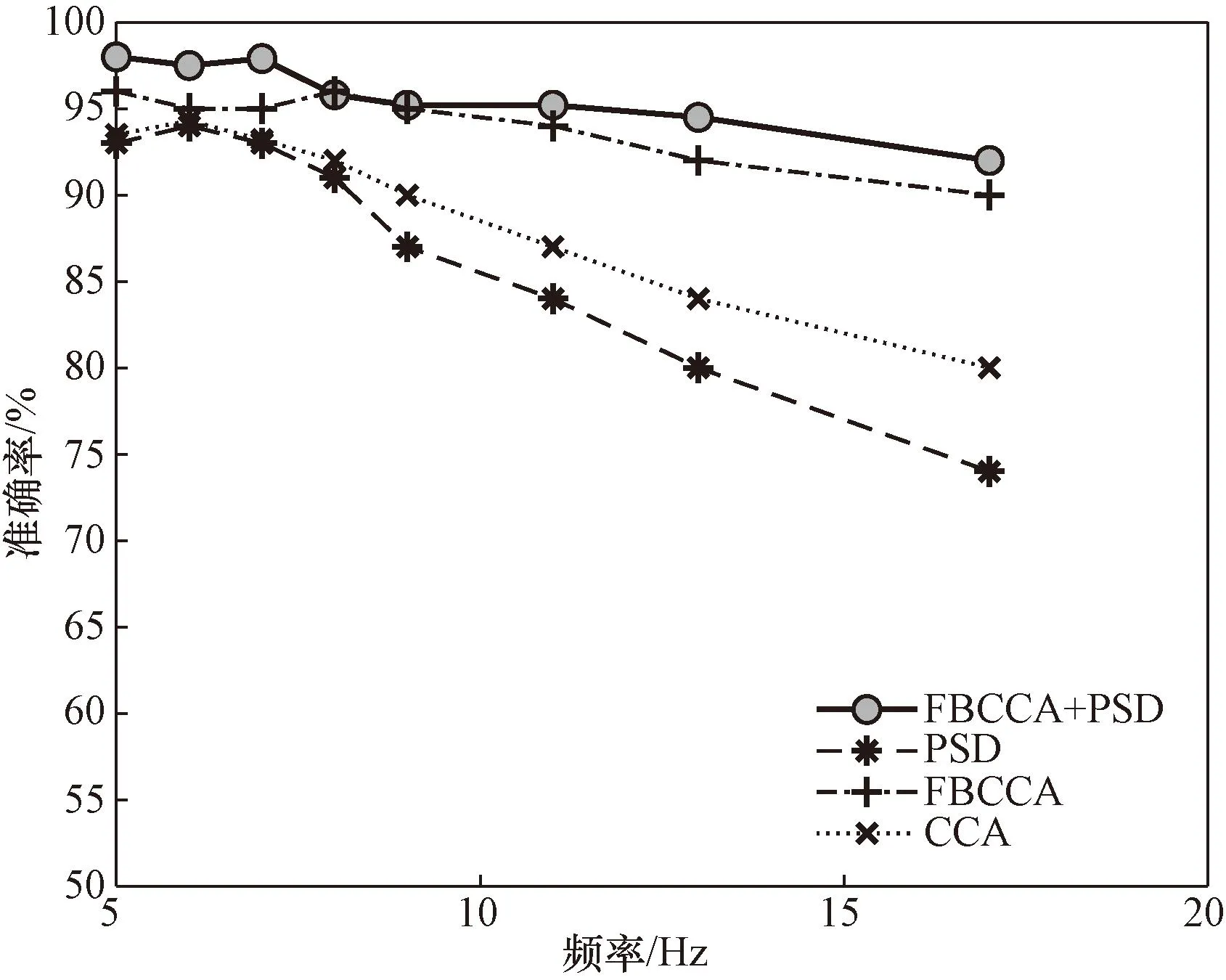
图6 3 s时间窗的识别准确率与刺激频率的关系Fig.6 Relationship between recognition accuracy of 3 s time window and stimulation frequency

从图6可以看出,在低频段部分,这4种算法都有较高的识别准确率,但随着刺激频率的升高,只有FBCCA与PSD分析结合的目标识别方法依然保持较高的识别准确率。这是因为随着刺激频率的升高,SSVEP的响应峰值会有所降低,只用PSD分析的方法不能很好的从信号中分辩出响应的频率特征。而FBCCA与PSD分析结合的目标识别方法通过FBCCA分析,能够将响应频率锁定在3个频段,再使用PSD分析,因此能够得到较好的分类结果。

3.3 信息传输率分析

计算这4种方法的信息传输率ITR[24], 计算公式为

(8)

式(8)中:T为时间窗长度;N为参与分类的刺激频率数;Pc为分类准确率。

由于每个被试的注意转移时间不同,因此计算ITR时使用的实际为SSVEP信号时长加0.5 s的注意转移时间。

经过计算,4种分类方法和时间窗长度对应的ITR如表2所示。

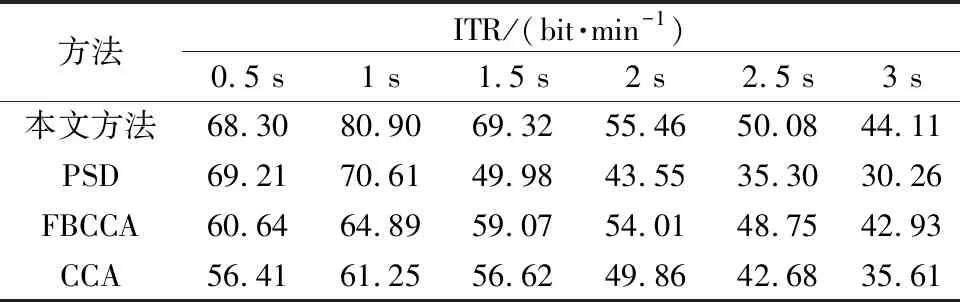
表2 不同时间窗长度对应的ITR比较Table 2 Comparison of ITR corresponding to different time window lengths

当SSVEP信号长度为1 s时,FBCCA与PSD结合的目标识别方法的ITR达到80.90 bit/min,比PSD、CCA和FBCCA均有较大提升。

4 结论

(1)针对传统的CCA和FBCCA进行SSVEP的特征提取与分类时,没有充分利用每个导联的单独功率谱密度特征信息;而使用PSD分析没有利用导联组整体特性的缺点,提出一种基于FBCCA与PSD分析的SSVEP识别算法,此算法利用FBCCA寻找到与目标SSVEP信号相似的参考信号,根据参考信号选择对应的滤波器组,让目标信号经过滤波器组,来降低噪声的影响,最后通过PSD分析来锁定最终的响应频率,完成SSVEP信号分类的方法。

(2)实验结果表明,本文算法在针对较短时间窗的SSVEP进行分类时,即可达到很好的分类效果。在时间窗口长度为0.5 s时,本文算法就能达到66.47%,优于PSD、CCA和FBCCA的分类准确率。针对刺激频率的变化,此算法可以在刺激频率为5～17 Hz保证较高的识别准确率与稳定性。同时此算法在时间窗口长度达到1 s时,信息传输率可以达到80.90 bit/min。表明所提出的一种基于FBCCA与PSD分析的SSVEP识别算法适用于SSVEP信号的分类,可以进一步提高分类的准确率,有较强的稳定性,能够达到较高的信息传输率。为SSVEP脑-机接口在分类准确率和稳定性提高等方面提供了实验借鉴。