非充气轮胎的滚动越障振动仿真分析

周海超，王荣乾，王国林，李慧云

（江苏大学 汽车与交通工程学院，江苏 镇江 212013）

作为车辆的重要组成部分，轮胎为车辆与路面接触的唯一部件，起到缓冲减振作用并提供车辆行驶所需的作用力，直接影响车辆的操纵稳定性、行驶安全性及乘坐舒适性等[1]。然而，传统的充气轮胎在滚动过程中容易被刺破而丧失机动性能，高速行驶时还易出现爆胎现象，存在严重的安全隐患，非充气轮胎则可以有效避免刺破、爆胎等危险，且兼具环保和轻量化等特点[2-3]。

虽然非充气轮胎具有优于充气轮胎的特点，但因振动问题依旧被限制在较高车速乘用车上应用。充气轮胎主要依靠其充气压力实现支撑、缓冲减振和提供作用力等作用，非充气轮胎则由轮辐结构实现这些功能[4-5]。相对于充气轮胎的质量分布均匀，非充气轮胎的支撑结构不连续致使其质量分布非均匀，从而引起刚度的非均匀，使轮胎在滚动过程中出现接地面积不连续、接地压力不均匀等现象，最终造成振动较大，影响车辆的平顺性和乘坐舒适性[6-8]。

非充气轮胎的振动问题一直都是轮胎研究的重点之一，K.K.MANGA[9]研究发现辐条振动是辐条在其胎面相应部位进入和离开接地区域时屈曲和回弹现象激发的共振。P.AMARNATH[10]采用正交矩阵研究幅条长度和曲率在内的9个几何参数对振动幅值的影响。B.SHASHANK[11]提出交替轮辐组的设计概念，通过将偶数辐条对设置为大曲率小厚度、奇数辐条对设置为小曲率大厚度来实现非充气轮胎的减振效果。N.AKSHAY[12]研究了轮辐和剪切带材料的改变对非充气轮胎振动的影响。这些非充气轮胎振动仿真分析的行驶均假设为平地行驶，并且所提取的作用力均为路面径向反作用力。

H.C.ZHOU等[13]开展了非充气轮胎的减振研究，对辐条式原始非充气轮胎（简称原始轮胎）和轮辐仿生优化非充气轮胎（简称优化轮胎）进行平地滚动仿真计算，通过分析路面径向反作用力的幅值来验证优化轮胎的减振效果。由于车辆在实际行驶中会遇到各种路面条件，即除有平坦路段外，还存在颠簸、坑洼等障碍物对车辆造成不同的冲击，因此，越障振动分析亦是轮胎振动研究的重点之一。C.W.MOUSSEAU等[14]针对充气轮胎提出了一种简单有效的二维轮胎新模型，准确预测了越过大障碍物时径向和纵向反作用力峰值随轮胎滚动速度的变化规律。C.F.WEI等[15]在充气轮胎越障分析中发现，随着障碍物高度的增大，轮胎的径向和纵向共振幅值均增大，且轮胎的滚动速度越大，径向共振幅值越大。Y.L.ZHANG等[16]通过试验验证了充气轮胎滚动越障分析得到的径向和纵向反作用力波动后，用整车模型进行了越障研究，结果表明，当越过凸出障碍物时，轮胎的变形随车辆的滚动速度和障碍物高度的增大而增大，但是越过凹坑障碍时其动态行为较复杂。在非充气轮胎的滚动越障动态研究中，S.CHAKRIT等[17]针对米其林集团的Tweel非充气轮胎（简称Tweel轮胎），采用有限元方法分析研究了其越过不同高度障碍物时在不同时刻的径向冲击力和变形行为。J.F.MA等[18]通过仿真分析发现，障碍物高度对非充气轮胎的变形和轮毂中心的加速度分布有较大影响，障碍物圆角半径对轮毂中心的加速度分布的影响较小，越障滚动速度对轮胎的变形影响较大，且滚动速度较低时其对轮胎的变形影响更大。

无论是平地滚动还是越障行驶，轮胎的振动对车辆的耐久性、操控性和乘坐舒适性等均有极大的影响。目前，非充气轮胎的平地滚动振动研究大多通过分析其路面径向反作用力的波动来研究其振动效果与影响因素；在越障动态分析中，无论是充气轮胎还是非充气轮胎均集中于分析轮毂的位移、作用力、速度、加速度波动，或是独立分析动态滚动下轮胎的应力、应变或轮胎与地面之间的动态接地力学行为。相较于充气轮胎，非充气轮胎与地面接触区域的径向和纵向反作用力同样受到路面条件、行驶状态或轮胎不均匀性的影响，从而引起波动，但是对于其振动力学特性却缺少全面、深入的研究。

本工作针对非充气轮胎严重的振动问题，对原始轮胎与优化轮胎进行滚动越障仿真分析，通过分析其越障时路面径向和纵向反作用力的时域波动与对应的频域幅值变化来研究不同滚动速度和不同障碍物高度对非充气轮胎振动的影响，并根据滚动越障时接地压力峰值的变化分析优化轮胎与原始轮胎的振动特性，从而为非充气轮胎的滚动越障振动提供更多的研究方法。

1 模型建立及验证

1.1 几何模型建立

本工作选用Tweel轮胎进行研究，其由轮毂、轮辐、带有加强层的柔性环和胎面4个部分组成。Tweel轮胎的几何模型尺寸参数采用B.SHASHANK研究所用的参数[11]，其几何结构和材料如图1所示：铝合金轮毂与轮辐连接并与轴装配；整个轮辐由25对聚氨酯材料的辐条对组成；聚氨酯柔性环由两层加强层分隔为3部分，由轮毂到胎面方向依次为内覆盖、剪切层和外覆盖；高强度钢材料的加强层提供轮胎所需的高刚度和强度；胎面与地面接触，为轮胎滚动提供所需的作用力。有限元网格划分时轮毂、轮辐、内外覆盖、剪切带和胎面采用C3D8R单元，加强层采用SFM3D4R单元。

图1 Tweel轮胎的几何结构和材料示意Fig.1 Diagram of geometry and materials of Tweel tire

1.2 有限元模型仿真与验证

利用Hypermesh软件对Tweel轮胎几何模型进行网格划分（轮辐网格数为2×24），然后导入Abaqus软件，利用Standard求解方法对模型进行3 665 N的径向静态加载的仿真分析并获取径向刚度曲线。其中，铝合金轮毂密度为2.8 Mg·m-3，模量为72 GPa，泊松比为0.33；聚氨酯密度为1.1 Mg·m-3，采用Marlow模型；高强度钢密度为7.8 Mg·m-3，模量为210 GPa，泊松比为0.29；胎面胶采用Neo-Hookean模型，密度为1.1 Mg·m-3，参数C10和D1分别为0.833和0.124。Tweel轮胎的网格划分与有限元模型如图2所示。

图2 Tweel轮胎的网格划分与有限元模型示意Fig.2 Diagram of mesh generation and finite element model of Tweel tire

Tweel轮胎的仿真与N.AKSHAY[12]研究中非充气轮胎的实测径向刚度曲线如图3所示。

图3 非充气轮胎的径向刚度曲线Fig.3 Radial stiffness curves of non-pneumatic tires

从图3可以看出，在整个加载过程中非充气轮胎的径向刚度仿真结果与实测结果较接近，且在3 665 N的径向负荷下两种轮胎的下沉量误差不足1%，验证了本工作建立的有限元模型可以准确反映非充气轮胎的力学特性，可以进行非充气轮胎的振动分析。

2 轮胎的滚动越障振动分析

固定路面，对轮辋中心施加径向负荷和滚动速度，运用Abaqus/Explicit模块进行平地滚动仿真计算，记录仿真时间，提取轮胎稳态滚动后时域内的径向激励力并将其转化为频谱图。

2.1 越障仿真分析

选取原始轮胎与优化轮胎进行滚动越障振动分析，原始轮胎为Tweel轮胎，优化轮胎取H.C.ZHOU等[13]研究的轮胎：首先将轮辐侧边缘进行非对称弧处理，实现类似于猫爪掌垫的摆动减振机理，验证非对称弧轮胎的减振效果后进行进一步优化而得到优化轮胎。该振动分析在平地和较高车速下进行。

借鉴以上研究成果，本工作针对原始轮胎与优化轮胎进行滚动越障振动分析，研究其在低速和越障时的减振效果和相关规律。本工作原始轮胎与优化轮胎的轮辐参数包含曲率（A）、厚度（B）和非对称弧长度（C），如图4和表1所示。图中，P点为辐条高度的上1/4点位置。

表1 原始轮胎与优化轮胎的轮辐参数Tab.1 Spoke parameters of original tire and optimized tire mm

图4 轮辐参数Fig.4 Spoke parameters

利用Abaqus/Explicit模块，约束非充气轮胎的径向自由度，通过路面向轮胎施加3 665 N的径向负荷，进行10，20和30 km·h-13种滚动速度下的越障仿真分析。采用库仑摩擦模型，胎面与路面之间的摩擦因数为0.7。非充气轮胎的滚动越障仿真模型如图5所示。

图5 非充气轮胎的滚动越障仿真模型Fig.5 Simulation model of rolling obstacle crossing of non-pneumatic tire

障碍物为矩形，保持其宽度不变，改变其高度形成3种障碍物（分别以O1，O2，O3代表），其具体尺寸如表2所示。为了使非充气轮胎由平地滚动至障碍物时能够实现较为平缓的过渡，从而避免障碍物尖端处出现接触不良甚至压溃的现象，将障碍物两顶点处进行圆弧处理，圆弧半径为障碍物高度的1/2。

表2 3种障碍物的尺寸Tab.2 Dimensions of 3 types of obstacles mm

2.2 障碍物高度和滚动速度对轮胎振动的影响

2.2.1 径向振动分析

提取原始轮胎与优化轮胎在不同滚动速度下越过障碍物时随时间变化的径向反作用力，分析两种轮胎分别在不同滚动速度和障碍物高度时的振动特性。原始轮胎与优化轮胎的时域内径向反作用力分别如图6和7所示，图中v为轮胎的滚动速度。

图6 原始轮胎越过3种障碍物的时域内径向反作用力Fig.6 Radial reaction forces in time domain of original tire crossing three types of obstacles

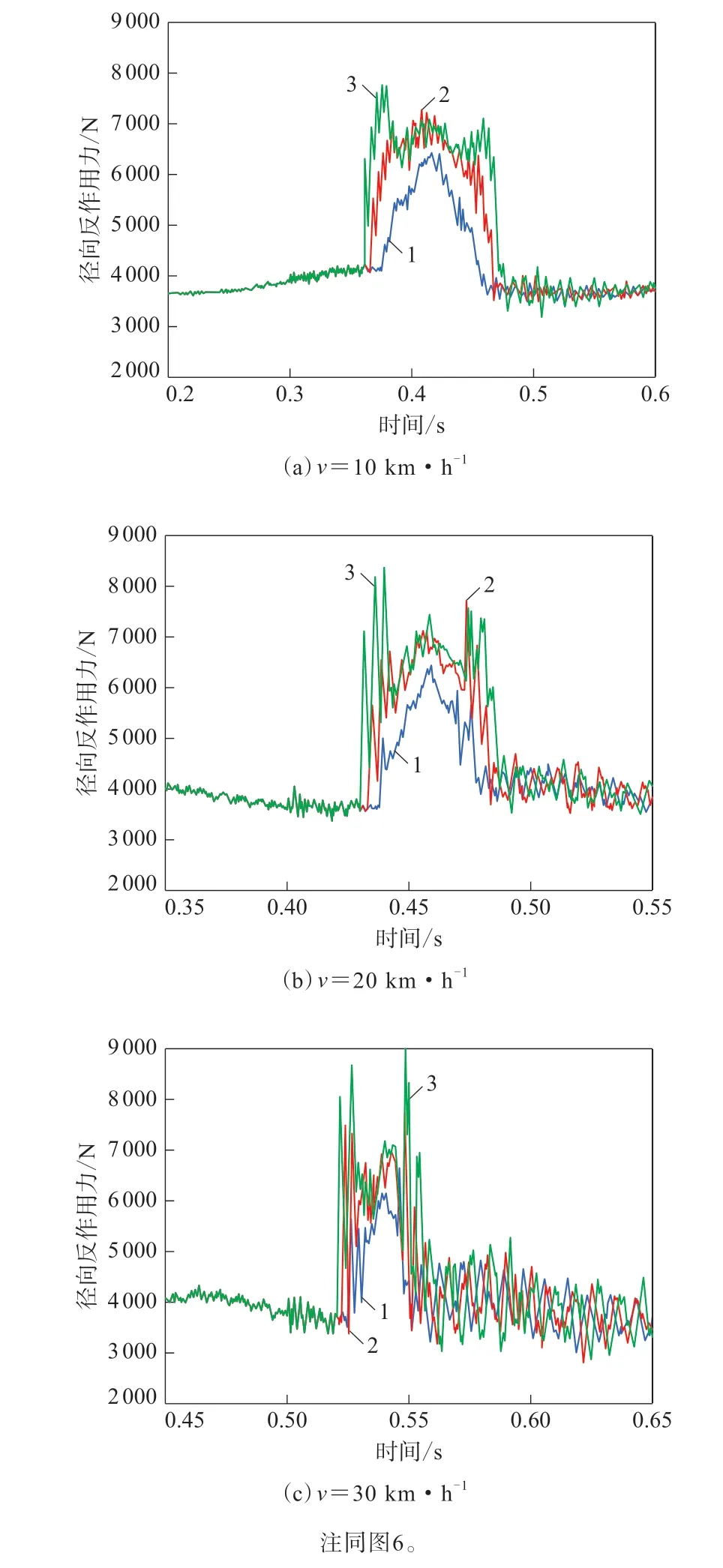
图7 优化轮胎越过3种障碍物的时域内径向反作用力Fig.7 Radial reaction forces in time domain of optimized tire crossing three types of obstacles

从图6和7可以看出：滚动越障时，随着障碍物高度的增大，原始轮胎与优化轮胎在不同滚动速度下的径向反作用力波动在局部和整体均呈增大趋势，即两种轮胎的振动随着障碍物高度的增大而愈加剧烈；与原始轮胎相比，优化轮胎滚动越障结束后的径向振动显著减小，即优化轮胎的越障减振作用主要体现在越障结束后，轮胎可以达到快速稳定的状态。这是由于轮胎在滚动越障仿真中的径向固定，当障碍物高度增大时，轮胎在径向将产生更大的变形，从而导致径向反作用力及其波动增大。为了更好地解释此规律，本工作将原始轮胎与优化轮胎滚动越障过程中的径向反作用力时域图转化为频谱图，通过比较其径向激励力幅值的大小研究障碍物高度对两种轮胎振动的影响，结果如图8和9所示。

图8 原始轮胎越过3种障碍物的频谱Fig.8 Spectrums of original tire crossing three types of obstacles

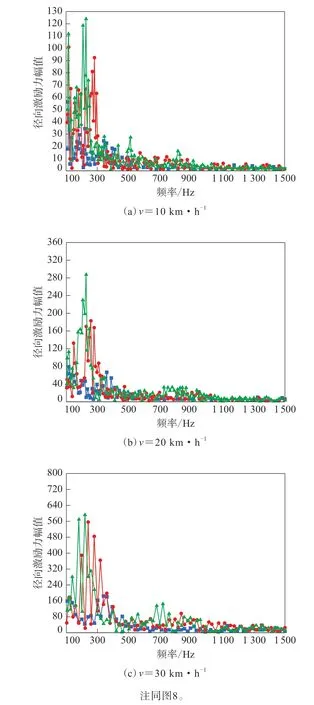
图9 优化轮胎越过3种障碍物的频谱Fig.9 Spectrums of optimized tire crossing three types of obstacles

从图8和9可以看出，滚动越障时，随着障碍物高度的增大，原始轮胎与优化轮胎在不同滚动速度下的径向激励力幅值明显增大，即轮胎的振动增强。

原始轮胎与优化轮胎的径向振动PA1值和RMS值（分别为频谱图中对应径向激励力幅值的最高峰值及其偏差）分别如表3和4所示。结合表3和4中的具体量化幅值可以进一步验证图8和9中规律的可靠性。

表3 原始轮胎的径向振动PA1值和RMS值Tab.3 PA1 values and RMS values of radial vibration of original tire

表4 优化轮胎的径向振动PA1值和RMS值Tab.4 PA1 values and RMS values of radial vibration of optimized tire

将表3和4中的数据进行整理，得到原始轮胎与优化轮胎的径向振动PA1值和RMS值随轮胎滚动速度及障碍物高度增减的变化情况。原始轮胎与优化轮胎的径向激励力幅值与滚动速度和障碍物高度的关系如图10所示。

图10 原始轮胎和优化轮胎的径向振动幅值与滚动速度和障碍物高度关系Fig.10 Relationship between radial vibration amplitudes of original tire and optimized tire and rolling speeds and obstacle heights

从图10可以看出：在障碍物高度相同时，随着滚动速度的增大，两种轮胎撞击并越过障碍物的时间会缩短，轮胎受到的冲击会更大，PA1值和RMS值也相应呈现逐渐增大的现象；在两种轮胎滚动速度相同时，随着障碍物高度的增大，轮胎径向激励力幅值也相应增大，即滚动速度和障碍物高度的增大均会加剧轮胎的振动。

2.2.2 纵向振动分析

纵向反作用力的提取方法与径向反作用力相同，即提取两种轮胎在不同滚动速度下越过障碍物时纵向反作用力随时间变化的数据，分析滚动速度和障碍物高度对轮胎振动的影响。由于纵向反作用力的分析过程和径向反作用力类似，在此只展示轮胎在滚动速度为20 km·h-1时越过障碍物的时域内纵向反作用力及其频谱，分别如图11和12所示。

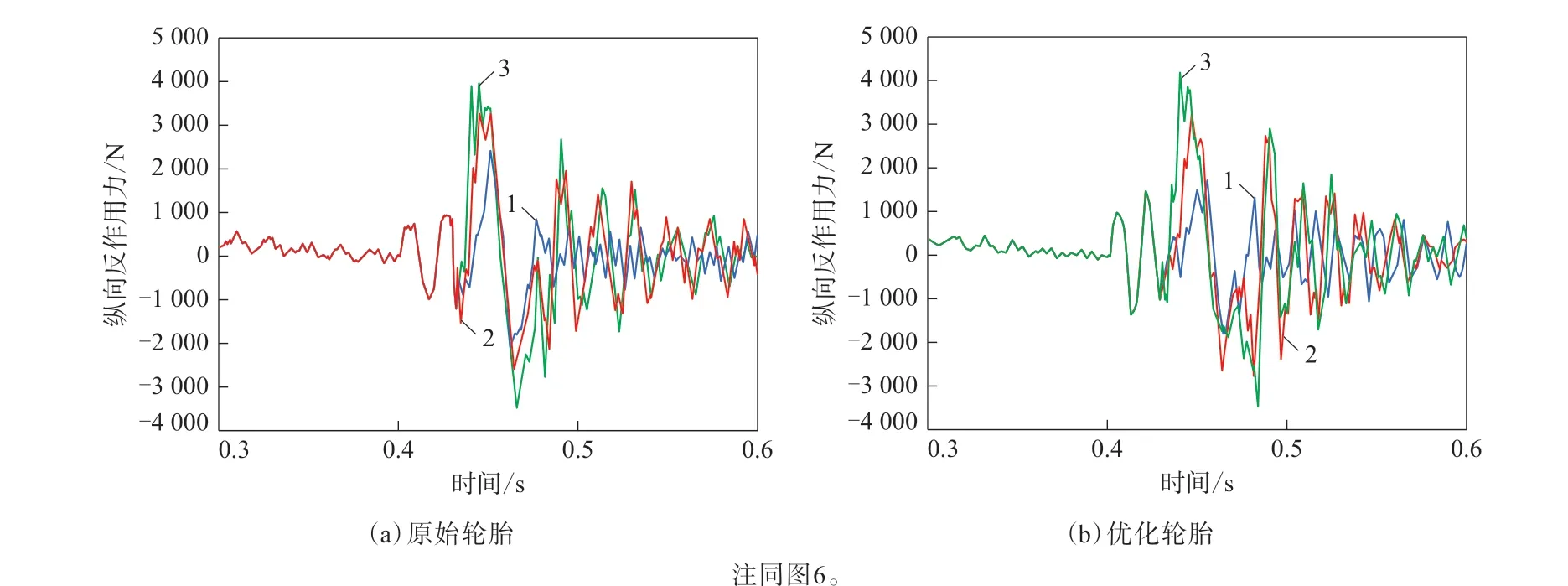
图11 轮胎以20 km·h-1滚动速度越过3种障碍物的时域内纵向反作用力Fig.11 Longitudinal reaction forces in time domain of tires crossing three types of obstacles at speed of 20 km·h-1

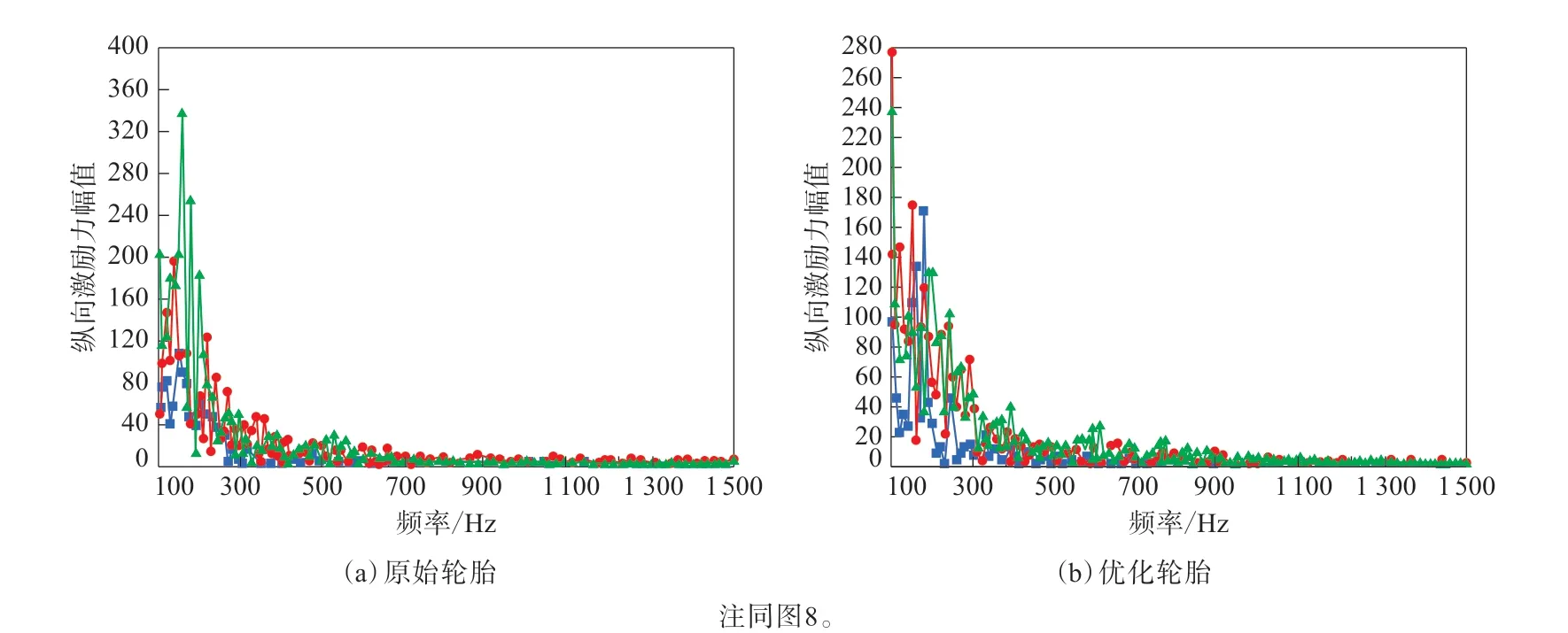
图12 轮胎以20 km·h-1滚动速度越过3种障碍物的频谱Fig.12 Spectrums of tires crossing three types of obstacles at speed of 20 km·h-1

从图11和12可以看出：由于两种轮胎从接触障碍物到完全处于障碍物上的过程相当于轮胎滚动速度减小的制动过程，而越过障碍物并触地的过程类似于轮胎加速的驱动状态，轮胎越障时纵向反作用力呈现出先沿轮胎行驶方向突然增大再逐渐减小至零，继而沿与行驶方向的反方向增大的现象；随着障碍物高度的增大，原始轮胎与优化轮胎的纵向反作用力波动明显增大，对应其激励力幅值亦显著增大，即振动增强。这是由于随着障碍物高度的增大，轮胎越过障碍物需要更大的驱动力来克服阻力，从而导致纵向反作用力及其波动增大。为了详细研究原始轮胎与优化轮胎的纵向振动强度与滚动速度和障碍物高度的关系，将两种轮胎在不同滚动速度和障碍物高度下的纵向振动PA1值和RMS值进行汇总，结果如表5和6所示。

表5 原始轮胎的纵向振动PA1值和RMS值Tab.5 PA1 values and RMS values of longitudinal vibration of original tire

表6 优化轮胎的纵向振动PA1值和RMS值Tab.6 PA1 values and RMS values of longitudinal vibration of optimized tire

将表5和6中原始轮胎与优化轮胎的纵向振动PA1值和RMS值转化成图，结果如图13所示。

图13 原始轮胎与优化轮胎的纵向振动幅值与滚动速度大小和障碍物高度的关系Fig.13 Relationship between longitudinal vibration amplitudes of original tire and optimized tire and rolling speeds and obstacle heights

结合表5，6和图13可以看出：无论原始轮胎还是优化轮胎，在障碍物高度相同时，随着轮胎的滚动速度增大，其纵向振动PA1值和RMS值增大；在轮胎滚动速度相同时，随着障碍物高度的增大，轮胎纵向振动的PA1值和RMS值增大，即两种轮胎的纵向激励力幅值与滚动速度和障碍物高度成正比。

在原始轮胎与优化轮胎的径向和纵向振动与滚动速度和障碍物高度的研究中可以得出，车辆在低速越障时，随着车速和障碍物高度的增大，轮胎的径向和纵向振动强度都呈现出相同的变化规律，即出现较明显的增大趋势。

2.3 原始轮胎与优化轮胎的振动对比分析

2.3.1 径向振动对比

为研究原始轮胎与优化轮胎的越障振动特性，将两种轮胎在不同滚动速度和障碍物高度下的径向振动PA1值和RMS值进行对比，结果如图14所示。

图14 原始轮胎与优化轮胎的径向振动幅值对比Fig.14 Comparison of radial vibration amplitudes of original tires and optimized tires

从图14可以看出：在滚动速度为10 km·h-1时，原始轮胎与优化轮胎的径向振动PA1值和RMS值曲线几乎重合，径向振动幅值变化不明显；当滚动速度大于20 km·h-1后，原始轮胎与优化轮胎的径向振动幅值差距开始显现，并且优化轮胎的径向振动幅值曲线的斜率减小，体现出随着障碍物高度的增大，优化轮胎较原始轮胎呈现较好的减振缓冲效果，且最终在障碍物高度为30 mm时，PA1值和RMS值较原始轮胎分别减小了13.85%和13.53%；在滚动速度为30 km·h-1、障碍物高度为10和30 mm时优化轮胎的径向振动幅值较原始轮胎减小较为明显，虽然在障碍物高度为20 mm时优化轮胎的振动幅值增大较快并超过原始轮胎，但是在高低障碍物下的幅值差原始轮胎为472.76，优化轮胎为412.65，即从整体来看，优化轮胎在此速度下的径向振动幅值随障碍物高度的变化依旧比原始轮胎小，且在障碍物高度为30 mm时，优化轮胎较原始轮胎的PA1值和RMS值分别降低了17.75%和6.7%。因此，优化轮胎虽然在有些滚动速度和障碍物高度下的径向振动幅值较原始轮胎有所上升，但从整体来看，优化轮胎在低速越障过程中依旧表现出良好的减振缓冲效果。

2.3.2 纵向振动对比

将原始轮胎与优化轮胎在不同滚动速度和障碍物高度下的纵向振动PA1值和RMS值进行对比，结果如图15所示。

图15 原始轮胎与优化轮胎的纵向振动幅值对比Fig.15 Comparison of longitudinal vibration amplitudes of original tires and optimized tires

从图15可以看出：在滚动速度为10 km·h-1时，不同于原始轮胎与优化轮胎的径向振动幅值差较小，纵向振动的PA1值和RMS值已出现明显的差距，并且优化轮胎的纵向振动幅值大于原始轮胎；在滚动速度为20 km·h-1时，虽然障碍物高度为10 mm时优化轮胎的纵向振动幅值大于原始轮胎，但是优化轮胎在此速度下的减振效果是在障碍物高度的变化中体现的，优化轮胎的纵向振动幅值曲线的斜率较原始轮胎有大幅减小，使得轮胎在障碍物高度增大时不会出现剧烈的振动变化，且最终在障碍物高度为30 mm时优化轮胎的纵向振动PA1值和RMS值较原始轮胎分别减小了29.72%和28.69%；在滚动速度为30 km·h-1时，随着障碍物高度的增大，优化轮胎的纵向振动幅值小于原始轮胎，表现出其在较高车速下优异的减振效果。在原始轮胎与优化轮胎的纵向振动分析中发现，优化轮胎在较低车速下几乎不具有纵向减振效果，且与障碍物高度是否变化无关；随着滚动速度的增大，优化轮胎的减振效果显现，且其纵向振动幅值曲线整体较为平缓，其在越障时可以更好地适应滚动速度和障碍物高度的变化，越障比较稳定。

2.3.3 动态接地压力分析

由于非充气轮胎的刚度的非均匀性，其在滚动过程中出现接地面积不连续和接地压力不均匀等现象，由此引发较为严重的振动问题。因此，针对优化轮胎的减振效果，分析其在滚动过程中的接地力学特性极为重要。在原始轮胎与优化轮胎的径向振动分析中，滚动速度为10 km·h-1时两种轮胎的径向振动幅值变化不明显，而在滚动速度为30 km·h-1时优化轮胎在障碍物高度为20 mm出现较大的径向振动幅值增大现象（参考性有待进一步探究）；在原始轮胎与优化轮胎的纵向振动分析中，在滚动速度为20 km·h-1时才开始体现出减振效果，且比滚动速度为30 km·h-1时的优化效果更明显。因此，选择滚动速度为20 km·h-1作为接地力学分析速度，研究不同障碍物高度下两种轮胎接地力学特性的变化。同样为了分析不同滚动速度下优化轮胎与原始轮胎的接地情况，选择30 mm的障碍物高度进行研究。

本工作确定的越障过程为轮胎越障开始、接触障碍物、完全在障碍物上、即将脱离障碍物和越障结束5个步骤，如图16所示。

图16 轮胎越障过程Fig.16 Tire obstacle crossing processes

本工作选择接地压力峰值作为分析对象，通过5个步骤接地压力峰值标准差来分析原始轮胎与优化轮胎的接地压力峰值波动情况，研究接地压力峰值标准差与减振的相关性。

原始轮胎与优化轮胎在滚动速度为20 km·h-1和不同障碍物高度下5个越障步骤的接地压力峰值如表7所示，在障碍物高度为30 mm和不同滚动速度下5个越障步骤的接地压力峰值如表8所示。

表7 原始轮胎与优化轮胎在滚动速度为20 km·h-1和不同障碍物高度下5个越障步骤的接地压力峰值Tab.7 Ground pressure peaks of original tire and optimized tire in five obstacle crossing steps at rolling speed of 20 km·h-1 and different obstacle heights MPa

表8 原始轮胎与优化轮胎在障碍物高度为30 mm和不同滚动速度下5个越障步骤的接地压力峰值Tab.8 Ground pressure peaks of original tire and optimized tire in five obstacle crossing steps at obstacle height of 30 mm and different rolling speeds MPa

5个越障步骤中原始轮胎与优化轮胎的接地压力峰值标准差如图17所示。

图17 5个越障步骤中原始轮胎与优化轮胎的接地压力峰值标准差Fig.17 Standard deviations of ground pressuree peaks of original tires and optimized tires in five obstacle crossing steps

从图17（a）可以看出：在障碍物高度为10 mm时，优化轮胎的接地压力峰值标准差大于原始轮胎，体现了优化轮胎在越障的5个步骤中接地压力峰值有较大波动，对应优化轮胎的径向和纵向振动幅值增大，振动增强；在障碍物高度为20和30 mm时，优化轮胎的接地压力峰值标准差均小于原始轮胎，说明优化轮胎在越障滚动过程中的接地压力波动较小，体现出接地压力变化的稳定性，对应优化轮胎的径向和纵向振动幅值减小，优化轮胎起到优异的减振效果。

从图17（b）可以看出：滚动速度为10 km·h-1时，优化轮胎的接地压力峰值标准差大于原始轮胎；滚动速度为20和30 km·h-1时，优化轮胎的接地压力峰值标准差小于原始轮胎，相较于原始轮胎，优化轮胎的径向和纵向减振效果显著。

总之，无论是在滚动速度不变而障碍物高度改变，还是在障碍物高度不变而滚动速度改变时，原始轮胎与优化轮胎的接地压力峰值标准差偏大均造成轮胎在越障时接地压力波动变大，造成振动幅值和振动强度增大，即原始轮胎与优化轮胎的接地压力峰值标准差与其径向和纵向振动有一定关联性，接地压力峰值标准差能够在一定程度上表征轮胎的振动幅度及减振效果。

3 结论

本工作建立了非充气轮胎模型，对比分析了优化轮胎和原始轮胎的越障振动，研究了不同滚动速度和障碍物高度对两种轮胎径向和纵向振动的影响以及优化轮胎的减振效果，分析了轮胎越障过程的接地压力峰值标准差，得到如下结论。

（1）无论是原始轮胎还是优化轮胎，在滚动速度和障碍物高度增大时，其径向和纵向振动幅值均会增大，即振动增强。

（2）与原始轮胎相比，优化轮胎在滚动速度和障碍物高度变化时振动幅值体现出较为平缓的变化，其在滚动速度和障碍物高度变化时能够保持较好的稳定性，不会因越障条件改变产生剧烈的振动变化。

（3）与原始轮胎相比，优化轮胎的接地压力峰值标准差变化与其径向和纵向振动强度一致，接地压力峰值标准差可以作为判断非充气轮胎振动强度的参数之一。