丙烯腈含量对氢化丁腈橡胶热学性能影响的分子动力学模拟研究
苏明龙,王泽鹏,姚秀龙,杨 剑,马连湘,苗展丽
(青岛科技大学 机电工程学院,山东 青岛 266061)
氢化丁腈橡胶(HNBR)是将丁腈橡胶(NBR)分子主链上的丁二烯单元进行选择性加氢而制得的一种高饱和度特种橡胶材料[1-2],其制备过程见图1。因具有优异的物理性能以及耐热性能、耐油性能和耐化学腐蚀性能等[3-4],HNBR在汽车、航空航天、石油等领域应用十分广泛[5]。
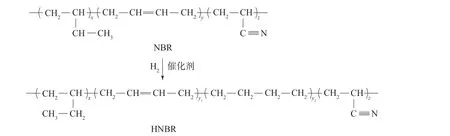
图1 HNBR的制备过程Fig.1 Preperation process of HNBR
丙烯腈(ACN)含量是影响HNBR性能的关键结构参数。张成龙等[6-7]研究了ACN质量分数对HNBR胶料力学性能和耐疲劳性能的影响,结果表明随着ACN质量分数的增大,HNBR胶料的交联密度增大,100%定伸应力、拉伸强度和撕裂强度提高,ACN质量分数对HNBR胶料的耐疲劳性能也有显著影响。
近年来,分子动力学(MD)模拟技术广泛地应用于聚合物热学、电学和力学性能等的研究[8]。N.MOLINARI等[9]利用MD模拟技术,通过饱和NBR分子主链—C=C—建立了交联度可调的HNBR分子模型,将模拟所得的HNBR的密度和玻璃化温度(Tg)与试验结果对比,验证了模拟的准确性。B.G.XIE等[10]通过MD模拟技术与试验相结合的方法,准确分析了交联和填充对聚异戊二烯橡胶胶料力学性能和热性能的影响。以上研究表明,MD模拟技术可以准确模拟聚合物材料的密度、力学性能、耐低温性能和热性能等,并且可以获取材料在微观层面的特殊属性,探究聚合物材料的微观与宏观性质的关联性。
本工作基于HNBR的合成过程,利用美国Accelrys公司开发的Materials Studio 2019软件构建HNBR分子模型,分析ACN质量分数对HNBR热导率(λ)和Tg的影响,通过分析HNBR在玻璃化转变过程中不同势能的变化情况,揭示其发生玻璃化转变的微观机理。
1 实验
1.1 模型构建及优化
NBR是由ACN和丁二烯聚合而成的,丁二烯有顺式、反式和乙烯基丁二烯3种同分异构体,其中以反式丁二烯为主[9]。基于NBR制备HNBR的实际过程,本研究在模型构建过程中未考虑丁二烯的异构,即认为x为0,又因为HNBR的饱和度通常接近100%,即HNBR分子主链不含有不饱和双键,因此y1也为0。由于NBR中ACN质量分数通常在18%~50%之间[11],因此本工作按照表1(NA和NB分别为HNBR分子链中ACN和丁烷链段数量)中ACN和丁烷链段数量的比例,利用Materials Studio 2019软件中的Build Random Polymer功能构建聚合度为50、不同ACN质量分数的HNBR分子链(a~e);利用Amorphous Cell模块构建周期性重复单元盒子(f~j),其中每一个盒子包含8条分子链,预设盒子密度为0.95 kg·cm-3,模型构建过程如图2所示。
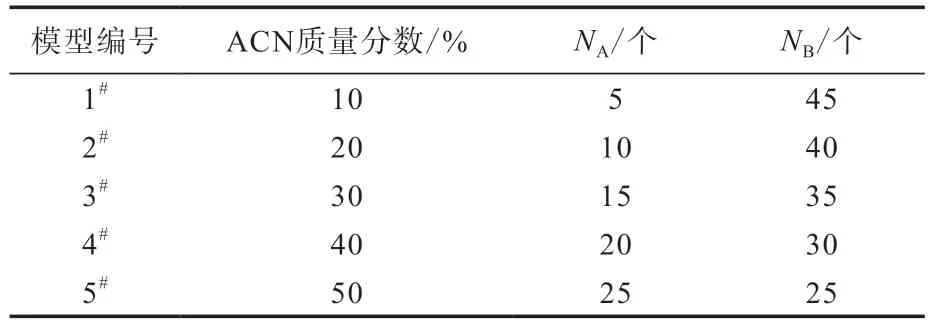
表1 HNBR分子链的结构参数Tab.1 Structure parameters of HNBR molecular chain
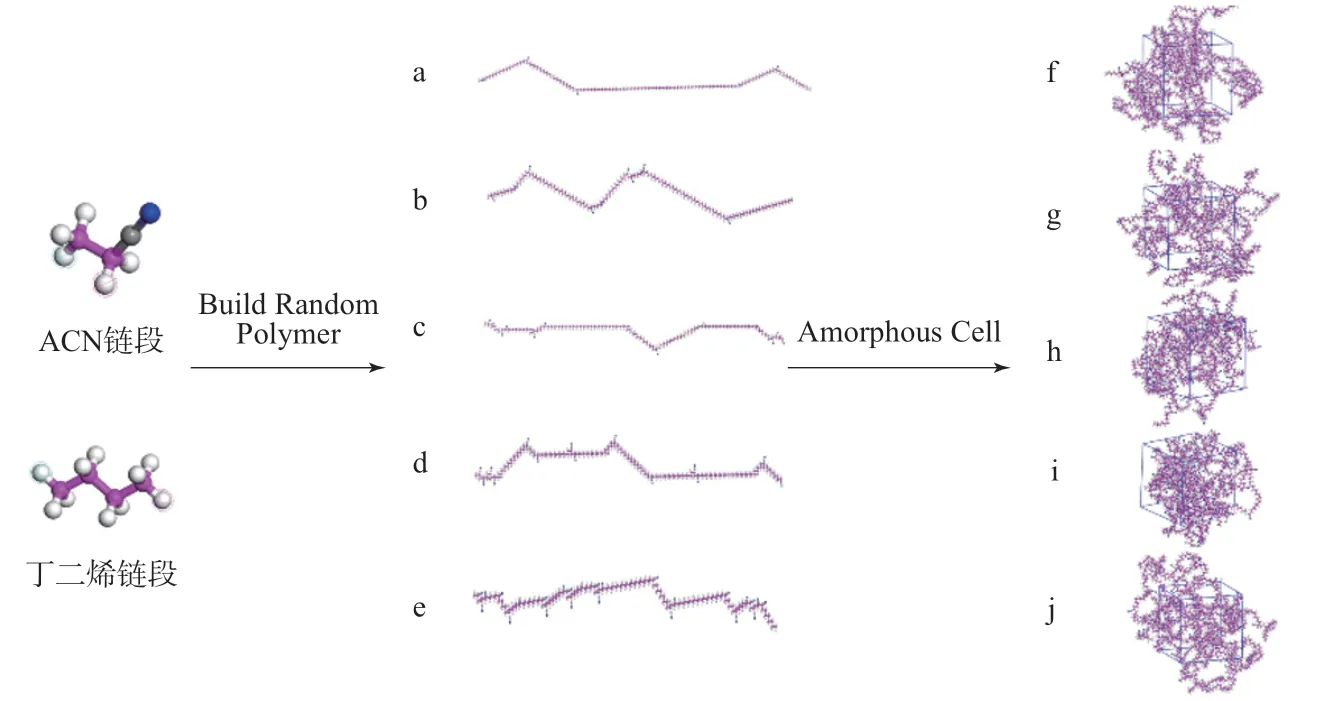
图2 模型的构建过程Fig.2 Construction process of model
为使模型达到合理的结构,需对模型进行充分地弛豫,弛豫过程如下。(1)结构优化;(2)退火:从200 K到400 K进行5个循环的能量退火,每个温度点在NVT系综下进行50 ps的动力学平衡;(3)在NVT系综下进行动力学平衡,温度为298 K,模拟时间长度为500 ps;(4)在NPT系综下进行动力学平衡,温度为298 K,压力为0.1 MPa,弛豫时间为1 ns,时间步长为1 fs,截断半径为15.5 Å。所有运算均在Materials Studio 2019软件上完成,MD计算均采用周期性边界条件,选取COMPASSⅡ力场,分别使用Andersen和Berendsen方法进行温度和压力控制。
1.2 测试方法
1.2.1λ
利用非平衡分子动力学(NEMD)方法[12]模拟计算HNBR的λ。NEMD通过高温区速度较小的粒子与低温区速度较大的粒子交换,使高温区的温度达到最高,低温区的温度达到最低,进而在体系内形成由高温区到低温区的恒定热流。基于傅里叶定律,可以计算出模型的λ。傅里叶定律如式(1)所示。
式中JX为热流量,∂T/∂X为温度梯度。
将模型沿Z方向划分为40个小格,中间为低温区,两端为高温区,当模型达到稳态后,JX可由式(2)计算。
式中,Δε为改变热板或冷板的能量而产生的温度差,S为垂直于热流方向的横截面积,Δt为施加JX的时间间隔。
1.2.2Tg
首先将平衡后的模型温度升高至330 K,在NPT系综下平衡500 ps,然后以20 K为步长降低温度,每次降温后在NPT系综下平衡200 ps。选取每个温度平衡的最后50 ps,共计100 帧结构,统计其比体积的平均值,并对其进行双线性拟合,比体积-温度的曲线斜率发生变化时对应的温度即为Tg。
2 结果与讨论
2.1 λ
1#—5#模型的λ分别为0.23,0.20,0.18,0.15和0.14 W·m-1·K-1,可见随着ACN质量分数的增大,HNBR的λ逐渐减小,与ACN质量分数为10%的HNBR相比,ACN质量分数为20%,30%,40%和50%的HNBR的λ分别减小了13.0%,21.7%,34.8%和39.1%。
用径向分布函数[13](RDF)分析ACN质量分数影响HNBR的λ的原因。RDF表征在距离原子一定距离的地方找到另一个原子的概率,可以反映模型的有序性。RDF的计算公式如下:
式中:g(r)越大表示与中心原子距离为r处的相邻原子越多,聚合物的有序性更高;Nα和Nβ为原子α和β的数目;V是模型的体积;nαβ(r)是在(r-Δr/2,r+Δr/2)范围内原子α和β的数目。
HNBR的RDF图像如图3所示,5种HNBR的RDF曲线整图重合[图3(a)]。
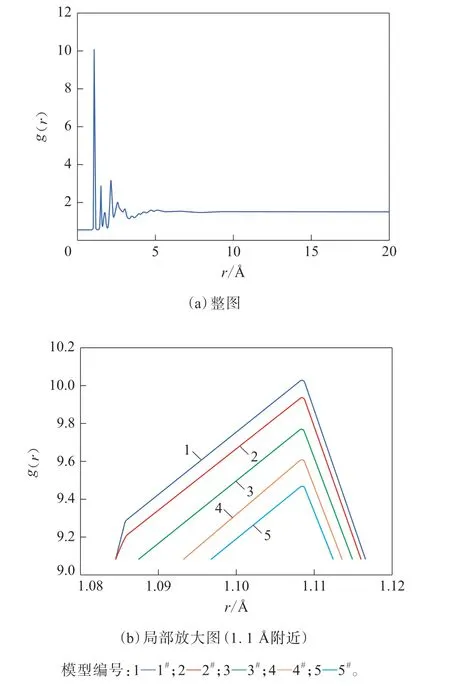
图3 HNBR的RDF图像Fig.3 RDF images of HNBR
从图3可以看出,5种HNBR的RDF曲线主峰在1.11 Å附近,且随着ACN质量分数的增大,RDF曲线峰值逐渐从10.04减小到9.47。这表明HNBR的有序性随ACN质量分数的增大逐渐下降,这与X.Zhang等[14]的研究成果是一致的。分析认为,聚合物的导热主要依靠无规排列的分子围绕一个固定位置的热振动将能量依次传递给相邻分子[15],ACN质量分数增大使得HNBR的有序性降低,无序结构导致声子扩散传递时的平均自由程降低,声子散射严重,HNBR的热阻增大,λ减小。
2.2 Tg
Tg是指物质由玻璃态转变为高弹态所对应的温度。HNBR的比体积-温度曲线如图4所示,Tg的模拟值与试验值对比如图5所示。
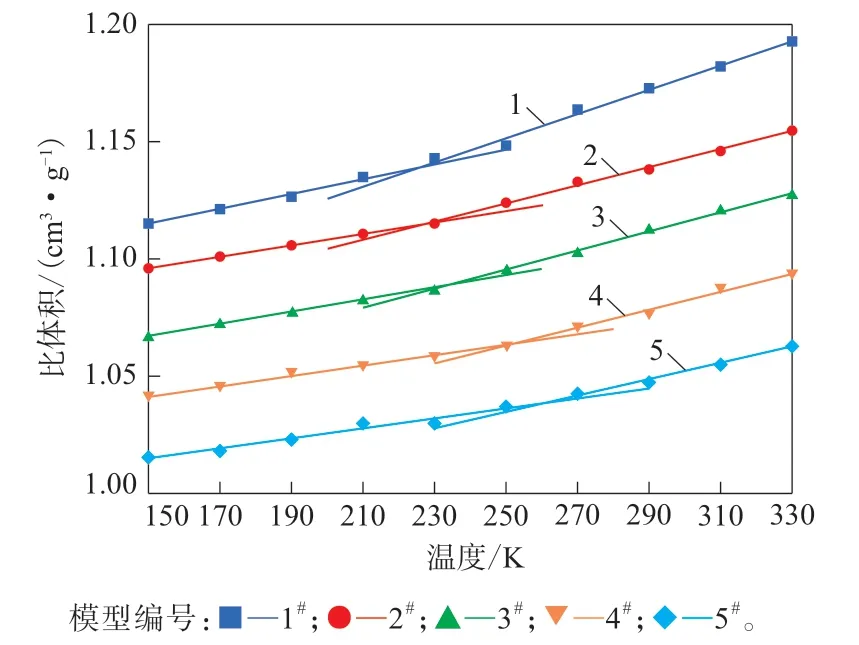
图4 HNBR的比体积-温度曲线Fig.4 Specific volume-temperature curves of HNBR
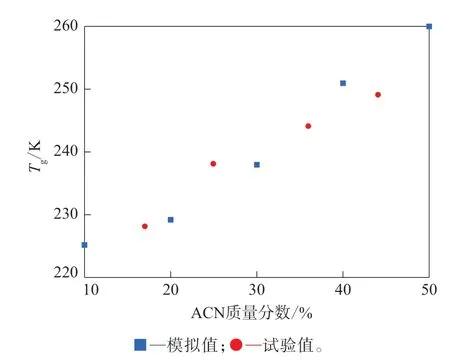
图5 HNBR的Tg模拟值与试验值对比Fig.5 Comparison between simulated and experimental values of Tg of HNBR
从图4可以看出:ACN质量分数不同的HNBR的比体积-温度的曲线斜率存在明显的不连续性,HNBR在曲线斜率突变点(拐点)发生了从玻璃态到橡胶态的二级相变;1#—5#模型的Tg依次为225.25,229.28,238.09,251.02和260.33 K。
从图5可以看出,本次模拟准确预测了HNBR的Tg随ACN质量分数的增大而增大的趋势。这是因为随着ACN质量分数的增大,HNBR的分子主链孤立双键减小,分子柔顺性下降;另一方面HNBR分子链侧基的极性增强,链间相互作用力大,侧基内旋转困难,这也会致使分子柔顺性下降,从而导致HNBR的Tg升高,耐低温性能下降。
HNBR分子的键角弯曲能、键能、非键能和二面角扭转能在Tg附近随温度的变化情况如图6—9所示。
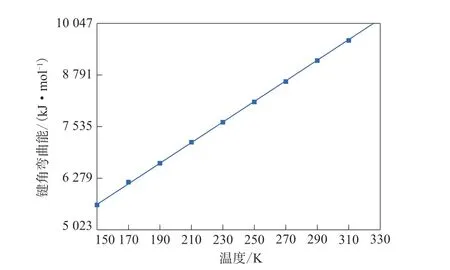
图6 HNBR分子的键角弯曲能Fig.6 Bond angle bending energies of HNBR molecule
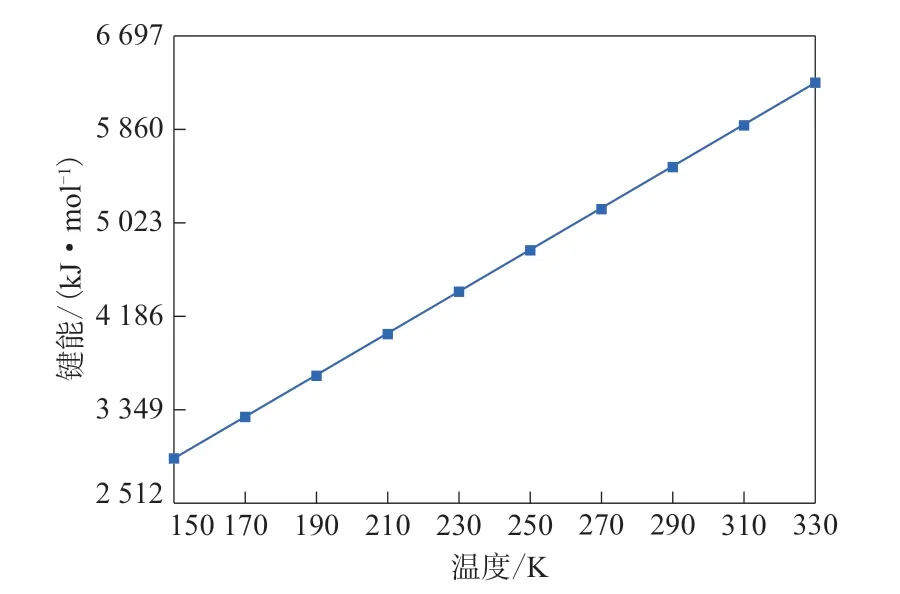
图7 HNBR分子的键能Fig.7 Bond energies of HNBR molecule
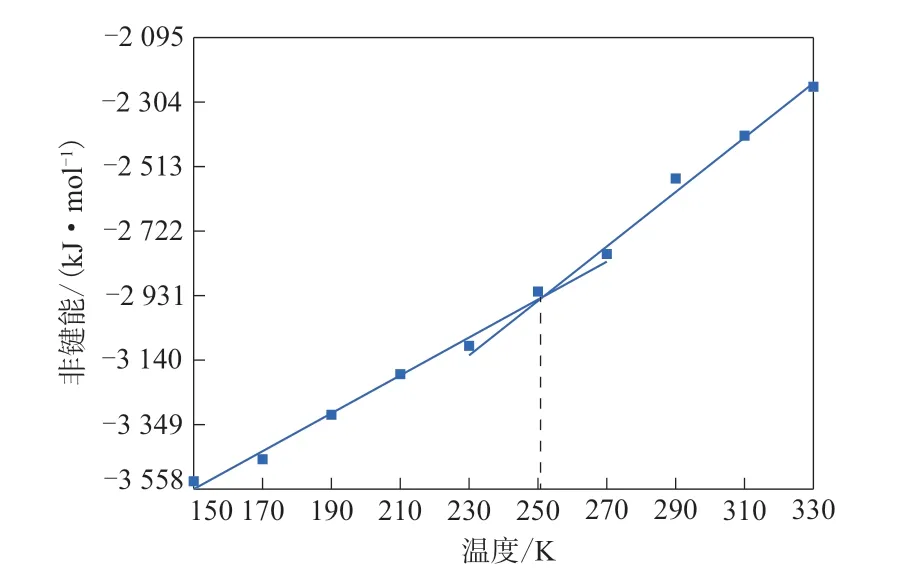
图8 HNBR分子的非键能Fig.8 Non bond energies of HNBR molecule
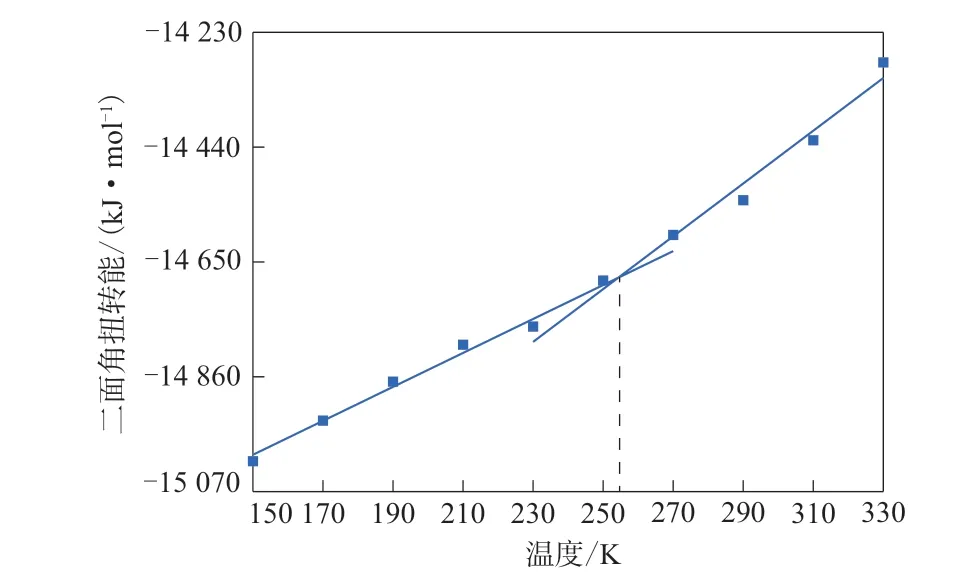
图9 HNBR分子的二面角扭转能Fig.9 Dihedral angle torsional energies of HNBR molecule
从图6—9可以看出,温度由150 K升高到330 K的过程中,HNBR分子的键角弯曲能和键能呈现均匀增长趋势,而非键能和二面角扭转能的曲线斜率随温度的升高发生突变,拐点出现在250 K附近,非常接近预测的HNBR的Tg。据此可以得出,分子的键角弯曲能和键能的自由度在HNBR发生玻璃化转变时处于平衡状态,而非键能和二面角扭转能在HNBR的玻璃化转变过程中起着至关重要的作用,温度低于Tg时,构象波动的速率不足以平衡非键能和二面角扭转能的自由度,温度高于Tg时,热波动足以平衡二者的自由度。
3 结论
(1)随着ACN质量分数的增大,HNBR分子链的取向性下降,无序结构导致声子扩散传递时的平均自由程降低,声子散射严重,HNBR的λ减小。
(2)通过比体积-温度关系模拟得到的HNBR的Tg与试验值吻合良好。随着ACN质量分数的增大,HNBR分子链中孤立双键减少,且分子链的极性增强,链间相互作用力大,侧基内旋转困难,分子柔顺性降低,HNBR的Tg升高,耐低温性能下降。
(3)在HNBR发生玻璃化转变的过程中,其分子的键角弯曲能和键能的自由度较为平稳,非键能和二面角扭转能发挥重要的作用。

