基于UKF-WNN 混合模型的海管段塞流预测与控制方法研究

周 波，廉晓龙，李 斌，孙 楠，黄 磊，王 昆

（1.合肥通用机械研究院有限公司，合肥 2300311；2.中海油田服务股份有限公司，天津 300456）

0 引言

在海洋油气开发过程中，通常采用海管将油井产出的油气混合流体输送至海上平台上进行处理。在这个过程中，启停操作、清管作业等可能会使海管内形成段塞流，进而产生严重的压力波动，极端情况下将可能威胁海管安全，因此有效预测和控制段塞流是海管油气安全输送的重要挑战［1-2］。

国内外学者先后对严重段塞流的预测和控制开展了相关研究，并提出了基于顶部节流阀进行控制、气举、段塞捕集等方案［3-4］。在实验室内，通常对管道入口压力进行精准测量，将顶部阀门作为控制变量来实现反段塞控制［5-7］。在海洋油气生产过程中，管道放置的环境恶劣不便于直接测量，对于段塞控制，一种可能的方案是使用顶部压力和流量对管道状态进行估计，再进行反段塞控制，但这种观测方法稳定性不足［8］。JAHANSHAHI 等［9-10］提出了虚拟计量方法估计管道段塞流状态，建立了海管内流体质量守恒的动态常微分方程（ODE）模型，采用海管底部压力以及顶部流量进行控制。海管及其内部的段塞流可视为非线性动态系统，目前通常采用实时滤波方法来进行状态估计。如扩展卡尔曼滤波（EKF）、粒子滤波（PF）等。尽管这些方法应用于非线性系统状态估计已经得到了学术界和工程界的认可，但海管段塞流的强非线性会造成这些方法的整体特性被局部特性所代替，进而影响预测结果的稳定性差［11-14］。一些学者也提出了改进方法，如MEGLIO 等［15］提出了一种非线性Luenberger 型观测器来预测海管段塞流，尽管改善了预测结果的稳定性，但仅适用于阀门小开度的情况。

为了改善对非线性问题的滤波效果，JULIER等［16］提出了采用基于Unscented变换的UKF方法。该方法在非线性滤波方面效果比EKF，PF 的稳定性更好、计算成本更低［17-18］。同时，近年来神经网络开始应用于系统状态估计，特别是小波神经网络（WNN）拥有良好的函数逼近能力、收敛速度和容错能力，在系统急剧变化时具有良好的时频分辨性能［19-20］，可以在模型上很好地近似于系统的动态特性［21］，其在预测与控制领域都有成功的应用［22-28］。本文提出结合基于UKF-WNN 混合模型的状态估计方法，来预测具有强非线性的海管段塞流。推导了海管段塞流ODE 模型，并验证其实际可行性，在此基础上设计了控制器和观测器，提出了UKF 和WNN 混合状态估计方法，可得到海底管道压力和段塞流状体的估计值，并进行了方案验证。本文提出的方法对改善海管段塞流的预测和控制精度，保障海管安全具有一定的理论和实践意义。

1 海管气液混输ODE 模型

为了对海管气液混输过程的段塞流进行预测控制研究，本文首先采用ODE 方法建立海管气液混输物理模型，如图1 所示。模型中的海管包括：海底水平管道、海底下倾管道、水中立管和平台水平管道。

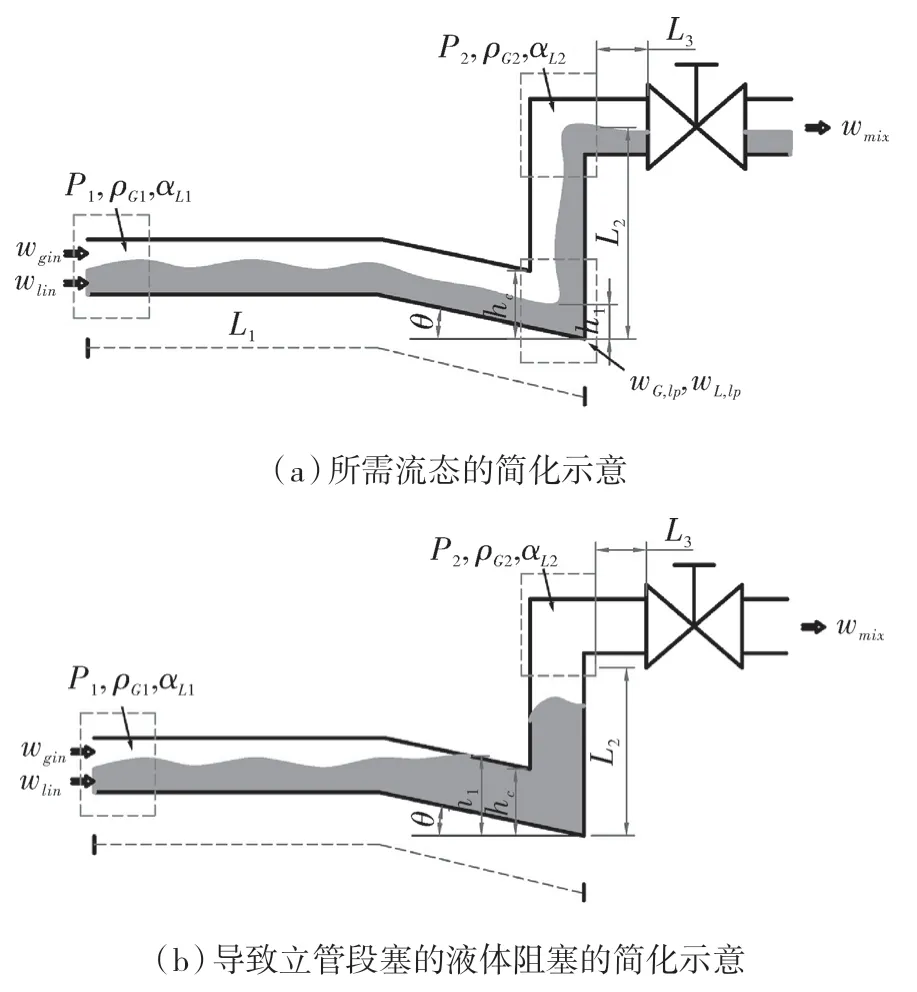
图1 海管气液混输模型及其关键参数Fig.1 Offshore pipeline gas-liquid hybrid mode and its critical parameters

根据质量守恒原理，建立海管各段的液混输的状态方程为：

式中，mG1为海底管道气体质量；ωG，in，ωL，in分别为海管入口的气体和液体质量流量；ωG，lp，ωL，lp分别为立管底部的气体和液体质量流量；ωG，out，ωL，out分别为海管出口的气体和液体质量流量；mL1为海底管道液体质量；mG2为立管内气体质量；mL2为立管内液体质量。

1.1 入口边界条件

根据海管流入的气液两相流体质量分数和密度，可得到海管内的液体质量体积分数为：

式中，Kc为修正因子；αLm为液相质量分数；ρL为液相密度；ρG为气相密度；ρL，h为气液交界处的液相密度。

利用流入边界条件，可以得到海管内的平均液相质量分数为：

结合上式可得海管内平均液体体积分数为：

式中，P1，sta为入口稳态压力；MG为气体质量；R 为常数；T1为温度。

1.2 出口边界条件

海管到达海上平台后，其外部边界压力恒定（分离器压力），在本文中使用定压条件和节流阀模型作为海管出口的边界条件，即：

式中，ωmix为混相质量流量；Cp为常数；f（z）为阀门的开度方程，z∈（0，1），在仿真模型中假设阀门开度为线性，即f（z）=z。

则气体与液体流出的方程为：

1.3 海管模型

海管内的气液体分布不均，其中液体的质量为mL1=，在立管底部海管液位最低点可定义为≅。如果海管内液体质量增加，立管底部的液位也会发生变化，其位置变化有如下关系：

式中，Kh为液位变化的修正因子；hc为初始液位。

因此，海管中液体液位h1可以表示为管道中液体质量mL1的函数：

式中，mL1为模型的状态变量。其他参数均为常数。

海管中气体所占的体积为：

海管气体密度为：

海管入口压力为：

1.4 立管模型

立管总体积为：

式中，r2为立管半径；L2，L3分别为立管顶部和常规管段的长度。

立管中气体体积为：

立管顶部气体密度为：

式中，mG2为立管顶部气体质量；VG，2为立管顶部气体体积。

根据理想气体方程，立管顶部压力可表示为：

立管中液体的平均体积分数为：

式中，mL2为立管顶部液体质量。

立管内平均密度为：

立管内压力损失为：

1.5 立管底部气体流动模型

当液体高度超过临界液位（h1＞hc）时，立管底部将发生段塞，此时的气体流速为0，即：

当立管底部不发生段塞（h1＜hc），气体从体积VG1流入VG2的质量流量为ωG，lp（kg/s）。根据物理模型，决定气量的2 个最重要参数是低点压降和开口面积。表明气体的流动可以近似由阀门流动模型代替，阀门的开度与流量之间的关系，基本上呈线性比例变化，由于气体的可压缩性，当气体密度增大时，阀门的流量也随之增大，其中气体通过的开孔面积为AG。则有：

1.6 立管底部液体流动模型

类似气体方程，立管底部液体的流动方程为：

2 基于UKF-WNN 混合模型的预测控制方法

2.1 预测控制系统

本节将前述的ODE 模型用于观测器和控制设计。如图2 所示，通过观测器来估计系统的状态变量，并将估计值用于状态反馈。首先，用设计状态反馈控制器来稳定系统；然后，通过用观测器提供的状态估计值代替状态x，获得输出反馈控制器。

图2 反馈控制方框Fig.2 Feedback control block diagram

2.1.1 控制器结构

如图2 中使用估计的状态来应用完整的状态反馈。此外，为了防止偏离工作点，通过对估计水下压力Pin的设定点偏差进行积分，增加了积分作用。总控制动作可表示为：

式中，Kc为通过求解黎卡提方程计算得到的线性最优控制器，Ki为相对较小的积分增益。

2.1.2 观测器结构

观测器将UKF 和WNN 相结合，使用顶部压力P2、出口流量w 与顶部阀门开度u 来预测管道入口压力P1，预测值与控制器相结合以稳定系统，其结构如下：

（1）无迹卡尔曼滤波（UKF）结构。

使用UKF 进行状态估计，本系统的状态空间表述为：

式中，vk-1为均值为零的高斯随机噪声，表示模型误差和干扰；wk为高斯零均值测量噪声。

（2）小波神经网络（WNN）设计。

WNN 利用小波元代替神经元，不改变神经网络结构。如图3 所示，本文利用小波网络良好的拟合能力提高海管段塞流估计和预测的能力，在实际训练网络时，使用海底传感器可用时的数据，即完整数据包含P1，P2，w 与u。使用P1（k-1），P2（k），w（k），u（k）作为输入，P1（k）作为输出，对神经网络进行训练。整个映射关系可以表示为：

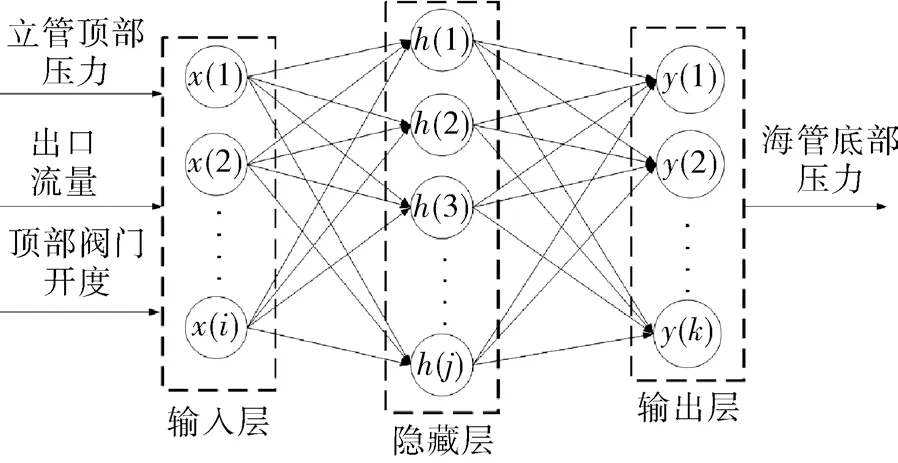
图3 小波神经网络结构Fig.3 WNN structure

（3）UKF-WNN 混合模型算法。

k-1 时刻系统状态为：

①确定Sigma 点与权重：

设随机变量x～（μ，δ），无迹卡尔曼滤波一般取2n+1 个Sigma 点，其中n 为状态变量维度。

其中，λ=α2（n +k ）-n。

在UKF 算法中只需要指定α，κ，n 3 个常数即可，本文中α=1，κ=1，n=4。对于第1 个Sigma 点权值为：

第1 个方差Sigma 点权重为：

剩余2n 个Sigma 点权重为：

②预测系统状态：

③更新系统状态：

④更新卡尔曼增益系数和协方差矩阵：

⑤海管压力P1（k-1）预测：

⑥将P1（k-1），P2（k），w（k），u（k）输入WNN，得到P1（k）：

3 方法验证及分析

图4 所示为现场试验系统示意。海底管道长度为5 000 m，倾斜角度为15°。立管的高度为30 m，顶部安装有节流阀。井口采油树连接海管，在入口处使用多相流量计分别测得气相和液相的流量。采集数据分别为管道入口压力P1、顶部阀门开度u、立管顶部压力P2与出口流量wout。在初始时刻打开控制器，阀门开度为10%，使用3 种不同的观测方案对系统进行状态估计。不同观测方案下系统真实值和估计值之间的均方误差。试验数据和结果分别见表1，2。

表1 模型初始参数Tab.1 Model initial parameters

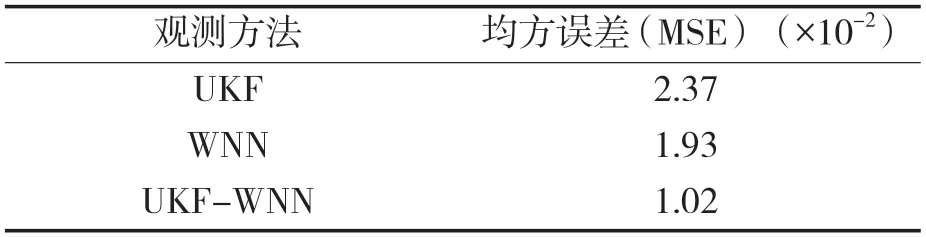
表2 不同观测方法均方误差Tab.2 Mean square error of different observation methods

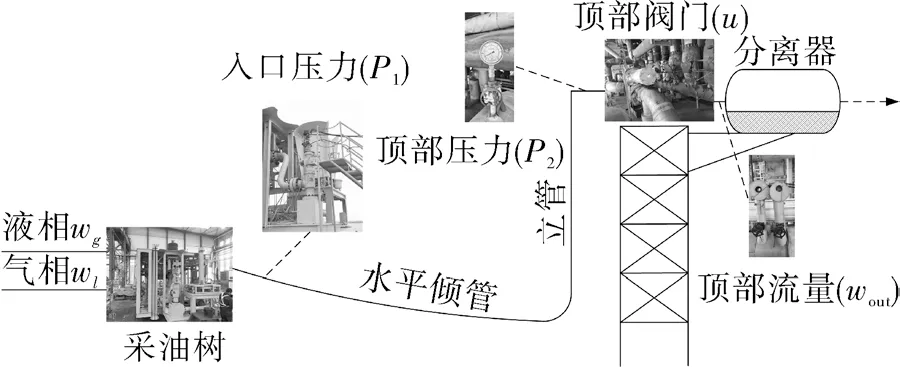
图4 现场装置示意Fig.4 Schematic diagram of the experimental device on site

不同方法的状态估计结果如图5 所示。由图中可以看出，在一定范围内3 种观测方法均能够实现对入口压力的估计，但使用UKF-WNN 混合模型的观测方案可以得到更加精确的预测效果。其均方误差相较UKF 和WNN 分别降低了44%，47%。然而，当顶部阀门开度增加时以及系统输入扰动较大时，对底部管道压力的状态估计会变得困难，而观测器的预测精度将会影响到系统稳定。将顶部阀门开度逐步增大并且添加入口流量噪声，再次进行状态估计和段塞流控制，其结果分别为图6，7，不同观测方法在不同阀门开度下的估计均方误差见表3。

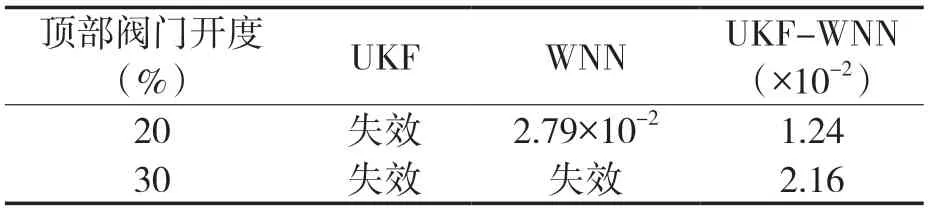
表3 不同估计方法在不同顶部阀门开度下的均方误差Tab.3 Mean square error of different estimation methods with different top valve opening

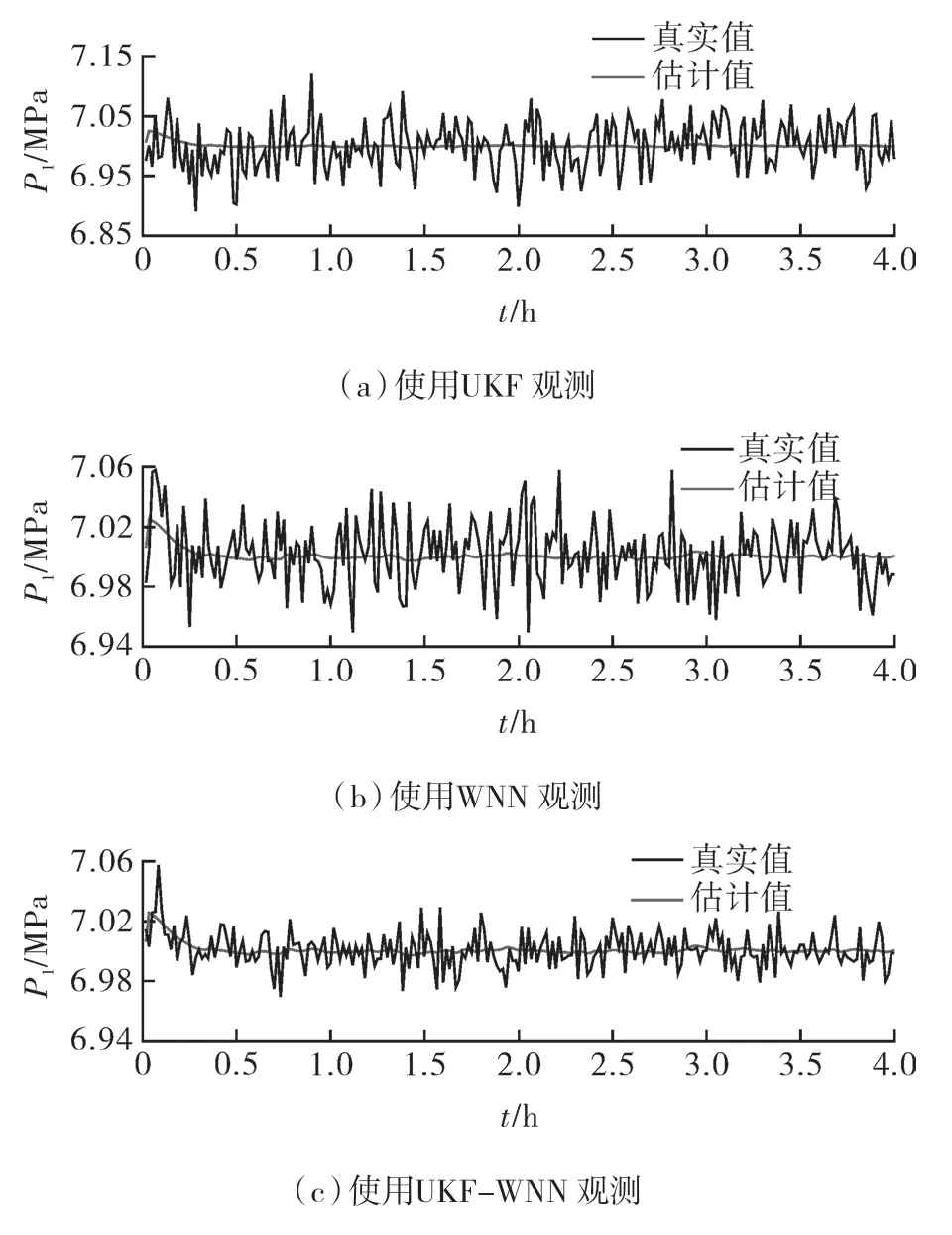
图5 不同方法的状态估计结果Fig.5 State estimation results of different methods

图6 不同观测器的控制结果（顶部阀门开度20%）Fig.6 Control results of different observers（top value opening 20%）

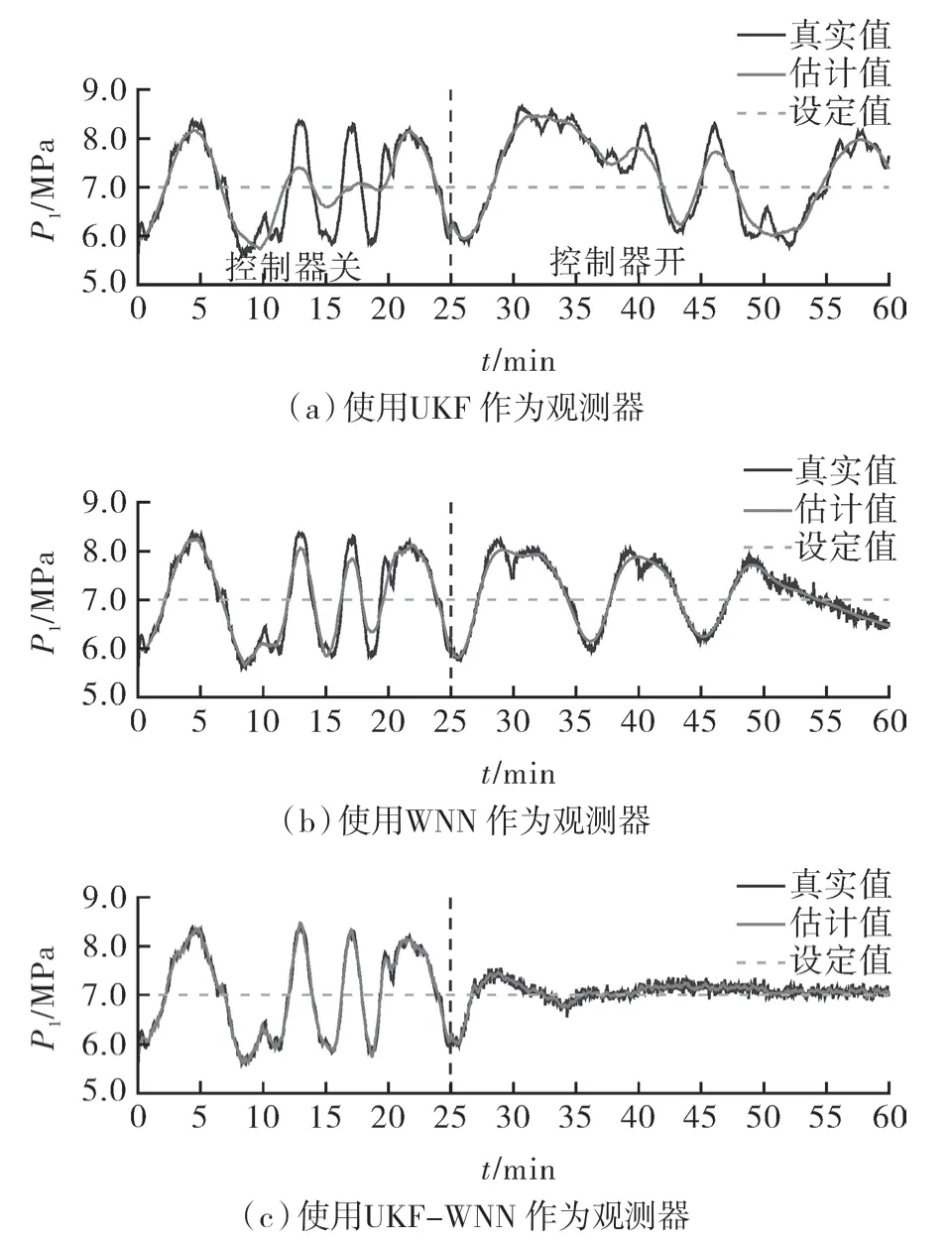
图7 不同观测器的控制结果（顶部阀门开度30%）Fig.7 Control results of different observers（top value opening 30%）

从表中可以看出，UKF-WNN 方案，在系统输入存在干扰的情况下依旧能够为控制器提供较为精确的估计值，使得系统达到稳定。而在20%阀门开度的情况下，UKF 不能准确预测压力值，导致控制系统失效，而WNN 虽然能够稳定系统，但是均方误差相较UKF-WNN 增大了125%。并且WNN 在阀门开度达到30%时，也失去了有效性。传统的观测器对于系统输入变动时其跟随能力较弱，WNN 虽然对系统波动的灵敏度更高，但UKFWNN 估计值更为准确，抗干扰的能力更强，实际值与设定值的均方误差明显更小，系统整体表现的更为平稳。

4 总结

（1）基于相质量守恒定律，建立了海管气液混输ODE 模型，充分结合了UKF 和WNN 的优点设计了控制器与观测器，并采用现场试验进行了方法验证。

（2）本文提出UKF-WNN 混合模型能够较好地拟合顶部压力、流量与阀门开度同底部压力的关系，其均方误差相较UKF 和WNN 分别降低了44%，47%。

（3）UKF-WNN 混合模型很好地改善了海管段塞流状态估计精度，提高了海管段塞的控制效果。在系统输入存在干扰的情况下依旧能够为控制器提供较为精确的估计值，使得系统达到稳定。