流体机械转子系统非线性振动机理研究

张振杰，赵金月，常学森，刘爱玲，姚权桐，高攀龙

（1.辽宁科技大学 机械工程与自动化学院，辽宁鞍山 114051；2.辽宁科技大学 创新创业学院，辽宁鞍山 114051；3.合肥通用机械研究院有限公司，合肥 230031）

0 引言

在离心泵、风机、汽轮机等流体机械中，机械性能很大程度上取决于转子系统的稳定性［1-2］。准确预测转子系统的振动特性对于流体机械的正常运行具有重要意义，目前相关研究人员主要运用有限元软件预测转子的振动特性［3］。

随着转子转速增大，流体机械转子系统的非线性振动特性变得越来越明显。然而，常用的线性化分析方法无法解释这种非线性振动现象［4］，近年来，越来越多的研究人员开始关注用数值方法，计算转子系统的非线性振动特性［5］。

非线性转子动力学的研究始于20 世纪90 年代，MUSZYNSKA 等［6-7］结合大量转子试验结果，提出了非线性液膜激振力计算模型，该模型中存在可以将液膜整体运动特征表征的关键量γ，转子的8 个动力学系数均由γ计算。基于非线性油膜力模型，DING 等［8］提出了转子-密封系统的非线性密封力模型，模拟了转子系统的振动特性。基于非线性密封力模型，CHENG 等［9］提出了转子-密封-轴承系统振动模型，探索了不同的转子动态特性参数对转子轴线轨道的影响。

随着转子-密封-轴承系统模型的不断完善，CHENG 等［10］建立了基于Muszynska 非线性流体力模型和非线性油膜力的转子-密封-轴承系统模型。侯峰等［11］搭建了冷压缩机转子轴心轨迹测试系统，通过试验测试了滑动轴承转子轴心轨迹图。周文杰等［12］基于转子Jeffcott 理论，提出了一种双盘转子密封系统非线性模型，分析了双盘转子密封系统的非线性振动特性。翟璐璐等［13］以多根轴的转子轴系为研究对象，建立了齿轮-转子-密封-轴承系统的非线性振动动力学模型。

目前针对转子系统的研究多集中于软件模拟，相关转子试验研究相对较少，研究内容大多是对现象的分析，不同因素对转子系统振动特性影响的讨论较少。针对以上问题，本文应用Muszynska 非线性密封力模型和非线性轴承油膜力模型［14］发展了非线性转子-密封-轴承振动模型。采用四阶龙格-库塔偏微分法［15］求解非线性运动模型的控制方程。搭建了转子-密封-轴承系统试验平台，从试验和模拟两方面分析了不同转速下的轴心轨道图变化规律。同时探讨了转速、结构参数和轴承尺寸等不同影响因素对转子系统振动特性的影响，给出了不同参数对转子振幅的影响规律以及影响优先级顺序，为进一步的优化设计提供理论基础。

1 非线性转子动力学理论基础

1.1 转子-密封-轴承系统的非线性运动方程

双支撑转子-密封-轴承系统可以简化为带有单盘系统的Jeffcott 转子［16-20］，如图1 所示。密封处的附加质量可以简化为刚性盘，转轴可以简化为一个没有重力且具有一定弹性的转子。

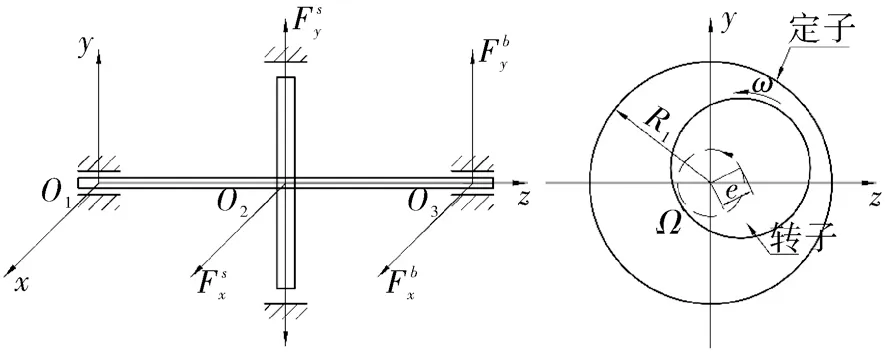
图1 转子-密封-轴承系统示意Fig.1 Schematic diagram of the rotor-seal-bearing system

1.2 非线性密封力模型

对于非线性转子系统，密封处的流体力沿流动方向呈周期性变化，这种变化可引起流体惯性力的增加。在转子振动过程中，惯性力的影响不容忽视，因此用流体圆周的平均速度与转子角速度的比值γ来反映油膜惯性力的运动规律。Muszynska 非线性密封力模型［6］描述如下：

其中ε=（x2+y2）0.5/C1，γ=γ0（1-ε）n2

Ks=K0（1-ε2）-n1，Ds=D0（1-ε2）-n1

式中，Ks为流体刚度系数；ms为密封位置处转子的质量［9］；ε为偏心率；x，y 为转子在x，y 方向的位移，即转子的坐标；C1为密封间隙；n1，n2，γ0为常系数，取值与密封结构有关，光滑密封取值范围为0.5＜ n1＜3，0＜n2＜1，γ0＞0.5；K0为等效刚度；Ds为流体阻尼系数；D0为等效阻尼。

1.3 非线性轴承油膜力模型

轴承也是转子系统的重要组成部分，考虑到轴承尺寸，以短轴承的非线性油膜力模型为基础，建立转子系统的非线性运动模型。油膜力模型的无量纲形式如下［14］：

1.4 转子非线性运动模型

基于Muszynska 非线性密封力模型方程（1）和非线性轴承油膜力模型方程（2），建立转子-密封-轴承系统非线性运动模型如下：

式中，md为密封处转子的质量；ke为转子刚度；ω为弧度制下的转速；mb为轴承处转子的质量；t 为时间。

转子系统非线性动态特性响应的计算流程如图2 所示。采用四阶龙格-库塔法求解非线性偏微分方程［15］。

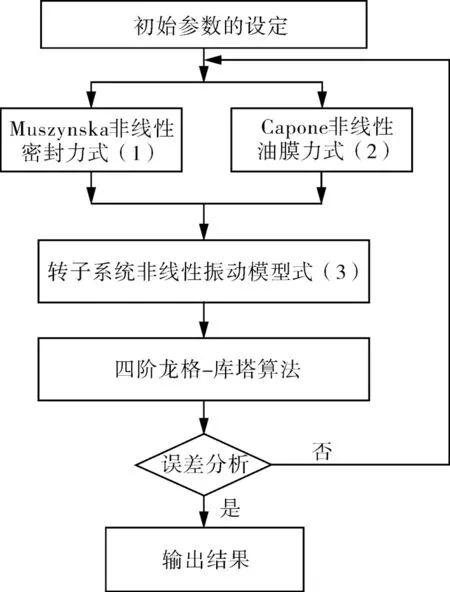
图2 计算流程Fig.2 Block diagram for nonlinear computation

四阶龙格-库塔法的收敛精度随着时间积分步长的减小而提高。根据模型的特点，采用固定时间积分步长Δt 进行计算。综合考虑计算时间和结果的影响，Δt 设定为π/100；误差精度设置为0.000 1［12］。

2 结果与讨论

基于建立的理论模型，本节对计算结果进行讨论，几何参数和操作条件见表1［12］。

2.1 转子轴心轨迹图试验

基于转子非线性振动的特点，搭建了转子轴心轨迹测试平台。用1 台外接增压泵向转子间隙处供压，转子电机为1 台高速变频电机。为平衡轴向力，密封口环转子和定子对称布置，并由压力表测环形腔体内的水压。试验时，高压泵通过入口将额定压力的水压送到定子架与转子形成的环形腔体中，然后有压水再由环形通道流过定子与转子处的密封口环间隙到泄水室中，泄水室通过管路将试验台内部的水导出到外接开式水箱中，待压力表数值基本稳定，达到额定压差时，即可测量。而转子轴心轨迹可由安装在密封口环卡套处正交90°布置的1 对非接触式位移传感器测量。为保证精确性，在左右2 个卡套处分别布置2 对传感器，最终测量两端信号的平均值。

测试系统包括CZ600 位移传感器、AVANT MI-7016 采集分析仪以及控制电脑，转子轴心轨迹图可由非接触式位移传感器直接测得。

图3 示出2 000 r/min 转速下转子无量纲轴心轨迹振动，随着压强的提高，密封间隙处的洛马金效应变得更加明显，液膜的支承作用增强，转子的振幅反而下降，在0.5 MPa 工况时，转子的振幅最大，接近0.01。并且，压差越小，转子的轴心轨迹越接近圆形。

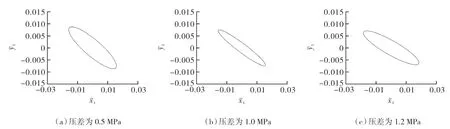
图3 2 000 r/min 转速时不同压差下的轴心轨迹Fig.3 The axis orbit diagram at 2 000 r/min under different pressure differences

2.2 转速对转子系统振动特性的响应

基于试验分析结果，进一步分析了其他工况下的转子轴心轨迹，为了保证转子轴心轨迹更接近圆形，模拟压强均小于0.3 MPa。图4（a）示出转子系统转速在3 000 r/min 时的轴心轨迹。此时的轴心轨迹接近于1 个无量纲半径为0.2 的圆。当转速提高到8 500 r/min 时，轴心轨迹已经从单周期运动变成了倍周期运动，如图4（b）所示。随着转速的进一步提高，当转速接近12 000 r/min 时，转子的周期性进一步恶化，如图4（c）所示。当转速超过15 000 r/min 时，轴心轨迹图已经变为混沌运动，如图4（d）所示。

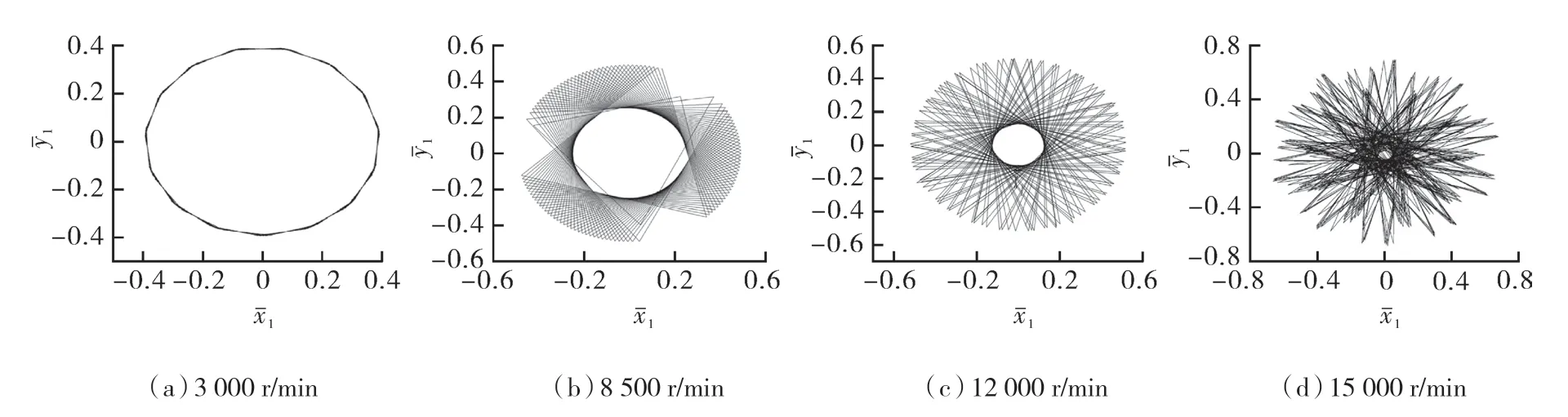
图4 4 种转速下转子轴心轨迹Fig.4 The axis orbit diagram under 4 different speeds

2.3 密封长度对转子系统振动特性的影响

密封长度对转子的振动有明显的影响。图5模拟了密封长度从0 增加到0.1 m 的过程中转子的分岔。从结果中发现转子的无量纲幅度先保持静止，然后随着密封长度的增加而增加，这意味着转子非线性振动中存在临界密封长度，而且临界密封长度随着转速的增加而减小。

图5 密封长度分岔Fig.6 The bifurcation diagrams of the seal length

2.4 密封间隙对转子振动特性的影响

图6 示出了转子系统在1 000，3 000 r/min 转速下的密封间隙分岔。随着密封间隙的增大，转子系统的无量纲幅度先减小，当密封间隙大于0.3×10-4m 时，密封间隙对转子系统振动的影响可以忽略不计，可见，密封间隙的大小与转子振幅成正比。

图6 密封间隙分岔Fig.6 The bifurcation diagrams of the seal clearance

2.5 轴承润滑长度对转子振动特性的影响

轴承对转子系统的非线性振动特性也有显著影响，转子的稳定性随着轴承支撑刚度的增加而增强，轴承的支撑刚度主要与润滑结构和润滑介质有关。本文探究了润滑结构中的长度对转子振动响应的影响。轴承润滑长度的分岔如图7 所示。随着密封长度的增加，转子的无量纲幅值随着轴承润滑长度的增加而减小。当轴承润滑长度接近0 m 时，转子的无量纲振幅达到1。基于滑动轴承方程（2）的油膜力模型，油膜力随着轴承润滑长度的增加而增加，导致支撑刚度的增加。转子的稳定性与支撑刚度成正比，增加轴承润滑长度可以减小无量纲幅值。

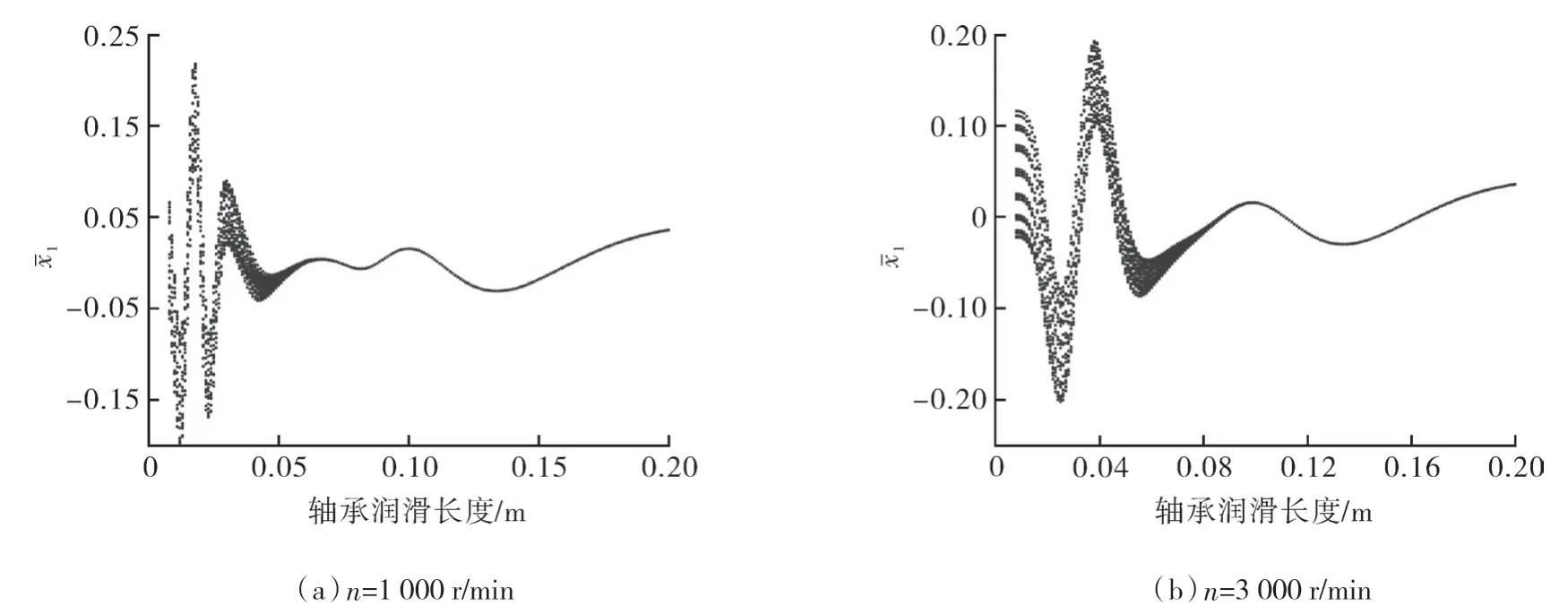
图7 轴承润滑长度分岔Fig.7 The bifurcation diagrams of the bearing lubrication length

3 结论

（1）基于Muszynska 非线性密封力模型，建立了转子-密封-轴承系统的非线性运动模型。运用四阶龙格-库塔法求解了转子-密封-轴承系统的非线性运动方程。

（2）在压强为0.5 MPa 下，洛马金效应明显增强，密封处的液体会对转子起到明显的支承作用，同时压强越小，转子轴心轨迹越接近圆形。

（3）转子在3 000 r/min 增大到12 000 r/min的过程中，轴心轨迹由半径为0.4 的圆形逐渐变为成倍周期图型，当转速超过15 000 r/min 时，转子的振动变成混沌状态。

（4）从转子分岔图中发现，转子系统的振幅与转速和密封长度成正比，与密封间隙和轴承润滑长度成反比。因此，通过增加密封间隙或延长轴承润滑长度的方式以降低振幅。

（5）在影响转子振幅的参数中，对转子系统影响最大的是转子转速，其次是转子结构。