基于秩亏法处理地表形变监测数据平差的设计

□□ 陈俊祺,上官凯林,刘会芳 (武警山西总队参谋部,山西 太原 030012)

引言

变形监测外业工作时会遇到各种复杂的情况。由于被监测地物不断变形的特殊性质,在其附近较难找到稳定的工作点。要在被监测地物附近建立基准点和工作点组成首级网[1],然而这个基准点可能和监测物一样存在变形,且可靠性尚未可知。最终数据是点位高程而非观测值高差,可将点位高程设置为参数,采用间接平差或者秩亏法平差法进行内业工作。但秩亏自由网法和间接平差各有利弊。在只有一期观测值时,且基准任意的自由网,采用秩亏自由网法比间接平差法工作量大,且在一定条件下二者平差结果相同。但当具有类似变形监测多期观测值时,仍然采用间接平差法,结果受基准点影响较大,可采用秩亏法进行平差[2-4]。

现实生活中的外业工作得到的数据往往是庞大的,目前多采用误差平均分配法进行内业工作。其主要原因是由于采用加权法平差工作量过大。为了提高内业工作质量,迫切需要一种可以处理庞大数据的秩亏平差软件。而目前关于秩亏水准网的平差软件少之又少,大多为算法理论研究。根据文献[5]和文献[6]可知,秩亏法平差大致可以分三类:一类是利用广义逆矩阵理论的Mittermayer伪逆解法;第二类是Mittermayer附加条件法、Pelzer伪观测值法和Perelmuter消去条件法;第三类是通过一定技术将将秩亏自由网平差转化为间接平差的Wolf直接解法。下文将基于第二类附加条件法进行软件的开发。

1 秩亏自由网平差原理以及数学模型

1.1 间接平差

设t为必要观测值,n为观测值数目。间接平差的函数模型见式(1):

(1)

(2)

将式(2)代入式(1)见式(3):

l=L-(BX0+d)=L-L0

(3)

式中L0为观测值的近似值矩阵,l为误差方程常数项,也就是观测值与其近似值之差,因而可以推导出误差方程矩阵见式(4):

(4)

式中:V——观测值改正数。

假设权阵为P,则平差的准则见式(5):

VTPV=min

(5)

(6)

将最后一项转置后见式(7):

BTPV=0

(7)

将式(4)带入式(7)见式(8):

(8)

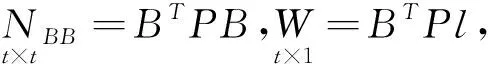
(9)

式(9)中系数矩阵NBB为满秩的非奇异矩阵,可以求得唯一解,这就是间接平差函数模型求解方法[7]。

1.2 秩亏自由网平差法与附加条件法

附加条件法的基本思路是:用间接平差法平差自由网时,由于网中没有足够的起算数据,所以法方程系数矩阵NBB秩亏。设秩亏数为m,添加m个参数条件的限制方程,可按照附有限制条件的间接平差解算方法进行解算。条件方程见式(10):

(10)

式中:S——参数限制条件方程系数矩阵;

x——参数改正值;

u——参数个数。

限制条件方程应与法方程线性无关,这一要求等价于关系式(11):

(11)

限制条件方程中的方程式也与法方程线性无关。所以S矩阵的秩为m。利用拉格朗日乘数法求偏导数,然后得到法方程(通过联立参数限制条件得到法方程组),最终得到计算秩亏自由网最优解,见式(12):

(12)

其单位权中误差见式(13):

(13)

式(13)中根号下分母应不为0,否则使用软件计算时容易出错,即出现单位权中误差无穷大的情况,从而导致在Matlab编程时协因数阵元素全部为INF(在Matlab中INF为无穷大)。对于秩亏水准网来说,秩亏数为1,根据平差后所有高程点的改正值之和为0,列出条件方程见式(14):

(14)

因而对于秩亏水准网来说,S的具体形式见式(15)[7]:

(15)

2 程序需求分析

随着我国社会的不断发展,高层建筑不断出现,民用设施不断完善更新,人们对于开采业安全性的需求不断提升,变形监测的应用也越来越广泛。然而变形监测的数据是多期观测的大量数据,人工解算效率低下且易出错,已经不适应当代发展的需求。外业一般得到的原始数据有起点和终点点号、观测数据、路线长度等。根据式(12),计算改正值所需要的矩阵分别为误差方程系数矩阵B、权阵P、附加条件系数矩阵S以及误差方程常数项l等四项,所以代码编写的主要任务是从外业的原始数据得到解算参数改正值的所需矩阵。

3 程序设计与集成

3.1 程序结构

软件主要结构为:数据读取与导入模块、数据分类以及调用模块、数据运算模块以及保存和清除模块,软件主要实现步骤如图1所示。

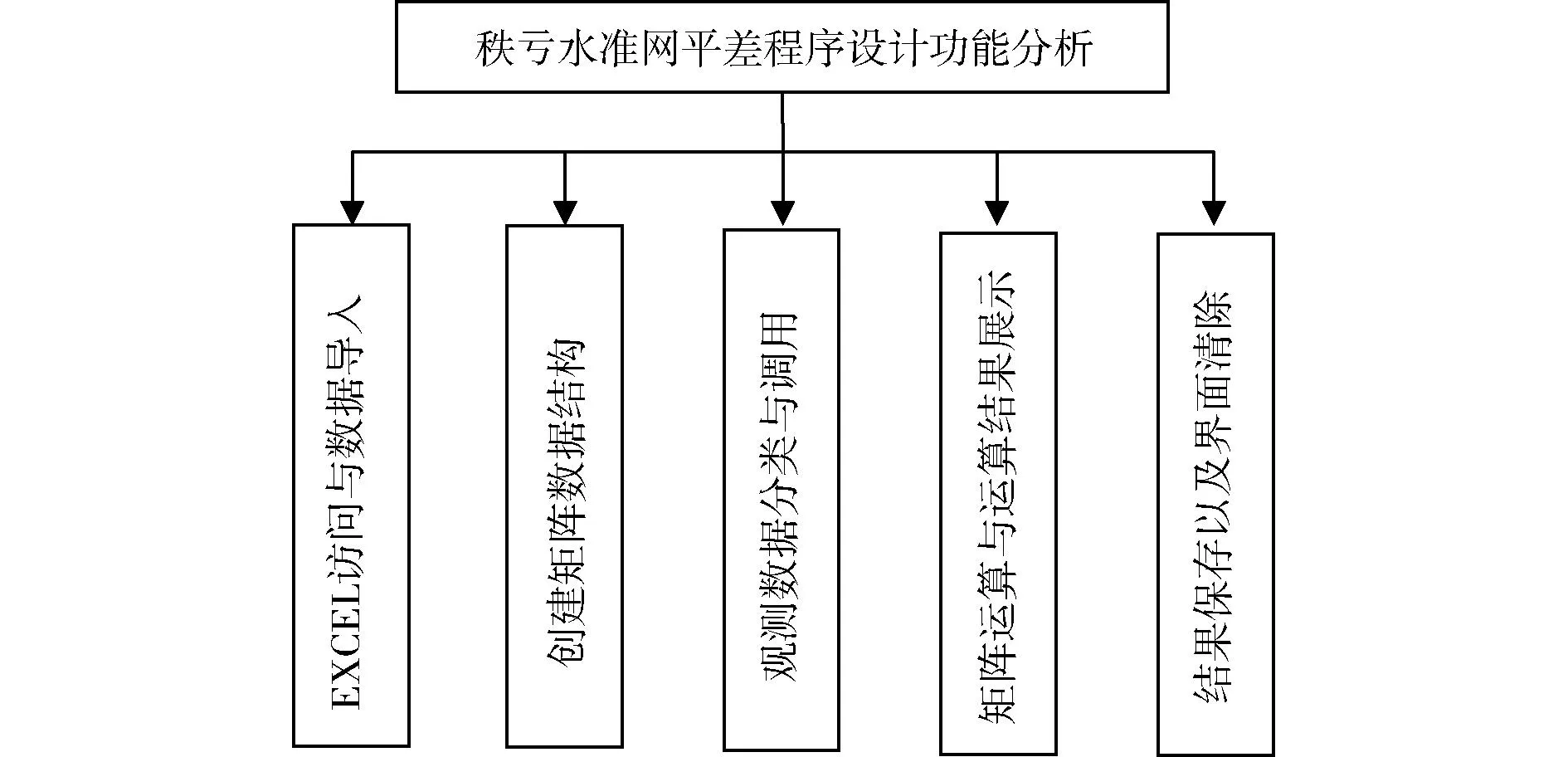
图1 软件实现步骤

3.2 数据结构

在Matlab访问以及将Excel数据表格的点号、路线长度以及观测高差放置在原数据矩阵中,以原数据矩阵的列向量为单元,对数据进行分类,分别对起点、终点、观测高差以及路线长度以不同的变量命名,以方便调用。

3.3 关键算法

3.3.1提取误差方程系数矩阵

误差方程系数矩阵B中元素只有0、-1和1,而且矩阵的每一行有且仅有一个“1”和一个“-1”,其他元素均为0。当每一行的列号所对应的点号是终点时,这个元素应为“1”,当为起点时,这个元素应为“-1”,否则为“0”。这样就可以由起点和终点提取出误差方程系数矩阵B。

先定义系数矩阵B为一个零矩阵。然后找出每行起点和终点点号对应的列号,并分别赋值-1和1,检索原数据矩阵的起点和终点点号。假设:I为原始数据矩阵,I[1,1]代表矩阵I的第一行第一列,n为数据行数,系数矩阵流程如图2所示。

图2 系数矩阵提取流程

3.3.2提取权阵

水准路线定权和路线长度有关,可依据此来定权。

3.3.3提取附加条件系数矩阵

由秩亏水准网平差参数改正值之和为0,可以推导出附加条件系数矩阵为式(7),直接定义即可。

3.3.4提取误差方程常数项

式(3)中B已经提取出,X0是各个点的参数估计值,如果给出,则可以直接计算。当导入数据后,发现未给出参数估计值,可以通过给出假定起算点高程值来进行参数估计值赋值,假设参数估计值矩阵为X。

参数自动赋值编程是假定起点1的高程值为0,并定义一个n行1列的矩阵,然后从起点到终点第一次逐行遍历,只要起点为1,就可以根据高差对终点对应的点号赋值;再从终点到起点第二次逐行遍历,只要终点为1,就可以根据高差对起点对应的点号赋值。这两次遍历方法是一样的,称为第一类遍历。第一类遍历流程如图3所示。

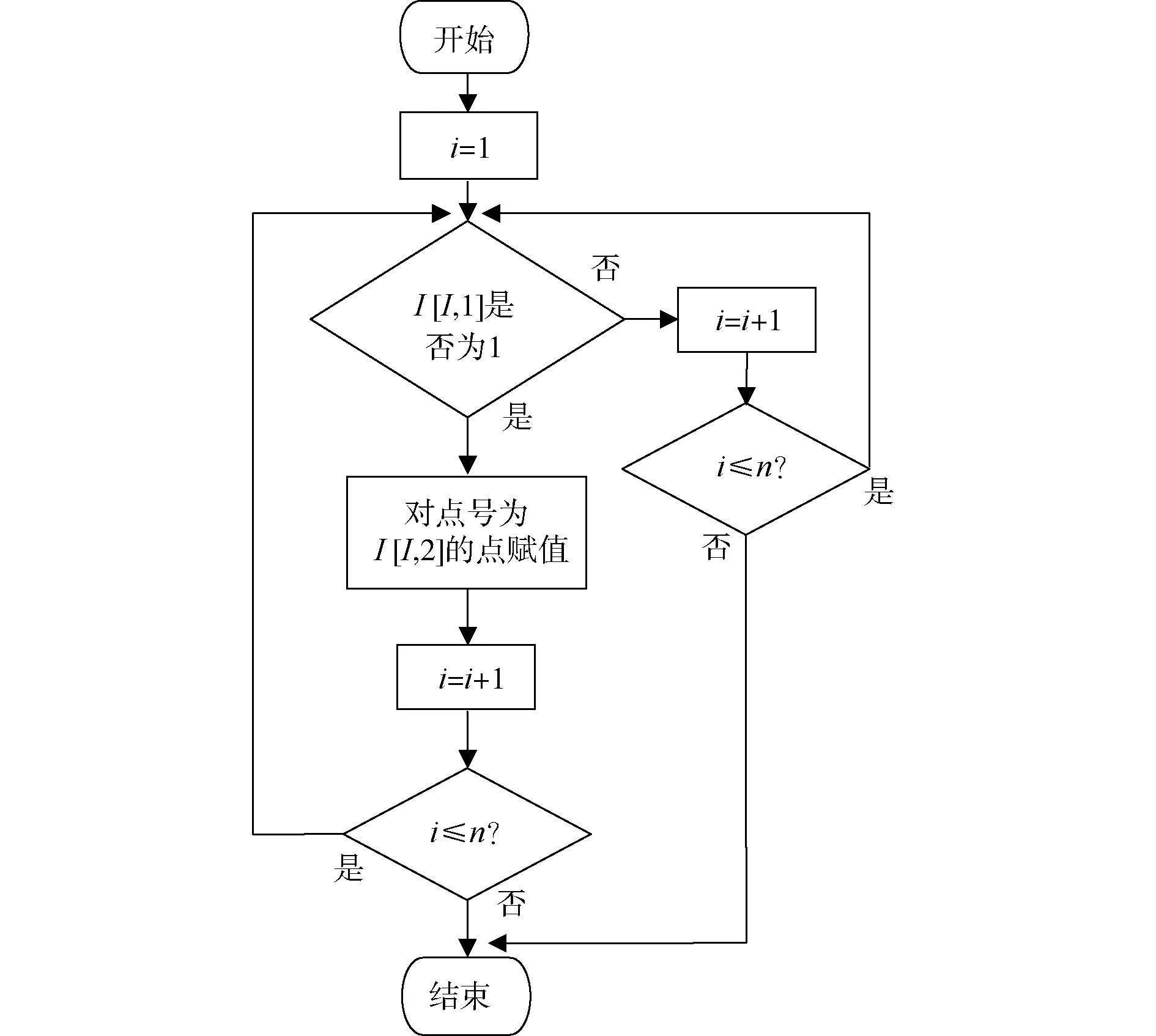
图3 第一类遍历流程

这样完成了赋值的初步工作。由于并不是所有的点都和点号为1的点有关,所以还有一些点仍然未进行赋值,所以需要下一步工作。从起点到终点进行第三遍遍历。依次判断每一行的起点、终点和高差进行判断,判断条件为:起点参数估计值不为0;起点点号不为1;终点参数估计值为0。若都满足,根据两点高差和起点参数估计值对终点参数估计值进行赋值。这样就完成了第三遍遍历。

在经历多组数据测试以后。发现第三遍遍历在水准网较为复杂时会出错,具体原因是正向遍历并不能完成所有点的赋值,还需要进行一遍反向遍历,可将所有点的参数估计值都完成赋值,所以需要进行第四次反向遍历,判断条件为:终点参数估计值不为0;终点点号不为1;起点参数估计值为0。若都满足,可以根据观测值和终点点号对应的参数估计值对起点进行赋值。第三次和第四次遍历是相似的,称为第二类遍历。这样就完成了赋值工作。当然,程序还有许多需要正反遍历进行赋值以及计算工作,方法和X0的赋值基本类似。第二类遍历流程如图4所示。

图4 第二类遍历流程

4 程序测试

在GUI界面和运算代码编写完成之后,利用Matlab自带的deploytool工具将运算代码和界面代码等打包为可以脱离Matlab独立运行的程序。保存目录中会有一个exe文件,就是设计好的软件界面启动文件,可以创建其快捷方式并放在桌面。这个保存目录是已更改的名字,并不是原名,原名为for-test。打开之后可以进行数据测试工作。

点击导入数据按钮,然后点击计算,就可以得到各种需要的数据,点击保存可以得到结果表。为了验证平差程序的正确性,以文献[3]的数据来进行验算,见表1。水准网示意如图5所示,软件运行平差结果如图6所示,对比文献[3]的平差结果,见表2。

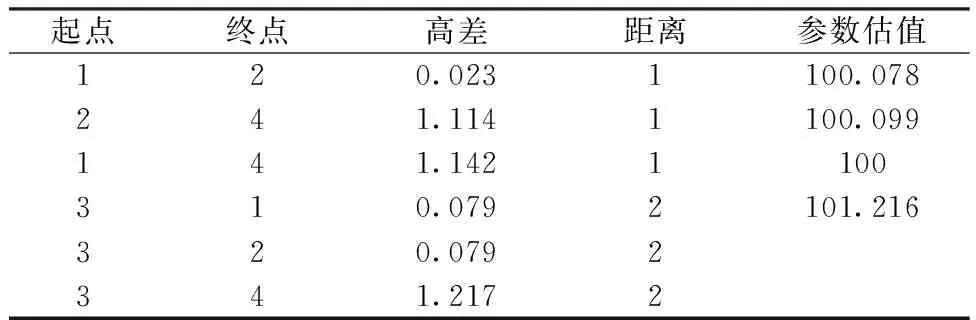
表1 测试数据

表2 对比结果

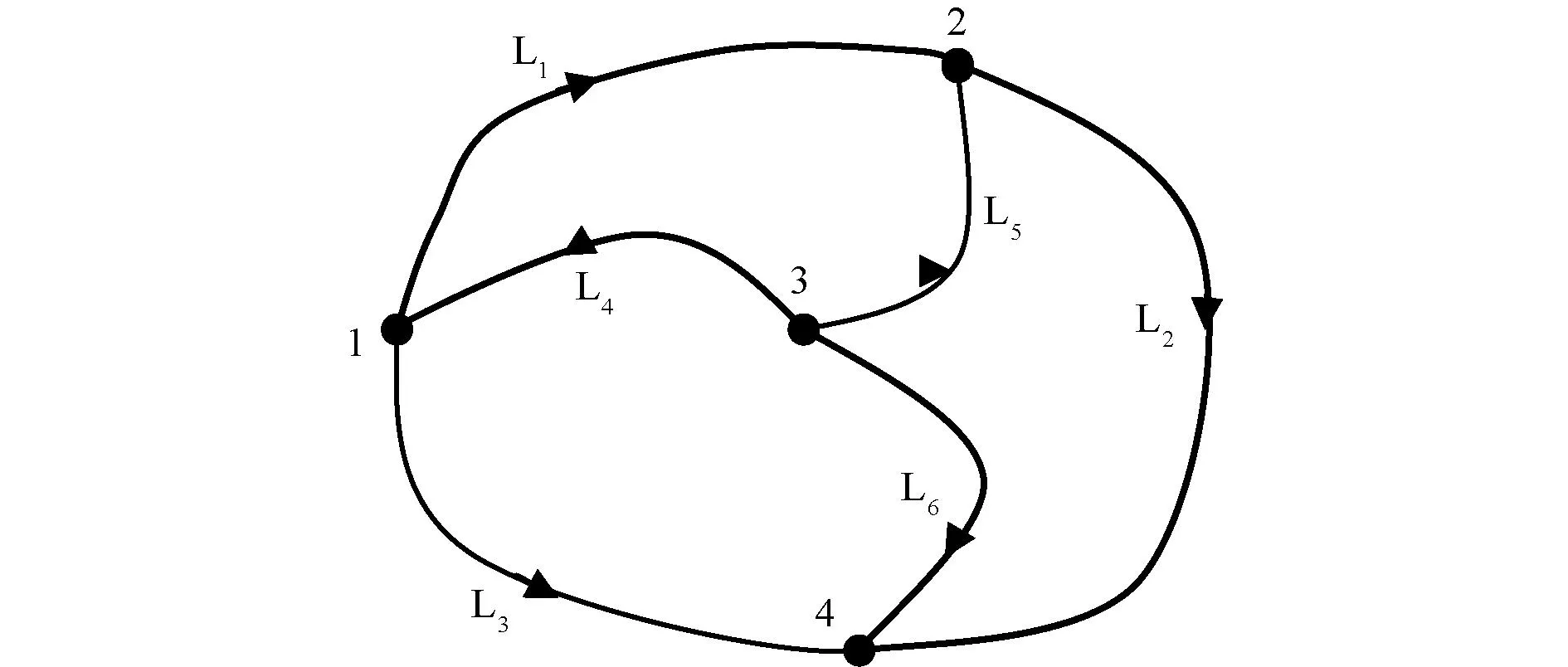
图5 水准网示意图

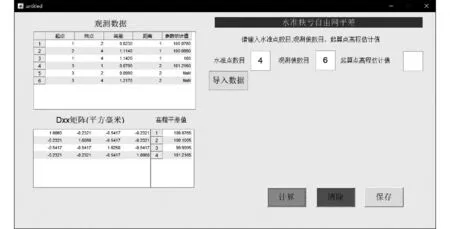
图6 平差结果

由表2可知,1号点和4号点平差结果是有差异的,分别差了0.1 mm,但是总的平差改正值之和是不变的,依然为0。

5 结语

目前对于地物变形监测的主要方法是基于水准的多期观测,数据必然是大量的,并且多采用误差平均分配法进行内业处理,其主要原因是因为通过定权分配误差计算工作量比较大。无论间接平差还是秩亏自由网平差,都需要进行大量的参数估计值赋值工作。利用Matlab开发的程序进行参数估计值赋值工作,极大地减少了变形监测内业计算的繁琐程度。