水下结构物重力基础贯入及抗剪性能有限元分析①

□□ 魏 鑫,刘 炜 (.山西省交通建设工程质量检测中心(有限公司),山西 太原 030006;.山西工程科技职业大学 建筑工程学院,山西 晋中 03069)

引言

在深水海洋油气开发工程中包括大量的水下结构物,如海底管道终端设备(PLET、PLEM)和管汇(Manifold)等,水下生产设施广泛采用重力基础作为永久性基础,重力式基础作为一种浅基础,其抵抗侧向载荷的能力较弱,且容易受到海底流作用而发生冲刷和沉降[1]。采用裙板形式将浅基础贯入到一定深度,可以提高其侧向稳定性,同时对防止海水冲刷也起到一定的作用。水下设施的浅基础上布置型钢或者加强筋可以提高基础的刚度,保证通过吊放下水安装时,吊点可以作用在基础上[2]。国内外相关标准中并未对该类带特殊裙板的重力基础设计做详细的计算描述。有限元方法在水下结构物的基础分析中得到了广泛应用。刘润等[3]对黏土中的筒型基础进行了有限元计算;针对海上风电用筒型基础,詹云刚[4]和丁红岩等[5]采用有限元方法对承载力进行了计算;王明显等[6]、吴景健等[7]和王虎刚[8]对导管架平台的重力基础承载力进行了理论计算和分析;范庆来等[9]对浅基础的承载力,采用复合加载模式进行数值研究;国内对于水下设施浅基础集中于承载力研究,有必要对于贯入特征和侧向稳定性进行详细的理论计算和数值分析,以保证基础的设计可靠性。

1 理论计算

某水下结构物重力基础如图1所示,型钢位于基础以下,可起到部分裙板作用,但是此时受力面积较大,对于贯入要求较高的此类新型浅基础,可能需要加配重或者负压吸力的方式实现贯入。水下设施所在地区的海床表层往下约2.3 m范围内为黏土,表层的土壤抗剪强度为3 kPa,土壤容重为7.5 kN·m-3。浅基础形式如图1所示,长为3.3 m,宽为2.5 m,在长度方向布置了2道300 mm×300 mm的H型钢,在宽度方向布置了3道300 mm×300 mm的H型钢。浅基础裙板的贯入计算可以参考桩的贯入计算,但由于浅基础的深度较小,因而在计算时需要考虑克服其顶部平板承载力的影响。根据API RP 2GEO—2011《Geotechnical and Foundation Design Considerations》[10]中的规定,裙板的贯入阻力包括侧向摩擦阻力和顶部阻力两部分组成,计算见式(1):

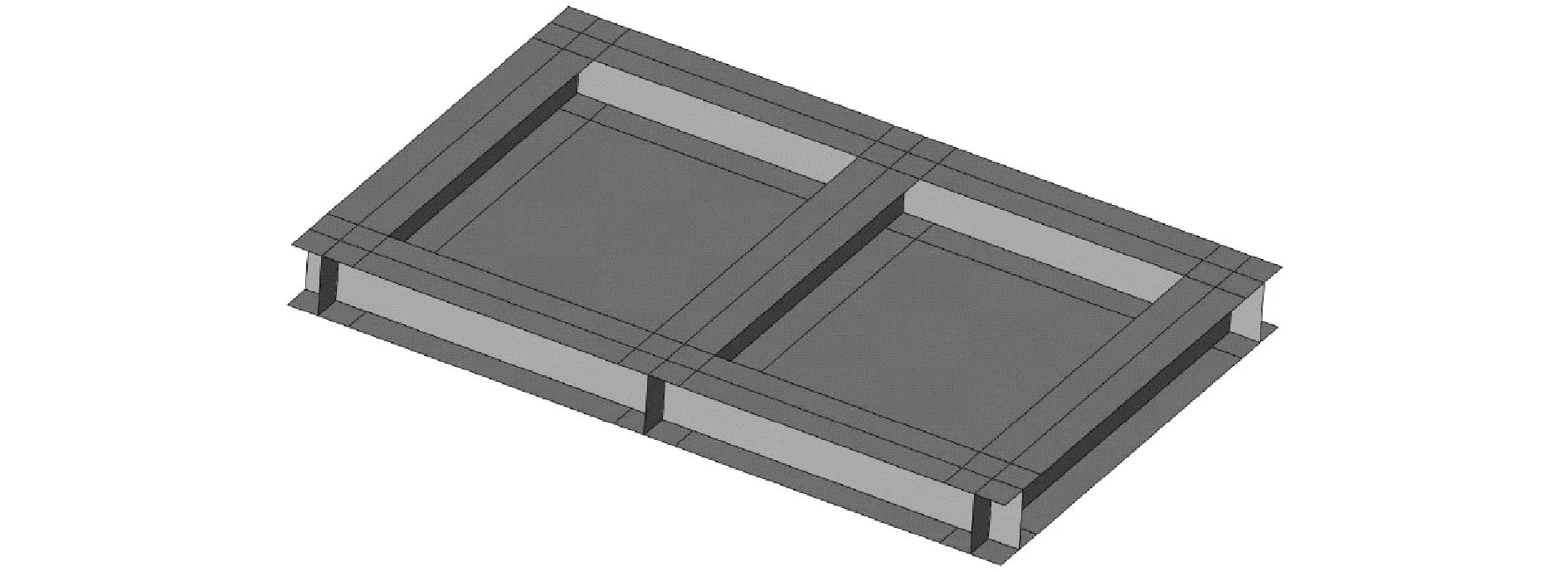
图1 水下结构物重力基础

Qc=Qf+Qp=fAs+qAp

(1)

式中:Qc——极限轴向抗压承载力;

Qf——侧向受压摩擦阻力;

Qp——端部阻力。

侧向摩擦阻力由单轴摩擦力f以及裙板的双向面积As确定,端部承载力由端部阻力系数q和端部面积Ap确定。对于黏土,其单轴摩擦力约等于抗剪切强度;端部承载力系数按9倍的剪切强度考虑。

API RP 2GEO—2011中对于浅基础的承载力计算公式,其中黏土的不排水承载力计算见式(2):

Qd=(suNcKc)A′

(2)

式中:Qd——最大竖向载荷;

su——基础面处的不排水剪切强度;

Nc——无量纲常数,5.14;

Kc——修正系数,包括形状修正系数、嵌入深度修正系数、载荷倾斜修正系数、基础倾斜修正系数、海床倾斜系数等;

A′——水平面积。

经过理论计算得到的型钢贯入阻力、平板承载力以及总贯入阻力值见表1。由计算结果可知,该浅基础贯入时的阻力主要来自于型钢端部阻力和顶部平板阻力。为降低贯入时的阻力,可以减小H型钢的端部面积并在顶板上开孔,可从一定程度上利于贯入[11]。

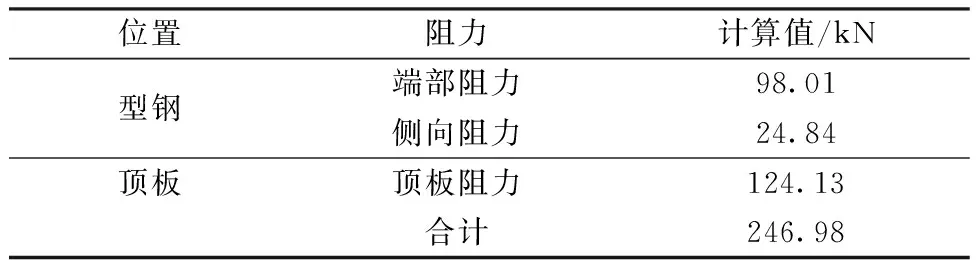
表1 重力基础贯入计算值

带有裙板的浅基础受到纯剪切状态时,受到裙板以上土壤的作用导致其侧向阻力增加,其抗侧滑能力有所增加,包括主动和被动土壤阻力。该浅基础的侧向阻力包括平板侧向抗滑移阻力以及型钢土壤阻力,其中平板侧向抗滑移阻力按照API RP 2GEO—2011中黏土的不排水水平抗滑移能力计算,见式(3):

Hd=suoA

(3)

式中:Hd——最大水平载荷;

suo——基础面的土壤剪切强度;

A——平板的面积。

不排水状态下的裙板极限水平剪切阻力计算见式(4):

ΔH=KrusuaveAh

(4)

式中:ΔH——极限水平阻力;

suave——海床表面至基础面的平均土壤剪切强度;

Ah——基础嵌入的垂直横截面积;

Kru——不排水水平土壤反力系数。

Kru与裙板的粗糙度、基础形状、侧面剪切、贯入深度以及由于安装、破裂或冲刷造成的土壤和基础之间的间隙等相关。当环境和土壤状况较好,主动和被动土压力均发生作用,Kru取值为4;而当由于安装扰动造成的主动土压力失效,但被动面无较大冲刷时,Kru取值为2。

分别采用不同的水平土壤反力系数计算得到的浅基础侧向稳定性的上限和下限见表2。由表2可见,与不带裙板的浅基础相比,通过设置型钢浅基础的侧向阻力值大幅度增加,上限值得到的侧向阻力增大了近5倍,下限值得到的侧向阻力增大近2.5倍,因而设置裙板可以大大提高黏土中浅基础的侧向稳定性。

表2 重力基础剪切性能计算值

2 有限元模型

浅基础的理论计算中包括众多假定,其中贯入计算采用桩的近似计算方法,也考虑了浅基础顶板承载力的影响;侧向稳定性计算根据不同反力系数得到了两组侧向阻力结果。为验证以上假定,根据有限元方法对该浅基础的贯入特征和侧向稳定性进行分析。采用通用有限元软件建立计算模型,包括浅基础和土壤,如图2所示,土壤模型的长和宽各为10倍的对应基础边长,总深度为10 m,其中初始下部土壤深度为8 m,上部空隙深度为2 m;贯入和侧向稳定性采用两个模型,可通过调整土壤和防沉板之间的相对位置来实现。

图2 有限元模型

采用耦合欧拉-拉格朗日方法(CEL)进行显式计算分析来模拟准静态过程,其中土壤采用欧拉材料,钢板材料采用拉格朗日材料;钢板和土壤之间的摩擦系数为0.5,土壤为实体单元,材料采用库伦材料模型,满足理想弹塑性条件,弹性模量为2.5 MPa,泊松比为0.49,粘聚力为3 MPa;钢板为壳单元,在几何中心参考点处建立刚体约束,输出参考点的反力。边界条件施加到土壤的侧面和底面上,其速度设置为0,认为无欧拉材料流入和流出。贯入分析时施加垂直向下的位移载荷为300 mm,计算时间取0.5 s;侧向稳定性分析时施加水平位移载荷为40 mm,计算时间取1 s。

3 计算结果及分析

经过有限元计算贯入分析得到的位移-反力曲线如图3和图4所示。由图3可见,计算在浅基础贯入0.02 m后趋于稳定,图4是0.02 m以后的位移-反力曲线与理论值的比较。由图4可见,在浅基础贯入0.02～0.30 m的深度内,反力在100～270 kN之间变化,大部分位于理论计算值247 kN以内,因此,理论计算和有限元分析的结果基本符合,可按照上述的理论计算估计该浅基础的贯入力,以安全系数为3.0考虑,则结构压载至少要达到750 kN。

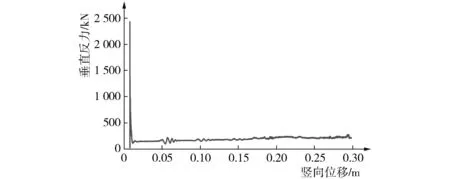
图3 贯入位移-反力曲线

图4 贯入计算理论与分析结果比较

经过有限元计算侧向稳定性分析得到的位移-反力曲线如图5和图6所示。由图5可知,有限元计算在水平位移达到0.07 m后逐步增大直到稳定,图6是0.07 m后的位移-反力曲线与理论上限和下限值的比较。由图6可见,浅基础的极限水平阻力在60 kN左右,与理论上限值符合,由于在有限元模型计算中认为土壤处于初始状态,未考虑贯入时的土壤扰动以及冲刷等环境条件,工程设计中的侧向阻力应在理论上限和下限值之间,以安全系数为2.0考虑,则结构的最大抗侧滑能力为17～30 kN。

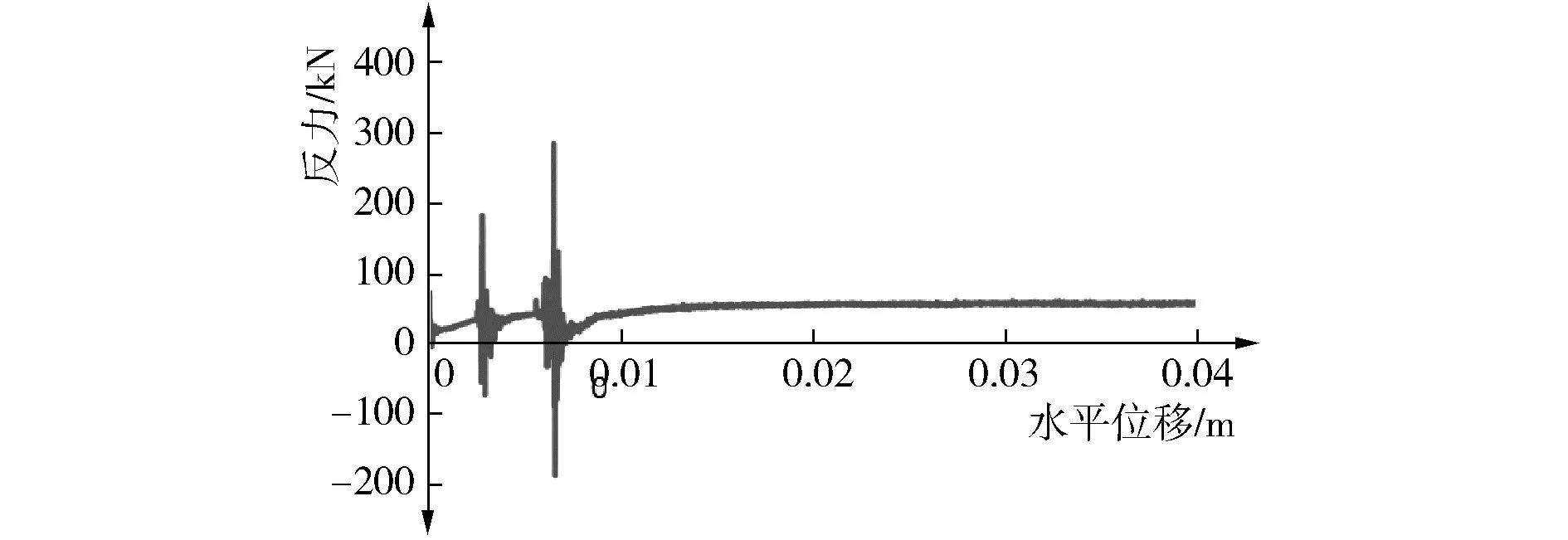
图5 侧向位移-反力曲线

图6 侧向稳定性计算理论与分析结果比较

4 结论

对于带有型钢作为裙板的水下设施浅基础,提出了采用理论公式和有限元模型进行基础计算和分析,验证了水下设施浅基础的贯入和侧向稳定性满足设计要求,得到结论如下:

4.1 水下设施浅基础贯入计算需要同时考虑裙板的贯入阻力和顶部的平板阻力,贯入阻力可近似采用桩基础的贯入公式计算,包括裙板的端部阻力和侧向摩擦阻力,平板阻力可近似采用浅基础的承载力公式计算。

4.2 通过设置裙板可以大幅度提高水下设施浅基础的侧向稳定性,当基础下的土壤未受到扰动和环境条件的影响,主动和被动土压力均起作用,可以得到侧向阻力的上限值,否则应根据现场条件在上限值和下限值之间选取。

4.3 采用基于耦合欧拉-拉格朗日(CEL)的显式有限元计算方法,可以得到准静态过程的水下设施浅基础贯入和侧向稳定性结果。