NiCoCrFeAlTiMoW 合金长期时效过程中γ′相粗化对拉伸性能的影响
刘继文,胡朝辉,王君阳,林雅婷,张 璐,2*
(1 沈阳航空航天大学 材料科学与工程学院,沈阳 110136;2 沈阳航空航天大学 航空制造工艺数字化国防重点学科实验室,沈阳 110136)
镍基高温合金主要应用在航空发动机、燃气轮机中的涡轮叶片等高温部件,在高温下仍能保持高强度、抗热腐蚀等优异性能,镍基高温合金的强度与γ′相密切相关。但在高温服役过程中,γ′相易粗化,其尺寸增加会显著降低合金的高温强度进而减少其使用寿命。例如,候介山等[1]对K44 镍基高温合金在800,850 ℃ 和900 ℃下进行长期时效处理,合金的强度随着γ′相平均尺寸的增大而降低。合金强化机制主要以沉淀强化中的强位错对切过机制为主,其强度贡献随着γ′相平均尺寸的增大而降低。因此对于抑制γ′相粗化、延长合金寿命具有重要意义。有研究表明:难熔元素的添加会显著降低γ′相的粗化速率[2-3]。马书伟等[2]通过研究三种不同Re 含量的单晶高温合金发现,在时效温度相同时,随着Re 含量的增多,γ′相粒子平均尺寸减小,粗化速率显著降低。这是由于Re可以降低γ′/γ 的错配度与界面能,从而使γ′相的粗化激活能提高,进而抑制γ′相粗化。师春伟等[3]通过改变DZ411 铸造高温合金中的Ta 含量发现,随着Ta 含量的增加,γ′相的粗化速率逐渐下降,Ta 是γ′相的形成元素,Ta 含量越高,γ′相的形成数量越多,但是由于Ta 元素的半径大,数量较多,将对基体中其他元素的扩散起到阻碍作用,从而使γ′相的尺寸减小,降低了γ′相的粗化速率。
综上可知,添加难熔元素可有效抑制γ′相粗化,但难熔元素会降低合金高温组织稳定性,长期服役过程中可能析出有害相(σ 相、μ 相和Laves 相),使合金力学性能恶化[4-7]。王博等[4]研究了W 含量对合金组织稳定性的影响,结果发现,W 的加入可显著抑制γ′相粗化,并且随着W 含量的增加,对γ′相的抑制效果更加显著,但在长期时效过程中均析出了σ 相和μ 相,且随着W 含量的增加,σ 相和μ 相的含量也相应增加。因此开发另一种有效抑制γ′相粗化的途径对于镍基高温合金极为关键。根据Ostwald 熟化机制,γ′相的长大主要是由Al,Ti 元素在基体中的扩散控制,因此通过降低Al,Ti 元素的扩散速率可以抑制γ′相的粗化[8]。高熵合金固溶体相具有典型的迟滞扩散效应,即原子在高熵合金中的扩散速率较低,从而降低γ′相的粗化速率。Tsai 等[9]探究了Co,Cr,Fe,Mn,Ni 在CoCrFeMnNi 高熵合金中的扩散过程,发现高熵合金中各元素的扩散激活能要显著大于其在传统Fe-Cr-Ni 三元合金中的扩散激活能。值得注意的是,Chen等[10]发现Al,Ti 元素在Al-Co-Cr-Fe-Ni-Ti 高熵合金中的扩散速率较低,且显著低于在Ni-Al-Cr,Ni-Al 和Ni-Al-Ti 等面心立方合金中的扩散速率。
基于以上分析,本工作设计了一种具有高熵固溶体基体的γ′相强化型NiCoCrFeAlTiMoW 合金,探究其γ′相高温粗化行为与力学性能的演变规律及机制,以期为新型Ni 基高温合金的研发提供一定的参考。
1 实验材料与方法
1.1 实验材料
实验选用高纯度(≥99.9%)Ni,Co,Cr,Al,Ti,Fe,Mo 和W 金属为原材料,合金的化学成分(原子分数/%)为Co 18.0,Cr 10.5,Fe 9.3,Al 9.7,Ti 4.5,Mo 1.0,W 0.5,余量为Ni,如表1 所示。利用电子分析天平进行称量,精确到0.01 g。采用真空电弧熔炼炉,在高纯度氩气条件下(纯度大于99.997%),制备了3 组合金铸锭,为确保成分均匀,反复熔炼4 次。随后在750,850,950 ℃下对合金进行200 h 长时间时效处理,热处理使用OTF-1500X 型管式炉,选取5,10,50,100,200 h 5 个时间节点对合金组织形貌进行观察,并测试其室温拉伸性能,所有试样取出后进行淬火。

表1 NiCoCrFeAlTiMoW 合金名义成分(原子分数/%)Table 1 Nominal compositions of the NiCoCrFeAlTiMoW alloy (atom fraction/%)
1.2 实验方法
采用D-max-rB 型X 射线衍射仪(XRD)对试样的晶体结构进行表征,扫描角度为20°~100°,扫描速率为10 (°)/min。使用Quanta 200FEG 型扫描电镜(SEM)和能谱仪(EDS)分析试样的微观结构与化学成分。SEM 试样尺寸为4 mm×4 mm×8 mm,将试样依次用400#~2000#砂纸进行打磨后,进行电解抛光,电解液成分为170 mL H3PO4+10 mL H2SO4+16 g CrO3,电压为3~4 V,电解时间为8~20 s。利用扫描电子显微镜进行显微组织观察以及成分分析,选取5个扫描电镜视场,利用Image-Pro 软件分析统计γ′相的平均尺寸与体积分数。室温拉伸实验在Instron5569万能材料试验机上进行,拉伸试样总长度26 mm,标距14 mm,标距处宽度2 mm,厚度1.2 mm。
2 实验结果与分析
2.1 铸态合金显微组织
图1 为NiCoCrFeAlTiMoW 合金的XRD 谱图以及γ′相的扫描电镜组织。从图1(a)中可以看出,合金铸态下相组成主要为面心立方(face-centered cubic,FCC)和γ′相双相结构。从图1(b)中可以发现,铸态下球形γ′相均匀分布在FCC 基体中,且含量较高,经测量,γ′相平均直径为36.5 nm,γ′相体积分数约为55%。
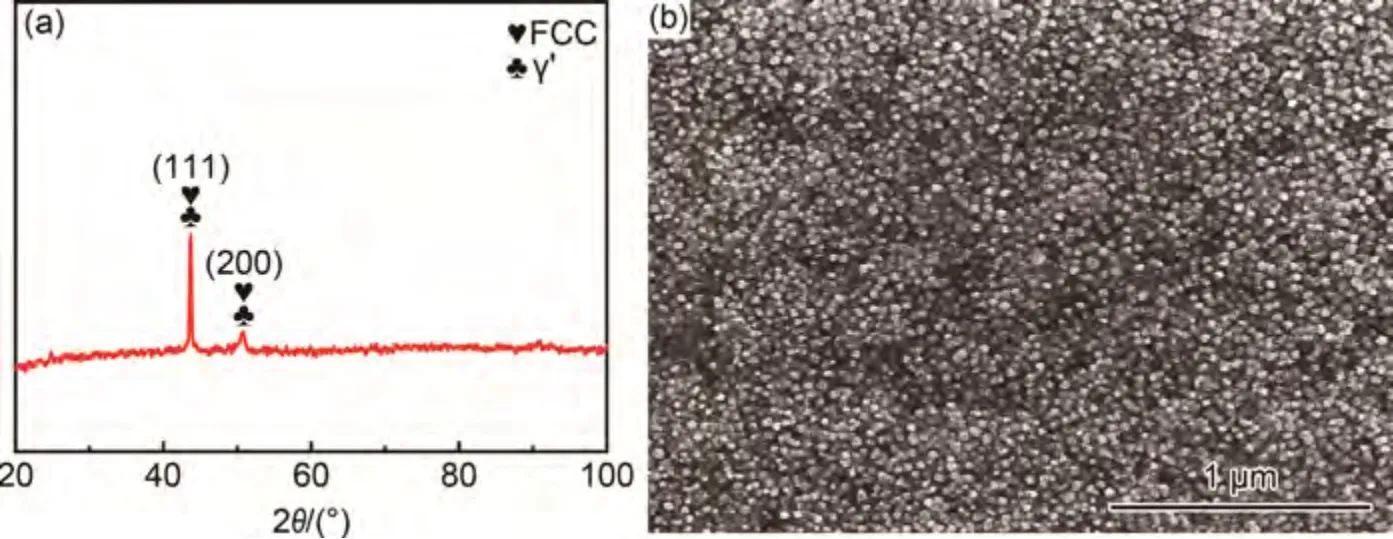
图1 合金的XRD 谱图(a)以及γ′相的形貌(b)Fig.1 XRD pattern of the alloy(a) and morphology of γ′ phase(b)
2.2 γ′相粗化规律研究
图2 为合金在750 ℃不同时效时间下的γ′相形貌。可以看出,在较低的时效温度下,γ′相尺寸并没有快速增长。当时效时间为5 h 时,γ′相尺寸几乎与铸态合金的γ′相尺寸相同;当时效时间为10 h 时,γ′相尺寸明显增大,所有的γ′相形状仍为球形,在基体上分布较为均匀,且γ′相之间尺寸差异较小。随着时效时间的延长,从50 h 开始,合金中的大部分γ′相仍然可以维持球形或类球形,此时可以发现,γ′相的尺寸出现了明显差异,尺寸较大的γ′相体积分数较高,有些γ′相已经开始逐渐变小,这表明大颗粒吞并小颗粒的Ostwald 熟化已经开始发生,主要是因为小颗粒曲率半径较大,化学势较高,导致其表面原子逐渐向基体中扩散,而大颗粒化学势较低,这些原子又重新沉积在大颗粒表面,使得大颗粒越来越大,小颗粒逐渐消失。与此同时,除了球形的γ′相外,还可以观察到一些不规则的条形γ′相,这些条状γ′相的形成主要是由于相邻的两个或几个γ′相在长大过程中相互连接而成,这可能是由于合金中γ′相含量较多,彼此距离较近,从而发生γ′相的凝并。图3 为合金在850 ℃下时效不同时间的γ′相形貌。当时效时间达到5 h后,γ′相尺寸已明显增大。时效200 h 后,γ′相的直径由最初的36. 5 nm 增大至160.6 nm。同时,从图3(a)中可以看到,当时效温度提升至850 ℃时,保温5 h 后就发生了γ′相凝并现象。图4 为合金在950 ℃下时效不同时间的γ′相形貌。可见,在整个过程中γ′相始终为球形,其尺寸和形状分布仍然比较均匀,并且γ′相尺寸增长较快。当时效时间为200 h 时,γ′相的平均直径达到了422.9 nm。表2 为不同温度时效过程中合金γ′相平均直径的变化规律。综上所述,随着时效温度的升高,γ′相粗化速率增大,且γ′相凝并时间缩短。

图3 合金在850 ℃下时效不同时间的γ′相形貌(a)5 h;(b)10 h;(c)50 h;(d)100 h;(e)200 hFig.3 γ′ phase morphologies of the alloy aged at 850 ℃ for different time(a)5 h;(b)10 h;(c)50 h;(d)100 h;(e)200 h

图4 合金在950 ℃下时效不同时间的γ′相形貌(a)5 h;(b)10 h;(c)50 h;(d)100 h;(e)200 hFig.4 γ′ phase morphologies of the alloy aged at 950 ℃ for different time(a)5 h;(b)10 h;(c)50 h;(d)100 h;(e)200 h

表2 时效过程中γ′相的平均直径变化Table 2 Average diameter change of γ´ phase during aging
表3 为合金在不同温度以及不同时效时间γ′相体积分数的变化情况。可以看出,当时效温度为750 ℃和850 ℃时,γ′相体积分数的数值上下浮动较大。而在950 ℃时效过程中,γ′相体积分数并没有出现非常明显的变化。结合表2 与表3 可知,γ′相已经在合金中达到了最大析出量,并已越过形核阶段,进入稳定的熟化阶段,且当时效温度较低时,γ′相体积分数的稳定度最低,随着时效温度的升高,γ′相体积分数的稳定度逐渐提升。
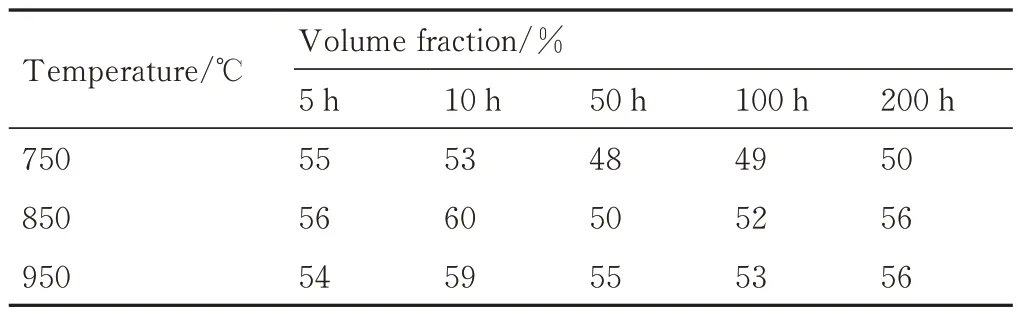
表3 时效过程中γ′相体积分数随温度变化情况Table 3 Variation of γ´ phase volume fraction with temperature during aging
2.3 γ′相粗化动力学
图5 为不同时效温度下的d3(t)-t关系。在3 个温度下,d3(t)与t均具有较好的线性关系,通过对散点进行拟合,并求出相应的直线斜率,可求得750 ℃下的粗化速率常数K750=1.33×10-28m3/s,850 ℃下粗化速率常数K850=6.09×10-27m3/s,950 ℃下粗化速率常数K950=1.08×10-25m3/s。
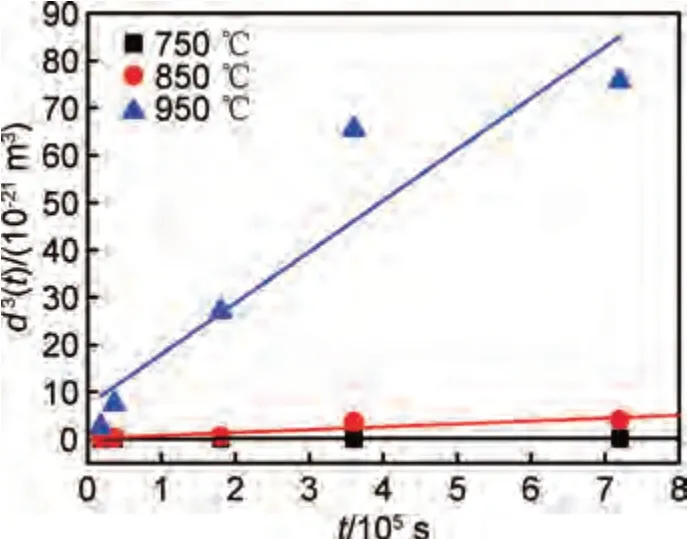
图5 不同时效温度下γ′相平均直径与时效时间的关系Fig.5 Average diameter of γ′ phase at different aging temperatures versus aging time
根据MLSW 理论,γ′相粗化过程中粗化速率K可以表示为[11]:
式中:γ为基体与γ′相界面处的比界面能;D为扩散系数;Ce为基体中溶质原子的浓度;Ω为γ′相的平均摩尔体积;ρm为约化半径的最大值;v为γ′相的粗化速率;R为气体常数;T为绝对温度。根据Arrhenius 方程,扩散系数D可以表示为:
式中:D0为扩散常数;Q为扩散激活能。将式(2)代入式(1)可得:
将两边同时取对数运算可得:
根据式(4),激活能Q可以从lnKT与1/T直线的斜率中求得,图6 为合金的lnKT与1/T直线关系图。通过计算图6 中的直线斜率,可知合金的扩散激活能Q=357 kJ/mol。相对而言,Ni 基高温合金的扩散激活能一般约为Al,Ti 原子在Ni 基固溶体中的扩散激活能,通常在257~290 kJ/mol 之间[11]。由此可见,Ni46.5Co18Cr10.5Fe9.3Al9.7Ti4.5Mo1W0.5合金具有较高的扩散激活能。γ′相粗化过程主要由Al,Ti 原子在基体中扩散控制[8],因此借助TEM-EDS 分析基体与γ′相的化学成分,如表4 所示。合金的熵值计算公式[12]为:
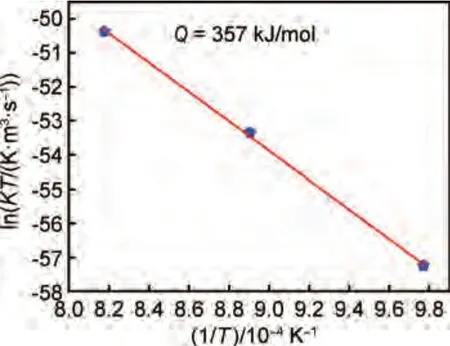
图6 合金的lnKT 与1/T 函数关系Fig.6 lnKT of alloy as a function of 1/T

表4 合金中基体以及γ′相的成分(原子分数/%)Table 4 Compositions of the matrix and γ´ phase in the alloy (atom fraction/%)
式中ci为第i种元素在高熵合金中的原子分数。
根据式(5)计算出了合金名义成分的熵值和合金基体成分的熵值,分别为1.56R和1.60R。由此可知,合金基体并非为Ni 基固溶体相,而是以NiCoCrFe 为基的高熵固溶体相,高熵相内部原子排列混乱,具有典型的迟滞扩散效应[13],使Al,Ti 原子在基体中的扩散变得更加困难,导致Ni46.5Co18Cr10.5Fe9.3Al9.7Ti4.5Mo1W0.5合金具有较高的扩散激活能。
2.4 合金的室温屈服强度随γ′相粗化的演变
随γ′相尺寸的增大,合金的力学性能也将发生改变,对750,850,950 ℃时效不同时间后的合金进行室温拉伸性能测试,结果如图7 所示。可以看出,在750 ℃时效时,合金的屈服强度随时效时间的延长逐渐增大,当时效时间为200 h 时屈服强度达到最大值,此时屈服强度为888 MPa。在850 ℃时效时,合金的屈服强度随时效时间的延长先升高后降低。在950 ℃时效时,合金的屈服强度随时效时间的延长而逐渐降低,但在时效时间为5 h 时,屈服强度降低不明显,当时效时间延长至10 h 后,屈服强度急剧下降,随后下降变得缓慢,850 ℃时效后的强度始终高于950 ℃时效后的强度。
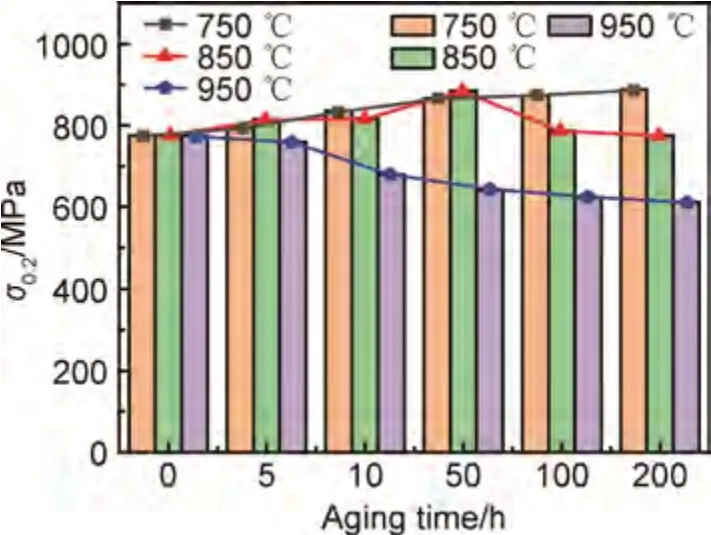
图7 不同温度时效不同时间后合金的室温拉伸性能Fig.7 Room temperature tensile properties of the alloy after aging at different temperatures for different time
对于铸态沉淀强化型合金而言,其屈服强度主要来源于固溶强化与沉淀强化,因此,合金屈服强度可粗估为二者之和。从固溶强化的角度分析,由于Ni,Co,Cr,Fe 四种元素的原子半径接近,均在0.124~0.127 nm 范围内,引起的晶格畸变非常小。而Al,Ti,Mo,W 四种元素的原子半径分别为0.143,0.146,0.139,0.137 nm,因此,基体中的固溶强化主要源于Al,Ti,Mo,W。依据上述分析,可将基体近似看作Ni-Al-Ti-Mo-W 固溶体,来估算固溶强化对屈服强度的贡献。根据Feltham[14]提出的Ni 基高温合金固溶强化模型,各元素固溶强化值可以表示为:
式中:ki为第i种元素的强化系数;Ci为第i种元素在基体中所占的原子分数。在多元体系中,固溶强化对屈服强度的贡献表达式如下[15]:
本实验中,p取1/2[15],将Al,Ti,Mo,W 视为溶质原子,相应的kAl,kTi,kMo,kW值[16]分别为225 MPa/(原子分数/%)1/2,775 MPa/(原子分数/%)1/2,1015 MPa/(原子分数/%)1/2和977 MPa/(原子分数/%)1/2,表5 为合金基体相与γ′相的晶格常数以及错配度,Ci值可从表5 中获得。经计算,固溶强化对屈服强度的贡献值为153 MPa。

表5 合金中晶格常数以及错配度变化Table 5 Changes in lattice constants and mismatch in alloys
从沉淀强化的角度分析,当合金中的γ′相尺寸较小时,位错以弱位错对形式切过γ′相,但当γ′相尺寸增大至一定值后,强位错对切割γ′相将成为主要机制。强弱位错对切割模型的屈服强度表达式如下[17]:
式中:G为合金的剪切模量;f为γ´相的体积分数;b为柏氏矢量;d为γ´相的平均直径;γAPB为反相畴界能;w和M为常数。
上述参数中,w与位错之间的弹性张力有关,本实验取2.8[17]。G,γAPB可以通过JMatPro 软件获得,其中G=81.9 GPa,γAPB=0.173 J/m2(Ni65.87(Al15.54Ti18.59))[18],M为常数,对于FCC 合金,通常取为3.06[19]。当合金在850 ℃以及950 ℃时效时,熟化已经进入稳定阶段,γ′相只发生尺寸上的变化而其体积分数保持基本不变,所以本实验将铸态γ′相体积分数f取为55%。柏氏矢量b在FCC 合金中与基体晶格常数aγ的关系如式(10)所示[20]:
图8 为合金(311)衍射峰的分峰结果。经计算,基体的晶格常数aγ=0.3592 nm,γ′相的晶格常数aγ′=0.3586 nm,根据式(10)可得该合金的柏氏矢量为0.2540 nm。

图8 合金(311)分峰结果Fig.8 (311) peak splitting results of alloys
在850 ℃以及950 ℃下时效时,熟化已经进入稳定阶段,基体中溶质原子分数已经达到动态平衡,所以时效过程中产生的固溶强化数值可认为不变。因此,在切过机制的基础上,本实验将固溶强化对合金屈服强度的贡献设定为一定值,取为153 MPa。所以,不同切过机制主导的合金屈服强度的表达式如下:
根据以上参数计算了不同机制下的屈服强度随γ′相直径d的变化情况,如图9 所示。可以看出,弱位错对切过机制的屈服强度随着d的增大而增大,而强位错对切过机制的屈服强度随着d的增大而降低,并且二者发生转变的临界直径dc约为90 nm,此时的屈服强度具有最大值。在750 ℃时效处理时,γ′相最大尺寸为56.9 nm,未超过临界直径dc,其屈服强度随着γ′相尺寸增加而增大。在850 ℃时效处理时,屈服强度随着γ′相尺寸增加先增大后减小,在50 h 时效后屈服强度达到最大值,此时γ′相直径约为86 nm,而时效时间为100 h 时,γ′相直径为155.4 nm,超过临界直径dc,屈服强度随着γ′相尺寸增大逐渐降低。在950 ℃时效5 h 后,γ′相直径已经达到136 nm,超过临界直径dc,屈服强度随着γ′相尺寸增大逐渐减小。值得注意的是,图7 中实际屈服强度与模型中预测的屈服强度存在差异,这是由于模型相关参数,例如剪切模量G,反向畴界能γAPB是通过调研相似成分合金的估算值,与本实验合金的实际数值存在差异。但是合金室温屈服强度随γ′相尺寸的变化规律符合强弱位错对转变机制模型的预测结果。因此可以确定合金的主要强化机制为沉淀强化与固溶强化,且切过机制为合金的主要强化机制。

图9 不同切过机制屈服强度与γ′相平均直径之间的关系Fig.9 Relationship between the yield strength of different cutting mechanisms and the average diameter of the γ′ phase
3 结论
(1)在不同温度时效200 h 过程中,γ′相始终为球形,γ′相平均尺寸逐渐增加,在粗化的同时发生相邻γ′相凝并的现象,且时效温度越高凝并发生的时间越早。
(2)γ′相在750,850,950 ℃下的粗化速率分别为1.33×10-28,6.09×10-27,1.08×10-25m3/s,扩散激活能Q=357 kJ/mol。合金具有较高扩散激活能的原因主要是基体为成分复杂的高熵固溶体,使Al,Ti 原子在基体中的扩散变得更加困难。
(3)经750 ℃时效后的合金屈服强度逐渐升高,这主要是由于γ′相直径的最大值未超过临界转变直径,其沉淀强化机制为弱位错对切过机制,屈服强度随γ′相平均直径增大而增大。经850 ℃时效后的合金屈服强度先升高后降低,这主要与γ′相尺寸的增加有关,随着γ′相平均直径的增加,位错切过机制由弱位错对切过机制转变为强位错对切过机制,其临界转变直径约为90 nm。950 ℃时效后的合金屈服强度逐渐降低,这是由于合金中的γ′相尺寸在时效初期就已经超过临界直径,其沉淀强化机制为强位错对切过机制,强度随γ′相尺寸增大而降低。

