重力坝地震断裂的多边形比例边界有限元模型研究

蒋新新，钟 红，李云途，牛景太，邓志平，黄红元

(1.南昌工程学院，江西 南昌 330099；2.流域水循环模拟与调控国家重点实验室，中国水利水电科学研究院，北京 100038)

1 研究背景

我国是一个地震多发国家，西部地区建设的多座高坝工程面临严峻的抗震问题，对此工程界和学术界予以高度关注[1-2]。按照现行抗震规范的规定，对抗震设防类别为甲类的重力坝，除按设计地震进行抗震设计外，通常还应论证其在最大可信地震下的灾变安全裕度，允许出现一定程度的损伤开裂，但须避免发生溃坝导致库水失控下泄[3-4]。在强震作用下重力坝产生严重震损的实例不多，其中以印度Koyna重力坝最为典型。该坝在1967年Koyna地震中非溢流坝段出现贯穿性裂缝，促使学术界对重力坝地震开裂破坏机理开展深入研究[5]。Chopra等[6]对Koyna大坝线弹性地震响应的分析表明坝体上部出现了较大拉应力，根据拉应力分布预测的坝体开裂区域与观测结果基本吻合；Batta等[7]应用线弹性断裂力学和边界元分别模拟了单条和多条预设裂缝情况下的Koyna大坝裂缝扩展过程，发现在坝体上下游面预设的裂缝均可能扩展形成贯通裂缝；Zhang等[8]采用弥散裂缝模型和扩展有限元法分析了裂缝扩展对大坝地震响应的影响，结果表明下游折坡处最先开裂并向上游坝面扩展直至形成贯穿裂缝。地震作用下大坝裂缝扩展会影响坝体的整体性，降低其整体刚度，在地震往复作用下出现裂缝的快速发展导致大坝失效破坏[9-10]。因此，为准确评估大坝在强地震作用下的响应，发展混凝土坝动态开裂扩展数值模型很有必要，其中，描述混凝土开裂引起的非连续位移场和预测裂缝扩展路径是关键问题。

混凝土坝的断裂力学模型主要有分离式裂缝模型[11]和弥散裂缝模型[12]。分离式裂缝模型通过在裂缝扩展过程中引入新的节点描述裂缝轨迹，能够直观体现裂缝的扩展过程，且可以方便地考虑缝内水压力的影响。这种裂缝扩展模拟方式在有限差分法和有限元方法中应用较多，但是由于必须通过网格重剖分反映裂缝的扩展过程，导致前处理和计算工作量较大。为了提升分析效率，局部网格重剖分是有效的解决办法[13]。弥散裂缝模型通过降低开裂单元的刚度间接体现裂缝的影响，其优势是裂缝扩展过程中网格不需重剖分，代表性方法为扩展有限元法。目前扩展有限元法已经集成于ABAQUS软件平台，借助于ABAQUS强大的前后处理实现了多种类型的裂缝扩展模拟。但不能忽视的是，集成过程中简化了扩展有限元法裂缝尖端增强功能，且裂缝尖端需要位于单元边界上，可能导致计算不准确和收敛性问题[14]，从而影响裂缝扩展模拟的精度。

比例边界有限元法(SBFEM)[15]作为一种半解析的数值分析方法，兼具有限元法和边界元法的优势，具有降低一维和径向解析求解的特点[16-17]。近年来SBFEM在断裂分析中展现了明显的优势[18]，大为简化裂缝尖端奇异应力场的描述，且广义应力强度因子直接从单元应力模态中提取、适用于均质材料和界面材料等多种情况[19]。此外，多边形单元具有灵活地分割重组网格的优势，相应发展的局部网格重剖分技术能够高效地描述裂缝的扩展过程。施明光等[20]、钟红等[21]基于SBFEM和多边形网格局部重剖分技术分析了重力坝在静水超载作用下的断裂过程；Li 等[22]建立了重力坝水力劈裂的SBFEM模型，着重研究了裂缝张合过程中缝内水压力的变化及对大坝断裂的影响。本文在此基础上将多边形比例边界有限元法应用于重力坝地震断裂分析，推导了相应的动力控制方程；提出了广义动态应力强度因子时域计算方法，考虑裂缝面动态接触条件，建立了一种全自动的重力坝分离式裂缝动态扩展模型；模拟了Koyna重力坝的地震断裂过程，并对模型网格密度和裂缝扩展步长等参数进行了敏感性分析。

2 多边形比例边界有限元原理与动力方程

2.1 多边形比例边界有限单元基本原理比例边界有限元法是一种在域边界离散而域内径向解析的数值分析方法。采用该方法的基本要求是满足相似条件，即站在相似中心位置，域边界的所有点均直接可见。若采用多边形对求解域进行离散，每个多边形采用比例边界有限元法求解[23]，则为多边形比例边界有限元法。如图1(a)所示，建立含预设裂缝的重力坝多边形比例边界有限元模型，多边形单元可以方便地适应模型复杂边界，预设裂缝由多边形裂缝比例边界有限单元描述。如图1(b)所示，裂缝单元相似中心“SC”位于裂缝尖端，整个单元由边界向相似中心等比例缩放形成，其中裂缝面由裂缝开口节点向相似中心缩放来描述，无须特殊处理。多边形比例边界单元径向坐标记为ξ，在相似中心ξ=0，在单元边界处ξ=1，取值范围为[0，1]；边界采用两节点线性单元离散，线性单元节点逆时针排列，环向坐标记为η，取值范围为[-1，1]。

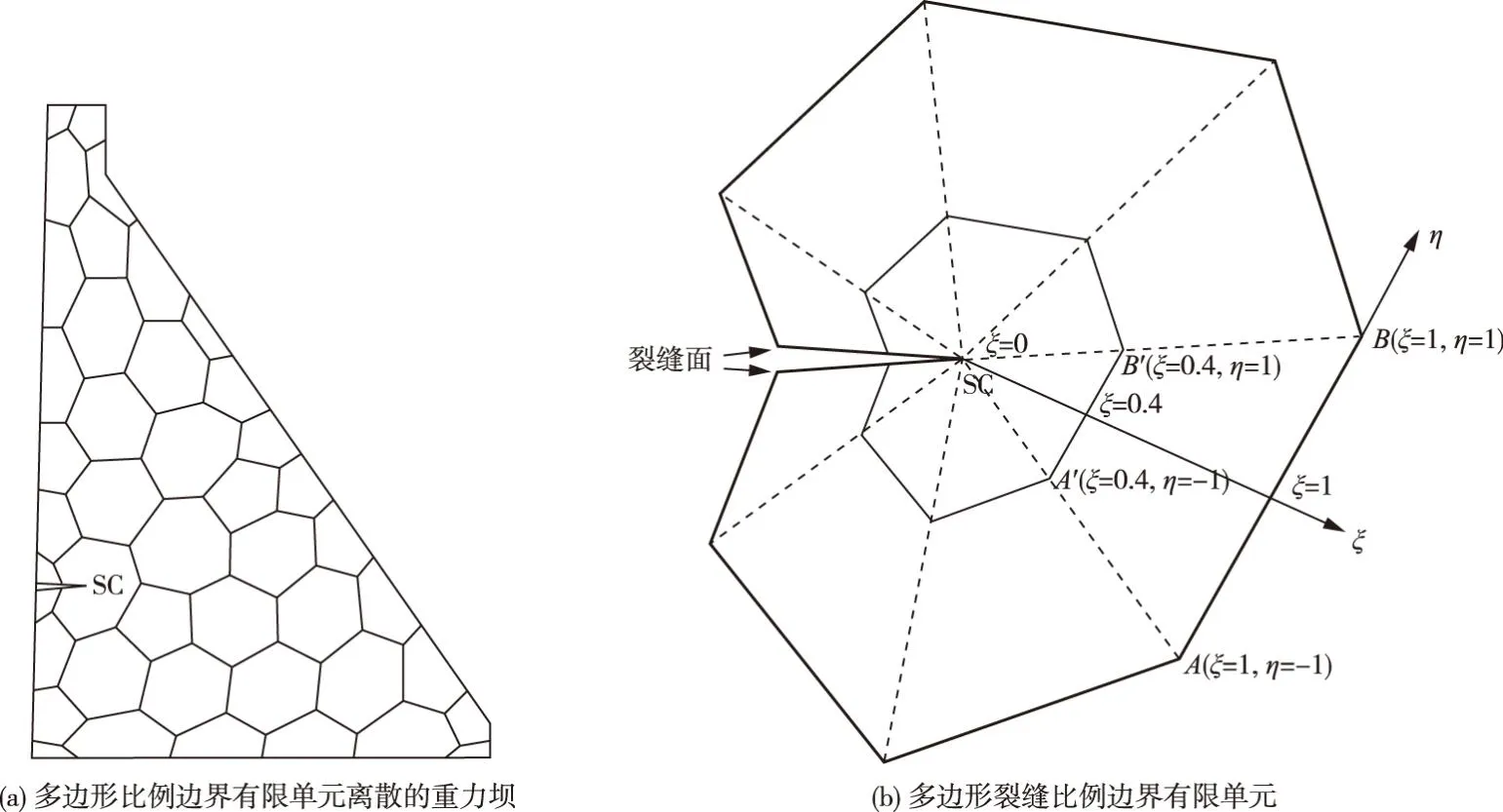
图1 重力坝多边形比例边界有限元模型示意

在不计体力和裂缝面荷载情况下，由虚功原理可导出多边形比例边界有限元控制方程[15，19]为：

(1)

式中：{u(ξ)}为节点位移函数；{q(ξ)}为节点力函数；[Z]为Hamilton矩阵[19]。

采用特征值分解或者Schur分解[18]均可求解控制方程(1)。以特征值分解为例，多边形内任一点的位移{u(ξ，η)}可表示为节点位移函数{u(ξ)}沿环向边界的插值，具体表达式为：

(2)

由位移导出对应多边形内任一点的应变和应力，其表达式为：

(3)

(4)

2.2 刚度矩阵和质量矩阵对于任意的多边形比例边界有限单元，单元刚度矩阵[Ke]表达式为：

(5)

多边形比例边界有限单元质量矩阵由边界上线性单元根据单元节点连接组装得到，其表达式为：

(6)

式中[m]为系数矩阵的缩略表达式，其仅取决于多边形单元的密度和单元形状[15]。

2.3 多边形比例边界有限元静动力方程对于由多边形单元离散的任意结构体系，结构整体刚度阵[K]和整体质量阵[M]类似于有限元法通过单元组装形成，因此静力平衡方程和动力方程分别为：

[K]{d}={F}

(7)

(8)

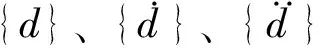
实际工程动力分析需要考虑阻尼的影响，采用瑞利阻尼，阻尼矩阵通过结构整体刚度阵和质量阵的线性组合得到，其表达式为：

[C]=α0[M]+α1[K]

(9)

式中α0、α1为组合系数，均与结构的频率和材料阻尼相关。

采用Newmark方法求解式(8)可获得任意时刻结构的位移场、速度场和加速度场，应变场和应力场可分别由式(3)(4)通过位移场导出。

从总的流程来说，对于采用多边形比例边界有限单元离散的结构动态断裂模拟，类似于有限元法，每一时间步先进行结构动力分析，在此基础上求解结构断裂参数并进行动态断裂分析。

3 广义动态应力强度因子及裂缝扩展准则

3.1 广义裂缝动态应力强度因子对于无限平面内以速度为v扩展传播的稳态裂缝，其动态应力强度因子[24]计算公式为：

(10)

式中：应力强度因子K上标“eq”表示依据瞬时应力场计算的瞬态应力强度因子，上标“dyna”代表动态应力强度因子；kⅠ(v)、kⅡ(v)与裂缝传播速度和材料特性相关，其表达式为：

(11)

式中cd、cs和cR分别为压缩波、剪切波和瑞利波的波速。

3.2 多边形裂缝单元广义动态应力强度因子求解在SBFEM中，Song等[19]提出了广义应力强度因子以描述裂缝尖端应力奇异性，对均质材料断裂、界面断裂和V型缺口等断裂类型均适用。本文将其推广至结构的动态断裂分析，建立多边形裂缝单元的广义动态应力强度因子求解方法。

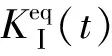
(12)

图2 由SBFEM模拟的多边形裂缝单元示意

引入裂缝特征长度L，根据关系式ξ=r/L推导瞬态广义应力强度因子为：

(13)

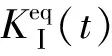
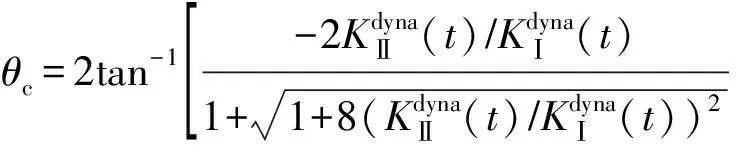
(14)

将裂缝扩展角θc代入下式，计算t时刻对应裂缝扩展角的等效应力强度因子K(t)：

(15)

当等效应力强度因子达到材料的断裂韧度，认为裂缝处于临界状态，即将扩展。在混凝土大坝断裂分析中裂缝扩展长度取为固定值Δa，每次扩展调用局部网格重剖分方法以形成新的裂缝边界，当裂尖触及模型边界或者动力分析完成均会触发断裂分析结束。

4 裂缝动态扩展模拟过程

4.1 多边形单元生成将结构自由剖分为三角形背景网格，进而转化为多边形单元。如图3(a)所示，对重力坝模型自由剖分得到三角形背景网格。如图3(b)所示，在模型内部，以三角形网格顶点为相似中心，将周围所有三角形的形心逆时针依次相连形成多边形；对于模型边界上的三角形顶点，将周围的三角形形心及边界线中点相连构造多边形，新生成多边形的形心作为相似中心；在裂尖点生成的多边形裂缝单元，取裂尖点坐标作为裂缝单元相似中心。最终形成含预设裂缝的重力坝多边形比例边界有限元模型如图3(c)所示。

图3 三角形网格转化为多边形网格示意

4.2 裂缝扩展局部网格重剖分裂缝扩展局部网格重剖分方法是对裂尖点附近局部网格区域进行重剖分，每一步扩展过程所需前处理工作量很小，只需更新重剖分区域内的节点及其位移、速度和加速度，从而有效地提高断裂分析效率。具体的网格重剖分过程如下：

(1)图4(a)为裂尖点附近三角形背景网格(黑线)和生成的多边形网格(蓝线)，C1为扩展前的裂尖点，由式(14)(15)根据裂缝应力强度因子计算裂缝扩展方向，再由所设定的裂纹扩展步长Δa得到新的裂尖点C2，依据裂缝扩展轨迹C1C2(红线)确定所切割的三角形背景网格(紫线包围区域)；

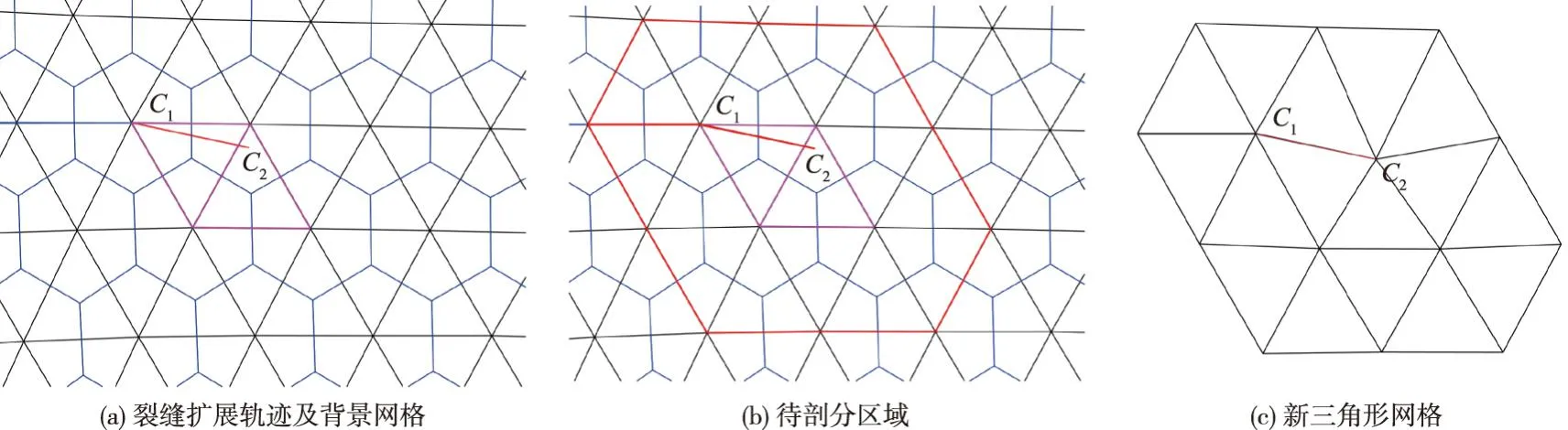
图4 多边形网格局部重剖分过程

(2)找出与被切割三角形相连的周边三角形网格，连接这些三角形的外边界，所围成的区域即为需要重新剖分的区域(图4(b)中的红线包围区域)；

(3)对图4(b)中的红线包围区域重新剖分三角形网格，其中新生成的裂缝面成为新的三角形网格边界的一部分，如图4(c)所示。将重剖分的三角形网格和图4(b)中的红线区域外原有三角形网格组合形成新的三角形背景网格，之后再按照4.1节给出的三角形转化为多边形网格过程生成新的多边形网格。

4.3 裂缝动态接触模拟算法大坝在地震往复作用下，若不对裂缝面施加任何约束条件，可能出现裂缝面相互嵌入的现象，即裂缝面法向相对位移出现负值。如图5所示，通过在裂缝面节点对之间施加接触弹簧以阻止裂缝面的嵌入，其基本思想类似于罚函数法，即将接触约束条件当作惩罚项加到系统的总泛函中，再对总泛函求极小。动态断裂分析时，一旦判断裂缝面相互嵌入，在动力平衡方程中加入接触弹簧刚度矩阵，不断调整其刚度迭代求解方程，直至满足裂缝面接触条件。接触弹簧刚度矩阵表达式为：

(16)

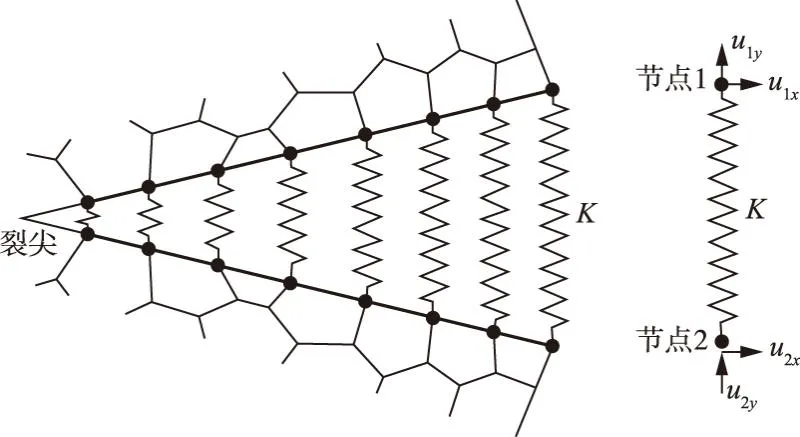
图5 裂缝面节点对施加接触弹簧示意

5 数值算例

Koyna重力坝地震破坏过程是大坝地震分析中的经典研究对象，本文模拟了该坝在地震作用下的断裂过程。已有研究表明裂缝最容易从下游折坡处起裂扩展形成上下游贯穿裂缝[7-8]，故在基于断裂力学的模拟中通常在下游折坡处预设裂缝。为与文献[8]结果进行对比，大坝的几何尺寸、材料参数、约束条件和荷载等均与之相同。大坝断面如图6所示，在坝体下游面高程66.5 m处(折坡点)预设水平裂缝，长度为1 m。坝体混凝土材料参数为：E=31 GPa，泊松比ν=0.2，密度ρ=2643 kg/m3。动力分析中坝体混凝土动态弹性模量取为35.7 GPa[27]，阻尼比取为5%，动力分析步长取为0.02 s，混凝土动态断裂韧度KⅠd=1.8 MN/m3/2。计算中采用平面应变假定。

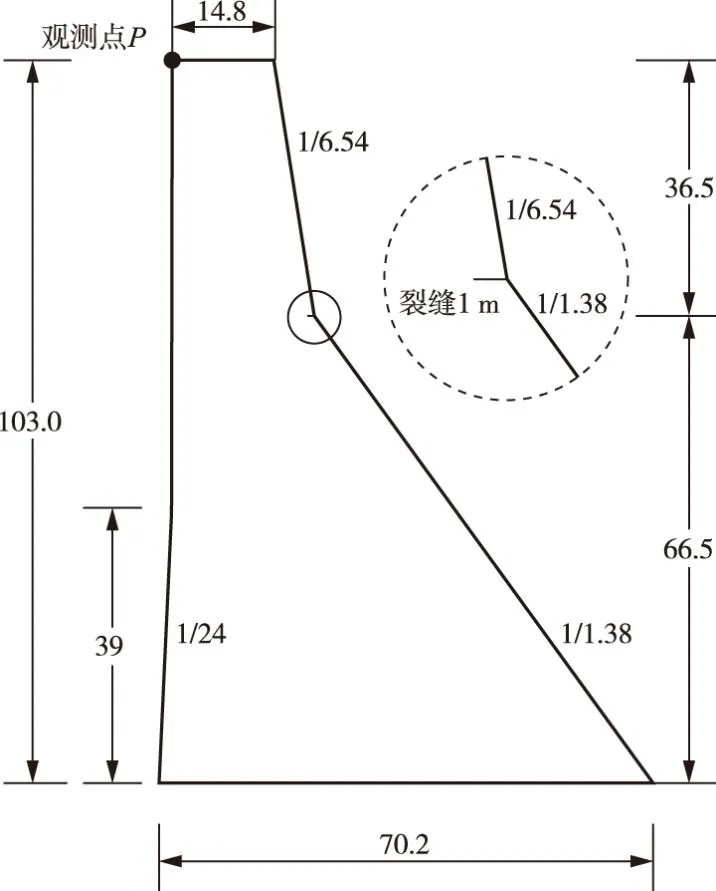
图6 预设裂缝的Koyna重力坝典型剖面图(单位：m)

上游水位取为96.5 m。水平向、竖向加速度幅值分别为0.49g和0.34g，图7为地震动加速度时程。采用Westergaard附加质量模型考虑动水压力，不考虑坝体-地基动力相互作用的影响。为阻止地震作用过程中裂缝面的嵌入，在裂缝面施加接触弹簧。

图7 Koyna地震波加速度时程

5.1 静力计算结果静力分析为后续动力分析提供初始状态。静荷载包括坝体自重和上游静水压力，分别采用图8所示的粗网格和细网格方案计算大坝响应，两种网格方案(图中G为坝体自重，左边箭头表示水压力)分别包含190个和475个单元，以及439个和1043个节点。图9为大坝变形图，其中图9(a)(b)均对应设置缝面接触弹簧的结果，图9(c)未设置缝面接触弹簧。本文以水平位移向下游为正，竖向位移向上为正。对应图9中三种情况计算的坝顶上游侧(点P)水平向位移分别为5.753、5.740和5.859 mm，竖向位移分别为-1.550、-1.553和-1.532 mm。可以看出，是否设置缝面接触弹簧对坝顶位移的影响较大，而对于设置缝面接触弹簧的情况，粗网格和细网格的计算结果接近，说明网格密度对坝顶位移影响不大。由于在静力作用下大坝下游预设裂缝处于受压状态，变形图也显示未施加接触弹簧的裂缝上下面发生了嵌入，而施加接触弹簧的裂缝面处于压紧状态，说明考虑裂缝面的接触条件是必要的。

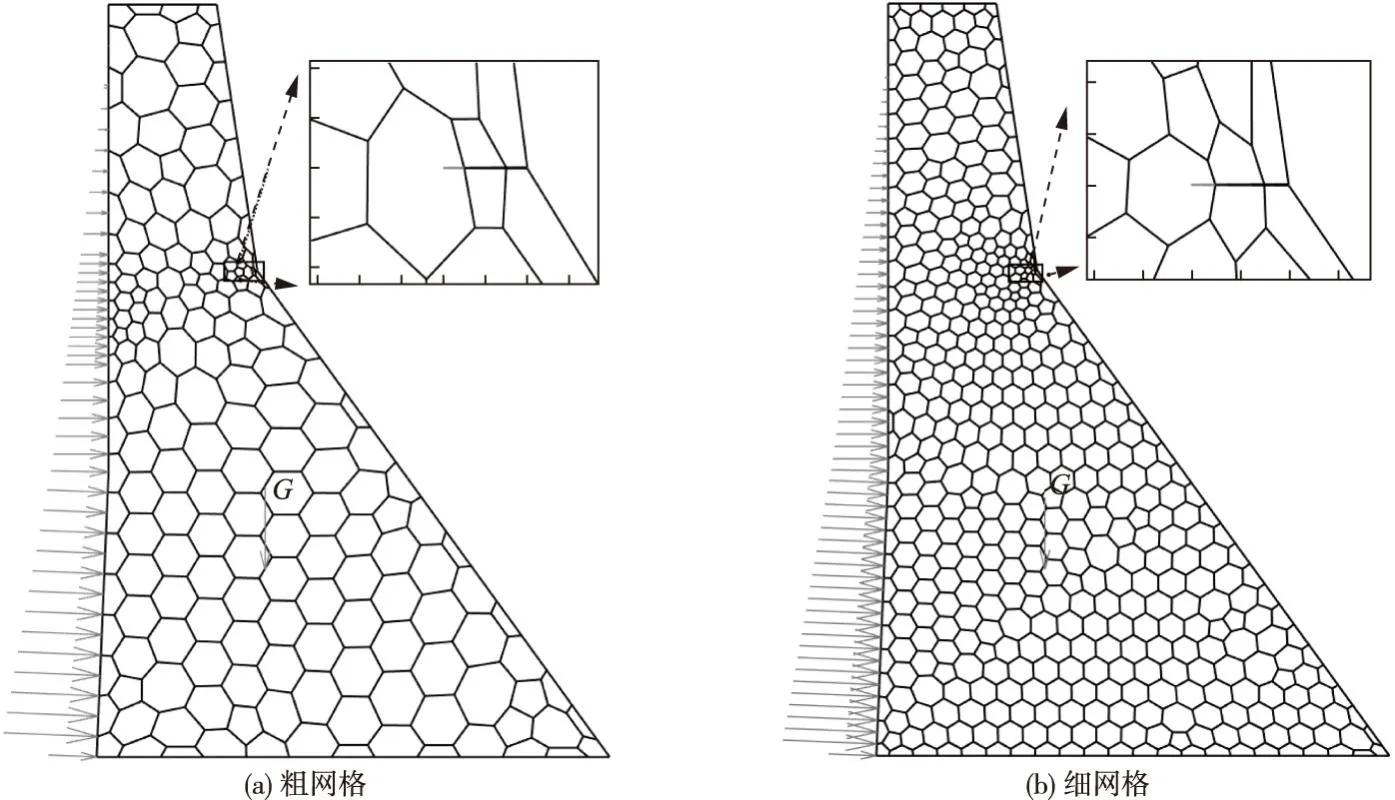
图8 SBFEM静力计算模型

图9 重力坝静力作用变形图(变形放大倍数：600)

5.2 地震断裂分析结果仍采用图8中粗网格和细网格模型模拟Koyna重力坝地震断裂过程。地震工况考虑自重+静水压力+地震荷载+动水压力，并研究网格密度和裂缝扩展步长对大坝地震响应和裂缝扩展过程的影响。

5.2.1 网格密度对计算结果影响 图10为采用SBFEM粗网格和细网格模型进行非线性断裂分析得到的坝顶观测点P的位移时程，并与不考虑裂缝扩展的线弹性分析结果进行对比，由结果可见：前2.06 s，三个模型计算的坝顶水平和竖向位移基本吻合，表明裂缝尚未扩展，大坝处于线弹性状态；2.06 s时刻预设裂缝起裂，粗、细网格模型计算得到的坝顶最大水平向位移分别为-10.06和-10.16 cm，较线弹性分析结果明显增大，反映出坝体刚度随裂缝扩展而降低。对比两种网格计算的位移结果可知，坝顶水平和竖向位移时程相似度极高，且峰值发生的时刻一致，说明SBFEM粗网格即可得到满意的计算结果。

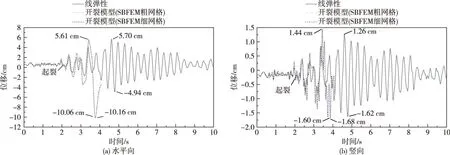
图10 不同模型计算的坝顶观测点P的位移时程

图11绘制了粗网格和细网格情况下模拟的坝体裂缝扩展轨迹，可看出本文模拟结果与文献[8]结果及振动台实验结果[26]吻合，验证了本文模型的正确性。同时，两种网格模拟的裂缝扩展轨迹非常接近，综合图10中坝顶位移响应结果，说明模型网格密度对动态断裂分析结果影响很小，粗网格在动力分析中具有足够的计算精度。图12和图13分别绘制了坝体裂缝扩展过程中不同时刻的变形图和位移云图，可以看出，预设裂缝起裂后以斜向下的角度迅速向上游扩展，在此过程中观测到地震的往复作用导致裂缝出现张开和闭合的现象。

图11 不同网格模型的裂缝扩展路径对比

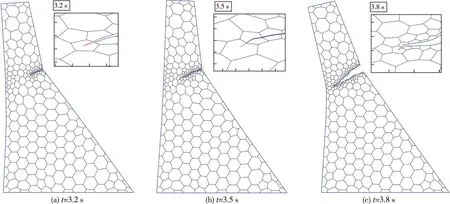
图12 Koyna重力坝粗网格模型不同时刻变形图(变形放大倍数：200)

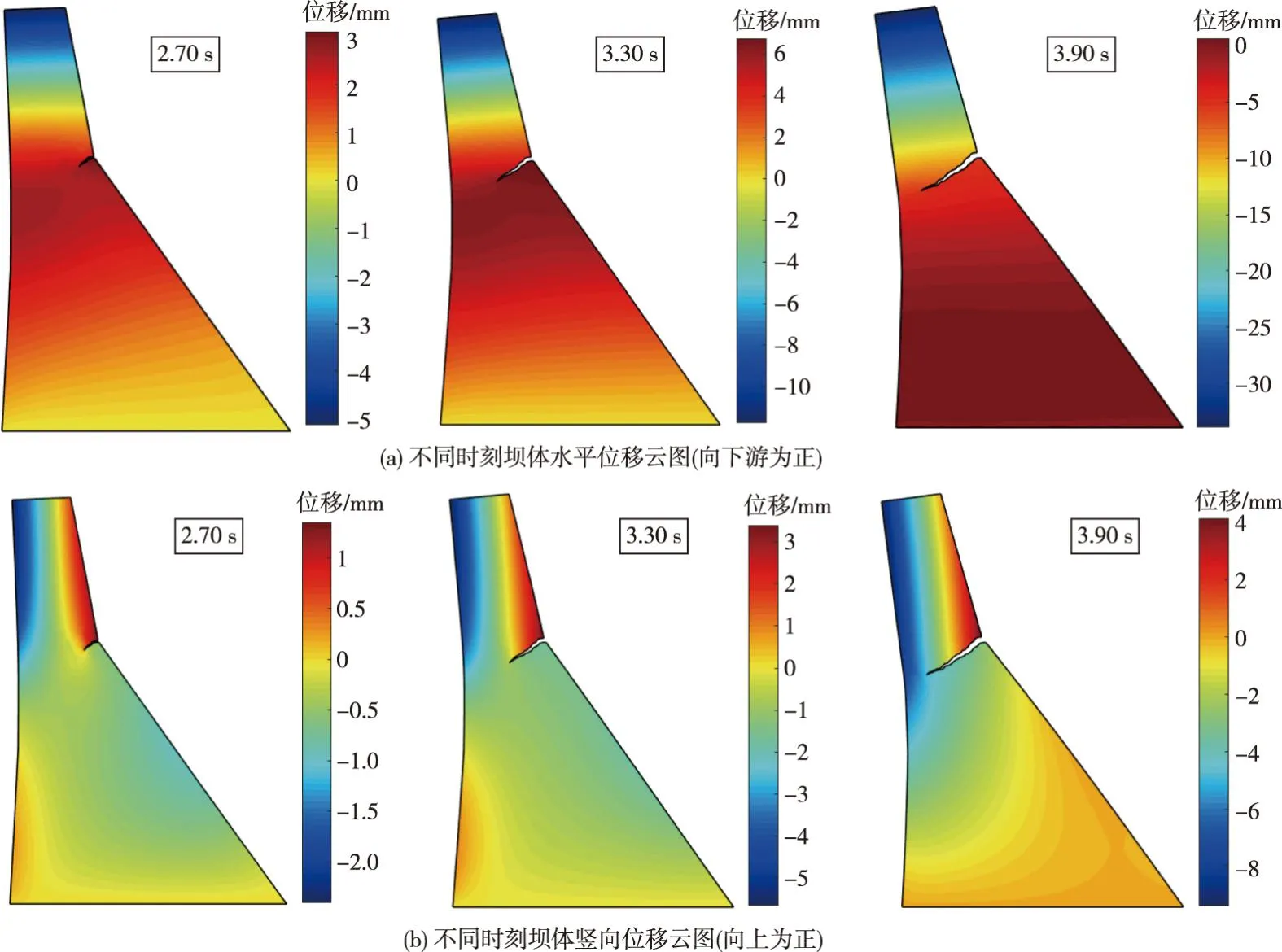
图13 Koyna重力坝粗网格模型不同时刻位移云图(变形放大倍数：200)

5.2.2 裂缝扩展步长对计算结果的影响 实际混凝土起裂后裂缝扩展步长受多种因素影响，如加载条件和骨料级配等，因而有必要探究模型中裂缝扩展步长的取值对于断裂模拟的影响。本次断裂分析以粗网格模型为例，

分别取0.4、0.8和1.2 m等三种不同的裂缝扩展步长，模拟Koyna重力坝的地震断裂过程。图14绘制了三种裂缝向上游坝面扩展形成贯通裂缝前的变形图，图15将不同裂缝扩展步长计算的最终裂缝扩展轨迹与文献[8，26]结果进行了对比。结果表明，三种裂缝扩展步长条件下模拟的大坝裂缝扩展轨迹接近；从裂缝扩展路径来看，步长取值越小会使得裂缝周边网格更密，裂缝扩展轨迹更为精细。

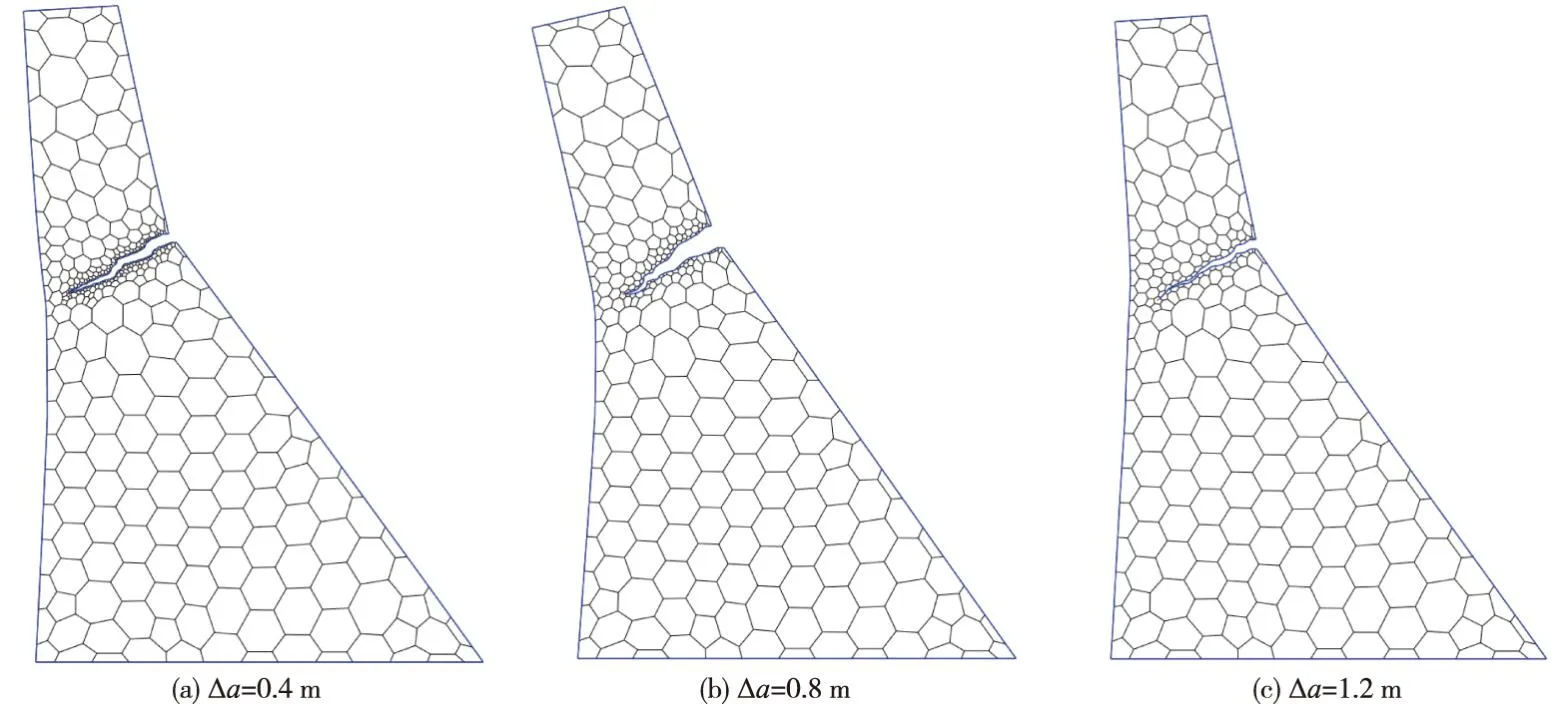
图14 不同裂缝扩展步长情况坝体变形图(变形放大倍数：200)

图15 不同裂缝扩展步长模拟的Koyna大坝裂缝扩展轨迹

图16为采用三种裂缝扩展步长计算的坝顶观测点P的水平和竖向位移时程，可看出裂缝扩展之前三种情况的坝顶位移时程吻合，裂缝扩展后随着步长的增大，裂缝张合次数减少，裂缝向上游扩展贯穿坝体用时越短，对应0.4、0.8和1.2 m扩展步长取值情况下形成贯穿裂缝用时分别为4.08、3.36和2.82 s。从图中也可看出，坝顶水平位移峰值随着裂缝扩展步长的增大而减小，说明裂缝扩展步长的取值会影响坝体的地震响应分析结果。进一步对比裂缝张开-闭合一个周期内(如2.3～2.8 s)的位移响应，坝顶水平、竖直位移峰值分别为-3.29和-1.25 cm，均来自裂缝扩展步长为1.2 m的情况。这是由于扩展步长取值越大，坝体刚度降低越快，相同地震作用下对应的动态位移响应也越大。需要说明的是，混凝土坝动态断裂过程非常复杂，每个时间步的裂缝扩展步长没有实测资料可供参考，故本文仅假定了不同的裂缝扩展步长以研究其影响，可能与大坝实际地震断裂过程存在偏差。

6 结论

将比例边界有限元法(SBFEM)和多边形局部网格重剖分技术结合提出了一种全自动的重力坝动态断裂分析模型。该方法继承了SBFEM降维和半解析描述裂缝尖端奇异应力场等优点，拓展了SBFEM在断裂分析中的应用，可高精度地求解裂缝动态应力强度因子，实现了重力坝地震断裂的高效模拟。为追踪裂缝路径，仅需增加较少的节点即可实现网格重剖分，无须人工干预，因而具有相当高的分析效率。

以Koyna重力坝为例模拟了重力坝的地震断裂过程，并对模型的网格密度和裂缝扩展步长进行了敏感性分析。结果表明：(1)网格密度对坝体地震响应和裂缝扩展形态影响很小，且较粗的多边形网格即可获得满意的计算结果；(2)裂缝扩展步长取值对大坝最终破坏形态影响不大，但是步长越大裂缝扩展越快，从而导致大坝非线性地震响应存在差别。综上，本文方法可成为混凝土坝地震断裂分析中一种很有竞争力的数值分析技术，后续有望拓展至混凝土界面裂缝以及三维裂缝的动态扩展模拟。