融合时频空间特征的土石坝地震易损性分析改进MLP模型研究
王晓玲,李清梦,刘宗显,余 佳,余红玲,王昊东
(1.天津大学 水利工程智能建设与运维全国重点实验室,天津 300072;2.雅砻江流域水电开发有限公司,四川 成都 610051)
1 研究背景
土石坝地震易损性分析对于抗震设计、抗震加固以及风险评估等方面具有重要意义[1]。地震动指标和大坝地震需求模型建立是土石坝地震易损性分析的两个关键环节[2-3]。然而,现有的土石坝地震易损性分析研究中采用的峰值加速度、峰值速度等地震动指标,未能充分反映地震动的时频空间特征;且既有基于对数空间线性函数关系假设的地震需求模型难以揭示地震动指标与地震响应间复杂非线性关系。因此,亟待构建充分反映地震动复杂时频空间特征的指标,并建立能够揭示地震动指标与地震响应间复杂非线性关系的地震需求模型,在此基础上进行土石坝地震易损性分析,为土石坝抗震风险评估提供支持。
在地震动指标建立方面,现有研究中常用的地震动指标主要分为两类:一类是采用单个指标表征地震动;另一类采用两个及以上的多元地震动指标。在地震动单指标方面,现有研究一般采用谱加速度[4-5]、峰值加速度[6-7]、峰值速度[4,8]和峰值位移[8]等指标开展地震易损性研究。此外,一些新型地震动指标,如考虑结构特征的地震动指标[9]、基于主导模态的地震动指标[10]和多周期平均谱加速度指标[11]等,也被提出用于表征地震动。然而,单个地震动指标所承载的信息有限,只能表征地震动的部分特征。为更充分反映地震动的复杂信息,相关学者提出了多元地震动指标。例如,Alembagheri等[12]基于所提(Sa(T1),PGA)、(Sa(T1),PGD)、(PGA,PGD)和(Sa(T1),Sa(T1)/Sa(Tn)PGA)四种多元地震动指标开展了易损性研究;Baker等[13-15]提出了(Sa(T1),Epsilon)和(Sa(T1),Sa(T1)/Sa(T2))两种多元地震动指标;Fotopoulou等[16]基于充分性和地震动指标间的相关度优选出了(PGA,Ia)和(PGV,Ky/PGV)两种多元地震动指标;范书立等[17]基于多元地震动指标(Sa(T1),Sa(T2))对某拱坝开展了地震易损性分析研究。虽然多元地震动指标相较于单个指标能够反映更多的地震动信息,但是由于地震动具有复杂的时频空间特征,仅通过几个单指标组合而成的多元地震动指标仍然难以对其充分表征[18]。
小波变换凭借其强大的时频分析能力,能够将一维地震动信号映射到二维时频平面获得小波时频图,以充分反映地震动复杂的时频特征[19]。然而,小波时频图所表征的复杂地震动信息隐藏于时频图片中,且地震动信息与其特征在时频图上的空间位置分布有着密不可分的关系。因此,如何考虑小波时频图特征的空间位置分布关系,并对其进行特征提取是亟待解决的问题。胶囊网络不仅具有很强的特征提取能力,同时能够学习特征之间的空间位置关系,已经在航空航天[20]、遥感影像[21]、故障检测[22]等领域得到了广泛的应用,为提取小波时频图中复杂时频空间特征提供了有效途径。因此,本文采用胶囊网络对地震动小波时频图进行特征提取,以获得能够反映地震动时频空间分布的深层特征;进一步,采用特征拼接的方式将地震动深层时频空间特征与既有特征(峰值加速度、峰值速度等)进行融合,获得地震动融合指标,以充分揭示地震动的复杂时频空间特征。
在大坝地震需求模型建立方面,现有研究大多假设地震动指标与地震响应间服从对数空间线性函数关系,难以揭示地震动指标与地震响应间复杂非线性关系[23]。MLP神经网络具有强大的数据自驱动能力和对高维非线性问题的处理能力,近年来在抗震评估[24]、数据去噪[25]、趋势预测[26]等领域得到了广泛应用,为揭示地震动指标与土石坝地震响应间的复杂非线性关系提供了新途径。MLP神经网络中神经元数量、学习率等超参数的选取直接影响其性能[27],现行手动调参方式存在精度与效率低的问题。TPE优化算法具有优化机制简单、收敛速度快和鲁棒性强等优势,能够利用先验知识高效地优化MLP的超参数。因此,采用TPE优化算法对MLP的超参数进行自动寻优,进而建立TPE-MLP土石坝地震需求模型,以提高模型的精度和构建效率。
综上所述,为了充分反映地震动复杂时频空间特征,并揭示地震动指标与地震响应间复杂非线性关系,提出一种融合时频空间特征的土石坝地震易损性改进MLP模型。其中,采用CapsNet和小波变换构建地震动时频空间特征融合指标,以充分反映地震动复杂时频空间特征,并提出基于TPE改进MLP的土石坝地震需求模型,以准确揭示地震动融合指标与土石坝地震响应间的复杂非线性关系,进而实现可靠的土石坝地震易损性分析。
2 研究框架
所提融合时频空间特征的土石坝地震易损性改进MLP模型研究框架如图1所示,具体如下:
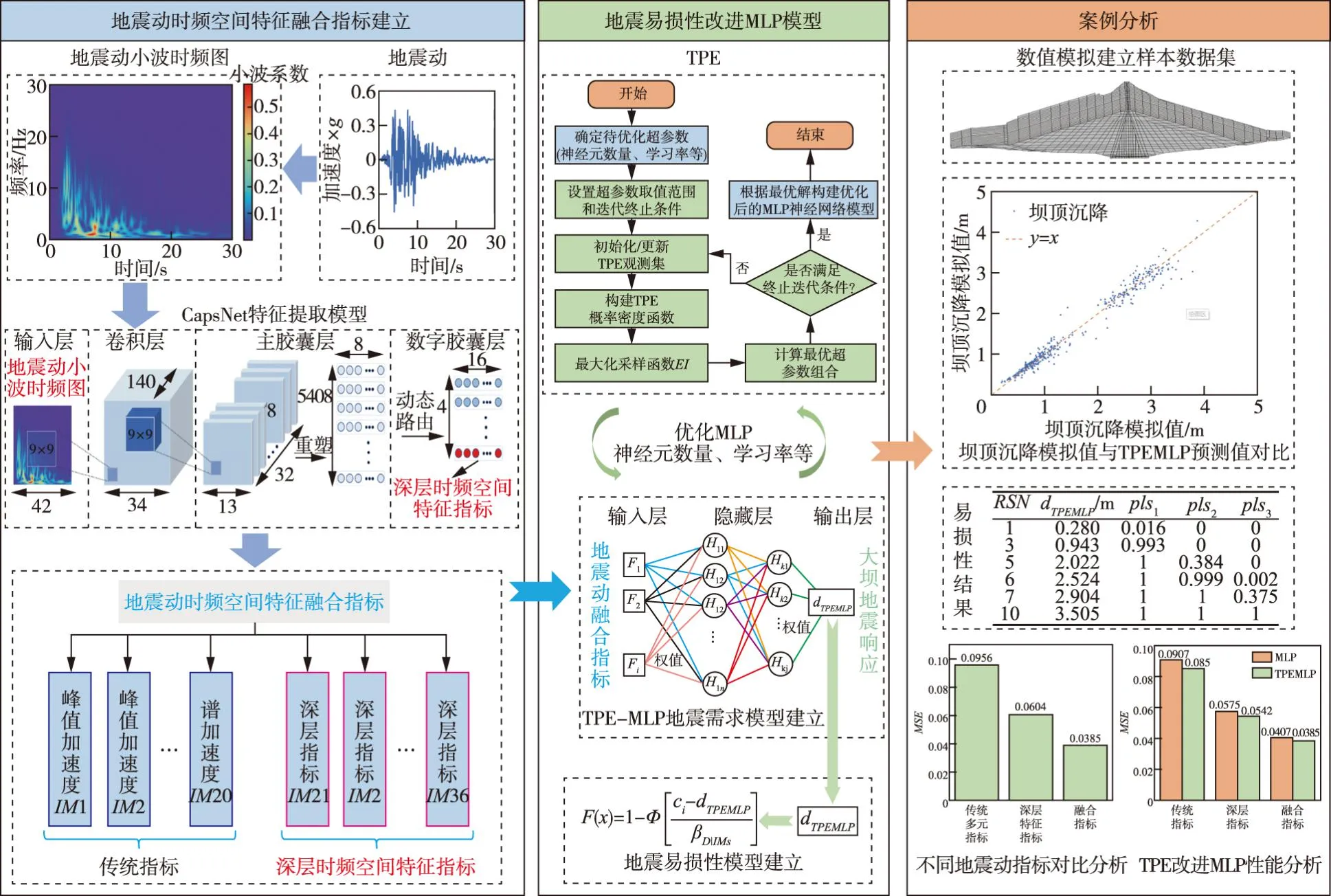
图1 研究框架
(1)地震动时频空间特征融合指标建立。采用CapsNet对地震动小波时频图进行特征提取获得地震动深层时频空间特征,并与既有特征进行融合获得地震动时频空间特征融合指标。
(2)地震易损性改进MLP模型。采用TPE优化MLP网络模型的神经元数量、学习率等超参数,建立TPE-MLP土石坝地震需求模型,以反映地震动融合指标与地震响应间的复杂非线性关系,进而构建地震易损性改进MLP模型。
(3)案例分析。将所提模型应用于工程实例,并对比基于融合指标、深层指标、既有指标的坝顶沉降预测结果,以及基于TPE-MLP与基于MLP的坝顶沉降预测结果,从而验证所提模型的可靠性和优越性。
3 融合时频空间特征的土石坝地震易损性改进MLP模型
3.1 基于小波变换和CapsNet的地震动时频空间特征融合指标构建方法
3.1.1 基于小波变换的地震动时频图构建方法 为了表征地震动的时频空间特征,采用小波变换将一维的地震动信号映射到二维的时频平面,获得能够同时表征地震动时、频域特征的小波时频图。
假设x(t)表示地震动信号,ψ(t)表示基本小波,则地震动信号的小波变换WTx(a,τ)可表示为:
(1)
式中:t为时间;τ为位移因子;a为尺度因子;ψ*为ψ的共轭复数。
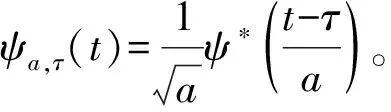
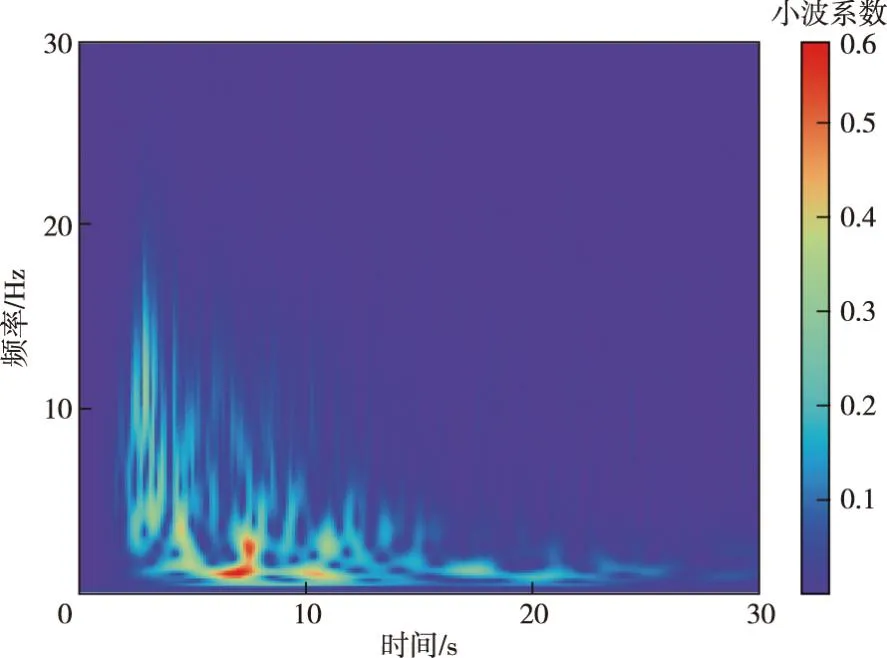
图2 地震动小波时频图
3.1.2 地震动时频空间特征融合指标构建方法 CapsNet是Hinton等[28-29]于2017年提出的一种新型神经网络,其核心思想是采用矢量形式的胶囊编码特征对象信息,使其不仅具有很强的时频特征提取能力,而且具有充分捕捉和表征时频特征空间位置分布的优势。其中,胶囊的模长和方向分别编码了地震动时频特征的存在概率与实例化参数,并采用仿射变换和动态路由传递时频特征的空间位置信息,其结构如图3所示。
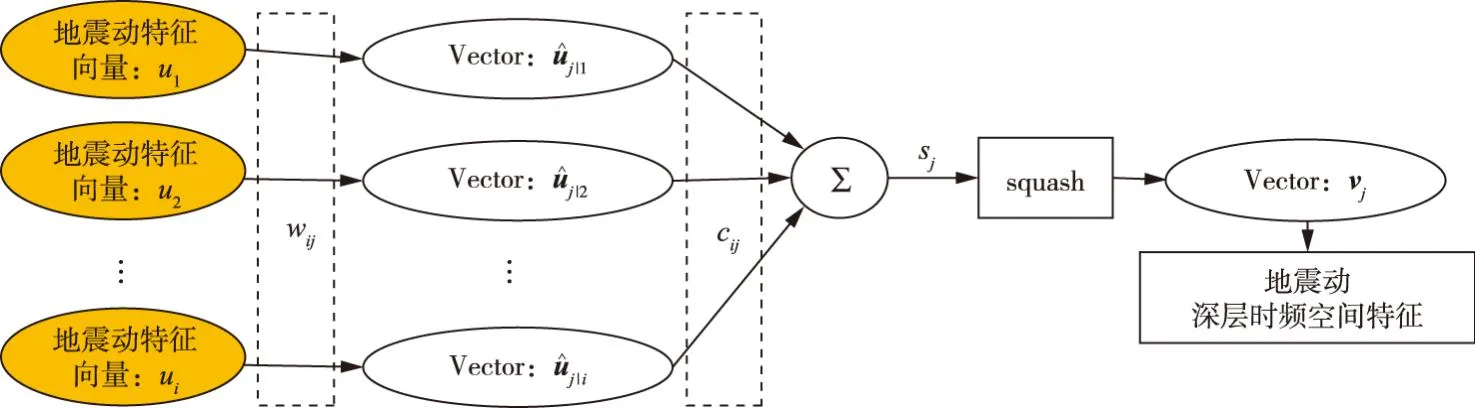
图3 胶囊神经元结构
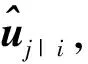
(2)
式中:低层地震动特征向量ui是指地震动小波时频图经卷积运算获得的特征;空间变换矩阵Wij是通过误差的反向传播更新获得。
(3)
再者,采用激活函数squashing对sj进行缩放的同时保证方向不变,获得高层胶囊神经元vj,即地震动深层时频空间特征,如式(4)所示。
(4)
最后,所构建CapsNet模型结构如图4所示,通过卷积层对输入的小波时频图进行特征图提取,进而经过主胶囊层重塑产生矢量胶囊,最后经动态路由将信息传递至数字胶囊层并提取获得深层特征。
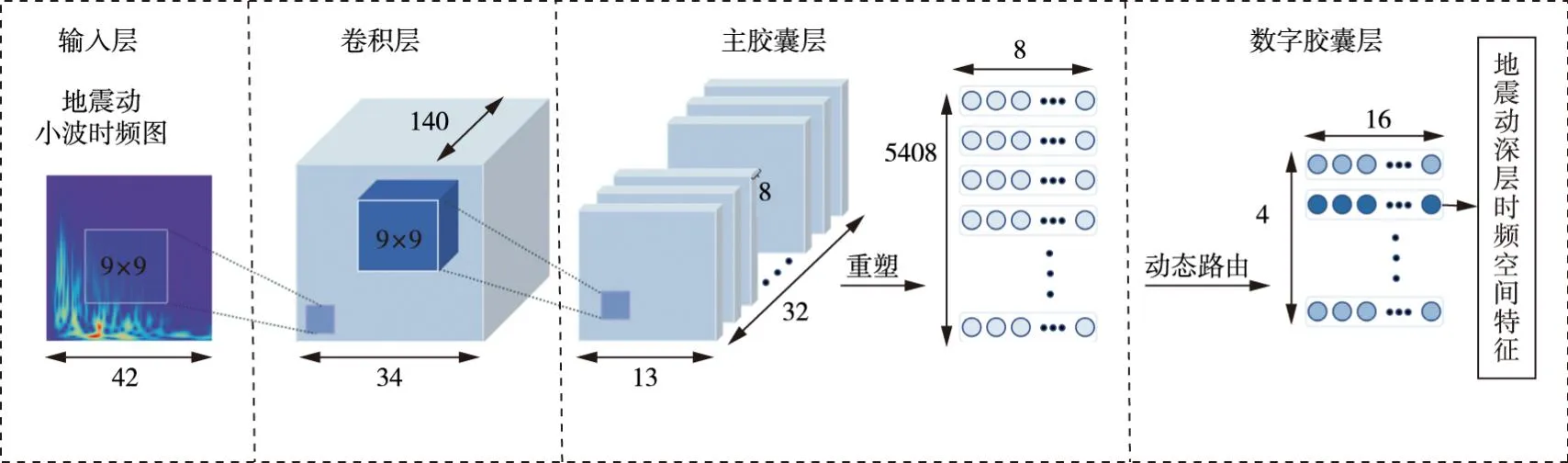
图4 胶囊网络结构
3.1.3 地震动时频空间特征融合指标构建 在地震动深层时频空间特征的基础上,采用特征拼接的方式将其与既有特征进行融合获得地震动时频空间特征融合指标。其中,地震动既有指标是参考相关研究[13-17],并以全面性、计算效率和可获得性为原则进行确定,见表1。这些指标涵盖了地震动的峰值、频谱和持时三个方面特性,其中反映地震动峰值特性的指标有PGA、PGV、PGD、CAV,反映地震动持时特性的指标有Td、IA、Pa,反映地震动频谱特性的指标有SI、PSA、PSV、PSD、Saavg、Svavg、Sdavg、ASI、VSI、DSI、EPA、EPV、EPD。

表1 地震动既有指标
3.2 基于TPE-MLP的土石坝地震需求模型建立方法MLP神经网络具有强大数据自驱动能力和对高维非线性问题的处理能力,能够充分揭示地震动与土石坝响应之间的高维非线性关系。然而,MLP神经网络中隐藏层神经元数量、学习率等超参数的选取直接影响网络的性能,传统手动调参的方式存在精度不高且效率低下的问题。TPE优化算法能够利用先验知识高效地优化超参数,具有优化机制简单、收敛速度快和鲁棒性强等优势。因此,采用TPE优化算法对MLP的超参数进行自动寻优,进而构建土石坝地震需求TPE-MLP模型。
TPE优化算法采用预期改进(Expected Improvement,EI)构建采样函数(Acquisition Function),通过在每次迭代中返回具有最大EI值的超参数,搜索获得MLP最优超参数,EI的定义如下式所示:
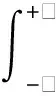
(5)
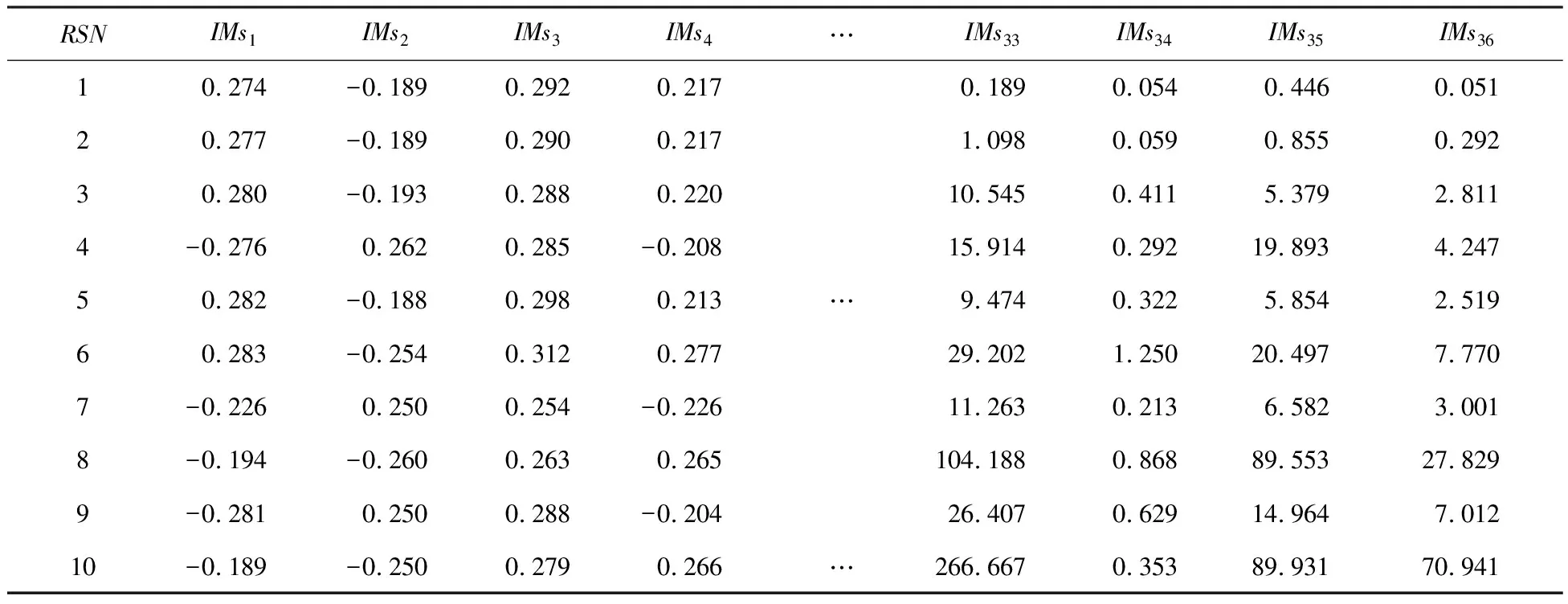
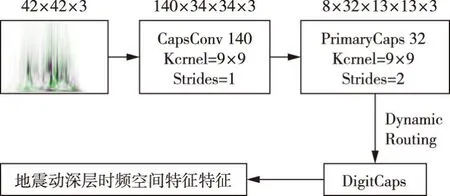
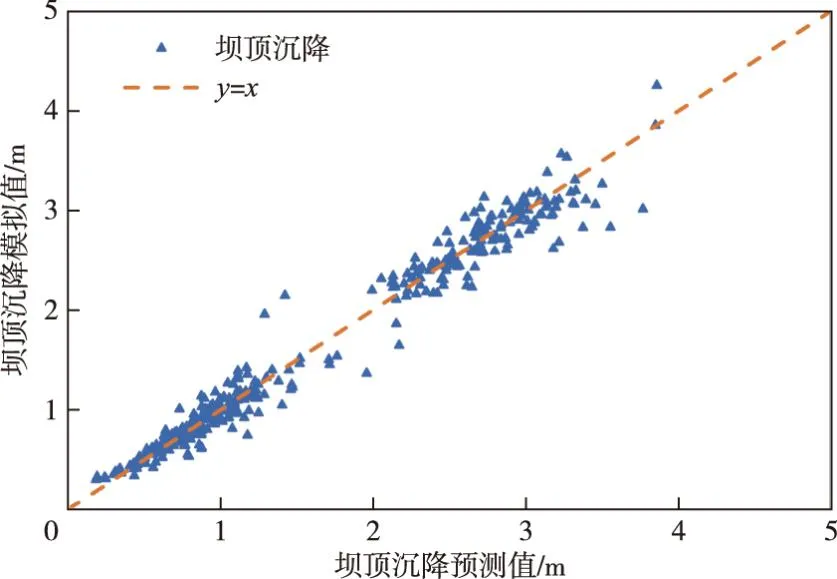
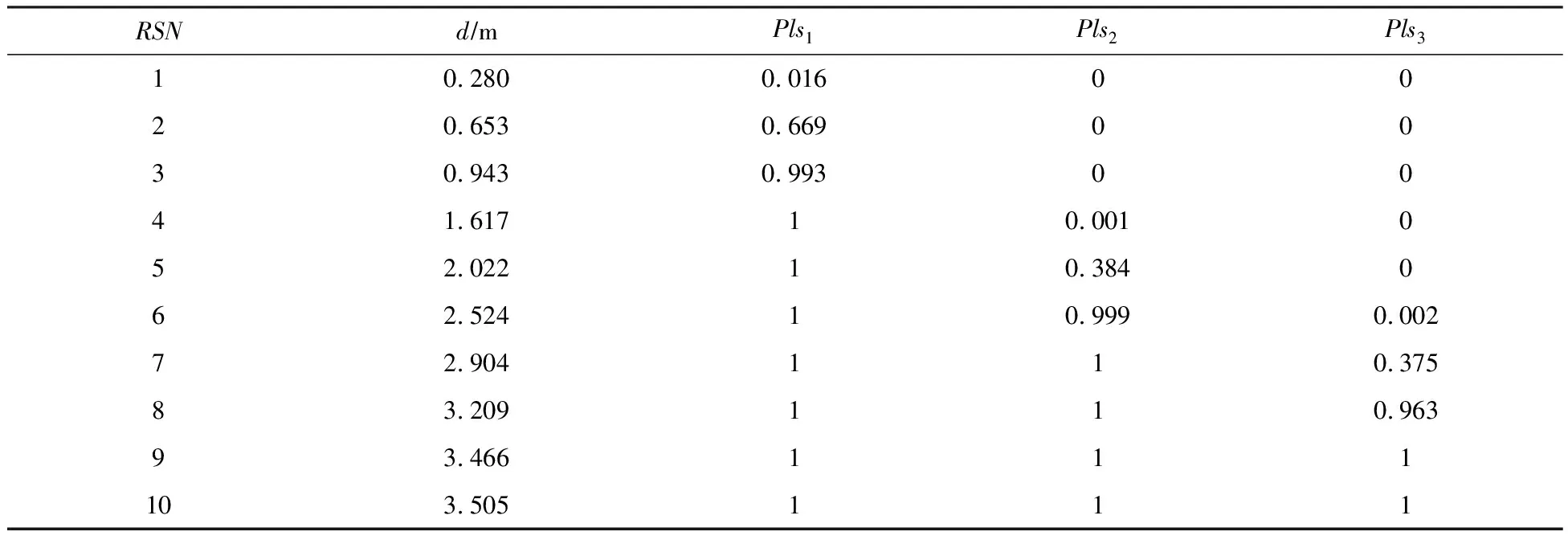
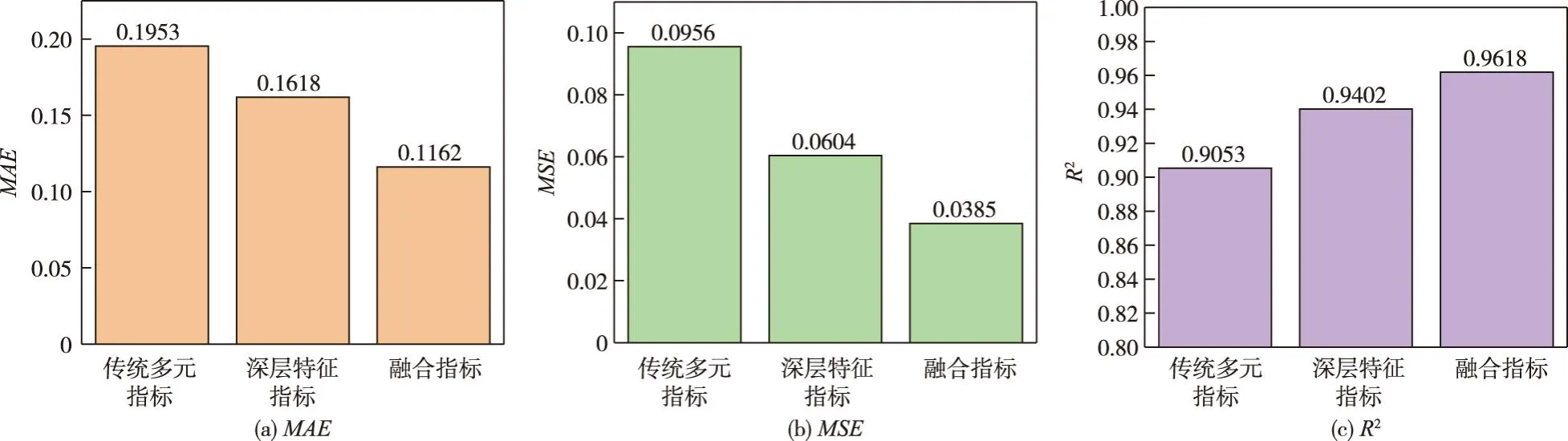
式中:x为多层感知机神经网络的超参数,即隐藏层神经元数量、学习率和激活函数;y为x的目标函数值,即MLP网络的损失;y*为最佳观察分界点,通过设置的超参数γ=P(y TPE优化算法对P(x|y)进行如下建模: (6) 进而基于贝叶斯定理和γ=P(y P(x)=γl(x)+(1-γ)g(x) (7) 最后基于P(x|y)和P(x)表达式,可对EI进行如下变形: (8) 由式(8)可知,在每次迭代过程中,通过最小化比值g(x)/l(x)取得最大化的EI值,从而获得最优的MLP超参数组合。 采用数值模拟方法获得不同地震动作用下的土石坝响应,建立土石坝地震响应样本数据集,进而对TPE-MLP神经网络进行训练,构建基于TPE-MLP的土石坝地震需求模型,构建流程如图5所示。 图5 TPE优化MLP超参数流程图 3.3 基于地震动时频空间特征融合指标和TPE-MLP地震需求模型的地震易损性模型土石坝地震易损性表示在不同地震动强度下,大坝结构达到或超越不同破坏等级极限状态的条件概率[30],即在某一地震强度作用下,土石坝结构地震需求超过其抗震能力的概率,定义如下: F(x)=P[D≥C|IMs] (9) 式中:IMs为地震动时频空间特征融合指标;F(x)为地震易损性函数;C为土石坝抗震能力;D为土石坝地震需求。 土石坝地震需求D表达式如下: D=dTPEMLP+ε (10) 式中:dTPEMLP为土石坝地震响应TPE-MLP预测值;ε为随机误差,假设其服从标准差为σD|IMs的正态分布。 基于式(9)和式(10)可推得地震易损性函数F(x)表达式: (11) 式中ci(i=1,2,3)为破坏等级极限状态,参考相关土石坝震害破坏等级划分研究[6,7],采用坝顶沉降表征土石坝地震响应,坝顶沉降率0.3%、0.6%、1%作为破坏等级划分标准,分别对应轻度破坏(c1)、中度破坏(c2)和重度破坏(c3)三种破坏等级。 以西南某土石坝为研究对象进行应用分析。大坝主体为砾石土心墙土石坝,坝顶高程为2875 m,最大坝高为295 m,坝顶长度为650 m。大坝地处横断山脉,是印度洋板块和亚欧板块碰撞的交汇处,正处于地震带上。采用所提模型对该土石坝进行地震易损性分析,为其抗震风险评估提供有效手段和必要依据。 4.1 地震动时频空间特征融合指标建立采用基于python的小波变换函数依次对地震动加速度时程数据进行时频分析,获得每个地震动对应的小波时频图,如图2所示。其中小波变换函数参数设置如表2所示。 表2 小波函数参数设置 采用CapsNet对小波时频图进行特征提取,获得反映地震动时频空间分布的深层特征。图6展示了胶囊网络参数设置,图中CapsConv表示卷积层,PrimaryCaps表示主胶囊层,DigitCaps表示数字胶囊层。以10条从PEER开源地震数据库获得的地震动为例,基于表1中的公式计算获得每条地震动的20维既有特征,并将其与16维深层时频空间特征进行特征拼接,建立36维地震动时频空间特征融合指标,如表3所示,表中IMsr(r=1,2,…,16)表示16维深层时频空间特征,IMsc(c=17,18,…,36)表示20维既有特征,表中RSN表示地震动编号,由于篇幅有限仅展示了部分指标。 表3 地震动融合指标 图6 胶囊网络参数设置 4.2 土石坝地震需求模型建立与结果分析 4.2.1 土石坝地震需求模型样本生成 采用三维动力有限元计算获得不同地震动作用下的坝顶沉降,生成土石坝地震需求模型的样本。首先,构建大坝三维有限元模型,该模型主要采用六面体八节点单元进行网格划分,少数不规则处采用四面体单元进行网格划分。其次,采用邓肯张模型表征大坝主体材料的非线性本构特征,采用等效黏弹线性模型和沈珠江模型模拟地震动对大坝造成的坝顶沉降[31],材料模型参数如表4和表5所示。最后,以地震动加速度幅值在0.01g~1g区间内较为均匀地分布为原则,从PEER开源地震数据库筛选获得的1521条三向地震动加速度时程,将其作为边界条件施加到大坝有限元模型进行非线性时程分析,获得大坝在地震动作用下的坝顶沉降。进一步,建立地震动-坝顶沉降样本数据集。 表4 邓肯张模型参数 表5 动力计算模型参数 4.2.2 土石坝地震需求模型建立与分析 采用参数优化器Hyperopt实现TPE算法对MLP神经网络超参数的优化。首先,初始化Hyperopt参数,最小化目标为模型均方误差;最大迭代次数为500,搜索算法为tpe.suggest。其次,设置多层感知机神经网络的初始参数,隐藏层数量为2,隐藏层神经元数量搜索空间为4~1024,激活函数搜索空间为tanh、sigmoid、relu,学习率搜索空间为0.00001~0.1。最后,随机选取1140组地震动-坝顶沉降样本作为训练集对TPE-MLP模型进行训练,剩余的381组样本作为测试集测试TPE-MLP模型的性能。经TPE优化MLP最优超参数为隐藏层神经元数128×512,学习率0.00005,激活函数relu。 图7给出了在测试集上坝顶沉降模拟值与TPE-MLP预测值的对比结果,样本点越靠近图中虚线y=x说明模型精度越高。可以看到,坝顶沉降模拟值与预测值之间平均绝对百分比误差(MAPE)为8.64%,基本保持在直线y=x附近,表明TPE-MLP能够较好地建立地震动与坝顶沉降之间的非线性关系,准确高效地获得不同地震动作用下的坝顶沉降值。 图7 坝顶沉降模拟值与预测值对比 4.3 土石坝地震易损性分析采用所提模型对西南某土石坝进行地震易损性分析。该土石坝的地震易损性是地震融合指标(IMs1,IMs2,…,IMs36)的函数,最终获得的不是传统形式的易损性曲线,而是一个在36维空间上的超平面。为了清楚表达土石坝地震易损性,以10条覆盖了土石坝发生不同破坏等级概率从0到1变化过程的地震动为例,将易损性分析结果以表格的形式展现,如表6所示。表中地震动编号RSN与表3中对应,dTPEMLP表示TPE-MLP土石坝沉降预测值,Plsi(i=1,2,3)分别表示大坝发生轻度破坏(c1)、中度破坏(c2)和重度破坏(c3)的概率。 表6 地震易损性分析结果 4.4 对比分析与讨论 4.4.1 不同地震动指标对比分析 将所提基于融合指标的坝顶沉降预测结果分别与基于既有指标、深层指标的坝顶沉降预测结果进行对比分析,以验证融合指标的可靠性和优越性。其中,用于坝顶沉降预测的TPE-MLP均采用相同的网络结构,即:学习率为0.00005,激活函数为relu,隐藏层层数为2,隐藏层神经元数分别为128和512。 采用平均绝对误差(MAE)、均方误差(MSE)和决定系数(R2)三个指标来评价三种地震动指标下的坝顶沉降预测结果。由图8可以看出,基于三种地震动指标的预测结果表现出一致性,MAE均小于0.2,MSE均小于0.1,R2均大于0.9,表明了融合指标的可靠性。相比于既有指标和深层指标,所提基于融合指标的地震响应预测结果的MAE分别降低了40.5%和28.2%;MSE分别降低了59.7%和36.3%;R2分别提高了6.24%和2.29%。表明融合指标具有良好的可靠性和优越性,能够充分揭示地震动复杂时频空间特征,提升坝顶沉降预测结果的准确性。 图8 不同地震动指标下预测性能对比 4.4.2 TPE改进的MLP模型性能分析 基于地震动融合指标,分别采用TPE-MLP与MLP模型进行坝顶沉降预测,以验证TPE改进MLP的优越性。TPE优化前后MLP模型超参数与性能指标如表7所示。 表7 TPE优化前后MLP模型性能对比 表7表明,经TPE优化MLP后,模型的MAE降低了7.48%,MSE降低了5.41%,R2提高了0.22%。表明TPE优化的MLP模型性能更优,进一步提升了土石坝地震需求分析的准确性。 针对现有研究采用的地震动指标未能充分反映地震动复杂时频空间特征,以及传统地震需求模型难以揭示地震动指标与地震响应间复杂非线性关系的问题,提出一种融合时频空间特征的土石坝地震易损性改进MLP模型,主要结论如下: (1)提出了基于小波变换和CapsNet的地震动时频空间特征融合指标构建方法。在采用小波变换获得地震动小波时频图的基础上,采用CapsNet对小波时频图进行特征提取,获得了反映地震动时频空间分布的深层特征;进一步,采用特征拼接方式将地震动深层时频空间特征与峰值加速度、峰值速度等既有特征进行融合,获得地震动时频空间特征融合指标,弥补了既有地震动指标未能充分反映地震动复杂时频空间特征的不足。 (2)建立了基于TPE改进MLP的地震需求模型。采用TPE优化MLP的神经元数、学习率等超参数,提升了MLP的网络精度和建模效率,揭示了地震动指标与地震响应间复杂非线性关系。 (3)将所提模型应用于西南某土石坝地震易损性分析中。相比于既有地震动指标,基于地震动融合指标的土石坝地震需求模型的MAE降低了40.5%;相比既有MLP,基于TPE优化MLP的土石坝地震需求模型的MAE降低了7.48%,表明了所提模型的可靠性和优越性,有效提升了土石坝地震需求模型的精度,进而确保了土石坝地震易损性分析结果的可靠性。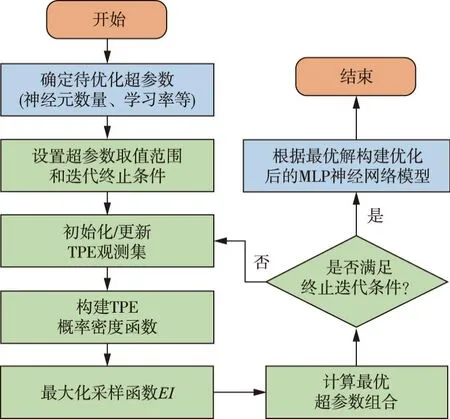
4 案例分析




5 结论

