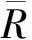金沙江下游三堆子河段卵石推移质输沙率公式研究

冯志毅，邓安军，秦蕾蕾，吕瑞茹

(1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100048；2.中国水利水电科学研究院 水利部泥沙科学与北方河流治理重点实验室，北京 100048；3.中国三峡建工(集团)有限公司，四川 成都 610041)

金沙江水能资源丰富，是我国最大的水电基地之一。金沙江上游(川藏段)规划岗托、岩比水电站等8个梯级电站；中游按照“一库八级”进行开发，鲁地拉、观音岩水电站等陆续投产使用；下游干流乌东德—白鹤滩—溪洛渡—向家坝梯级水库均已建成投运[1]。天然条件下，金沙江中游出口控制站攀枝花站年平均悬移质输沙量约为6632万t[2]；随着金沙江上中游干支流水库的建设运行，进入下游河道的泥沙大幅度减少，攀枝花站(2011—2021年)年均输沙量仅为梯级水库运行前的9%。考虑到下游入口河段床沙组成较粗，基本由卵石和基岩组成，径流冲刷作用下卵石推移质输沙量将沿程增加。金沙江下游属于典型的山区河流，水土流失严重，滑坡和泥石流频发，推移质输沙量大，淤积后会造成多方面危害：减少有效库容，影响梯级电站综合效益；抬高库尾水位，减少上游梯级发电水头；在水库淤积后期，推移质一旦过坝，会对泄水建筑物和发电机组等产生破坏作用。数据表明，我国水库平均淤损率已达11.27%[3]，因此推移质在梯级水电站开发运行过程中亦不容忽视。

目前，国内外学者从不同角度对推移质起动展开深入研究，如起动拖曳力、起动流速和起动功率等，提出了不同的临界起动公式。长江上游推移质起动公式多采用起动流速，张植堂等[4]总结了我国学者在长江上游卵石推移质起动流速上取得的成果，卢金友[5]、冷魁[6]等也针对卵石起动流速开展了系列工作；何文社[7]在引入附加质量力和等效粒径的基础上，从力学角度和几何学角度得到了泥沙颗粒临界起动流速公式。

此外，在推移质输沙方面，自Duboys[8]首次提出基于拖曳力理论建立推移质输沙率公式后，国内外学者从多个角度提出了各自的输沙率公式，代表性成果包含：以Meyer-Peter[9]为代表的根据大量实验数据建立的推移质公式；以Bagnold[10]为代表的依据物理学的基本概念并通过一定力学分析建立的推移质公式；以Einstein[11]为代表的采用概率论及力学相结合的方式建立的推移质公式；以Engelund[12]及Yalin[13]为代表的，在Einstein或Bagnold的某些概念的基础上辅以量纲分析、实测资料适线以及一定的推理建立的推移质公式。据不完全统计，目前各种推移质输沙率公式已超过50个，但由于问题的复杂性，至今还没有一个公认的能精确预测推移质输沙率的计算式。

针对长江上游卵石推移质输移规律研究取得了很多的成果，如朱南华等[14]通过分析长江上游卵石推移质基本物理要素，结合实测及试验资料阐明了卵石推移质的运动方式；彭润泽[15]、王兴奎[16]、张之湘[17]、曹叔尤[18]、金中武[19]、卢金友[20]、魏丽[21]等分析实测资料后，提出了适用于长江上游的推移质输沙公式；尹晔等[22]依据模型试验分析了金沙江下游梯级电站出口的推移质输沙规律；侯新[23]、张娜[24]通过分析三堆子站实测卵石推移质资料，研究了金沙江下游推移质的年内分布、级配特征。

上述研究主要针对自然条件下的卵石推移质输移规律，但近年来金沙江上中游梯级水库的拦沙作用，导致下游水沙情势发生显著变化。变化水沙条件下，金沙江下游卵石推移质输移规律仍需进一步研究；加之推移质运动复杂，已有经典公式的计算结果也存在较大的差异。因此亟须对金沙江下游卵石推移质起动及输沙量展开研究，揭示变化水沙条件下河道内推移质的输移演变规律，提出适用于金沙江下游的卵石推移质起动及输沙公式。

1 研究区域及资料方法

1.1 研究区概况及资料金沙江为长江上游干流河段，以云南石鼓、四川攀枝花为界分为上、中、下游。下游河段自攀枝花至宜宾，长约768 km，落差719 m。河段入口处建有三堆子水文站(图1)，位于金沙江下游与其支流雅砻江汇口以下4.00 km处左岸，距下游乌东德水电站坝址196 km，附近河段比较顺直，河床组成基本为卵石和基岩。

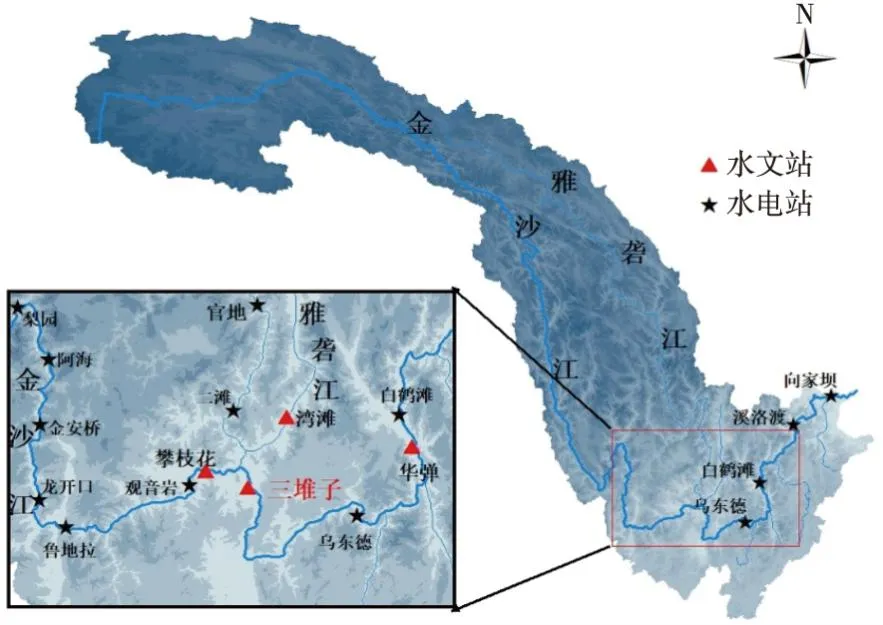
图1 研究区域位置示意图

三堆子站自2007年以来持续开展了卵石推移质的现场测验工作。卵石推移质全年测次总数不少于80次，测次布置按照过程线法控制，现场进行样品级配筛分，至2021年已收集738组次的卵石推移质泥沙运动原型观测资料。2021年乌东德水电站投产运行，非汛期运用水位975 m，回水虽能够到达三堆子河段，但非汛期流量小，基本没有卵石推移质的运动；防洪限制水位为952 m，汛期水位较低，回水不会影响至三堆子水文站。资料中主要的水流及泥沙要素统计见表1。

表1 三堆子站实测资料统计

1.2 研究方法本文采用分散度R及Nash-Sutcliffe效率系数NSE值对修正公式精度进行定量评价，具体方法将在下文分别进行介绍。

1.2.1 分散度 参照金中武等[19]的方法，分散度定义如下：

R=xbc/xbm

(1)

式中x为系列值，包括起动流速和输沙强度，xbc为公式计算值，xbm为实测值。

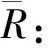
(2)

式中：i表示组次；n表示资料总数。对于起动流速，统计R值在<0.8、0.8～<0.9、0.9～<1、1～<1.1、1.1～<1.2、≥1.2区间的分布情况，将R值在0.9～1.1区间的百分数作为评判公式精度的标准，并将R值在<0.8和≥1.2区间的百分数作为资料的排除率。

输沙强度由于受到多种因素的影响，利用R值评判公式精度时应适当放宽标准，因此统计各公式R值在<0.1、0.1～<0.5、0.5～<1、1～<2、2～<10、≥10区间的分布情况，将R值在0.5～2区间的百分数作为评判公式精度的标准，并将R值在<0.1和≥10区间的百分数作为资料的排除率。

1.2.2 Nashi-Sutcliffe效率系数 Nashi-Sutcliffe效率系数NSE值是判定残差与实测值数据方差相对量的标准化统计值，计算公式如下：

(3)

式中NSE为Nashi-Sutcliffe效率系数。NSE值一般在-∞～1.0之间，当NSE=1.0时表明计算值与实测值完全吻合，当NSE>0.5时说明计算结果在可接受的水平内，当NSE>0时表明计算结果有效，当NSE≤0时说明计算值与实测值存在较大偏差。

2 三堆子河段新水沙情势及卵石推移质输沙特性

2.1 新水沙情势根据三堆子站2008—2021年实测水沙资料，绘制金沙江下游径流量及输沙量的年际过程(图2)。结果表明，研究时段内金沙江下游径流量未发生趋势性变化，2008—2011年径流量逐年减少，至2011年达到最小值884亿m3；随后呈现波动上升趋势，至2018年达到最大值1379亿m3，整体在多年平均值1139亿m3上下波动。

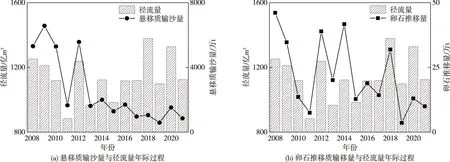
图2 三堆子站径流量与输沙量年际过程

鉴于金沙江中游梯级电站自2012年以来陆续蓄水运行，本文将研究时段划分为2008—2012年和2013—2021年，分析不同时段金沙江下游径流过程的变化。根据三堆子站2008—2021年日均流量过程，以2000 m3/s为一级，统计前后两时段各流量级出现的平均天数(表2)。由表2可见，自金沙江上中游梯级水电站运行后，由于梯级水库拦洪削峰，2000 m3/s以下的小流量和10 000 m3/s以上的大流量发生的频率减小，其中大流量级出现的平均天数由2008—2012年的20.2 d减小至2013年以后的12.0 d，减幅为40.6%；对应时段2000～10 000 m3/s发生的频率则显著增大，由年均168.8 d增加为2013年以后的215.8 d，增幅为27.8%。新水沙情势下金沙江下游径流过程的重分配效应明显。

表2 三堆子站各时段特征流量平均天数统计 (单位：d)

如图2(a)所示，悬移质输沙量呈现显著减小趋势，每年约减少318万t，研究时段内输沙量年际极值比达6.8；图2(b)表明，卵石推移量除2012年和2014年增大幅度明显外，其余年份输沙量呈周期性减小趋势。金沙江降水和径流之间存在良好的相关关系[25-26]，2012年及2014年金沙江流域降水量增大，引起径流量增大，使其对应年份输沙量变大，这也是卵石推移量激增的原因。同时，2014年金沙江干流降水量较2012年多[27]，但2014年径流量及悬移量增幅却远小于2012年，这是因为自2012年以来，金沙江中游鲁地拉、观音岩等电站陆续投产使用，不但减少了上游来水量，亦拦截了大量细泥沙，使得上游悬移质泥沙补给显著减少。

2.2 卵石推移质输沙特性变化统计三堆子站前后两时段内输沙量组分均值变化及占比情况(表3)。结果表明，2013—2021年多年平均卵石推移量由2008—2012年的28万t减小至2013年以后的19万t，相应时段内悬移质输沙量由4880万t锐减至1288万t，卵石推移质输沙量及悬移质输沙量减幅分别为32.1%和73.6%，对应时段内卵石推移质输沙量占总输沙量的比例由0.6%增大至1.5%，三堆子河段卵石推移质输沙量的占比有增大趋势。可见变化水沙情势下卵石推移质在该河段河床演变过程中的影响日益显著。

表3 三堆子站不同时段输沙量组分变化情况

3 三堆子河段卵石推移质起动流速公式

3.1 经典起动流速公式检验鉴于天然河流难以取得精确的水力坡降成果，目前泥沙起动条件多采用起动流速为参数的表达方式。依据前人的研究成果，泥沙起动受到各种力的综合作用，基于滚动模式下受力平衡，推导得到起动流速公式基本结构如下：

(4)

式中：Uc为卵石起动流速，m/s；h为断面平均水深，m；d为泥沙粒径，m；γ、γs分别为水和泥沙颗粒的容重，本文分别取为9800 N/m3和25 970 N/m3；g为重力加速度，m/s2；K、m为待定系数。

为了更有效地反映三堆子站卵石推移质起动规律，依照前人研究方法[4，21，28]，取实测卵石推移质最大粒径dmax为相应水流条件下的临界起动粒径，对应的流速也即该粒径的起动流速，故式(4)改写为

(5)

对于参数K和m，各家公式取值略有不同，经典起动流速公式通常将系数K及指数m取为常数，如沙莫夫取K=1.14，m=1/6；武汉水利电力学院K=1.34，m=0.14。

考虑到三堆子站实测卵石推移质资料中最大粒径dmax的范围是8～307 mm，差别较大，因此将dmax分为小粒径组(dmax<100 mm)、中等粒径组(100 mm≤dmax<200 mm)和大粒径组(dmax≥200 mm)。基于已有实测资料，分别计算经典公式(式(5))的系数K和指数m，并将公式计算结果与实测资料进行比较，结果如图3所示。

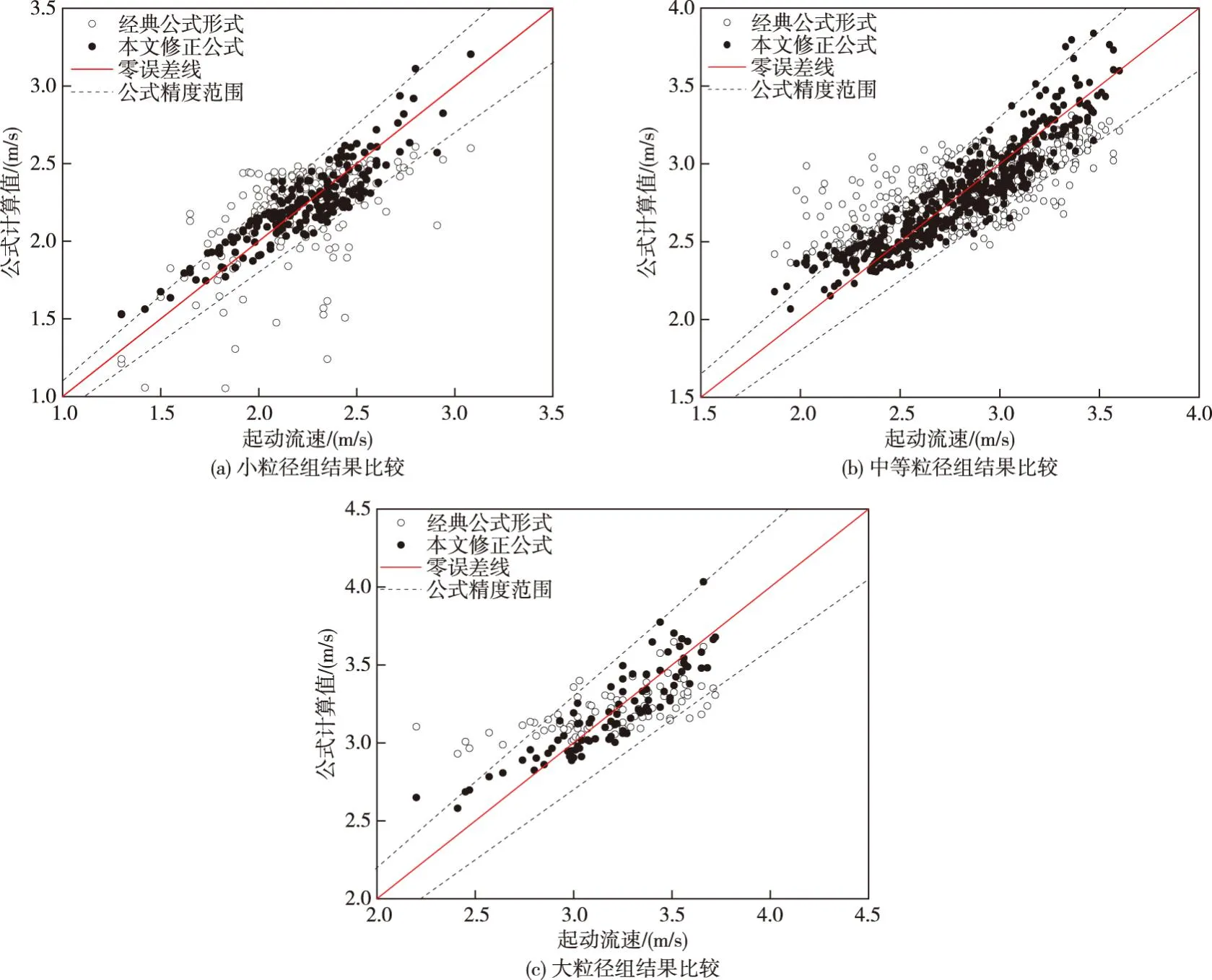
图3 公式计算值与起动流速结果比较

由图3可见，经典公式的计算结果与实际起动流速差别较大。对于小粒径组，公式计算结果在流速1.8～2.7 m/s范围内较为散乱，偏离精度范围(0.9≤R<1.1)的点据较多；中等粒径组和大粒径组的点据相较于小粒径组较为集中，但均存在小流速时计算结果偏大、大流速时计算结果偏小的现象。结果表明，直接将系数K和指数m取为常数的做法，不能很好地反映三堆子河段卵石推移质的起动规律。

3.2 经典起动流速公式修正式(5)是从床面颗粒受力平衡的角度推导得出的，对于均匀沙一般采用这一形式。对于宽级配卵石推移质而言其起动条件更加复杂，具有与均匀沙不同的运动特性，如细颗粒受到粗颗粒的隐蔽、保护作用，粗颗粒则因暴露作用而经受较大的水流作用力。因此对于卵石河床，系数K和指数m取为常数并不能反映非均匀沙颗粒间的隐暴作用，需做出相应改变。

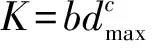
(6)

从式(6)的结构来看，起动流速Uc与最大粒径dmax的关系并不显著，拟合指数值较小，同时与经典公式形式的指数值相比亦偏小。这可能是非均匀沙中粗颗粒的暴露作用导致的。目前对于非均匀沙起动研究的结论一般认为：粗颗粒由于受到暴露而经受较大的水流作用，因此相较于同粒径的均匀沙更容易起动。由于经典公式多是基于室内水槽试验资料得来的，一般按照粒径级分组进行，因此每组试验的河床条件相当于均匀卵石组成的河床[4]。对于天然卵石河流，床沙级配较宽，常包括几个数量级。根据三堆子水文站附近河段2008年5月15日实测的床沙级配，13个测次床沙粒径在2～306 mm，中值粒径d50在104 ～ 244 mm之间，属于典型的宽级配卵石河床(见图4)。因此，在考虑隐暴作用对卵石颗粒起动影响的基础上，本文拟合公式的dmax指数值尚小于经典起动流速公式的指数值，也是合理的。

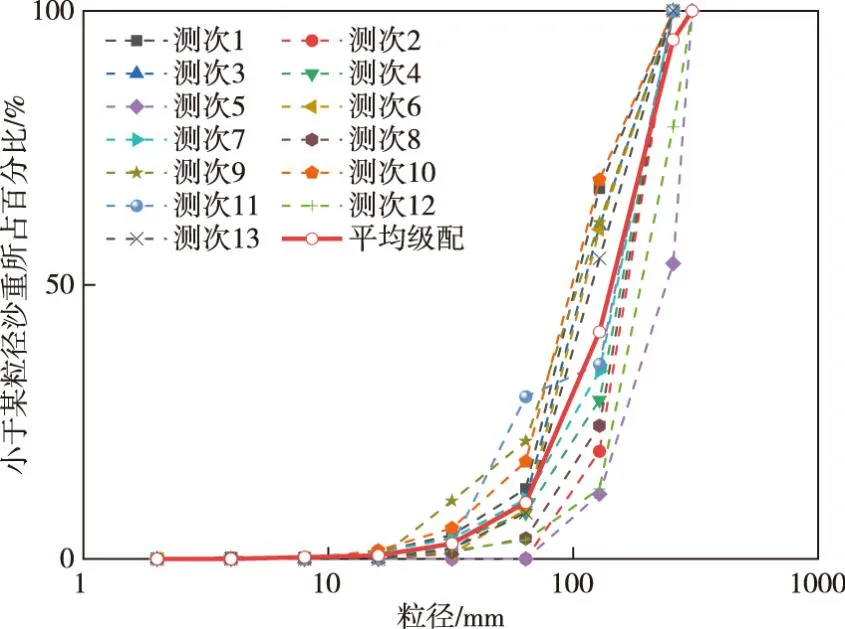
图4 三堆子河段床沙级配

利用式(6)计算结果与实测值及经典公式进行对比，并采用分散度R和Nashi-Sutcliffe效率系数NSE值量化各公式精度，结果见图3及表4。图3结果表明，本文修正公式的计算结果均匀地分布在零误差线两侧，点据多位于分散度R的精度范围内。对于图3(b)的中等粒径组，组次较多(共444组)，因此整体上更能反映公式精度：在2.0～3.5 m/s区间，经典起动流速公式的计算点据较为散乱，而修正公式的计算结果集中在零误差线两侧，能比较好地反映相应水流条件下卵石推移质的起动规律。流速增大时，经典公式计算值相较于实际起动流速整体偏小，而修正公式的计算结果虽然有个别点据偏大，但整体上与实测值吻合较好。

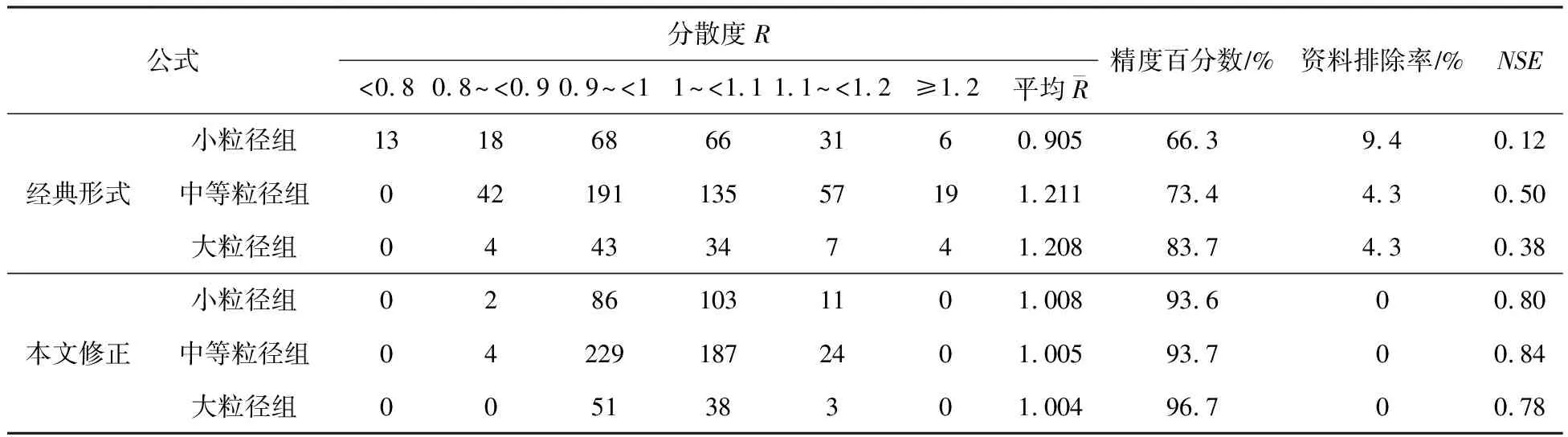
表4 各公式计算精度比较

由表4结果可看出，经典起动流速公式的分散度R值多分布在0.8～1.2区间，且随着dmax的增大，公式精度也逐步提升，但整体看来，精度百分数的平均值仅为75%。本文修正公式的分散度R值多分布在0.9～1.1区间，即R值精度范围内，精度百分数均值约为95%，资料排除率均为0。小粒径组的计算精度由原来的66.3%增大至93.6%，计算精度显著提高。

以NSE值来比较各公式精度时，结果更加直观。如表4所示，经典起动流速公式的NSE值分别为0.12、0.50和0.38，而本文修正后的NSE值分别为0.80、0.84和0.78。依据Nashi-Sutcliffe效率系数的评判标准，经典公式计算结果与实测起动流速误差相对较大，而修正后的计算精度有显著提升。综合来看，考虑粗颗粒暴露作用的修正公式在计算三堆子河段卵石推移质起动流速时能达到较好的效果。

4 三堆子河段卵石推移质输沙公式

推移质输沙率是河流动力学的基本问题之一，由于推移质本身运动的复杂性，至今还没有一个输沙率公式能全面反映卵石河床推移质输沙规律，并与不同河流实测资料吻合较好；且部分此类公式形式复杂，计算繁琐。本文分别从推移质输沙率关系与单一水流因子的建立、经典无因次推移质输沙公式结果比较、通用无因次推移质输沙公式建立三个方面，确定出适合三堆子河段的推移质输沙公式。

4.1 单一水流因子按照生产部门常用的资料整编方法，将三堆子站卵石推移质输沙率与对应的实测流量及平均流速建立如下指数形式关系：

Gs=pQq

(7)

Gs=rVs

(8)

式中：Gs为断面卵石推移质输沙率，kg/s；Q为流量，m3/s；V为断面平均流速，m/s；p、r为单一水流因素系数；q、s为指数。

根据三堆子站实测卵石推移质资料计算式(7)—(8)参数，确定拟合曲线。如图5所示，三堆子站流量、断面平均流速与卵石推移质输沙率的相关关系较差，实测点据分散，其相关系数R2分别为0.40和0.47，预测结果较差。由此可知，对于三堆子站而言，仅考虑某一水流因子对卵石推移质输沙率的影响，输沙率公式计算精度较低。

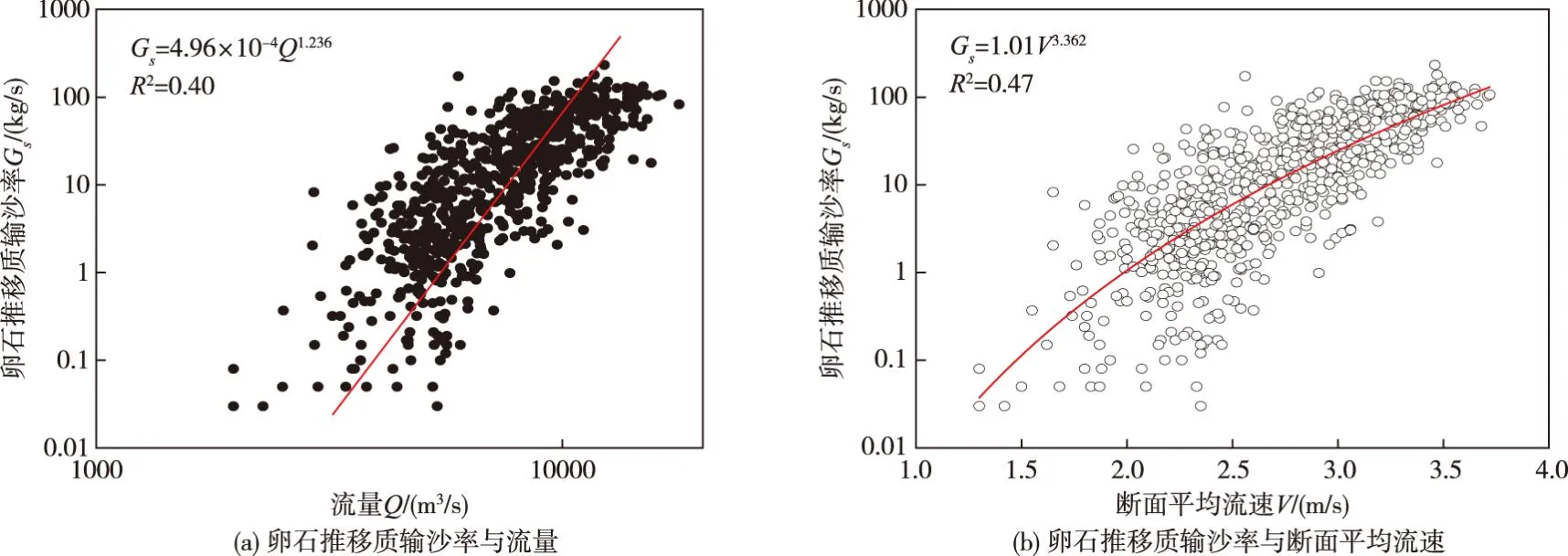
图5 卵石推移质输沙率与单一水流因素的关系

4.2 无因次经典推移质输沙公式本文选取Meyer-Peter、Engelund、Ackers-White、Tsubaki、Einstein和Yalin六个经典推移质输沙公式进行比较。为便于分析，将上述公式统一转化为水流强度Θ与输沙强度Φ的关系。其中无因次水流强度Θ和输沙强度Φ的表达式如下：

(9)

(10)

式中：d35、d50分别为泥沙累积频率分布曲线上横坐标取值为35%、50%所对应的粒径值，m；J为水面比降；gb为单宽输沙率，kg/s3。

钱宁[29]将经典推移质输沙公式统一转化为Θ与Φ的关系，上述公式转化后的形式如下：

Meyer-Peter式：

Φ=(4Θ-0.188)3/2

(11)

Engelund式：

(12)

Ackers-White式：

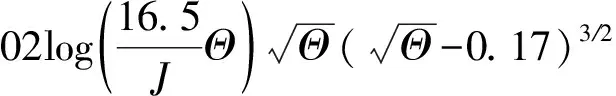
(13)

Tsubaki式：

(14)

Yalin式：

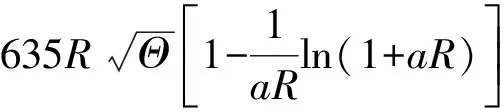
(15)

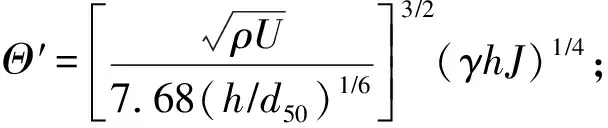
Einstein式：

(16)

(17)

式中：R′b为沙粒阻力对应的水力半径，m；A*、B*和η0根据试验资料可分别取1/0.023、1/7和0.5。

基于三堆子站实测卵石推移质资料，上述公式计算结果见图6。结果表明，除Einstein、Yalin公式外，其它公式计算结果较实测值偏大，约1～4个数量级。根据实测资料，三堆子站实际临界水流强度Θc取值大约有50%在0.06～0.12范围内，而小于0.05的仅为1%；而Meyer-Peter等公式Θc均取值0.047，远小于实际值，导致其计算结果显著偏大，尤其是在输沙强度较低时，最大可相差4个数量级；Yalin公式的临界水流强度Θc通过希尔兹曲线查得，由实测水流泥沙资料查得的结果多为一定值，即Θc=0.06，与实际临界水流强度较为接近，因而Yalin公式的计算精度较其他公式而言相对较好。

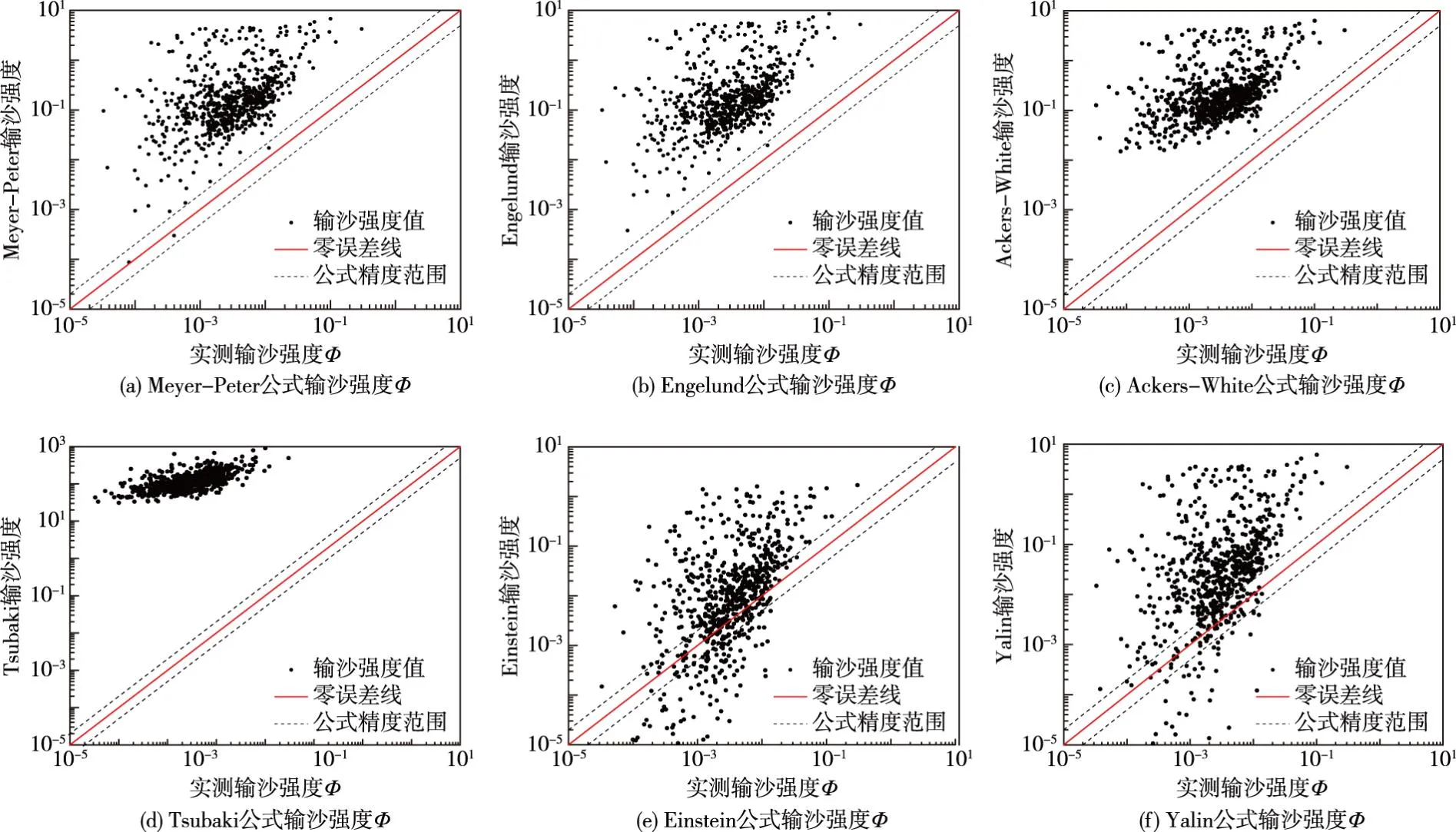
图6 各无量纲输沙强度公式结果对比

利用分散度R及NSE值对上述经典推移质输沙公式的精度定量评价。如表5所示，经典公式R值较大，且NSE值均远小于0，计算精度很差。这可能是由于三堆子河段河床多为粗颗粒卵石，颗粒间的隐暴作用显著，起动较为困难，而经典输沙公式一般是基于均匀沙水槽实验资料建立的，其不能很好地反映多种因素影响下该河段卵石推移质的输移规律，因此有必要在前人理论的基础上，根据本河段具体情况对推移质输沙公式进行修正。

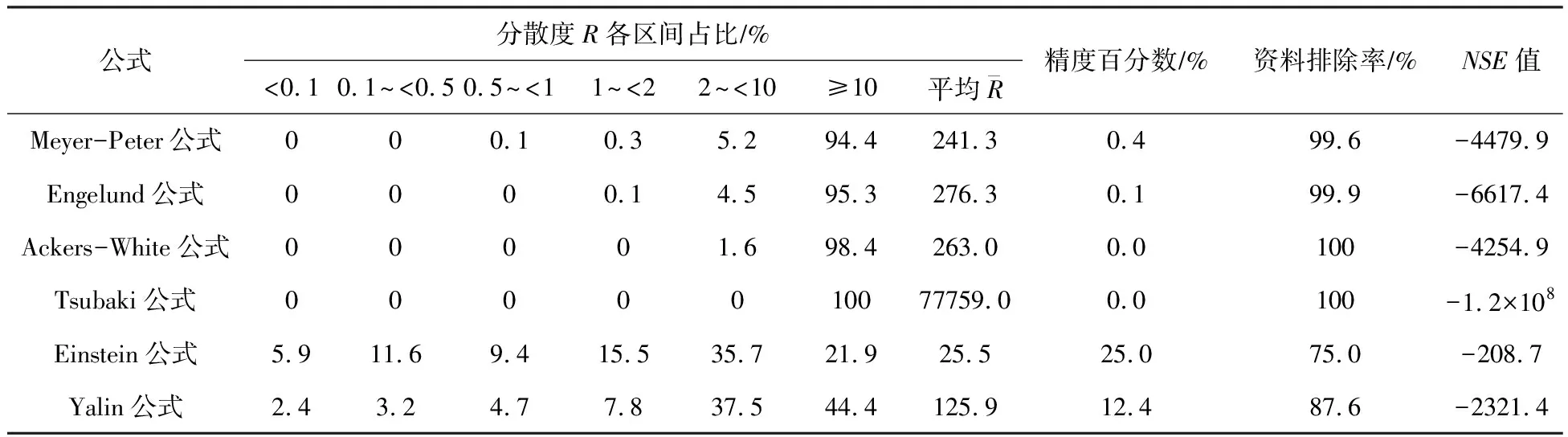
表5 各推移质输沙率公式精度比较

4.3 无因次水流强度指标水流强度大小是决定泥沙运动强度的主要因素，因此分析水流强度与输沙强度关系，关键在于水流强度指标的选取。河流中水流强度指标可以使用切应力τ=γhJ、断面平均流速U、水流功率W=τU、弗劳德数Fr等物理量表示，对各指标进行无因次化如下：

(18)

(19)

W*=τ*U*

(20)

(21)

式中τ*、U*、W*分别为无因次切应力、无因次流速和无因次功率。

利用三堆子站实测卵石推移质资料点绘上述无因次水流强度指标与输沙强度Φ的关系，如图7所示。结果表明，除Fr-Φ的关系较差外，各水流强度指标与输沙强度Φ之间具有较好的关联度，其中τ*-Φ的关系最好，这是由于泥沙运动主要与切应力有关；U*-Φ和W*-Φ的相关关系较前者为差，这是因为能量通过水流传递给床面泥沙的过程中，存在着能量消耗，且阻力系数也有一定的影响，各因素之间是复杂的多值关系，因而相关性相对较差。

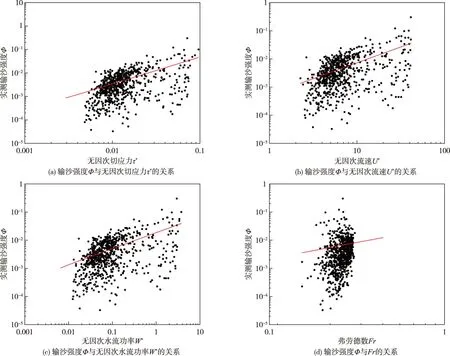
图7 输沙强度Φ与无因次水流强度的关系

整体上，各水流强度指标与输沙强度Φ之间的点据散乱，相关系数较低，有必要根据三堆子河段的水流特性，进一步优化已有公式和强度指标的结构形式、参数大小，以更好地预测输沙强度。

4.4 修正公式

4.4.1 输沙公式的无因次形式 输沙公式的本质是建立单宽输沙率gb与水流条件T之间的关系，以往学者[20，31-32]多采用如下形式：

gb=kTw

(22)

式中：k为系数；w为指数。由于水流强度与输沙强度的量纲不尽相同，且为了方便与已有的公式结果直接比较，需对二者无因次化。通过分析各类代表性卵石推移质输沙公式，明确影响水流强度的主要因素，包括平均水深h、平均流速U和水面比降J，因此水流强度指标T可表示为：

T=f(h，U，J)=k′hv1Uv2Jv3

(23)

式中：k′为系数，仅与水流和泥沙的性质有关；v1、v2、v3为指数。

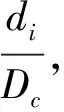
综上，无因次化后水流强度指标可表示为：

(24)

式中：T*为水流强度指标T的无因次化形式；k″、l1、l2、l3、l4、l5为常数。

无因次单宽输沙率仍采用上文的输沙强度Φ，则输沙公式的无因次形式可表示如下：

(25)

式中m1、m2、m3、m4、m5、m6均为待定系数。

4.4.2 输沙公式的率定 基于三堆子站卵石推移质实测资料，通过多元回归分析确定式(25)中的各项参数。率定后的输沙率公式如下：

(26)

化简后得：

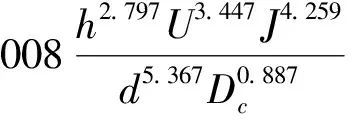
(27)

利用上述修正公式计算三堆子站的卵石推移质输沙率，并与实测值进行比较，如图8所示。

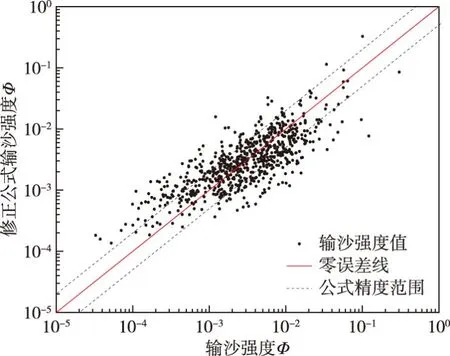
图8 修正公式值与实测输沙率的关系

由图8可见，本文修正的输沙率公式与实测值相关关系较好：在实测输沙强度小于10-4时，计算值略有偏大，但最大偏大1个数量级左右；随着输沙率的增大，在Φ=10-4之后计算值均匀地分布在零误差线两侧，且位于公式计算精度区间的点据相较于经典输沙率公式明显增多。考虑到实测卵石推移质输沙率具有较大的脉动性，例如相同的水流条件下，实测卵石推移质输沙率亦有可能相差1～2个数量级，因此修正公式的计算结果可以认为是合理的。

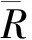
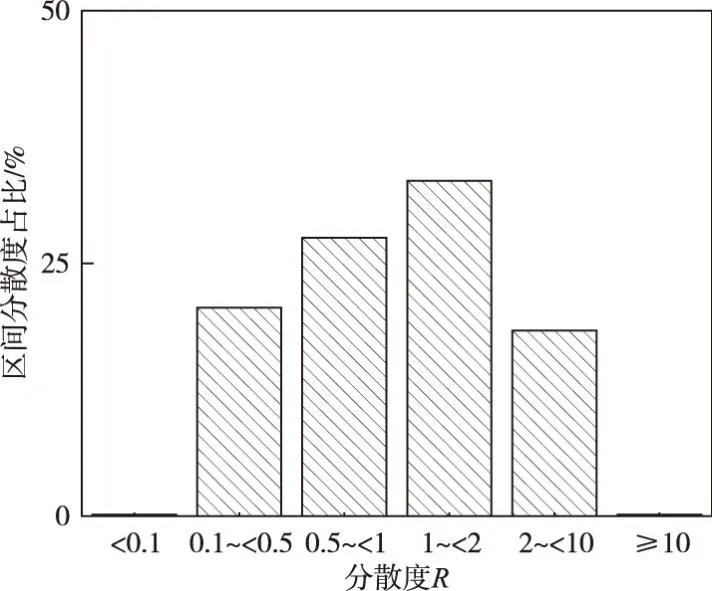
图9 分散度R分布区间

5 结论

基于三堆子站2008—2021年实测水沙资料，分析了金沙江下游卵石推移质的起动及输移规律，比较了经典泥沙起动流速公式及推移质输沙公式，并针对产生误差的原因对公式予以修正。结论如下：

(1)金沙江上中游梯级水电站投产运行后，金沙江下游干流入库径流量未发生趋势性变化，但水库的拦洪削峰作用改变了径流过程，使得较大流量出现的频率减小；2013—2021年多年平均悬移质输沙量和卵石推移量相较于2008—2012年均显著减少，减幅分别为73.6%和32.1%，对应时段的卵石推移量占总输沙量的比例由0.6%增大至1.5%，在金沙江下游入库泥沙中的比重加大。

(2)针对以往泥沙起动流速公式中综合系数K取为常数的做法，建立了K值与最大粒径dmax的关系，以表征非均匀沙粗颗粒暴露作用等因素对卵石颗粒起动的影响。基于实测资料，分别得到了小粒径组、中等粒径组和大粒径组卵石推移质起动流速修正公式，其计算结果与实测起动流速吻合较好，精度百分数约为95%，资料排除率为0，NSE值均在0.78以上。