基于预探索的动态自适应3DVFH+无人机避障算法

何晨阳，王耀力，常 青，孙永明

（1.太原理工大学信息与计算机学院，山西太原 030024；2.山西省林业与草原科学研究院，山西 太原 030024）

旋翼无人机广泛应用在农业[1]、消防[2]、电力检测[3]等诸多领域。因此，对于无人机来说，能够在未知且复杂的环境下实现高效感知复杂环境下自主规划航迹并实时规避障碍物至关重要[4]。

无人机的避障规划算法可分为全局避障规划算法和局部规划算法，全局规划算法需要对环境进行建图并将环境信息存储起来，在已知环境地图的前提下进行规划[5-6]。全局规划算法包括Dijkstra 算法[7]、A*算法[8]、Hybird A*算法[9]、Lazy Theat*算法[10]、D*算法[11]以及RRT（快速拓展随机树）算法[12]等，该类算法不会陷入局部最优的问题，但需要消耗大量内存来存储环境信息；局部规划算法对环境信息不做存储，实时生成避障指令，比如人工势场法[13]、BUG 算法[14]、DWA（动态窗口）算法[15]、VFH（静态矢量场）算法[16]以及3DVFH+算法[17]等，该类算法不需要存储环境信息，所需内存资源非常小，但会陷入局部最优解。综合对比以上各类算法，结合旋翼无人机平台硬件资源稀缺且作业区域是三维环境，决定采用3DVFH+算法作为研究对象，针对该算法存在的问题作出改进。

文中将3DVFH+作为一个纯局部算法，不需要构建全局地图。全局地图被3D 点云所取代，开发一种成本较低的3D 环境避障算法。

1 避障规划算法

3DVFH+算法利用Octomap 框架来表征环境信息，以octotree（八叉树）的形式构建全局地图，从全局地图中提取环境信息，生成障碍物直方图进行避障。

1.1 环境建图

Octomap 数据结构是一种表示3D 环境的有效方法[18]。八叉树中的每个节点表示包含在立方体的空间，通常称为体素。如图1 所示，白色叶子节点为空闲状态，灰色叶子节点状态为占据状态。通过这种方式，将整个环境都由体素进行表示。

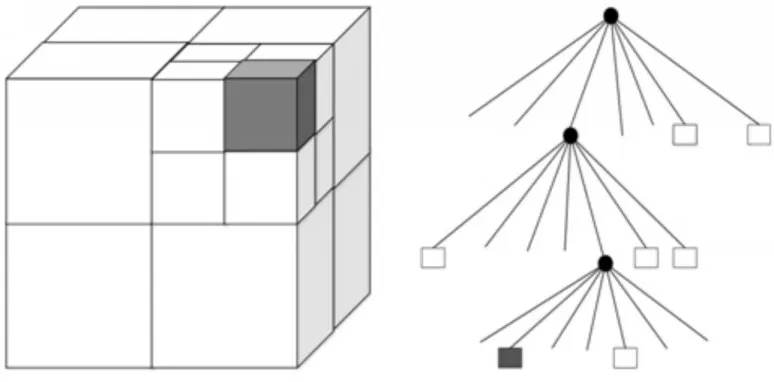
图1 八叉树结构

在对环境的观测过程中，往往会受到噪声或者是环境本身动态特性的影响，导致节点是否被占据属于概率事件。假设t=1,2,…,T时刻，观测到的数据为z1,z2,…,zT，则第n个节点被占据的概率为：

对式(1)进行logit变换，将概率变换至全实数空间：

反变换为：

式中，α称为log-odds，用L() 表示节点的logodds，则上式变为：

由此将空间点状态的概率问题转化成对实数空间的加和运算。

1.2 3DVHF+算法

1.2.1 算法原理

3DVFH+算法一共分为四个阶段，用于计算无人机下一时刻的航路点。

1）八叉树地图探索

当无人机在大型环境中移动时，由于计算能力的限制，不可能探索所有的体素，因此，八叉树探索阶段只研究无人机周围包围框内的体素。包围框以无人机中心点为中心，大小为ws·ws·ws。

2）构建2D 主极直方图

将三维体素映射到二维主直方图中，二维主极直方图的横坐标为方位角，纵坐标为俯仰角。对于三维点云中的每个点云数据，计算无人机位置相对于该点云的方位角θz和俯仰角θe，然后将该点映射到二维主极直方图中。

如图2所示，在笛卡尔坐标系下对体素进行建模。

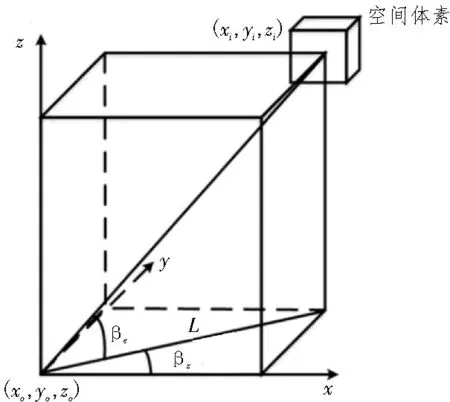
图2 体素在笛卡尔坐标系下的表示

图2 中，(xo,yo,zo)为无人机的质心坐标，(xi,yi,zi)为障碍物体素的坐标，则有：

其中，L可表示为:

3）二值化极直方图

将2D 主极直方图中的每个格点的值与两个阈值τlow和τhigh进行比较，大于τhigh时，将该格点置为1；小于τlow时，将该格点置为0。如果格点的值位于两个阈值之间，则用该格点旁边的值来替代，如式（8）所示，这两个阈值允许算法区分真实障碍物和测量误差。

4）路径检测与选择

为了确定可用路径，使用滑动窗口在2D 主极直方图中进行检测，如果窗口中的所有元素都等于0，则将该窗口标记为可通过，这样可以得到所有的候选方向，然后计算代价函数得到最优方向。

3DVFH+算法同时将候选方向与目标方向、当前方向、前一时刻方向的差值考虑进来。采用式(9)所示代价函数得到最佳的前进方向：

式中，dk为第k个候选方向，Δ 为计算两项的绝对值，λ1、λ2、λ3分别为各个代价项的权重因子。第一项表示dk与目标方向kt的绝对差值，第二项表示dk与无人机航向角的绝对差值，第三项表示dk与无人机上一时刻运动方向kd,n-1的绝对差值。

1.2.2 3DVFH+算法仿真

使用四轴旋翼飞行器作为实验平台，通过设置“倒L”型以及长墙障碍物来说明算法的局部死区以及最优解问题。

如图3 所示，对于长墙障碍物，无人机在障碍物面前往返飞行，犹豫不定。对于“倒L”型障碍物，无人机在拐角处往返飞行，陷入局部死区。同时可以看出，针对“倒L”型障碍物，由于视野正前方没有障碍物，故无人机选择了一条更长的路径，暴露了算法局部最优问题。

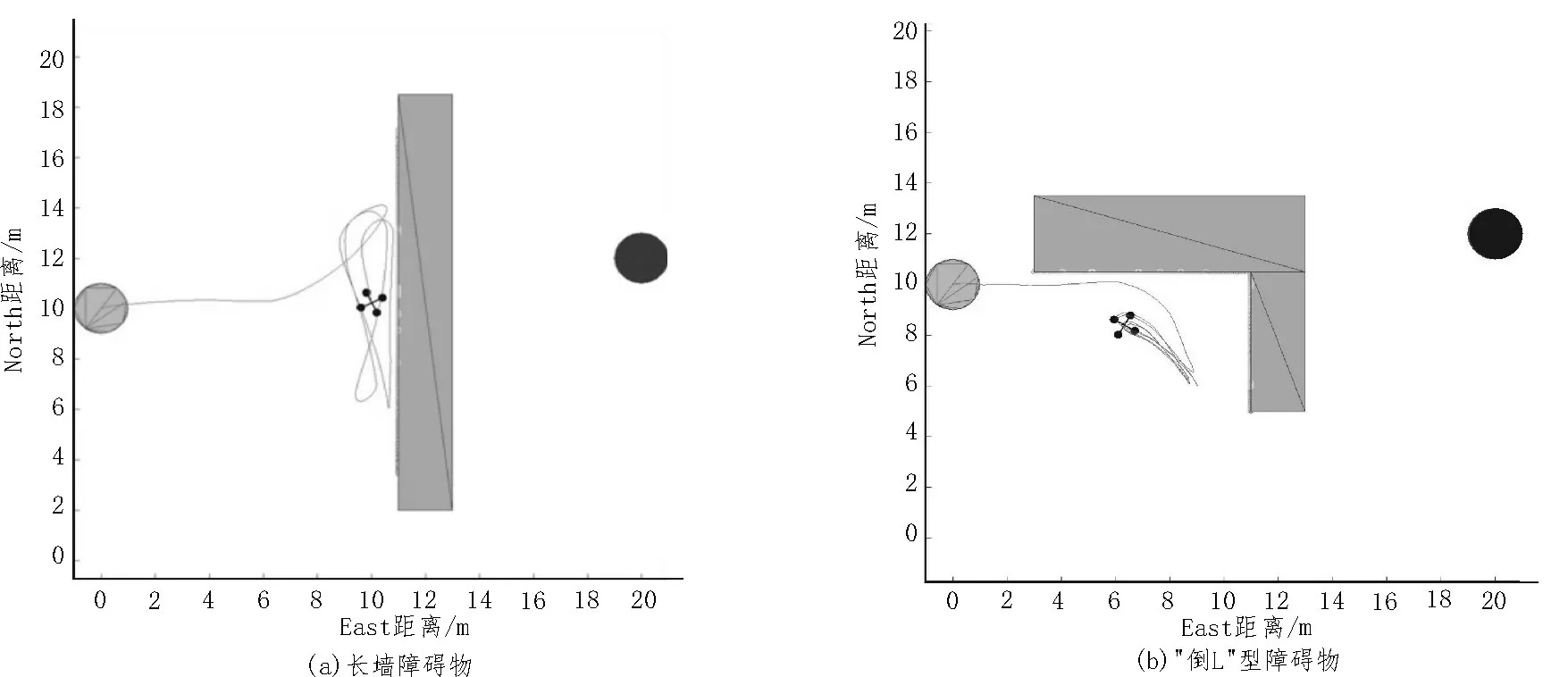
图3 原生算法

2 基于预探索的动态自适应3DVFH+算法

3DVFH+算法无法根据环境特性实时动态地做出调整，导致在面对特殊障碍物时会陷入局部死区。同时3DVFH+作为一个纯局部算法，存在局部最优解的固有问题。下面将对这两个问题进行改进。

2.1 自适应代价函数

在原生代价函数中，当候选航路点与目标点之间的距离到达某一阈值时，代价由候选航路点与目标之间的距离主导，此时无人机便会做出转向的决策，从而造成了无人机往返飞行犹豫不定的现象。

对于3DVFH+算法的局部死区问题，根据飞行进度对代价函数的目标距离权重因子进行动态调整，设置自适应代价函数来消除算法的局部死区问题。

首先将原始代价函数分为两部分，分别是导航方向代价和路径平滑代价，如下所示：

将代价函数式（10）细化为偏航代价与俯仰代价两部分，如下所示：

f(dk)t为导航方向代价，分为偏航代价和俯仰代价两部分，对应的权重因子分别为λt_yaw和λt_pitch值。总的代价函数如式（13）所示：

其中，参数kt为导航方向代价的权重因子，参数ks为路径平滑代价的权重因子。可通过配置上述各个代价项的权重因子得到侧重性能不同的算法效果。

为实现对飞行进展进行监控，动态调整无人机距离目标的成本，需要监控无人机与目标距离的趋势。文中采用滑动平均滤波器来表征无人机行为，如式（14）所示：

式中，t[k] 为当前时刻，d[k] 为当前时刻无人机与目标之间的距离。当s[k] 为负值且绝对值较大时，说明无人机飞行效果良好，在不断靠近目标点；当s[k] 在零附近时，说明无人机在沿着障碍物做长时间的绕行；当s[k] 为正值且较大时，说明无人机在不断地远离目标点。

有了对飞行行为的表征后，先为权重因子λt_yaw设定一个最大值λt_yaw_max和最小值λt_yaw_min以保障飞行安全。引入斜率阈值st且为负值，当s[k] 小于st时，说明此时无人机正在接近目标，不用调整；当s[k] 大于st且在零值附近时，引入区间Δsec来衡量s[k] 与零的绝对差值，说明无人机正在做无用的绕行，需要对绕行动作加以抑制，故以一定的速率rdec减小λtarget_yaw；当s[k] 大于st且为正值时，说明无人机正在远离目标，若在无人机视野范围FOV 内检测到障碍物，则以一定的速率rdec减小λt_yaw，允许无人机为了避开障碍物而做出适度远离目标的行为，若在FOV 内没有检测到障碍物，则以一定的速率rinc增大λt_yaw，即在没有障碍物情况下增大无人机远离目标的代价，使无人机更快到达目标，如式（15）所示：

对采用自适应代价函数的3DVFH+算法在同样的障碍物环境下进行仿真，结果如图4 所示，可以看出改进之后的算法消除了原生算法的局部死区问题。

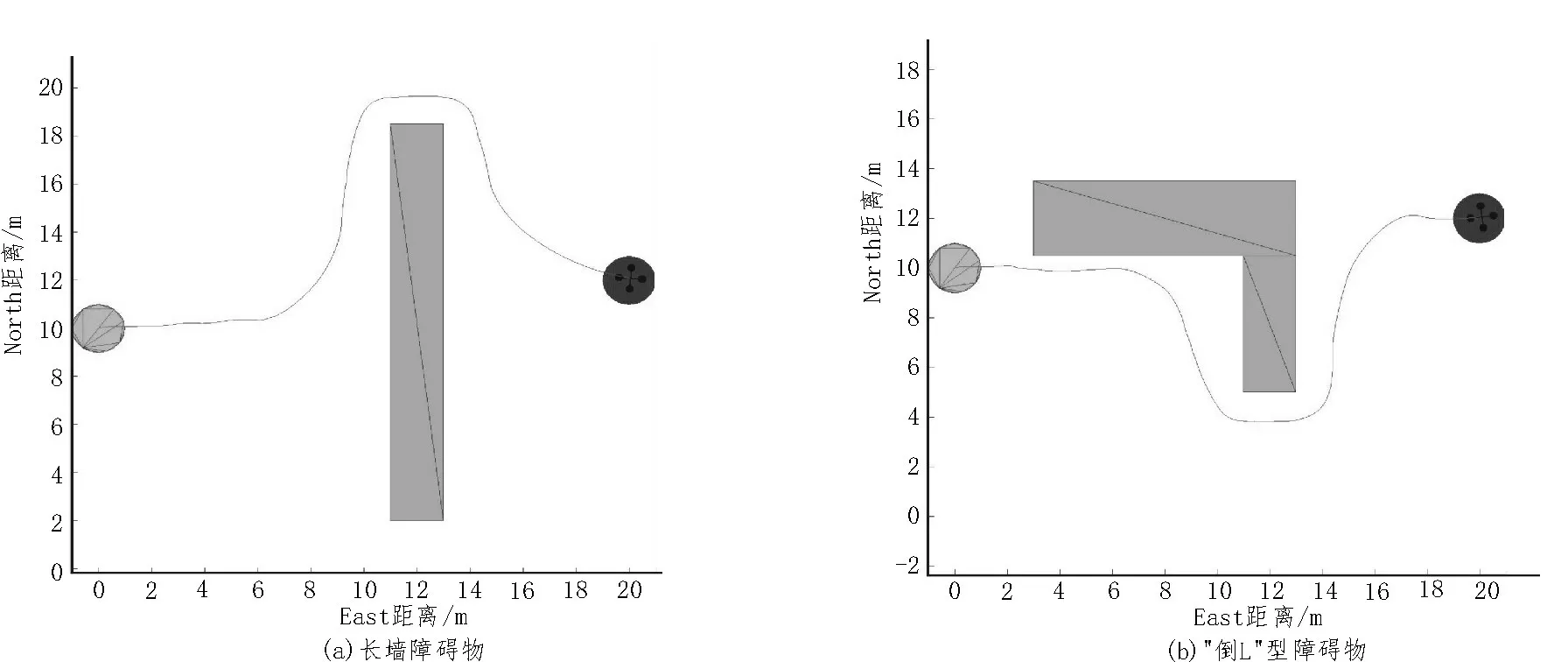
图4 改进算法

2.2 预探索机制

通过图4(b)可以看出，自适应代价函数解决了算法的局部死区问题，但无人机当前规划的航迹并不是最优轨迹。文中提出了预探索机制，通过构建搜索树消除局部最优的缺陷。

如图5 所示，虚线为无人机所有的探索节点，实线为代价函数值最小的节点方向。O点为无人机当前位置，Ai、Bi、Ci、Di、Ei为无人机未来可能到达的位置。从所有的候选方向中计算出代价最小的方向，在此方向上前进ds继续进行探索，经过N次直方图的迭代并逐步构建搜索树，树的根节点为O，深度为Dtree。当树深度为1时该算法便退化为原生3DVHF+算法。

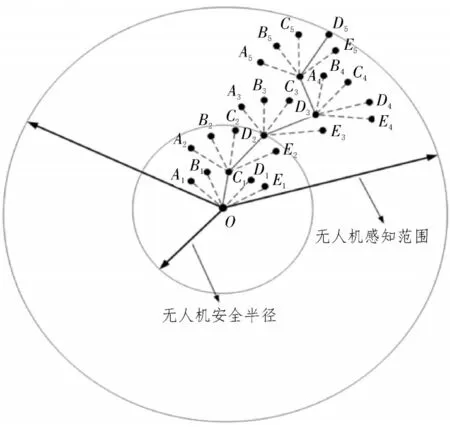
图5 预探索

如图6 所示，建立预探索后的算法对整个传感器范围进行探索，消除了原生算法局部最优的问题。

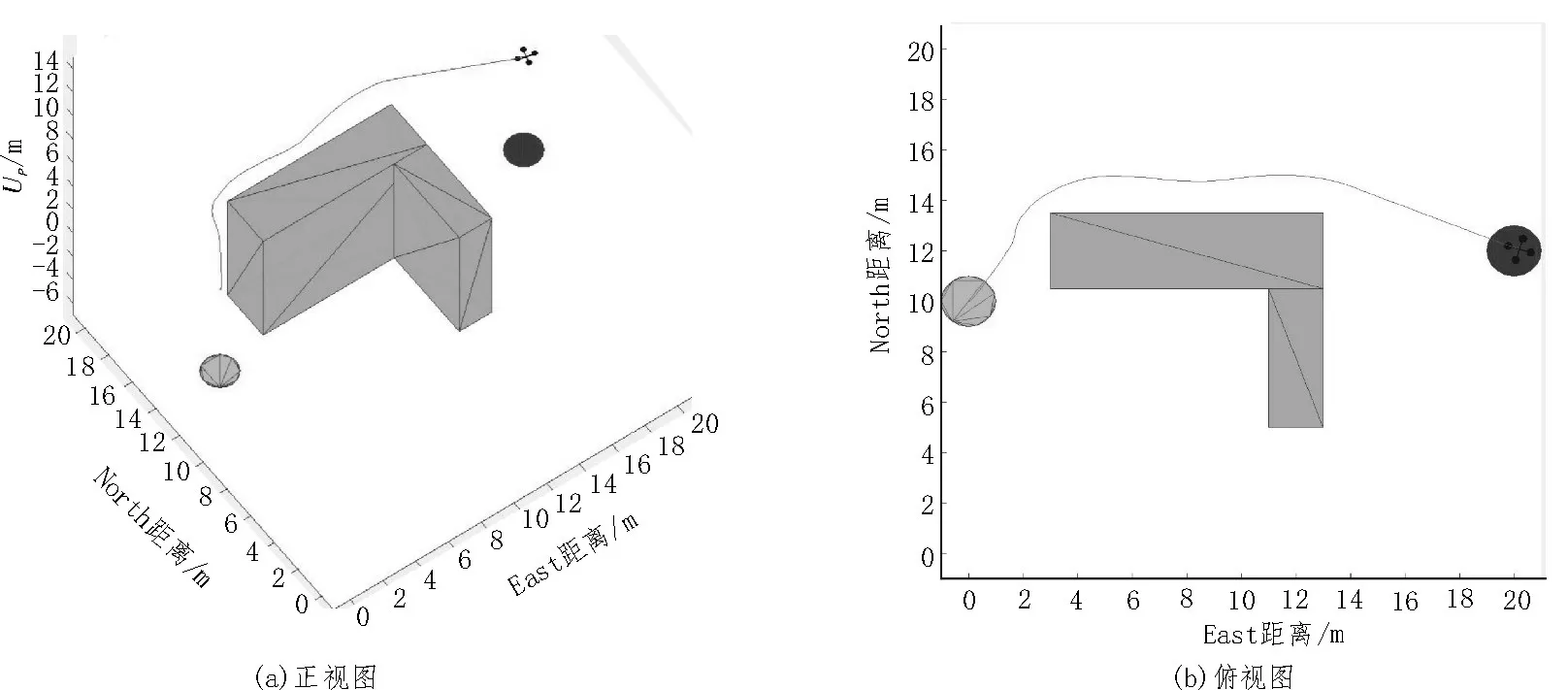
图6 消除局部最优

3 3D可视化仿真平台算法验证分析

3.1 仿真平台搭建

如图7 所示，PX4 飞行控制器是无人机的控制核心，该模型上搭载了一个深度相机，提供点云数据。仿真引擎Gazebo模拟无人机及外部环境，它允许在无人机模型上搭载传感器，以提供数据输出流，模拟真实环境。机载计算机提供ROS操作系统运行环境。

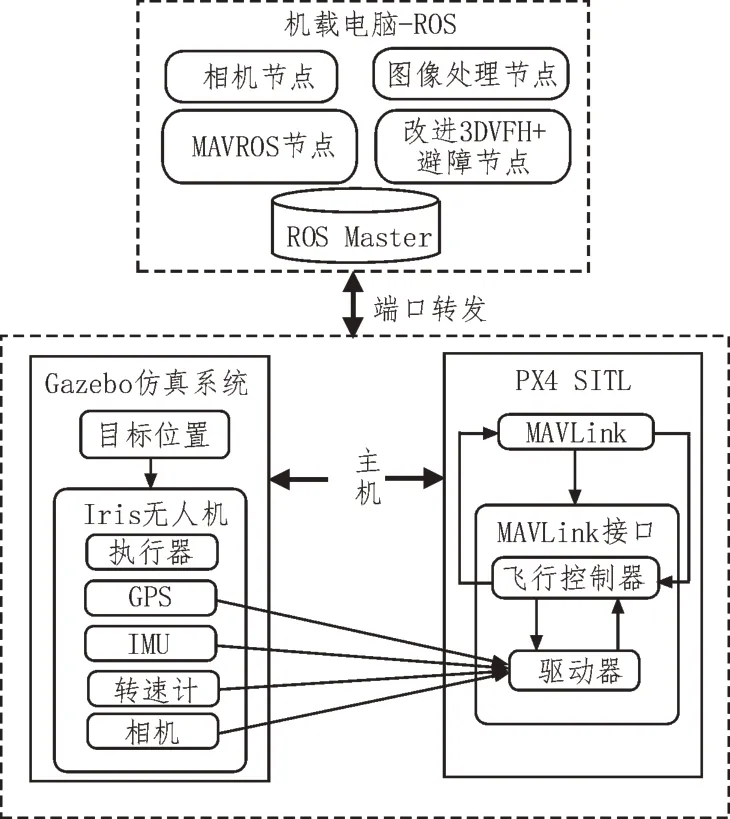
图7 仿真系统架构

3.2 仿真结果

设置无人机与障碍物之间安全距离为2 m。改进算法与原生算法对比如图8 所示。实线为预规划轨迹，虚线为预规划轨迹经过飞行控制器结合无人机动力学特性后的实际飞行轨迹。

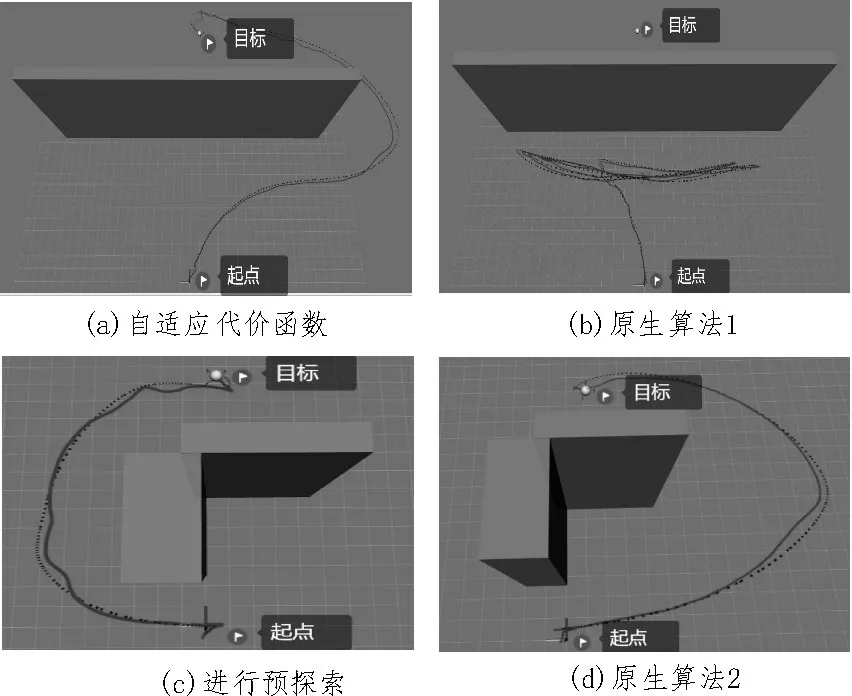
图8 改进算法与原生算法对比

如图8(a)、(b)所示，针对原生算法的局部死区问题，设置长墙障碍物，目标点坐标为(12,0,3)，无人机起点坐标为(0,0,0)，长墙障碍物中心点坐标为(8,0,6)，尺寸为(1,30,10)。原生算法陷入局部死区，而改进算法顺利到达目标点。如图8(c)、(d)所示，针对原生算法局部最优问题，同样设置“倒L”型障碍物。目标坐标为(20,0,3)，起点坐标为(0,0,0)，水平方向障碍物中心坐标为(7,-2,5)，尺寸为(1,5,10)。垂直方向障碍物中心坐标为(5,1,5)，尺寸为(5,2,10)。在算法构建搜索树的决策中，对“倒L”型障碍物下方空间。也进行了探索，当探索到障碍物时便停止了探索，并通过对上方空间的探索找到了更优路径。

表1 是算法在面对不同类型障碍物的规划路径长度和时间对比。对于长墙障碍物，原生算法陷入死区，而改进算法消除了死区现象，成功到达目标点；对于“倒L”型障碍物，改进算法解决了局部最优解问题，相较于原生算法规划航线缩短了37.15%，时间减少了25.87%。

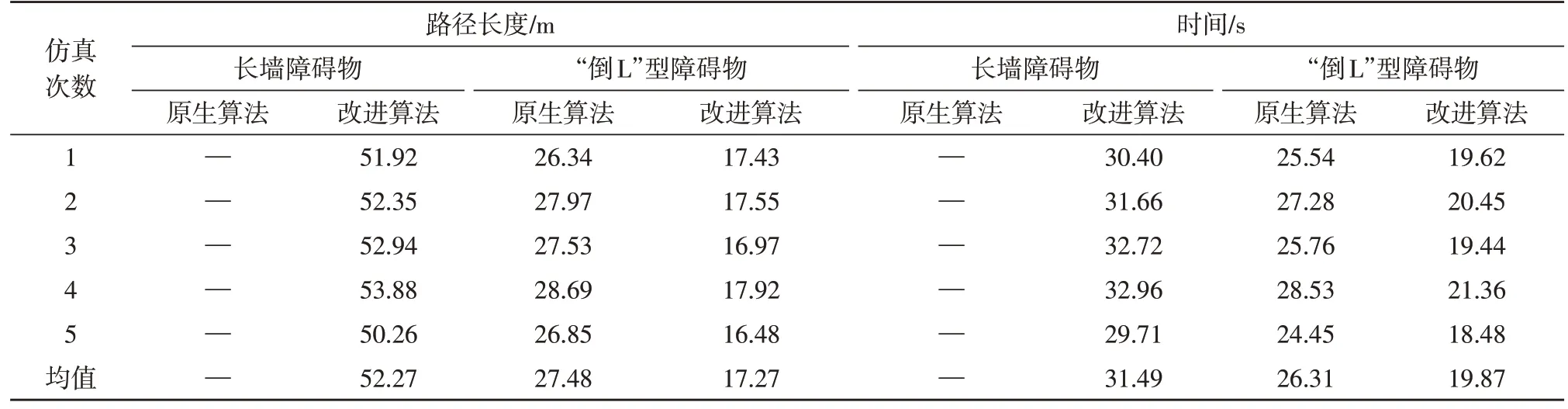
表1 算法效果对比表

3.3 航迹规划

森林相对来说环境复杂度较高，点云稀疏且不规则，无人机在森林环境避障的难度较大。如图9所示，搭建森林模型，利用地面站规划航迹上传至飞控，共设置了七个航路点，可以直观地看出无人机进行自主避障生成的平滑且无碰撞的飞行轨迹，进一步验证了改进算法的有效性。

图9 森林障碍物轨迹规划

图10 所示是所提算法与使用八叉树框架进行建图的3DVFH+算法在执行相同飞行任务时的所需资源对比，横坐标为飞行时间，纵坐标为所占资源比例。可以看出，改进算法由于不用进行建图和存储环境信息，RAM 节省了约25.26%。

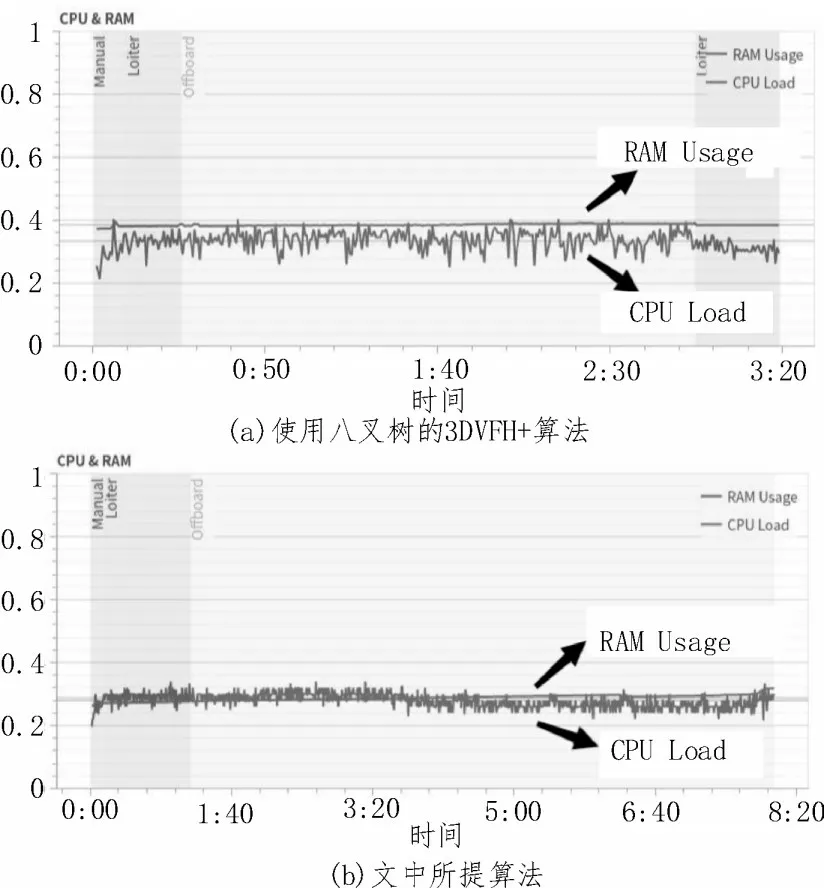
图10 CPU和RAM使用情况

4 结束语

文中提出了一种基于预探索机制的动态自适应3DVFH+避障规划算法，该算法作为一个纯反应式的避障算法，不需要对环境建图且不存储环境信息，减小了对存储资源的消耗。实验表明该文提出的避障规划算法在面对特殊复杂障碍物时仍能生成一条平滑无碰撞的飞行轨迹，生成的路径长度更短，所需时间更少，且不会陷入死区和局部最优解问题。