基于极限学习机的超短期电力负荷度量研究

何大可，荣功立，姚岱州，马浩原，史 爽

（1.成都信息工程大学自动化学院，四川成都 610095；2.国网四川省营销服务中心，四川成都 610046）

精确度量短时负荷可以保证机组的经济、合理启停，确保电力系统的安全和稳定，从而为发电公司带来更大的经济效益和社会效益。在综合度量模式的基础上，采用相似日的负荷数据可以显著地改善度量的准确性。由于各区域、各时期的负荷变化规律不尽相同，因此，在选取相似日时，要结合具体的情况，按区域、时段选用相应的计算方式。文献[1]提出了基于模拟退火算法优化深度置信网络（Simulated Annealing-Deep Belief Network,SA-DBN）的度量方法。首先利用集合经验模态分解算法（Ensemble Empirical Mode Decomposition，EEMD）对原数据进行分析，然后利用SA 对DBN 中各个隐藏层的节点进行优化，再利用SA-DBN 模型对重建后的数据进行单独度量，并将各个序列的度量结果进行迭代处理，从而得出最后的度量曲线；文献[2]提出了基于聚类经验模态分解的度量方法。该方法首先采用基于经验模式的模态法分解负载，然后利用k平均聚类法分类了各个成分，并从中选择最好的分类标记来构建神经网络的输入，最后每一组数据都被单独地导入到一个混合神经网络中，由卷积神经网络（Convolutional Neural Networks,CNN）从不同的数据之间发现不同的特点，构成一个特征矢量，然后把这些特征输入到长短期记忆网络(Long Short Term Memory networks,LSTM)中进行度量。由于电力系统负荷与天气、经济、假期等诸多方面有着紧密联系，且其变化规律是随机的，造成负荷度量精度有待进一步优化。针对该问题，文章提出基于极限学习机的超短期电力负荷度量方法。

1 极限学习机下的冗余数据消除

超短期电力负荷度量是在综合了电力系统运行特性、容量决策、自然条件和社会因素等条件下，运用一种系统的计算手段，对历史和未来的负荷进行系统地计算，以达到某种精确度的目的[3]。由于负荷因素具有较强的非线性和较强的冗余性，因此常规的算法不能有效地去除数据间的冗余度和较大的非线性特性，而这正是导致负荷度量不精准的关键因素[4-5]。

极限学习机用来训练隐藏层前馈神经网络[6]，与传统训练算法不同，极限学习机选取输入层权重，输出层权重则通过最小化正则项构成损失函数。当得到所有网络节点权值后训练极限学习机，通过输出层权重就可计算出网络输出完成对超短期电力负荷数据的度量，极限学习机的网络结构如图1 所示。

图1 极限学习机网络结构

在相同的条件下，相同时间内、相同载荷特性曲线的演变趋势比较接近，所以在相似日利用相似时段的负荷数据来进行度量，可以很好地把握电力系统的负荷动态，进而精确地测量出电力系统的负荷[7-9]。由于每个子模式的输入矩阵都是随机选择的，所以虽然是同一个输入，但得到的自适应性结果不同，而且每个子模式的输出也有很大的差异[10]。因此，若将各个子模式的输出算数关系值当作其输出，则无法很好地分辨各个子类的优缺点，故选用较小的权重，反之，则选用较大的权重，这样就能充分地展现出各个子模式的优越性[11-12]。为了使电力负荷度量偏差较小，应使子模式具备较大的权重，公式为：

式中，n表示输出总次数；M表示子模式输出个数；表示第M个子模式输出的偏差；i表示输出次数。通过式（1）对误差较小的子模式赋予一个较大的权重，而对误差较大的子模式赋予一个较小的权重，从而消除了冗余数据。

2 超短期电力负荷度量

极限学习机网络结构类似于单隐藏层神经网络[13]，只是在训练阶段需要输入随机输入层的权值和偏差，方便后续训练，此时实验数据利用求取的输出层权重便可输出电力负荷度量结果。以负荷为模型输出，以负荷影响因素为模型输入，以极限学习机的方法计算超短期电力负荷度量，其主要步骤为：

步骤一：在相似性原则下[14]，相似日同期的负荷曲线没有明显的改变，而近期相同类型的相同时间段，其负荷的变动趋势也比较接近，所以采用相似日数据进行负荷度量可以有效地改善度量的准确性。因此需要准确读取历史负荷、节日和天气等相关的输入数据；

步骤二：将极限学习机网络视为一个函数，该结构隐藏层输出结果可表示为：

式中，h1(x),h2(x),…,hn(x)为隐藏层样本集。式（2）的输出结果不是唯一的，不同输出函数可用于不同的隐藏层神经元。该神经元由隐藏层节点参数组成的，满足通用逼近能力定理，是一种非线性分段连续函数[15]，结合激活Sigmoid 函数表示为：

式中，ex表示偏差。利用式（3）标准化处理样本数据，并平滑处理采样数据[16]。数据经过隐层进入输出层，以获取隐藏层神经网络的输出结果。

步骤三：统计样本数据的主要成分，并构造一组训练样本、一组度量样本和一组主成分样本；

步骤四：设置最大隐藏层节点数目和切换准则，将建立的多个神经网络子模式分为误差较小的更新子模式和保持子模式，使模式输出波动性达到最小。设第t个时刻得到的样本数据切换准则为：

式中，λ用来判断各个子模式权重计算结果是否在控制范围内。如果大于设定的阈值，需要更新子模式，采用随机赋值方法重新赋值，减小训练误差；如果小于等于设定的阈值，需要保持子模式，采用随机方式更新，减小输出结果波动性[17]。

保持子模式状态下根据式（5）输出计算结果：

更新子模式状态下根据式（6）输出计算结果：

式中，βi表示偏差较小情况下的神经网络较大权重。一旦有新的输入数据输入时，需根据切换准则对子模型进行判断，进而获取总输出结果。

步骤五：确定最优的数据组，包含了训练样本量、检测样本量、隐含层输出量和输出权值；

步骤六：多次采样训练网络，当出现新的数据时，再依据切换准则做出决策。

重复上述步骤，获取极限学习机的度量结果。

在超短期负荷度量中，由于数据之间的间隔都很短，所以在该区间内，大气、气温等参数对度量结果没有任何影响。经过规范化运算，获取超短期各个电压序列间的相关关系，并剔除不可靠数据，进而得到如下电力负荷度量输出序列，可表示为：

式中，q1、q2、q3分别表示零序电力负荷、越限电力负荷、过载电力负荷。通过极限学习机映射电力系统中的负荷情况，使得相同负荷映射点映射到同一位置，由此完成电力负荷度量。

3 实验与分析

3.1 实验平台

为了获取精准电力负荷，构建图2 所示的实验平台，分析负荷使用情况。

图2 实验平台结构

通过设置若干电力负荷计算单元，分析各个节点电力负荷情况，并统一发送给对应的边缘计算服务器。结合电力负荷计算单元实时监测的负荷情况进行度量。

3.2 实验数据及实验流程

以2022 年12 月21 日、12 月25 日17:30 到23:30的电力负荷数值为实验数据，对该区域的超短期负荷进行了实验分析，如图3 所示。

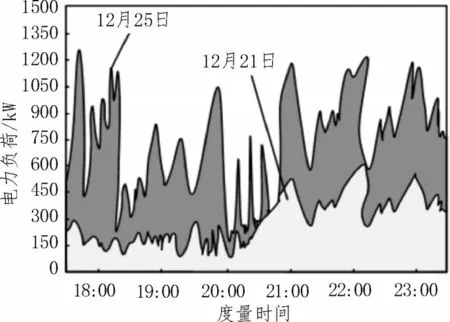
图3 超短期负荷的实验分析

由图3可知，12月21日电力负荷的波动范围为0～600 kW；12月25日电力负荷的波动范围为0～1 280 kW。在负荷度量时，由于人为因素或者机器的原因，导致数据出现误差、丢失、突变等情况，对度量的准确性产生不利影响。为此，统一实验测试步骤如下：

步骤1：平滑处理并校正实测负荷数据，得到较为精确的输入采样值；

步骤2：为防止在训练时出现数据饱和问题，剔除所有的参量，并对所有的输入数据进行标准化处理，以保证所有的采样值均在0 到1 的范围内，从而提高实验速度；

步骤3：确定实验指标：选用均方根误差作为评价指标，公式为：

式中，m表示计算次数；yi、分别表示实际输出和预先设定的输出Q3的结果。式（8）结果越大，说明度量结果越不精准，反之，则越精准。

步骤4：分别使用基于极限学习机的度量方法和基于SA-DBN 的度量方法、基于聚类经验模态分解的度量方法对预处理后的负荷实测数据进行测试，并输出实验结果。

3.3 实验结果

使用三种方法对比分析12 月21 日、12 月25 日电力负荷是否与实测数据一致，如果一致，则说明度量结果精准，如图4 所示。

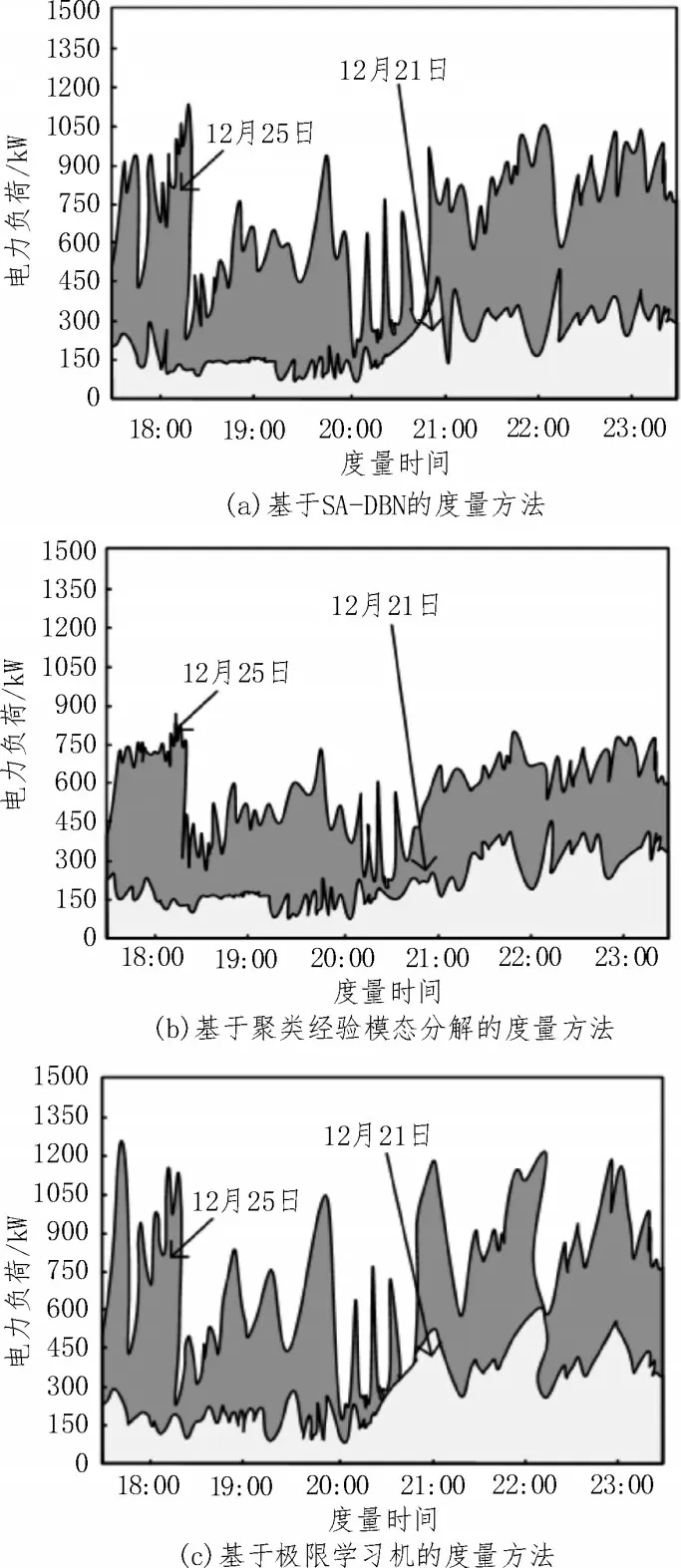
图4 不同方法度量结果对比分析

由图4 可知，采用基于SA-DBN 的度量方法、基于聚类经验模态分解的度量方法与图3 所示度量结果不一致；采用基于极限学习机的度量方法与图3所示度量结果一致。所提方法12 月21 日电力负荷的波动范围为0～600 kW；12 月25 日电力负荷的波动范围为0～1 300 kW，与图3 数据存在较小的误差。

4 结束语

通过引入极限学习机可以提高超短期电力度量精度，该文根据切换准则，将建立的多个神经网络子模式分为误差较小的保持子模式和更新子模式两部分，进而减小不同模式下输出的波动性，使得度量误差达到最小。