跨海桥梁基础波浪力断面对比与研究

崔苗苗，毕昕宇，李 鑫，祝 兵

(1.中铁第四勘察设计院集团有限公司,武汉 430063; 2.西南交通大学土木工程学院,成都 610031)

近年来,随着经济的快速发展以及“21世纪海上丝绸之路”和“一带一路”倡议的提出和逐步实施,我国已建成了东海大桥、青岛海湾大桥、杭州湾跨海大桥以及港珠澳大桥等诸多跨海大桥,而在入海口和海岸线上,更多的跨海桥梁也在修建和规划当中[1]。可以确定的是,作为沟通不同地区之间政治、经济的纽带,跨海桥梁的建设与发展在我国海洋工程中起到重要作用。墩柱、承台等基础是跨海大桥得以建设的关键所在,然而跨海大桥所处的复杂海洋坏境会给基础施工带来重大挑战,其中尤以波浪作用为甚。例如平潭海峡大桥在吊箱围堰的施工过程中,受台风“杜鹃”过境的影响,周围海域浪高达到6 m,其波浪荷载对施工产生重大影响[2-3]。同样的情况也出现在苏通大桥基础施工过程中[4]。桥梁基础在波浪力作用下的施工安全关乎桥梁基础建设的稳定性,需要给予足够重视[5]。

桥梁基础尺寸与特征波长相比属于大尺度结构物,对于这类结构的波浪力计算,我国的规范中只是针对圆形墩柱结构给出了基于绕射理论的一次近似解析解。而对矩形墩柱,则给出了经验计算方法或等效为圆形墩柱的计算方法[6]。这种计算方法对于实际工程中存在的圆端形、哑铃形、多边形等复杂结构形式的基础波浪荷载无法做到准确计算。目前对于基础结构波浪力作用的计算和研究,主要有数值模拟和物理模型试验两种方法。数值模拟方法随计算机的快速发展而逐步兴起,相比物理模型具有模拟速度快、消耗成本低、可得到数据更为全面的特点,且可以对目标结构和目标工况进行完整的足尺模拟,避免缩尺效应的影响。不少学者基于数值仿真技术对桥梁下部大尺度结构的波浪作用开展研究。祝兵[7-8]和康啊真[9]采用水槽试验和数值方法建立了三维波浪与大尺寸圆柱结构物相互作用的数学模型,结果发现圆柱波浪力、力矩的数值计算结果与试验结果和理论解吻合,建立的三维数学模型能够很好地模拟结构物所受的波浪力及力矩。LIN[10]和KANG[11]以数值仿真为基础,模拟了方柱受波浪力作用,并进一步分析了波浪作用于结构物时的绕流现象。董伟良等[12-13]基于数值模拟软件建立了三维数值水槽,进行大尺寸承台在波浪冲击下的数值分析,得出波高、淹没系数、周期以及承台长度对承台所受波浪力的影响。梅大鹏[14]在矩形结构波浪力作用的物理模型实验研究基础上,提出了大尺度矩形结构波浪力的简化算法。张胡[15]基于线性波浪绕射理论对大尺度矩形围堰的波浪荷载特点进行了研究。吴加云[16]同样基于绕射理论估算了八边形钢围堰的波浪力。陈上有[17]通过势流绕射理论和边界积分方法对大尺度矩形和圆端矩形截面基础进行了研究。遆子龙[18]利用三维绕射理论结合现场实测数据研究了跨海桥梁哑铃形围堰波浪压力的分布特点。叶乔丹[19]通过数值模拟软件,对施加有防撞装置的桥墩在波浪冲击下的工况进行数值分析,发现施加有防撞装置的下部结构所受波浪荷载增大。何海峰[20]基于数值模拟分析,采用Morison方程和绕射理论计算桩基、承台和围堰受到的波浪荷载,分析了群桩基础在波浪荷载的受力性能。

以上研究中均涉及各种桥梁基础波浪力作用,但对于相同迎浪断面下不同形状基础波浪力作用之间的差异性缺乏横向对比。利用数值模拟手段,在相同波浪条件下建立不同形状桥梁基础的数值模型,保证其迎浪方向上波浪断面相同,在此基础上对比其受力特点的差异,并结合结构周围处的三维流场数据对局部流速变化加以分析。

1 数值模型

采用CFD软件Flow3d建立三维数值水槽模型,并设置边界条件以及初始条件等相关设置进行数值模拟计算。在模型验证上使用与YANG等[21]试验研究模型一致,缩尺比为1∶100。验证模型有效性后,为避免缩尺效应的影响,后续不同截面的桥梁基础均采用足尺模型进行相关研究。具体计算工况见表1。

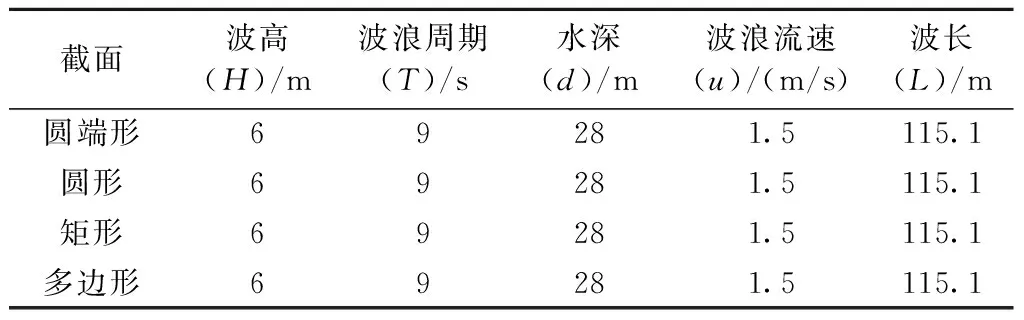
表1 计算工况Tab.1 Working condition for calculation

1.1 控制方程

将流体视为不可压缩流体,同时考虑流体的黏性,以得到波浪与结构物相互作用时,结构物附近的流动状态。因此,在计算区域中,流体的运动控制方程为Navier-Stokes方程。在方程中引入面积参数A和体积参数V表示软件中的FAVOR网格处理方法,得到三维情况下流体运动控制方程,即

(1)

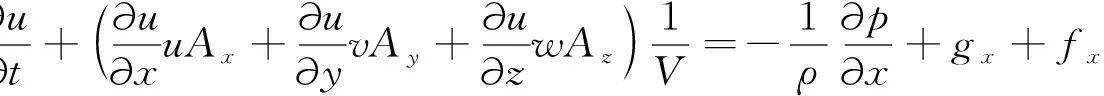
(2)

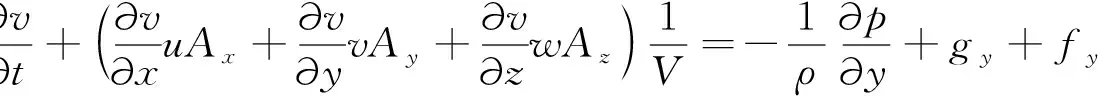
(3)

(4)

式中,Ax,Ay,Az分别为x,y,z方向上的流动面积分数;u,v,w分别为x,y,z方向上的速度分量;gx,gy,gz分别为x,y,z方向上的重力加速度分量;fx,fy,fz分别为流体黏性力引起的x,y,z方向上的加速度分量;V为流体体积分数;ρ为流体密度;p为波压力;t为时间变量。

采用改进后的RNGk-ε模型来实现流体运动控制方程的封闭,如下

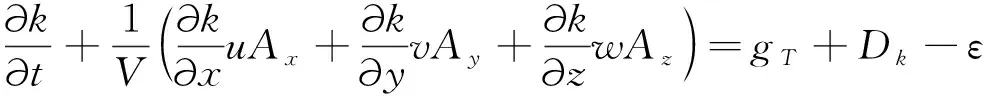
(5)

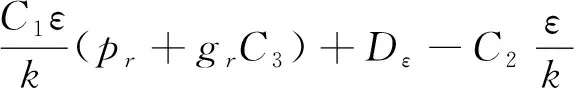
(6)

式中,k为湍流动能;ε为湍流耗散率;pr为平均流动压力;Dk,Dε为扩散系数;C1,C2,C3为常系数,取值为C1=1.44,C2=1.92,C3=0.20。

为追踪自由表面的运动,定义函数φ为一个单元内的流体体积与该单元体体积之比,φ是时间和空间的函数,即φ=φ(x,y,z,t),在三维情况下,可以表示为

(7)

当网格单元为流体内部单元,单元内充满流体,则函数φ=1;当网格单元为流体外部的单元,单元内不含流体,则函数φ=0。

1.2 边界条件

本研究验证采取的三维数值模型如图1所示,其中D为结构物迎浪方向的宽度。在三维数值波浪水槽的6个边界面上进行边界条件的设置。其中入口为造波边界,在网格边界处输入规则波的参数条件,如波高和波周期等。出口为出流边界,在此处设置消波段减弱波浪反射的影响。水槽两侧为对称边界。水槽底部为固壁边界,顶部为压力边界,以保持水槽范围内自由液面的稳定。

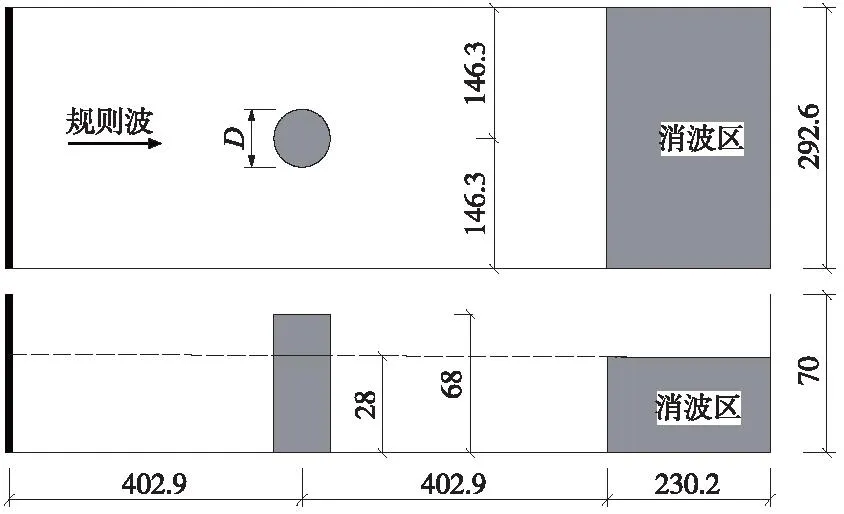
图1 数值模型设置示意(单位:m)Fig.1 Parameters of numerical model( unit: m )

在数值计算中,足尺模型设定通用网格尺寸的大小为,Δx=1.15 m,Δy=2.79 m,Δz=1.1 m。其中加密区域设置在结构物周围,加密区域长度在结构物中心左右1.5倍波长范围内变化,总长度为3倍波长;宽度范围为结构物中心左右1.5倍横桥向投影长度,总宽度为3倍横桥向投影长度;高度以初始水深为起点上下一个波高高度为范围,总高度为2倍波高高度。则加密区域网格尺寸的大小为Δx=0.75 m,Δy=2.09 m,Δz=0.6 m。

不同截面结构要保证截面宽度D和入水深度一致,使得不同结构具有相同的迎浪面积,截面尺寸如图2所示。在后续研究中,采用不同截面结构进行相关研究,其中结构的横桥向投影长度D与波长L比值为0.363,在0.295～0.652之间,且大于0.2;水深d与波长λ比值为0.243,大于0.15,根据《港口与航道水文规范》[6]可认定为大尺度结构。

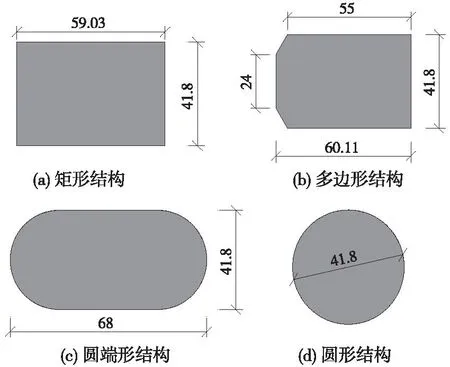
图2 各结构模型尺寸(单位:m)Fig.2 Model size( unit: m )

1.3 模型验证

根据YANG等[15]得出规则波浪对大尺度圆端形结构作用的实验数据,在工况为T=0.9 s、H=0.06 m、d=0.28 m条件下,采用1.2节中描述边界条件,进行数值模型有效性的验证。

图3展示了数值模拟产生的波面曲线与实验测得的波面曲线对比,得出数值结果与试验结果拟合情况良好,波面稳定,证明了数值水槽造波的有效性。

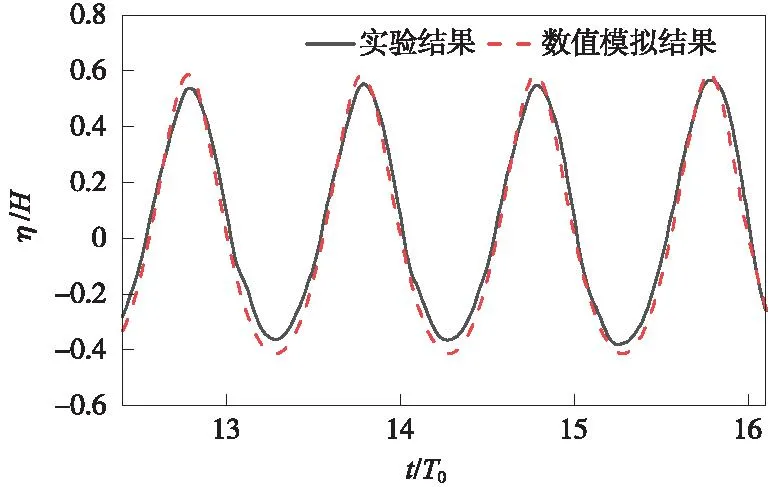
图3 波面结果对比Fig.3 Comparison of calculated and test results of wave surface

图4展示了圆端形结构在波浪入射角θ为45°所受波浪力的数值结果与试验结果对比。根据对比结果,数值模拟得出的波浪力与试验结果存在较小的差异,但相对误差较小且总体变化趋势保持一致。因此,本研究采用的数值计算模型可以较为准确地模拟波浪对桥梁圆端形基础的作用。

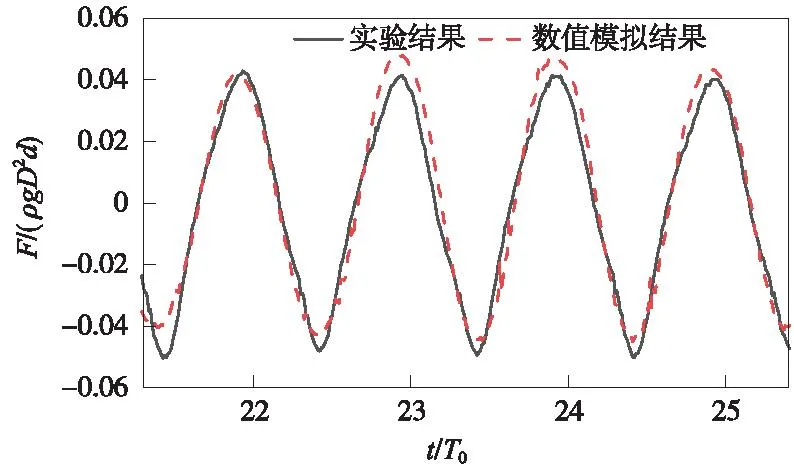
图4 波浪力结果对比Fig.4 Comparison of wave forces

2 计算结果

2.1 受力分析

为对比不同截面桥梁基础结构所受总水平波浪力的差异,对圆端形、矩形、多边形及圆形结构进行研究。在数据采集方面,当规则波浪力达到稳定后,选取连续的5个波浪力峰值及谷值取其平均数作为结构所受最大总水平波浪力,不同截面形式围堰结构的波浪力数据统计如图5所示。

图5 规则波流作用下各结构受力Fig.5 Regular wave induced forces on structures

将不同截面桥梁基础的受力进行比较,由图5可知,圆形结构所受水平波浪力最小,圆端形结构次之,矩形结构所受的水平波浪力最大。其中矩形结构所受的总水平波浪力幅值较圆形结构增大10%左右。圆端形和圆形结构的迎浪面为曲面,能够很大程度上缓解波浪的冲击,而矩形和多边形结构的迎浪面为直面,缓解波浪冲击能力较弱,但多边形存在斜边能够在一定程度上减小波浪冲击力,因此受力要小于矩形。从工程实际的角度看,圆形和圆端形结构在相同迎浪宽度下所受水平波浪力均较小,采取圆弧形的迎浪面能够有效减小波浪荷载。

2.2 流场特性对比研究

为进一步研究不同截面基础受波浪作用时的周围流场及相关水力特性,继续对足尺圆端形、圆形、矩形以及多边形结构进行对比研究。图6为不同截面模型的受力时程对比,选取各个截面基础受力达到稳定的时间段,并分别绘制稳定段波峰和波谷处结构周围流场流速分布,如图7和图8所示。

图6 不同截面形状结构受力时程对比Fig.6 Comparison of time history curves of wave current forces on different section shape structures

图7 稳定段波峰处结构周围流速分布云图Fig.7 Distribution of flow velocity surrounding pile at peak of waves

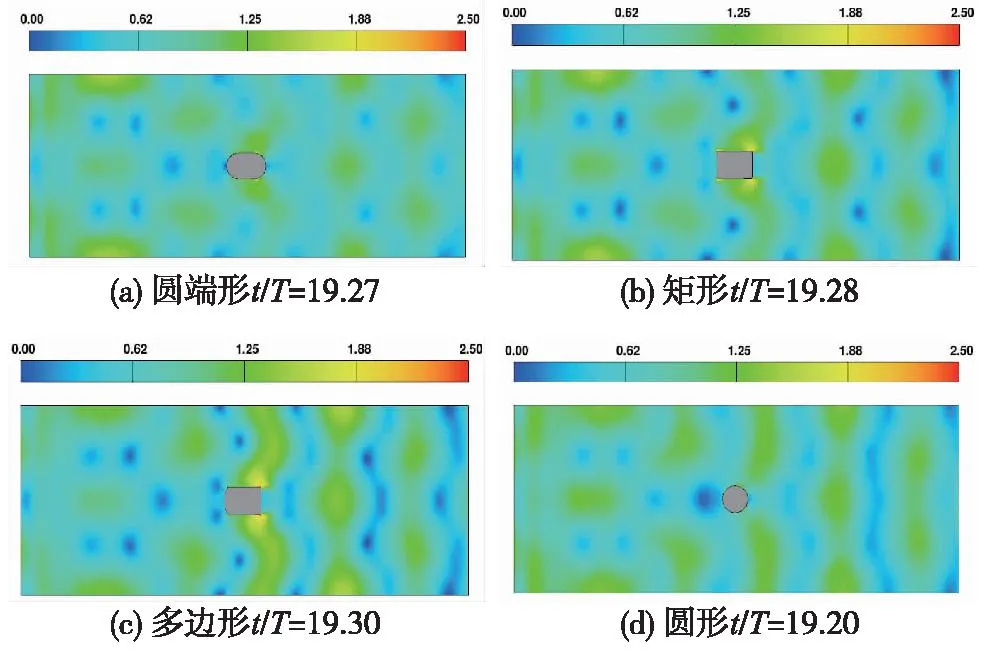
图8 稳定段波谷处结构周围流速分布云图Fig.8 Distribution of flow velocity surrounding pile at trough of waves

根据图6选取稳定时间段的受力峰值与谷值的时间点,在图7和图8中绘制该时间点结构周围流速分布云图。由图7和图8可知,波浪作用于桥梁时,基础结构周围会产生明显的绕流作用,在结构尾部产生漩涡,使得部分位置处的流速明显增大,且出现流速集中现象。这种现象多出现在结构两侧以及转角位置。其中矩形结构流速集中现象最为明显,其在波峰时刻的结构前端两角位置以及波谷时刻的结构后端两角位置均出现了明显的流速集中现象,多边形结构周围也出现了类似情况。圆形结构能够大幅度地削减这一现象,而圆端形结构相较于圆形结构的消减能力弱一些,仅在结构两侧转角位置有较弱的流速集中现象。矩形结构以及多边形结构流速最大处分别集中在结构的棱角处,同时能够清晰地观察到相较于矩形结构,采用多边形并未能够改善流速集中现象,这与多边形结构迎流面尺寸较大有关。该流速分布特性与前文中不同结构的受力特点相对应。

图9和图10展示了结构周围二维速度矢量分布,从而更好地描述结构周围流场特性。通过观察不同截面尺寸结构的流速矢量分布,可以看出,不同结构的流速矢量分布特点基本与流速分布图中对应,在图8中出现流速增大和流速集中的位置均发现有流速矢量在此处汇聚。流速矢量的汇聚主要出现在结构物的两侧以及转角位置。在圆形和圆端形结构周围的流速矢量分布较为均匀。而在矩形和多边形的转角区域可以看出,流速矢量呈现出明显向转角后侧汇聚的趋势,流速矢量在该位置的分布较为集中。

图9 稳定段波峰处结构周围流速矢量分布Fig.9 Velocity vector distribution surrounding pile at peak of waves

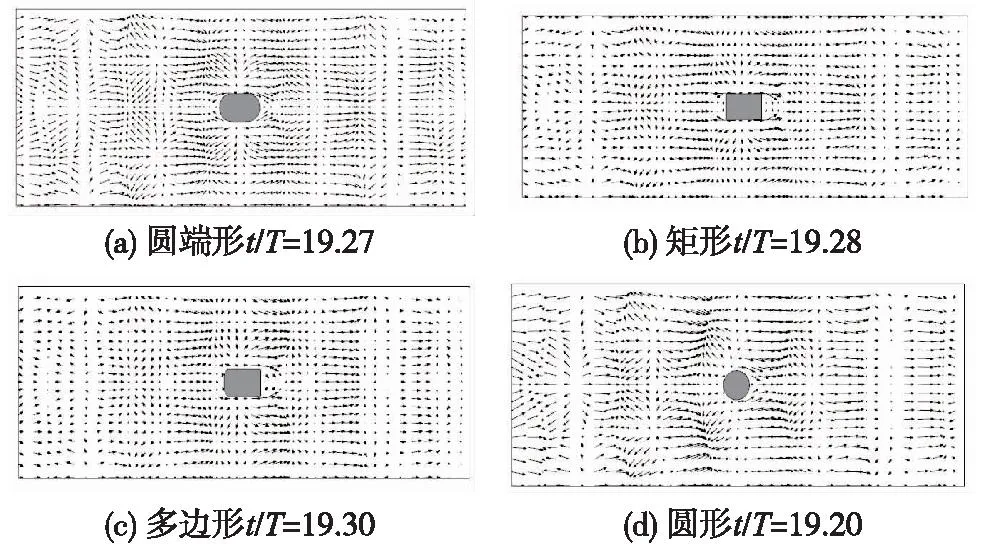
图10 稳定段波谷处结构周围流速矢量分布Fig.10 Velocity vector distribution surrounding pile at trough of waves

2.3 规范计算对比

工程中桥梁大尺度结构波浪力的计算主要参照JTS 145—2015《港口与航道水文规范》,规范中给出了大尺度圆柱的计算公式,并在附录R中给出了方柱波浪力的计算方法。对于其他结构形式的桥梁基础,规范中则按照迎浪面积代换为等效圆柱或方柱进行计算。按照规范计算得到的等效圆柱波浪力为4.08×107N,相较于数值模拟结果大23%～29%,按照等效方柱计算得到的波浪力为3.60×107N,相较于数值模拟结果大10%～13%。由此可见,对于相同迎浪面积下不同形状桥梁基础结构,按照规范进行等效计算得到的波浪力相对较大,而基于此数据进行桥梁结构的工程设计偏保守,但相对地,该计算结果服务于结构设计留有充足的波浪荷载余量,安全性较高。

3 结论

通过对相同迎浪面积下不同截面形式桥梁基础受到的波浪力及结构周围的流场分布进行了相关分析,得出如下结论。

(1)相同迎浪面积下4种不同截面形式的结构所受到水平波浪力中以圆形结构为最小,圆端形结构次之,矩形结构为最大,其总水平波浪力幅值较圆形结构增大10%左右。从工程设计的角度看,较小的波浪荷载和动力响应对于结构是更有益的,采用圆弧形的迎浪面有助于减小结构的波浪荷载。

(2)桥梁基础在波浪的作用下,结构周围会产生明显的绕流作用,使得部分位置处的流速明显增大且发生流速集中现象,在结构两侧以及转角位置尤为明显。矩形结构的这一现象最为突出,多边形结构的情况与之类似,而圆形及圆端形结构的流速集中现象则相对较弱。该流速分布特性与不同基础结构的受力特点相对应。圆弧形的结构设计有利于消减桥梁基础受波浪作用时局部位置处的流速增大和流速集中现象。

(3)基于规范对不同结构形式的桥梁基础进行计算,结果发现,按照规范的等效圆柱方法算得的波浪力比数值模拟结果大23%～29%,按照等效方柱方法计算得到的波浪力比数值模拟结果偏大10%～13%。