高速铁路箱式路基加腋对结构静力特性的影响

刘晶磊，刘佳凡，周玮浩，夏 彬，张业荣，张伯扬，张文祥

(1.河北建筑工程学院,河北张家口 075000; 2.河北省土木工程诊断、改造与抗灾重点实验室,河北张家口 075000;3.河北省寒冷地区交通基础设施工程技术创新中心,河北张家口 075000)

引言

随着我国高速铁路工程的不断发展,高速铁路铺设里程数迅速增长,传统高速铁路路基[1-2]具有平顺性好、连续性好等特点,已被广泛应用。然而,由于传统高速铁路路基难以适应不同地区的差异化地质条件,使得其在建设过程中,整体强度难以达到规定强度指标,且填料耗费多,故急需一种新型路基代替传统路基来满足工程需要。高速铁路箱式路基作为新型路基结构的一种,具有整体性好、强度高、稳定性好、耐久性强、占地面积少等优点,可在恶劣的地质条件下满足高速列车行车要求。祝伟杰[3]总结了箱式路基的结构型式和工程设计,从结构力学角度分析了箱式结构的内力特性与应力传递路径,提出了箱式结构的平面简化受力图。刘平[4]提出一种具有侧向约束的装配箱涵式路基新结构,并对该结构的受力进行了数值模拟分析,指出装配箱涵式路基对沉降控制效果明显,可减少20%～35%的沉降量。肖坦树[5]利用有限元软件ABAQUS建立了3个节点域加腋加固的有限元模型,施加单调荷载和循环荷载,对节点域进行加腋加固,能够有效提高节点域的承载力,减小剪切变形。陈涛[6]通过数值模拟的方式研究了不同节点加腋时的性能变化,指出加腋节点的应力变化与常规节点基本相同,但随着梁腋高度和长度增加,加腋节点的刚度和承载力均有提升。

作为一种新型高速铁路路基结构,箱式路基的受力状态和配筋计算仍处于经验阶段,业内尚无针对该结构的成套计算方法或设计规范。采用控制变量法,针对新型箱式路基结构顶板和竖板连接节点的应力集中现象,研究了三角形腋不同的加腋高度和加腋角度对应力集中部位的应力突变减少值,并找到最优加腋高度区域与加腋角度区域。研究成果可为优化高速铁路路基结构及提升高速铁路路基承载力提供理论依据。

1 箱式路基结构形式

钢筋混凝土箱式路基分别由水平放置在地基上的钢筋混凝土底板;竖直连接在底板上的钢筋混凝土竖板,水平连接在竖板上的钢筋混凝土顶板和竖直固定在底板上的钢筋混凝土短桩组成。钢筋混凝土短桩深入地基土中,用于提升箱式路基的稳定性。顶板和底板均在竖板的外侧延伸预设长度,顶板的延伸长度等于底板的延伸长度。箱式路基结构横截面以及三维效果如图1所示。

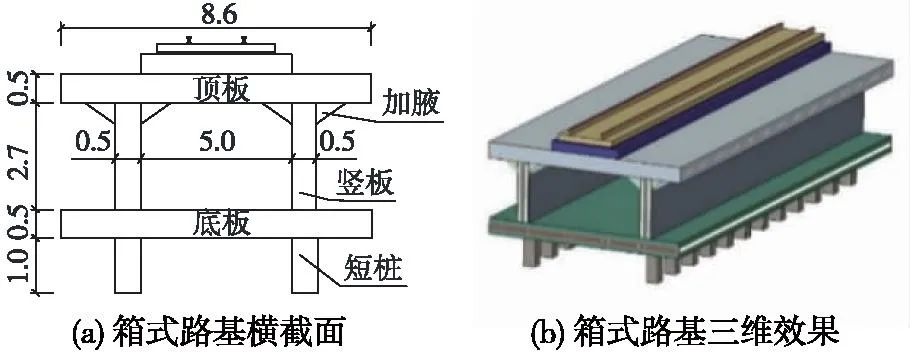
图1 钢筋混凝土箱式路基结构示意(单位:m)Fig.1 Schematic diagram of reinforced concrete box subgrade structure (unit: m)

2 箱式路基模型简化

将箱式路基的计算模型拆分为顶板、竖板、底板和短桩,并根据箱式路基各部件的结构形式和受力情况进行模型简化。

2.1 钢筋混凝土顶板

根据TB10621—2014《高速铁路设计规范》[7]的要求,顶板简化为有两个刚性支座的梁,将顶板的受力部分近似为承受集中荷载,在集中荷载作用下,顶板受力主要以弯矩为主。

2.2 钢筋混凝土竖板

竖板外侧无填土,竖板的受力主要以压应力和弯矩为主,受力方式与简单直线段剪力墙近似[8]。为简化模型,根据简单直线段剪力墙的研究方法对竖板进行研究。

2.3 钢筋混凝土底板

底板的受力主要以弯矩和剪应力为主,为便于研究,将底板视为倒置的连续梁,不考虑底板与地基土之间的相互作用,通过倒梁法[9]对底板进行研究。

2.4 钢筋混凝土短桩

短桩整体都埋置于地基土里,主要的受力为侧阻力和端阻力,为简化模型,采用静压法沉桩[10-12]的方法对短桩进行研究。

3 箱式路基有限元模型建立

3.1 分析模型参数选取

以箱式路基顶板和竖板连接节点为研究对象,H为腋高度;L为腋长度;α为腋角度,所加腋沿线路方向长度为20 m,如图2所示。通过控制变量的方法,先假设最优的腋高度为400 mm,依次增大腋角度,通过分析节点处的应力集中减小值确定最优腋角度区间。之后固定腋角度为60°,依次增大腋高度,通过分析节点处的应力集中减少值确定最优腋高度区间。

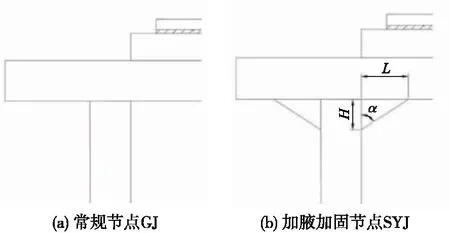
图2 箱式路基节点构造Fig.2 Box subgrade node structure

3.2 模型建立

采用ABAQUS软件进行数值模拟[13-14]。通过细化网格的试验方法划分网格,对加腋部位局部细化,如图3所示。箱式路基各部件之间均通过绑定连接,钢筋均Embedded Region于混凝土部件中。该模型通过在钢轨上间隔5.5 m的距离施加两对大小为85.0 kN静力荷载[15-16]进行加载。箱式路基结构有限元模型的材料属性见表1。

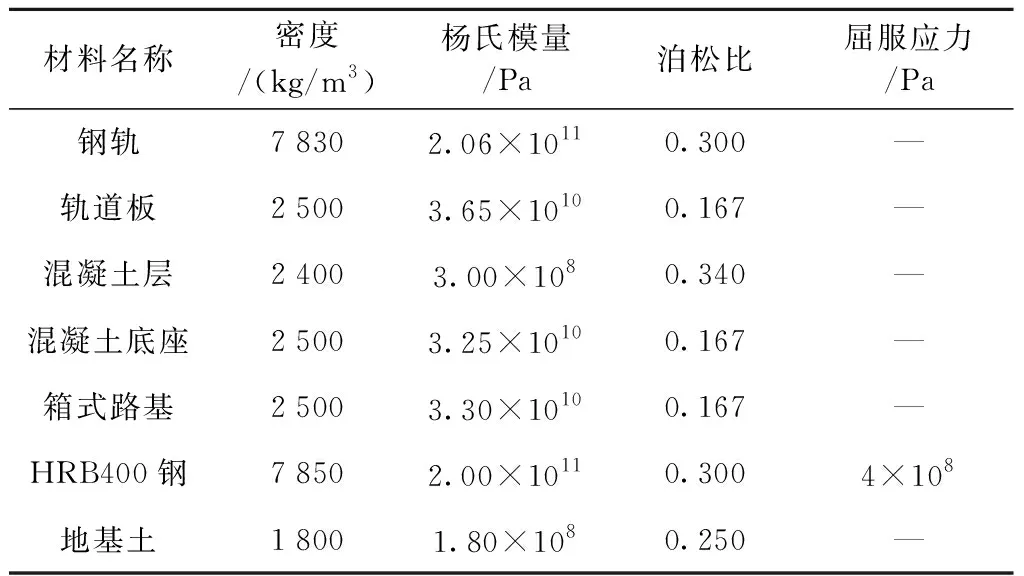
表1 箱式路基结构有限元模型材料属性Tab.1 Material properties of finite element model of box subgrade structure

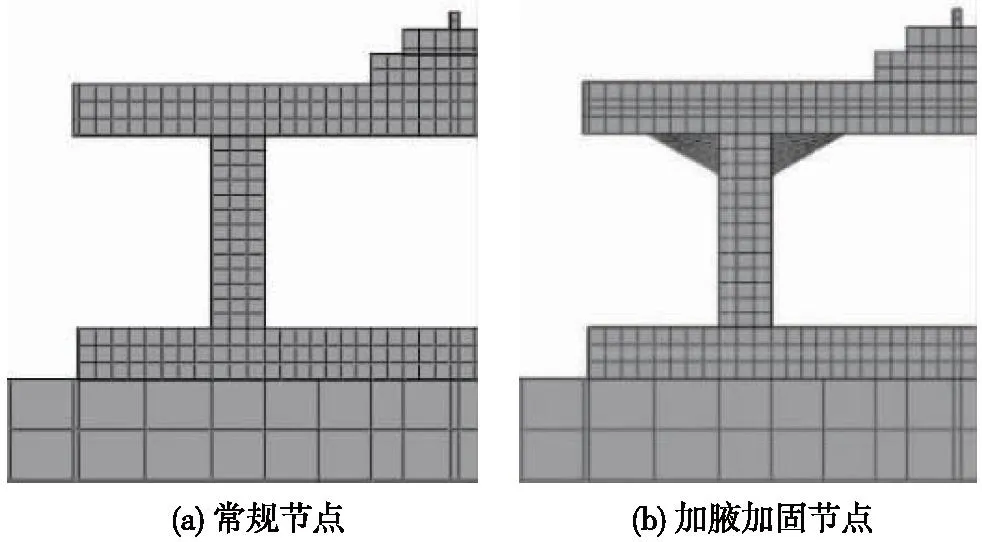
图3 箱式路基加腋节点网格Fig.3 Grid of axillary nodes of box subgrade

4 箱式路基有限元结果分析

通过定义应力突变量降低比Sr值作为应力突变减小效果的评价指标,Sr值为无量纲值,Sr值越小,应力突变减小效果越明显,其表达式如式(1)所示。

Sr=σ1/σ0

(1)

式中,σ1为加腋节点处的应力变化量;σ0为不加腋节点处的应力变化量。

通过控制变量法[17],对上述13个模型进行数值分析[18-19],得到箱式路基未加固节点和加腋加固节点的应力突变值,并对所加不同腋的腋角度和腋高度进行参数化分析[20-21]。

4.1 腋角度对节点影响分析

加腋加固节点的方式比节点处钢筋机械连接的方式在减小应力集中方面效果显著,在工程中备受青睐,不同腋角度对节点处的应力集中又有不同程度的减弱。为研究腋角度变化对节点区域的具体影响,模型先固定腋高度为400 mm,设置腋角度分别为15°,30°,45°,60°,75°。腋角度参数明细如表2所示。

ABAQUS路径创建:选取图1(a)左侧竖板中心线为路径所在直线,起始点为顶板与竖板接触面正上方0.25 m处,结束点为顶板与竖板接触面正下方0.75 m处,路径总长度为1.0 m。

通过有限元软件计算分析,工况GJ节点处应力值较大,应力差值同样较大,工况SJY-4节点处较小的应力值比工况GJ中的多,且应力差值比工况GJ有较大幅度缩小,工况SJY-10节点处较小的应力值比工况SJY-4中的多,且应力差值比工况SJY-4有一定幅度缩小。如图4所示。

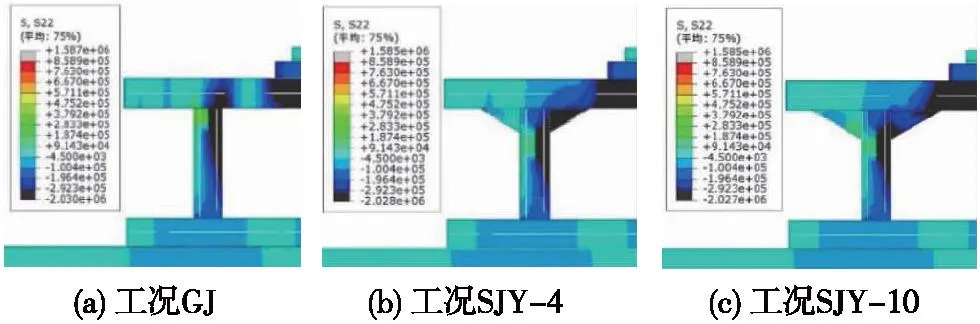
图4 不同工况加腋节点处应力云图(单位:Pa)Fig.4 Stress nephogram at axillary nodes under different working conditions (unit: Pa)

表3给出了当腋长度为400 mm时,不同工况加腋节点处的应力突变量,在此基础上做进一步分析。

表3 不同工况节点应力突变量Tab.3 Sudden change of node stress under different working conditions

未加腋工况与加腋加固工况沿路径方向的应力均增大,两种工况在节点处均产生应力集中,未加腋工况在节点处发生大幅度的应力突变,而加腋加固工况在节点处发生小幅度的应力突变,如图5所示。这说明通过加腋的方式可以有效减小节点处的应力集中现象。

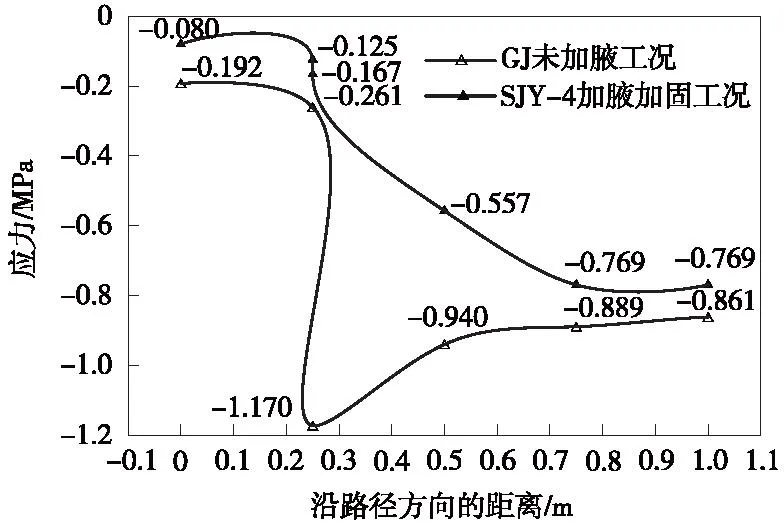
图5 沿路径方向的应力变化Fig.5 Stress variation along the path direction

不同腋角度工况下的Sr值变化如图6所示。由图6可以看出,对节点进行加腋加固后,节点处的应力突变量降低比Sr值均有不同幅度的减小。当加腋角度范围为15°～60°之间时,随着加腋角度增大,Sr值不断减小;当加腋角度范围为60°～75°之间时,随着加腋角度增大,Sr不断增大。在实际工程中,增大腋角度往往带来较大的经济成本,故建议根据工程实际选择适宜的腋角度。

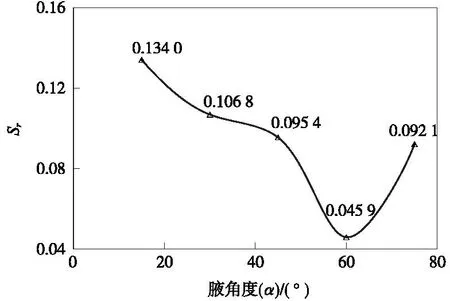
图6 不同腋角度工况的Sr值变化Fig.6 Sr value changes under different axillary angles

综上所述,在考虑经济成本的前提下,当腋高度固定为400 mm时,最优腋角度在SJY-3与SJY-4工况之间取得,即腋角度取值在45°～60°之间时,节点处应力突变量减小值的范围为41.81～86.91 kPa,应力突变量降低比范围为4.59×10-2～9.54×10-2。

4.2 腋高度对节点影响分析

通过上述分析,最优腋角度范围为45°～60°,通过固定腋角度为60°,分析采用不同腋高度对节点处应力突变的影响。设置腋高度分别为100,200,300,400,500,600,700 mm。腋高度参数明细如表4所示。

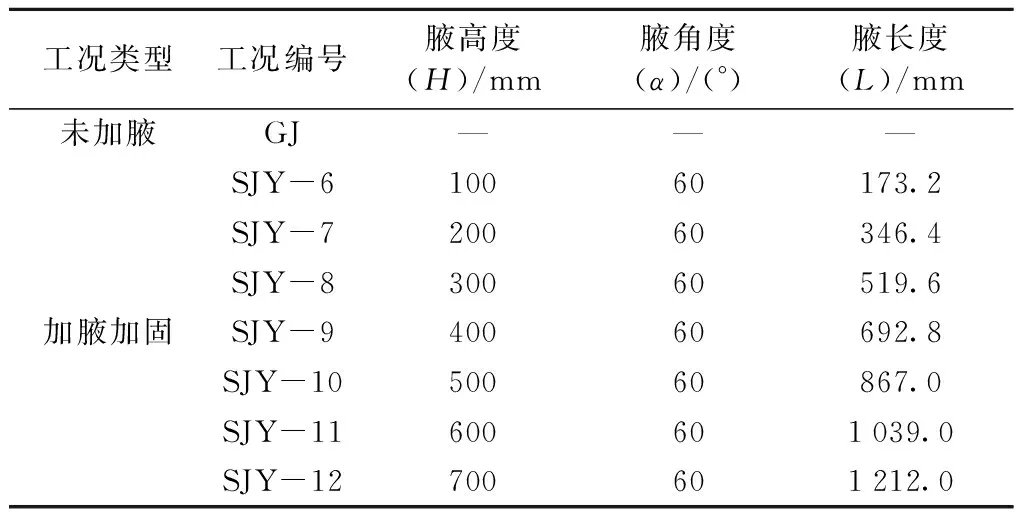
表4 腋高度参数明细Tab.4 Details of axillary height parameters

表5给出了当腋角度为60°时,不同工况的节点应力突变量,在此基础上做进一步分析。

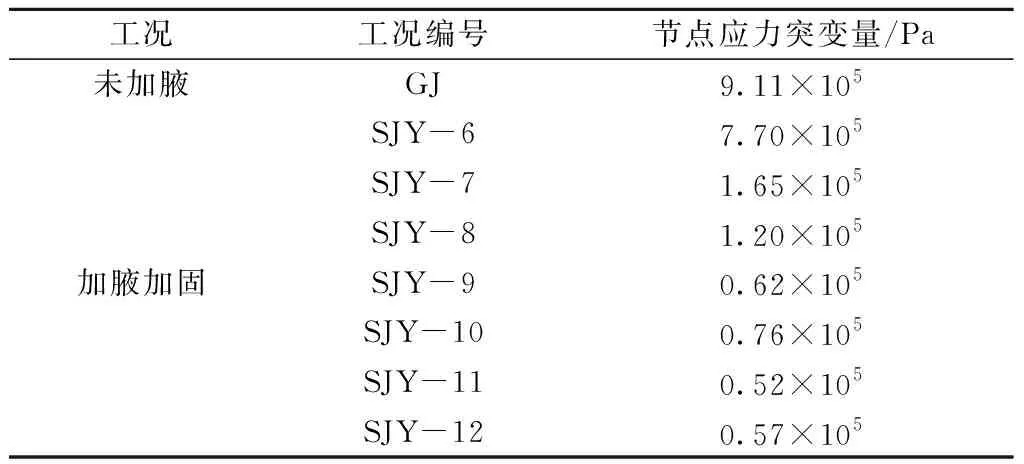
表5 不同工况节点应力突变量Tab.5 Sudden change of node stress under different working conditions

不同腋长度工况下的Sr值变化如图7所示。

图7 不同腋长度工况的Sr值变化Fig.7 Changes of Sr value under different axillary length conditions

由图7可以看出,对节点进行加腋加固后,节点处的应力突变量降低比Sr值均有不同幅度的减小。随着加腋长度增大,Sr值整体上呈减小趋势,当腋长度在100～200 mm时,Sr值下降迅速,当腋长度在200～400 mm时,Sr值下降缓慢。当腋长度为400 mm之后,再增大腋长度,Sr值无明显幅度的减小,即节点处的应力集中减小效果不明显。在实际工程中增大腋长度往往带来比较大的经济成本,故建议根据工程实际选择适宜的腋角度。

4.3 最优加腋工况与其他工况对比分析

通过前文分析,在考虑经济成本的前提下,最优腋角度在45°～60°之间,最优腋长度在300～400 mm之间,取腋角度为60°,腋长度为400 mm作为最优工况加腋。最优工况与其他工况应力突变量如表6所示。

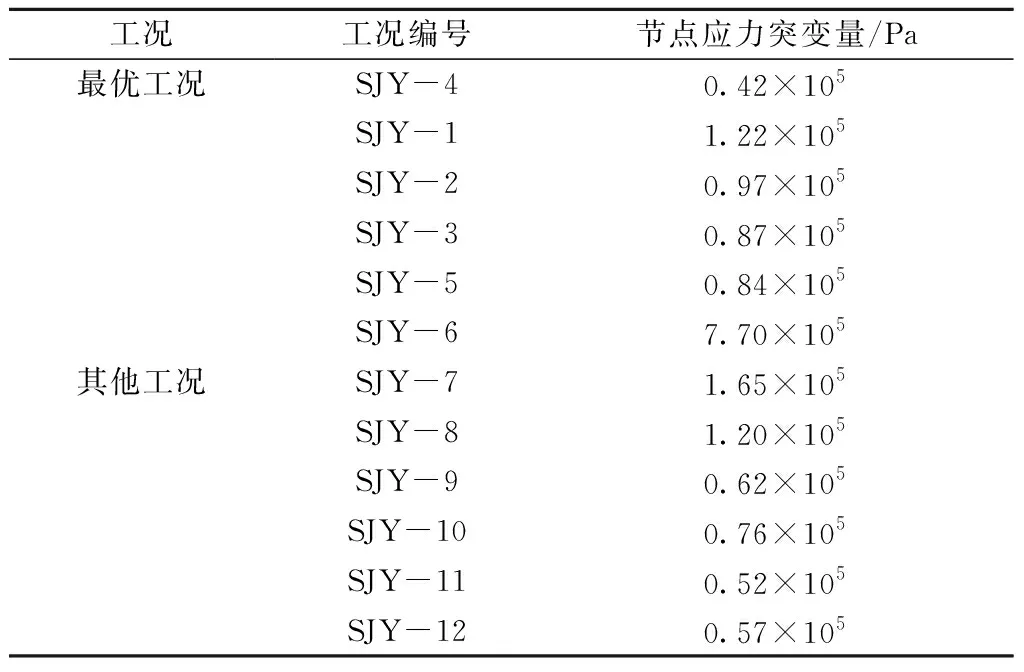
表6 最优加腋工况与其他工况对比Tab.6 Comparison of optimal axillary conditions with other conditions

最优加腋工况与其他工况对比如图8所示。

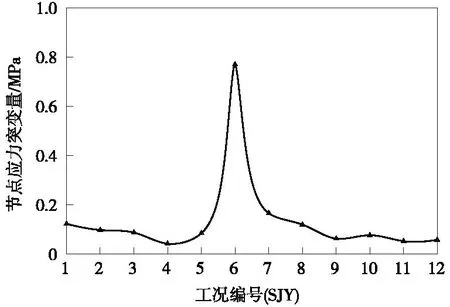
图8 最优加腋工况与其他工况对比Fig.8 Comparison between optimal axillary condition and other conditions

由图8可以看出,在SJY-1工况与SJY-4工况之间,节点处应力突变量呈减小趋势,但减幅较小,在SJY-4工况与SJY-6工况之间,节点处应力突变量呈增大趋势,且增幅较大;在SJY-6工况与SJY-12工况之间,节点处应力突变量整体上呈减小趋势。SJY-4工况相比其他工况具有最小的节点应力突变量,并且和箱式路基竖板高度与厚度、顶板跨度与厚度的变化无关[3]。

5 结论

(1)固定腋高度为400 mm,当腋角度在15°～60°之间时,随着腋角度增大,Sr值不断减小,当腋角度在60°～75°之间时,随着腋角度增大,Sr值不断增大,在考虑经济成本的前提下,最优腋角度在45°～60°之间。在此区间内,节点处应力突变量减小值的范围为41.81～86.91 kPa,应力突变降低比范围为4.59×10-2～9.54×10-2。

(2)腋长度对减小节点处应力集中作用效果显著,随着加腋长度增大,Sr值整体上呈减小趋势,在考虑经济成本的前提下,当腋角度固定为60°时,最优腋长度在300～400 mm之间。在此区间内,节点处应力突变量减小值的范围为62.13～119.33 kPa,应力突变降低比范围为6.82×10-2～1.31×10-1。

(3)箱式路基竖板高度与厚度、顶板跨度与厚度变化时,最优的腋布置形式不会发生变化,结论具有普适性。