生物质循环流化床机组协调系统模型研究

高明明, 刘博通, 张洪福, 王亚柯, 岳光溪

(1． 华北电力大学 新能源电力系统国家重点实验室, 北京 102206;2. 国家能源集团新能源技术研究院有限公司, 北京 102209;3． 华能新能源股份有限公司, 北京 100036; 4． 清华大学 能源与动力工程系, 北京 100084)

在我国现代化发展中,煤炭一直发挥着重要作用,但随着人们物质需求的增长以及煤炭资源的枯竭,煤炭的供需平衡正被打破,价格日益趋高,2021年,我国煤炭需求的缺口约为3亿t标准煤[1],从2019—2021年,动力煤价格增涨近4倍。而新冠疫情、俄乌冲突发生以来,能源进口的风险也不断增大,未来发展新型的可再生能源成为我国安全发展的必经之路。生物质作为唯一一种可再生的化学能源,具有代替传统化石能源的巨大潜力,且在我国产量丰富。由于生物质中的碳是植物生长时从大气中固定下来的,燃烧时又释放出来,因此燃烧后的碳排放近似为零。在我国“双碳战略”大背景下,充分利用生物质资源,推进我国能源结构的转型,有助于我国碳达峰、碳中和目标的早日实现。

近年来,我国生物质发电快速发展,截至2021年年底,我国生物质发电装机累计达到3 798万kW[2],相较于2020年,2021年的生物质发电量同比增长23.6%,且连续3年保持10%以上速度增长,根据2016年印发的《能源生产和消费革命战略(2016—2030)》:到2030年,我国非化石能源发电量力争占到全部发电量的50%[3]。因此,预计在未来较长时间内,我国生物质发电量还会继续保持较快的增长速度。

生物质循环流化床(CFB)锅炉因其对燃料具有良好的适应性,在我国生物质发电领域应用广泛。和燃煤CFB锅炉不同,生物质燃料的水分、灰分和挥发分含量较大[4],热值较低,生物质CFB锅炉内燃烧较不稳定;生物质含硫量较低,锅炉内投入的碳酸钙较少,因此循环物料较少,炉内流化的稳定性较差[5];此外,不同时刻入炉的生物质燃料种类和成分差别较大,热值波动较大,这些都给生物质CFB机组的控制带来了较大影响。因此,建立生物质CFB机组模型,使锅炉能更好地适应燃料的变化,对生物质CFB机组的稳定运行,提升燃烧的安全性与经济性具有重要意义。

此前关于负荷的研究,主要集中在燃煤锅炉,建模方法主要分为机理建模和数据建模:前者可以通过对锅炉内的区域分区建模,针对不同的区域采用不同的传热参数和模型进行锅炉吸热量的计算[6],也可以基于机理分析,通过质量守恒和能量守恒,将锅炉内的燃烧通过燃烧速率平均值来计算[7];后者则采用深度学习、机器学习、回归模型等方法建模[8],且模型精度较高,但在负荷段较低时,当运行特性发生改变,建模精度易出现下降。

笔者从机理出发,深入研究了生物质CFB机组锅炉侧、汽水侧和汽轮机侧的动态过程。分析了锅炉内化学燃烧反应过程,对炉膛发热量进行了计算,对汽水侧的动态过程进行了适当简化,建立了汽水侧集总参数模型。结合汽轮机动态特性,建立了生物质CFB机组负荷控制系统模型,并利用电厂实际运行数据,通过稳态工况推导、遗传算法,实现了对模型参数的辨识和部分未知函数关系的确定。最后通过模型泛化验证,验证了模型的准确性,并在Simulink仿真平台进行阶跃试验,对模型的仿真结果作进一步的分析。

1 生物质循环流化床锅炉介绍

1.1 模型结构

以某30 MW生物质CFB机组为研究对象,整体的发电过程如图1所示。锅炉为山西太原锅炉厂生产的TG-130/13.7-S1型超低排放循环流化床汽包锅炉,配有4台辊式给料机,冷渣器冷渣,额定负荷下螺旋给料机的给料量为50 t/h,无外置床,锅炉内布置有屏式受热面。锅炉尾部烟道采用单烟道,单次再热,过热器配置三级喷水减温装置。正常工况下,蒸汽额定蒸发量为130 t/h,负荷为30 MW,主蒸汽质量流量为98.3 t/h,主蒸汽压力为13.7 MPa,过热蒸汽、再热蒸汽的出口温度均为540 ℃。

图1 生物质CFB机组示意图

1.2 生物质CFB锅炉内燃烧蓄能过程

生物质燃料碳含量较少,挥发分含量较高。根据文献[9],生物质挥发分的平均质量分数为75%,固定碳质量分数在15%左右,因此生物质CFB锅炉内的固体燃料存量较少,蓄能较小,在给料量波动时,锅炉内的温度波动较大。同时,不同燃料挥发分的裂解机理复杂且产物不同,热解产物的产量会随温度和压力变化而变化,因此,不同时刻生物质燃料的热值较不稳定,炉膛发热量波动较大,床温波动较大。

生物质燃料进入炉内后会率先吸热脱出水分,水分越大,水汽带走的热量越多,锅炉内温度越低;水分脱出后,挥发分热解脱出,低于500 ℃时,热解产物主要是焦油、CO、H2和CmHn,在500～800 ℃,焦油会进一步转化成CO、H2、CH4和C2H4等气相产物[10]。生物质燃料热解过程如图2所示。

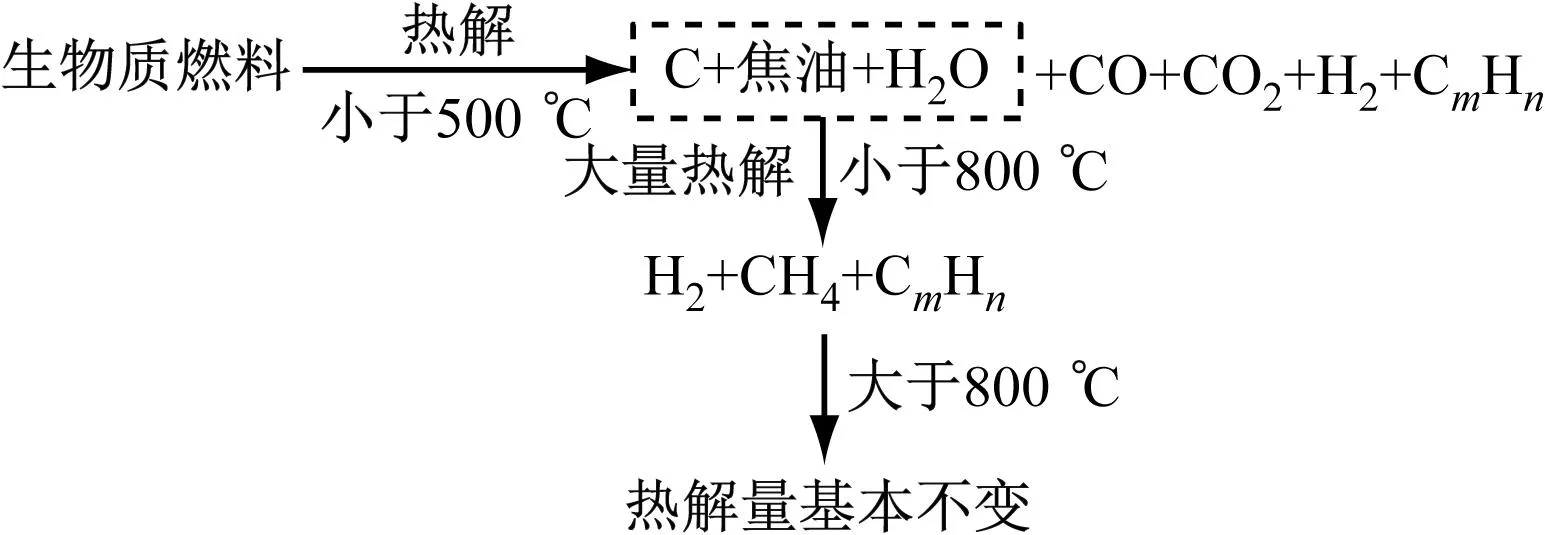
图2 生物质燃料热解过程

在以往的研究中,考虑到生物质CFB机组负荷变化较小,锅炉内稳态温度一般在780～850 ℃,热量较高,挥发分能在0.45～0.55 s内完成热解析出[11],因此忽略挥发分的析出过程,且认为挥发分析出后能在极短的时间内燃烧耗尽,但在动态过程中,给料量剧烈变化,炉内氧量、温度变化较大,挥发分燃烧速率变化较大,若按瞬时完全燃烧计算,易产生较大误差。

挥发分热解析出后会在燃料表面快速燃烧。随着温度的上升,燃料中的碳达到着火温度,但挥发分的燃烧阻碍了氧气向内部的扩散[12],因此碳与氧气接触困难,燃烧较滞后。当挥发分的热解析出速率小于氧的扩散速率时,碳将与挥发分同时燃烧。在研究中一般将该过程简化,认为挥发分率先燃烧,然后是碳开始燃烧[13]。

和燃煤CFB锅炉一样,生物质中的碳颗粒燃烧后并不能迅速燃烧耗尽,从开始燃烧到破碎再到完全燃烧中间要经历较长时间,因此,生物质CFB锅炉内也存有一定量未燃尽的碳,这些碳是锅炉内碳发热量的主要来源,给料中碳的发热量只占当前锅炉内碳发热量的极少部分。锅炉内的发热量可以认为是碳和挥发分燃烧放热之和[14]。

2 模型建立

2.1 挥发分燃烧放热模型

挥发分热解产生的可燃物气体种类繁多,成分主要包括CO、H2和碳氢化合物。由于挥发分热解的机理复杂,要准确计算这些成分的产量较为困难,因此,本文模型中对挥发分的计算进行简化,认为挥发分的碳氢化合物全部转化为CO、H2和CH4,产物产量按照固定的质量分数来计算。根据文献[15],锅炉内CO、H2和CH4的整体燃烧速率可写为

(1)

(2)

(3)

式中:RCO、RH2、RCH4分别为挥发分CO、H2、CH4的燃烧速率,kg/s;kCO、kH2、kCH4分别为挥发分CO、H2、CH4的反应动力常数;cCO、cO2、cH2O、cH2、cCH4分别为各气体组分CO、O2、H2O、H2、CH4的物质的量浓度,kmol/m3

考虑到燃料在进入锅炉前会进行脱水处理,因此本文假设锅炉内的水分浓度波动较小,计算时将水分浓度当作定值来计算。

反应动力常数与温度有关,故各组分的反应动力常数分别写为

(4)

(5)

(6)

式中:T为床温,K;k1、k2、k3分别为CO、H2、CH4的反应动力系数。

进入锅炉内的挥发分一部分经燃烧消耗掉,一部分被烟气带出。基于质量守恒,挥发分各组分的物质的量浓度可以写为

(7)

(8)

(9)

式中:kq-CO、kq-H2、kq-CH4分别为CO、H2、CH4的质量分数系数,和各组分在燃料中的质量分数有关;F(t)为某一时刻进入炉膛的燃料量,kg/s;kb-CO、kb-H2、kb-CH4分别为挥发分CO、H2、CH4的燃烧消耗系数;kf-CO、kf-H2、kf-CH4分别为烟气带走的挥发分CO、H2、CH4的比率系数;Air为总风量,m3/s;t为时间,s。

挥发分在某一时刻的燃烧放热量Q2为

Q2=RCOHCO+RH2HH2+RCH4HCH4

(10)

式中:HCO、HH2、HCH4分别为挥发分CO、H2、CH4的热值,分别取为10.08 MJ/kg、124.24 MJ/kg、50.02 MJ/kg。

2.2 碳燃烧放热模型

根据前文的分析,生物质CFB锅炉内存有未燃尽的碳,这些碳称为即燃碳[16]。根据质量守恒,锅炉内即燃碳量为

(11)

式中:B(t)为锅炉内的即燃碳量,kg;ηB为生物质燃料收到基碳的质量分数,%;Rc为即燃碳的燃烧速率,kg/s;D(t)为排渣中的碳含量,kg/s。

考虑到生物质燃烧后残渣剩余量较少[17],故简化模型,将式(11)写为

(12)

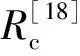
(13)

式中:Nc为锅炉内的碳颗粒个数;Mc为碳的摩尔质量,kg/kmol;dc为碳颗粒的平均直径,m;kc为碳颗粒的燃烧速率常数;ρc为碳颗粒的密度,kg/m3。

碳颗粒的燃烧速率常数kc与燃烧反应速率和氧扩散速率有关。由于氧扩散速率计算复杂,因此本文简化模型,重点考虑温度对碳颗粒的燃烧速率常数的影响,因此,碳颗粒的燃烧速率常数kc参照燃煤CFB锅炉碳的燃烧速率常数[19]写为

kc=0.513Texp(-9 160/T)

(14)

吹入锅炉内的氧气,一部分被燃料燃烧消耗,一部分被风吹出炉膛,故氧浓度的计算用式(15)[20]表示:

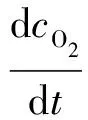
(15)

式中:V为炉膛容积,m3;kq为摩尔换算系数,kmol/m3;kf为与烟气流量有关的比率系数。

某一时刻即燃碳的放热量为

QB=RcHc

(16)

式中:QB为某一时刻锅炉内即燃碳燃烧放出的热量MJ/s;Hc为碳的热值,MJ/kg。

生物质电厂的燃料来源复杂,为减小燃料的成分含量变化和给料量数据与实际的偏差对计算的影响,笔者引入给水流量与给料指令的比值对燃料中碳的质量分数进行矫正,矫正的计算式[21-22]写为

(17)

2.3 传热计算模型

根据能量平衡,锅炉内的发热量一部分被烟气和工质带走,一部分被排渣带走,剩下的以床温的形式存储在床料中,将被烟气和排渣带走的能量视为热量损失,则能量平衡方程可以写为

(18)

式中:cs为床料的比热容,MJ/(kg·K);ms为锅炉内的床料质量,kg;η为锅炉热效率;Qt为某一时刻水冷壁的吸热量,MJ/s;Q2为某一时刻锅炉内挥发分的燃烧发热量,MJ/s。

用主蒸汽温度代表金属壁和工质的集总参数,水冷壁的吸热量Qt可以表示为

(19)

式中:k4为平均传热系数;Tst为主蒸汽温度,K;n为模型系数。

2.4 汽水侧计算模型

汽水侧的蓄能主要存储在汽包中,汽包的蓄能能力用锅炉的蓄热系数表示。汽包压力对锅炉的发热量反应灵敏,因此选用汽包压力作为集总参数来反映工质的能量变化。汽水流程结构如图3所示。图中:hfw为给水焓,kJ/kg;qm,sw为减温水质量流量,kg/s;hsw为减温水焓,kJ/kg;qm,st为主蒸汽质量流量,kg/s;hst为主蒸汽焓,kJ/kg;qm,s为喷水减温前过热蒸汽质量流量,kg/s;hs为喷水减温前过热蒸汽的焓,kJ/kg;pm为汽包压力,MPa。

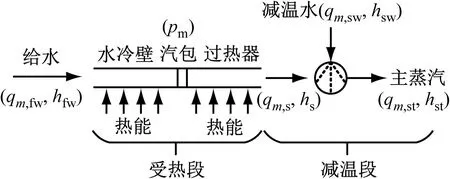
图3 汽水流程图

根据图3,输入的热量来自锅炉发热量、给水的能量和减温水的能量,输出的能量为进入汽轮机做功的能量。基于能量守恒,得到汽水侧的能量平衡方程为

(20)

式中:Cb为锅炉的蓄热系数,MJ/MPa;Qin为某一时刻锅炉的吸热量,kJ/s。

锅炉的吸热量Qin可以写为水冷壁吸热量的线性函数:

Qin=kinQt

(21)

式中:kin为锅炉总的吸热量增益。

过热器中的压降通常写为压力的函数,但在负荷较低时,其压降更适合写为负荷的函数[23],故采用式(22)的函数关系来表示压降:

pm-pst=g(Ne)

(22)

式中:pst为主蒸汽压力,MPa;Ne为机组负荷,MW。

2.5 汽机侧计算模型

主蒸汽流量可以通过与汽轮机阀门开度、主蒸汽压力和主蒸汽密度之间的函数关系计算,主蒸汽密度又可以写为主蒸汽压力、主蒸汽焓值的函数,故:

(23)

式中:ut为汽轮机阀门开度,%;ρst为主蒸汽密度,kg/m3;λ、α为模型参数。

主蒸汽进入汽轮机中做功,其能量的释放具有一定的惯性,因此,机组负荷和主蒸汽压力、汽轮机阀门开度之间的关系可以用一阶惯性环节来表示:

(24)

式中:Cn为汽轮机动态时间,s;kn为汽轮机阀门开度增益。

3 模型参数辨识

模型中需要辨识的参数有:Cb、kin、Cn、kn、kB,以及模型中的函数关系式Qt、g(Ne)、qm,st。

3.1 静态参数识别

为识别模型的静态参数,表1给出了机组在30 MW稳态时各个参数的运行数据。

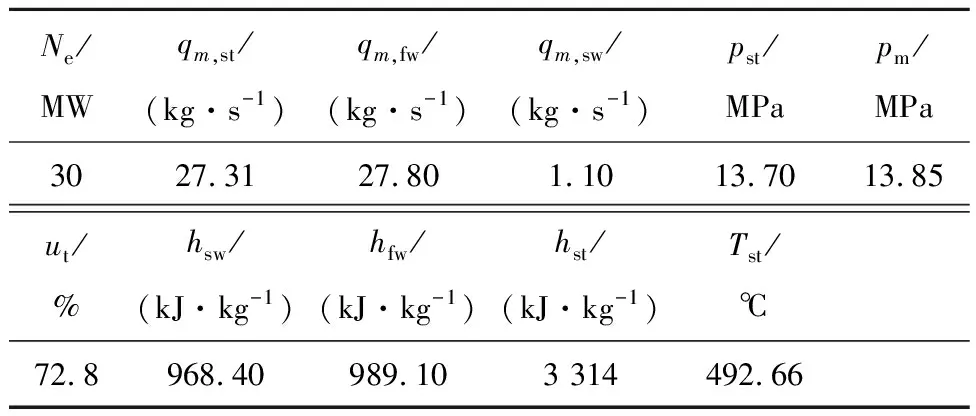
表1 稳态运行时的参数值

基于建立的模型,可以得到稳态下的静态方程:

(25)

(26)

式中:带*的是变量在稳态时的数值。

代入各物理参数稳态时的数据,可以得到锅炉总的吸热量增益kin和汽轮机阀门开度增益kn。在运行数据和回归分析的基础上,可以识别得到Qt、g(Ne)、qm,st函数,上述参数和函数的识别结果分别为

kin=1 770

kn=3.007 5

3.2 动态参数识别

将负荷在动态过程变化的历史数据代入辨识得到的静态参数,采用遗传算法闭环辨识动态模型参数,目标函数J(x)为

(27)

式中:Δpst为计算主蒸汽压力与实际主蒸汽压力之差,MPa;ΔNe为计算负荷与实际负荷之差,MPa;N为动态变化过程中的数据采集量。

遗传算法参数动态辨识的结果为Cb=4 000 MJ/MPa,Cn=60 s。

通过仿真实践,得到式(17)的表达式,煤质校正后的曲线如图4所示,校正后碳的质量分数会在设计值的上下浮动。

(28)

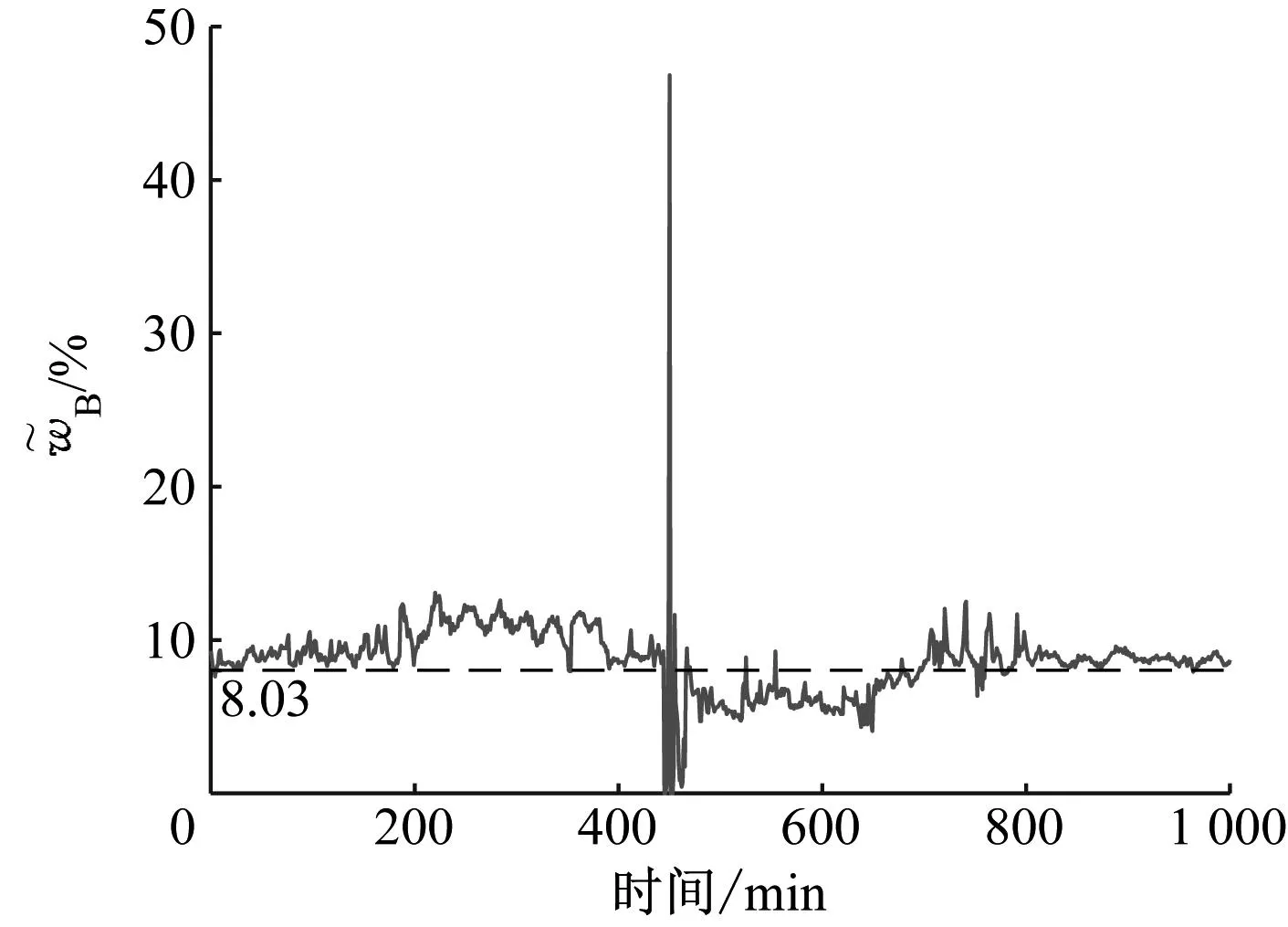
图4 矫正后碳的质量分数

3.3 辨识结果验证

将上述参数代入模型中,燃料中碳的质量分数参照电厂锅炉的设计燃料碳含量,由于挥发分各组分的热解析出量实际值确定较为困难且不同时刻产量也不同,因此挥发分各组分的质量分数通过仿真实践确定,采取仿真时间段内折中的最佳值作为挥发分各组分的质量分数,燃料各成分的含量参照表2。现场采集的数据时间间隔为1 min。模型输出与实际值的对比如图5所示。

表2 生物质燃料参数

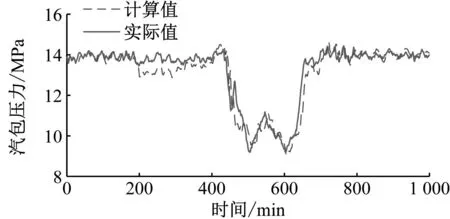
(a) 汽包压力

由模型计算得到的pm、pst、qm,st和Ne相对误差最大值和平均值如表3所示。根据计算结果,汽包压力、主蒸汽压力的平均相对误差均小于3%,主蒸汽质量流量和负荷的平均相对误差均小于4%,模型输出的相对误差平均值在可接受范围内,且模型计算值与实际值的变化趋势一致,可认为模型参数辨识结果较为理想。

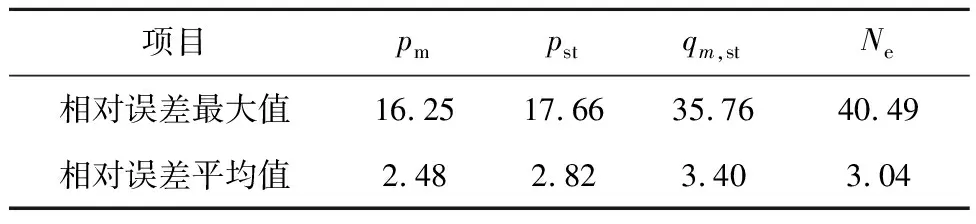
表3 模型输出误差

从图5可知,汽包压力的变化速度较负荷的变化速度慢,汽包的蓄能能力较强。在第200 min附近,主蒸汽压力的计算值下降幅度较大,而实际主蒸汽压力变化不大。分析其原因,锅炉内发热量下降时,汽水侧的部分饱和水和饱和蒸汽能够迅速进入汽轮机做功使压力损失减小,从而缓解了实际主蒸汽压力的波动,而计算中未考虑汽包的蓄能作用,因此计算值相对于实际值波动较大。

4 模型验证

4.1 模型泛化验证

选取一段负荷波动较大的数据进行验证,该时间段内,负荷的最大波动为12 MW,模型结果的对比如图6所示。由图6可知,模型计算值与实际值较吻合,证明模型具有一定的扩展性。其中,主蒸汽压力的最大相对误差为7.90%,平均相对误差为1.69%,负荷的最大相对误差为8.13%,平均相对误差为1.90%,误差大小在可接受范围内,能满足一般控制器的设计要求。

(a) 主蒸汽压力

4.2 模型阶跃试验

为进一步验证模型的动态结果,在额定工况下对模型的输入(给料量、总风量、汽轮机阀门开度)加入5%的阶跃扰动,分别得到机组主要参数(主蒸汽压力、主蒸汽流量、负荷)的响应结果,如图7～图9所示。由图7可知,给料量阶跃上升5%,锅炉内挥发分、即燃碳量上升,放热增大,蒸汽蒸发量增大,因此主蒸汽压力、主蒸汽质量流量、负荷也增大,而随着床温、锅炉吸热量上升并达到平衡,负荷又趋于稳定,进入稳定状态。

图7 模型给料量阶跃响应

由图8可知,当风量阶跃上升5%时,锅炉内的燃烧速率上升,锅炉内蓄能快速释放,主蒸汽压力、负荷上升,但由于给料不变,锅炉内的燃料存量下降,其放热量会在达到峰值后下降并重新达到平衡,主蒸汽压力和负荷也随之下降最后达到稳态值。

图8 模型总风量阶跃响应

由图9可知,汽轮机阀门开度阶跃上升5%时,主蒸汽质量流量迅速上升,主蒸汽压力下降,负荷快速增大,但由于燃料侧发热量不变,主蒸汽压力的减小与汽轮机阀门开度的增大会重新达到平衡,主蒸汽流量和负荷上升到一定值后又回到稳态值。

图9 模型汽轮机阀门开度阶跃响应

同时,从模型的阶跃响应看到,30 MW生物质CFB机组的响应时间较大型燃煤CFB机组的响应时间短。锅炉侧输入的阶跃响应惯性时间较大,从给料量和风量出现5%波动到机组参数达到稳定中间要经历数十分钟,因此实际中需要加入前馈控制,控制参数才能更快地趋于稳定。

5 结论

(1) 建立了30 MW生物质CFB机组协调系统模型,该模型能反映生物质CFB机组变量之间的关系,且模型相对简单,具有一定的适用性。

(2) 模型的辨识结果显示:模型的输出与实际变化趋势一致,汽包压力、主蒸汽压力的平均相对误差均小于3%,负荷、主蒸汽质量流量的平均相对误差均小于4%。泛化验证结果显示,负荷、主蒸汽压力平均相对误差均小于2%。对模型的阶跃试验表明:模型的动态响应符合实际运行经验,证明了模型的有效性,为生物质CFB机组仿真分析、控制器设计和优化提供了理论基础。