运用克拉珀龙方程解决理想气体状态转换和变质量问题

胡东明

(湖北省武汉市新洲区第一中学)

推论1由,得质量,根据质量守恒定律,一定质量的理想气体(状态为p1、V1、T1)分离为两部分气体(状态分别为p2、V2、T2和p3、V3、T3),有,反之亦然.这就是理想气体分态方程.

推论2根据推论1,质量,即对同种理想气体(摩尔质量M相同),质量m与成正比.

推论3由,得密度,即对同种理想气体,密度ρ与压强p成正比,与热力温度T成反比.

下面举例说明如何应用这三个推论解决理想气体状态转换和变质量问题.

1 气体状态的转换问题

例1一热气球(连同吊篮)充气前的总质量m＝180kg,充气后球内空气的体积为V＝600m3.热气球外冷空气的温度为T0＝280K,密度为ρ0＝1.2kg·m－3.已知该气球内、外的气压始终都为p0＝1.0×105Pa,重力加速度大小g取10m·s－2.

(1)热气球刚开始缓慢升空时,气球内热空气的质量;

(2)热气球刚开始缓慢升空时,气球内热空气的温度.

(1)设刚开始升空时,气球内空气的质量为m1,由受力平衡得m1g＋mg＝ρ0gV,解得m1＝540kg.

(2)解法1刚开始升空时,气球内空气的体积为V,设温度为T1,等压转换到温度为T0时空气体积为V2,由盖—吕萨克定律得.转换后的空气与气球外冷空气的压强和温度都相同,则密度相同,空气质量m1＝ρ0V2,解得T1＝373.3K.

解法2由于气球内、外的气压始终都为p0,设开始升空时气球内空气温度为T1,密度为由,得.取热气球外质量为m0的冷空气,设体积为V0,同样密度为,由,得,有ρ0T0＝ρ1T1,解得T1＝373.3K.

解法1采用气体状态转换法,将升空时空气的温度和压强转换到与已知密度的空气的温度和压强相同的状态,根据推论3,空气的密度就相同;解法2直接运用推论3,即“同种理想气体在压强相同的情况下,密度ρ与温度T成反比”.

例2(2023年全国甲卷)一高压舱内气体的压强为1.2个大气压,温度为17℃,密度为1.46kg·m－3.

(1)升高气体温度并释放出舱内部分气体以保持压强不变,求气体温度升至27 ℃时舱内气体的密度;

(2)保持温度27 ℃不变,再释放出舱内部分气体使舱内压强降至1.0个大气压,求舱内气体的密度.

(1)以升高温度后舱内剩余气体为研究对象,设气体质量为m,体积为V1,温度为T1＝(273＋27)K＝300K,密度为,等压转换到原温度为T2＝(273＋17)K＝290K,体积为V2,由盖—吕萨克定律有,得,又因为转换后气体的密度为,解得ρ1＝1.41kg·m－3.

(2)以降压后舱内气体为研究对象,设气体质量为m0,压强为p0,体积为V1,密度为.等温转换到原压强1.2p0,体积为V3,由玻意耳定律有p0V1＝1.2p0V3,得V1＝1.2V3,又因为转换后气体的密度为,解得ρ0＝1.18kg·m－3.

第(1)问气体压强不变,也可以根据推论3,气体密度与温度成反比,有ρ1T1＝ρ2T2,得;同样的,第(2)问气体温度不变,气体密度与压强成正比,有,得

例3一热气球体积为V,内部充有温度为Ta的热空气,气球外冷空气的温度为Tb.已知空气在1个大气压、温度为T0时的密度为ρ0,该气球内、外的气压始终都为1个大气压,重力加速度大小为g.

(1)求该热气球所受浮力的大小;

(2)求该热气球内空气所受的重力;

(3)设充气前热气球的质量为m0,求充气后它还能托起的最大质量.

方法1气体状态转换法

(1)设1 个大气压下、温度为Tb、体积为V的空气质量为m.将这些气体转换为1个大气压、温度为T0的空气,设其体积为V0.

(2)设热气球内的空气质量为m1,将气球内热空气转换为1个大气压、温度为T0的空气,转换后的空气体积为V2.

(3)设该气球还能托起的最大质量为m2,由力的平衡条件得F＝G＋m0g＋m2g,解得

方法2探寻气体密度法

(1)设1个大气压下质量为m的空气在温度T0时的体积为V0,密度为

温度为Tb时的体积为Vb,密度为

由盖—吕萨克定律可得

联立式①②③解得

气球所受的浮力为

联立式④⑤解得

(2)气球内热空气所受的重力

由式④知

联立式⑦⑧解得

(3)设该气球还能托起的最大质量为m2,由力的平衡条件可知

联立式⑥⑨○10可得

方法1第(1)问将排开气体的压强和温度转换到与已知气体的压强和温度相同,根据推论3,其密度就相同.同样的,第(2)问热气球内气体的压强和温度转换到与已知气体的压强和温度相同,运用推论3求解.方法2是直接探寻气体密度,是高考答案给出的解法,式②是一种函数式的写法,认为气体在压强不变的情况下,密度是温度的函数,即,这就是推论3的思想,式④表明一定质量的理想气体在压强相同情况下,密度与温度成反比,这就是推论3.

2 变质量问题

类型1 充气问题

例4如图1所示为喷洒农药用的某种喷雾器.其药液桶的总容积为15L,装入药液后,封闭在药液上方有1atm、2L的空气,忽略打气和喷药过程气体温度的变化.

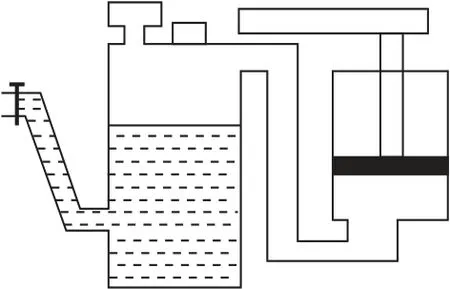
图1

(1)若要使气体压强增大到2.5atm,喷雾器内充气后空气的质量与充气前空气质量之比是多少?

(2)如果压强达到2.5atm 时停止打气,并开始向外喷药,那么当喷雾器不能再向外喷药时,桶内剩下的药液还有多少升? 喷药后喷雾器内剩余空气的质量与充气前空气质量之比是多少?

(1)将2.5atm、2L 空气等温转换到1atm下,由玻意耳定律有p1V1＝p0V2,解得V2＝5L.喷雾器内充气后空气的质量与充气前空气质量之比为.

由于向外喷药过程中,喷雾器内空气的质量没有变化,所以喷药后喷雾器内剩余空气的质量与充气前空气质量之比仍然为.

本题第(1)问将喷雾器内充气后空气的压强和温度转换到与充气前空气的压强和温度相同,其密度就相同,运用推论3求解质量之比;也可以根据打气前后药液上方的气体温度和体积都相同,运用推论2,有.同样的,第(2)问也可以直接运用推论3,得.

类型2 抽气问题

例5(2020年山东卷)中医拔罐的物理原理是利用玻璃罐内外的气压差使罐吸附在人体穴位上,进而治疗某些疾病.常见拔罐有两种,如图2所示,左侧为火罐,下端开口;右侧为抽气拔罐,下端开口,上端留有抽气阀门.使用火罐时,先加热罐中气体,然后迅速按到皮肤上,自然降温后火罐内部气压低于外部大气压,使火罐紧紧吸附在皮肤上.抽气拔罐是先把罐体按在皮肤上,再通过抽气降低罐内气体压强.

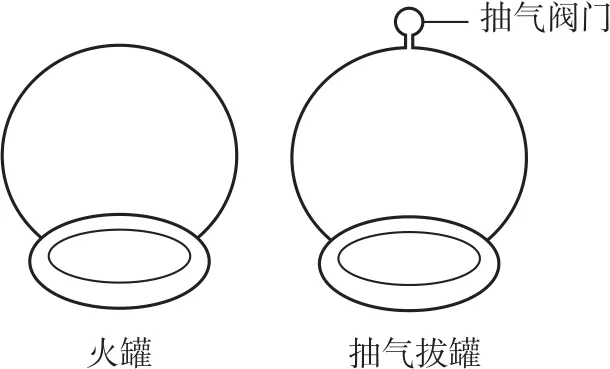
图2

某次使用火罐时,罐内气体初始压强与外部大气压相同,温度为450K,最终降到300K,因皮肤凸起,内部气体体积变为罐容积的.若换用抽气拔罐,抽气后罐内剩余气体体积变为抽气拔罐容积的,罐内气压与火罐降温后的内部气压相同.罐内气体均可视为理想气体,忽略抽气过程中气体温度的变化.求应抽出气体的质量与抽气前罐内气体质量的比值.

设外界大气压为p0,火罐的容积为V0,则火罐内气体初始状态的压强为p0,温度为T1＝450K,体积为V0;温度降低后气体的压强为p2,温度为T2＝300K,体积为.由理想气体状态方程得,代入数据得p2＝0.7p0.

本题首先运用推论1 的理想气体分态方程求解抽出气体的体积ΔV,然后根据抽气拔罐中抽出气体的压强和温度与抽气前气体的压强和温度相同,运用推论3求解质量之比.也可以根据抽气前后罐内气体的温度相同,运用推论2,求得剩余气体的质量与抽气前罐内气体质量之比,即.

类型3 灌气(气体分装)问题

例6甲、乙两个储气钢瓶储存有同种气体(可视为理想气体).甲瓶的容积V1＝8L,瓶中气体的压强为7p0;乙瓶的容积V2＝4L,瓶中气体的压强为p0.现通过细管将两瓶连通,甲给乙充气,直到两钢瓶中气体压强相等,充气过程中两瓶中气体温度相等且保持不变,细管中气体体积忽略不计.求稳定后:

(1)乙储气钢瓶中气体的压强p;

(2)甲瓶中气体的质量与甲瓶中原有气体的质量之比.

(1)由玻意耳定律有7p0V1＋p0V2＝p(V1＋V2),解得p＝5p0.

(2)若稳定后甲瓶中气体再被压缩到原来的压强7p0时,体积为V3,由玻意耳定律pV1＝7p0V3,设稳定后甲瓶中气体的质量与甲瓶中原有气体的质量之比为k,由密度的定义有,联立解得

本题第(1)问直接运用推论1的理想气体分态方程;第(2)问将甲瓶中稳定后的气体的压强和温度转换到与稳定前气体的压强和温度相同,运用推论3求解质量之比.也可以直接根据稳定前后甲瓶中气体的温度与体积相同,运用推论2,得k＝.

类型4 漏气问题

例7一位消防员在火灾现场发现一个容积为V0的废弃的氧气罐,经检测,内部封闭气体压强为1.2p0.为了消除安全隐患,消防员拟用下面两种处理方案:

(1)冷却法:经过合理冷却,使罐内气体温度降为27 ℃,此时气体压强降为p0,求氧气罐内气体原来的温度;

(2)放气法:保持罐内气体温度不变,缓慢地放出一部分气体,使罐内气体压强降为p0,求氧气罐内剩余气体的质量与原来总质量的比值.

(2)假设将放出的气体和剩余的气体都收集起来,等温转换到压强为p0的状态,其体积为V,由玻意耳定律有1.2p0V0＝p0V,解得V＝1.2V0,则剩余气体与原来气体的总质量之比为.

本题第(2)问也可以根据放气前后氧气罐内气体的体积和温度相同,运用推论2,得

3 小结

对于同种理想气体,其状态参量中的压强和温度属于强度量,不具有加和性,而体积属于广延量,但也只能在压强和温度相同的情况下具有加和性.因此,在解决状态转换和变质量问题时,需要灵活运用克拉珀龙方程及其推论,巧妙转换气体状态,以实现快速准确求解的目的.

(完)