基于长短期记忆网络的FRP 约束混凝土圆柱循环轴压应力-应变预测模型

姜克杰，胡 松，韩 强

(北京工业大学城市与工程安全减灾教育部重点实验室，北京工业大学，北京 100124)

FRP(Fiber Reinforced Polymer)作为一种纤维增强聚合物，因其轻质、高强、耐腐蚀、耐疲劳等优点而受到土木工程领域的广泛关注，近年来在土木工程领域得到了广泛的应用[1-2]。其中一个重要的应用方向是将其用于约束混凝土，使混凝土处于三向应力状态，从而显著提高其强度、韧性和延性[3]。近年来，越来越多的FRP 约束混凝土复合材料被开发和应用[4-7]。除了用于混凝土结构的加固，FRP 还被用于新建结构。

在实际应用中，为了保证FRP 约束混凝土柱设计的可靠性和经济性，有必要全面了解FRP 约束混凝土在单调轴压和循环轴压下的应力-应变特性。随着试验数据的累积以及机器学习技术的进步，基于知识的或数据驱动的建模范式引起了许多研究者的关注。与传统的基于力学原理的材料行为建模方法不同，基于知识的或数据驱动的建模范式为材料行为的预测提供了另一种途径。这种想法可以追溯到GHABOUSSI 等[8]的工作，他们使用神经网络对材料的力学行为建模。目前，这种建模范式现已被广泛应用于土木工程材料和构件的力学行为预测。数据驱动的建模方法能够自适应地从试验数据中学习材料的力学特性，学习到的力学规律被存储在神经网络的权重参数中。这在一定程度上克服了传统建模方法的不足，主要表现为：1)不依赖于专家经验和先验的模型假设，可以快速开发复杂的力学模型；2)建模能力通过“万能近似定理”[9]得到保证；3)具有很强的可扩展性和可维护性。

许多研究者采用ANN 方法对FRP 约束混凝土圆柱的抗压强度进行了预测[10-13]，结果表明：ANN 具有很强的非线性映射能力，预测精度均优于传统的数学模型。WU 等[14]基于RBF 神经网络对FRP 约束混凝土圆柱的抗压强度进行了预测。CASCARDI 等[15]基于ANN 对FRP 约束混凝土圆柱的约束有效性系数进行预测，进而得到抗压强度。NADERPOUR 等[16]采用ANN、遗传编程和GMDH 方法对FRP 约束钢筋混凝土圆柱的抗压强度进行了预测，并给出了简化的预测方程。遗传编程方法可以给出显式的表达式，因此也被用于预测FRP 约束混凝土圆柱的抗压强度[17-20]。除了ANN 外，逐步回归、模糊逻辑、自适应神经模糊推断系统、多变量自适应回归样条和M5 模型树也被用于对比[21-22]。此外，ELSANADEDY 等[23]和MANSOURI 等[22]采用ANN 对FRP 约束混凝土圆柱体抗压强度和极限应变进行了预测。除FRP 约束混凝土圆柱外，少量的研究者也对FRP 约束混凝土方柱/矩形柱的极限条件进行了预测[24-26]。张书颖等[27]提出了一种基于XGBoost 集成学习的FRP 加固混凝土梁抗弯承载力预测方法。最近，JIANG 等[28]建立了基于ANN 的FRP 约束混凝土的极限条件预测方法，并开发了具有递归结构的ANN 模型用于单调轴压下应力-应变全曲线的建模。

可以看到，数据驱动的建模方法在FRP 约束混凝土极限条件预测方面取得了长足的进展。然而，就作者们所知，在数据驱动的建模背景下，目前还没有针对FRP 约束混凝土的应力-应变全曲线建模进行过系统的研究，尤其是循环轴压下复杂的滞回行为。JIANG 等[28]仅对单调轴压下FRP约束混凝土的应力-应变全曲线进行了研究。然而，循环轴压下FRP 约束混凝土的应力-应变行为的建模需要考虑复杂的加卸载规则和荷载路径相关的记忆效应，因此更具挑战性。这促使研究者开发一种新的能够处理这种复杂行为的数据驱动的建模方法。

在数据驱动的材料或构件的全曲线力学行为建模领域已经发展了几种建模方法。LUO 等[29]提出了一种基于多输出支持向量机的骨架曲线模型ML-BCV，用于快速预测钢筋混凝土桥墩在弯曲、剪切以及弯剪破坏模式下往复循环加载的骨架曲线。ML-BCV 预测时考虑了桥墩的基本材料和几何特性、外部荷载和失效模式，但是仅能用于预测骨架曲线。HUANG 等[30]提出了一种基于ANN 的滞回力-位移模型ML-HLFD，用于表征具有不同特性的钢筋混凝土桥墩的侧向力和位移之间的关系。ML-HLFD 是一种两阶段的方法，模型输入与ML-BCV 类似，但模型的输出是传统滞回模型的参数，如Pinching4 模型。预测得到滞回模型的参数后，仍基于传统滞回模型进行计算。然而这种方法受到传统滞回模型建模假设和建模能力的约束，仅能提供不准确的滞回力-位移曲线。

近年来，深度学习方法在土木工程中的交叉应用领域取得了一些新的进展。例如，WU 等[31]基于深层卷积神经网络(CNN)对结构动力响应进行估计。XU 等[32]提出了一种基于长短期记忆神经网络的区域震害实时评估框架，许泽坤等[33]发展了类似的响应预测方法，并改进了模型的评价指标。最近，深度学习方法也被用于材料或构件的全曲线力学行为建模。WANG 等[34]提出了一种基于GRU 和混合注意力机制的材料模型深度学习框架UA-Seq2Seq，用于对具有历史依赖特性的响应进行预测。然而，他们使用传统的Teacher forcing 机制[35]训练模型，可能导致训练过程不稳定和不鲁棒的预测结果。XU 等[36]提出了一种两阶段的模拟复杂滞回行为的高级矫正训练策略，然而，两阶段的矫正训练策略也显著增加了训练过程的复杂度。与ML-HLFD 等模型不同，这些基于深度学习的建模方法能够以端到端的方式建模，且不对模型的行为施加先验约束，因此具有更强的灵活性。目前，针对此类模型在网络架构设计、训练策略以及模型的鲁棒性等方面的研究仍存在显著的提升空间。

本文提出了一种用于建模循环轴压下FRP 约束混凝土柱应力-应变特性的神经网络预测模型。主要贡献和创新性可以总结为以下几个方面：

1)提出采用长短期记忆(LSTM)单元和简化的注意力机制对循环应力-应变曲线中广泛存在的显著的滞后性和复杂的加卸载规则进行建模。所提模型的记忆能力来自三个方面，即输入中的历史信息、LSTM 隐层状态以及注意力机制提供的上下文向量。

2)将构件的物理参数有效地集成在网络的输入中，用于应力-应变曲线的条件生成。

3)提出采用相对损失函数训练模型，避免受到样本长度和幅值的影响，能够更加准确一致地描述模型的预测精度。

4)提出了数据裁剪和渐进训练机制用于提高模型训练稳定性和预测精度，并抑制曝光偏差问题。

该模型能以端到端的方式进行高效的训练且不依赖任何专家经验。通过一个FRP 约束普通混凝土柱的循环轴压数据库对所提模型的准确性和鲁棒性进行了充分的评估。该模型旨在为FRP 约束混凝土材料循环轴压模型的快速开发提供一种新的途径。其可以用于指导新型FRP 复合材料的研发和结构设计，也可以作为传统材料模型的替代。

1 方法论

循环荷载下应力-应变曲线(或力-位移曲线)中的滞回效应是循环材料模型建模的关键。这种滞回效应来自循环加载和卸载过程中试件中材料的累积损伤以及内部的耗能机制。此外，随着加卸载过程的进行往往还伴随有试件强度和刚度的退化。因此，滞回效应的本质是试件应力-应变响应的荷载时程依赖性。这种荷载时程依赖性要求在计算当前加卸载步的响应时，必须对试件经历的加卸载循环历史进行有效的回溯。这等价于要求神经网络应当具有某种记忆能力，记录试件曾经受到过的加卸载历程，从而判定系统在当前荷载步所处的状态并做出正确的预测。

然而，赋予神经网络记忆能力并不容易，尤其是长期记忆。传统的ANN 并不具备记忆能力，尽管ANN 可以拟合任意复杂的函数(f:A→B，对于集合A中的任何一个元素a，在集合B中都存在唯一的一个元素b与之对应)[9]。然而，循环轴压下的应力-应变曲线存在同一输入对应多个不同输出的情况。即，循环应力-应变曲线并不属于函数的范畴。JIANG 等[28]使用了一种具有反馈递归结构的ANN，手动地为ANN 网络赋予了简单的记忆能力。然而，这种简单的记忆能力对于建模复杂的循环应力-应变曲线并不是最优的。当加载时程较长时，可能需要长程记忆。受到深度学习中自然语言处理(NLP)领域对语言建模的启发[37-38]，本文使用长短期记忆(LSTM)单元[39]作为模型中的记忆部件，并采用注意力机制[40]增强模型的记忆能力。

1.1 循环神经网络RNN 和长短期记忆网络LSTM

循环神经网络(Recurrent Neural Network, RNN)是一种专门为时间序列建模设计的具有记忆能力的神经网络[41]，其结构具有循环本质。RNN 不仅能考虑当前时间步的输入，也能通过反馈连接考虑历史输入的影响。因此，循环轴压应力-应变曲线中的时程依赖性可以被充分地考虑。RNN 的计算图如图1 所示。假设输入序列为x=[x1,x2,···,xT],xi∈Rm，输出序列为y=[y1,y2,···,yT]，yi∈Rn。对于时间步t，RNN 中的计算过程可以表示为：

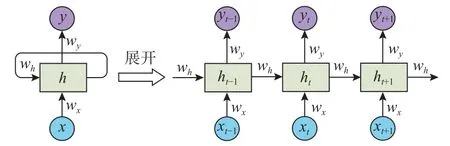
图1 单向 RNN 计算图及其展开结构Fig.1 Unidirectional RNN computation diagram and its expanded structure

式中：W和b为可学习的网络参数；Wx、Wh和Wy分别为输入变量xt、上一时间步的隐变量ht-1和当前时间步的隐变量ht的权重参数矩阵；bh和by称为偏置；ht-1和ht∈Rd为隐层状态向量(h0=0)；f为非线性激活函数。在每个时间步RNN 都使用一个全连接网络，即，普通的ANN。在不同的时间步，RNN 网络参数共享。从式(1)看出RNN 模拟了一个非线性的微分动力系统，并且理论上RNN能够以任意精度逼近任意一个非线性动力系统[42]。

从形式上看，式(1)和式(2)是传统的状态空间模型的非线性扩展。RNN 通过上一时间步的隐层状态ht-1考虑历史输入的影响。即，RNN 假定所有的加载历史信息均由ht-1表示。这种假定具有马尔科夫属性，这简化了模型的复杂度。然而，当加载时程序列较长时，受限于隐层状态向量ht-1的表示能力，模型会不可避免地遗忘过去输入的荷载信息。这种现象被称为“记忆饱和”。这导致RNN 仅具有短期的“记忆”能力，其对于循环轴压下应力-应变的建模是不利的。此外，在处理长时间序列时，RNN 的训练容易产生梯度消失和梯度爆炸等问题[43]。

目前，为了克服RNN 的长期依赖问题，一种主流的做法是引入精细的门控单元[37,39]，用于调节信息的流动。本文采用的LSTM (Long Short Term Memory)神经网络是目前最流行的网络结构之一。LSTM 神经网络是一种具有长时间记忆能力的网络，可以在一定程度上缓解长期依赖问题。图2给出了LSTM 网络计算图。图3 给出了常用的激活函数。LSTM cell 的计算图如图2(a)所示。LSTM 通过引入遗忘门、输入门和输出门，以及新的内部状态Ct获得捕捉长期依赖关系的能力。

图2 LSTM 网络计算图Fig.2 LSTM network calculation diagram

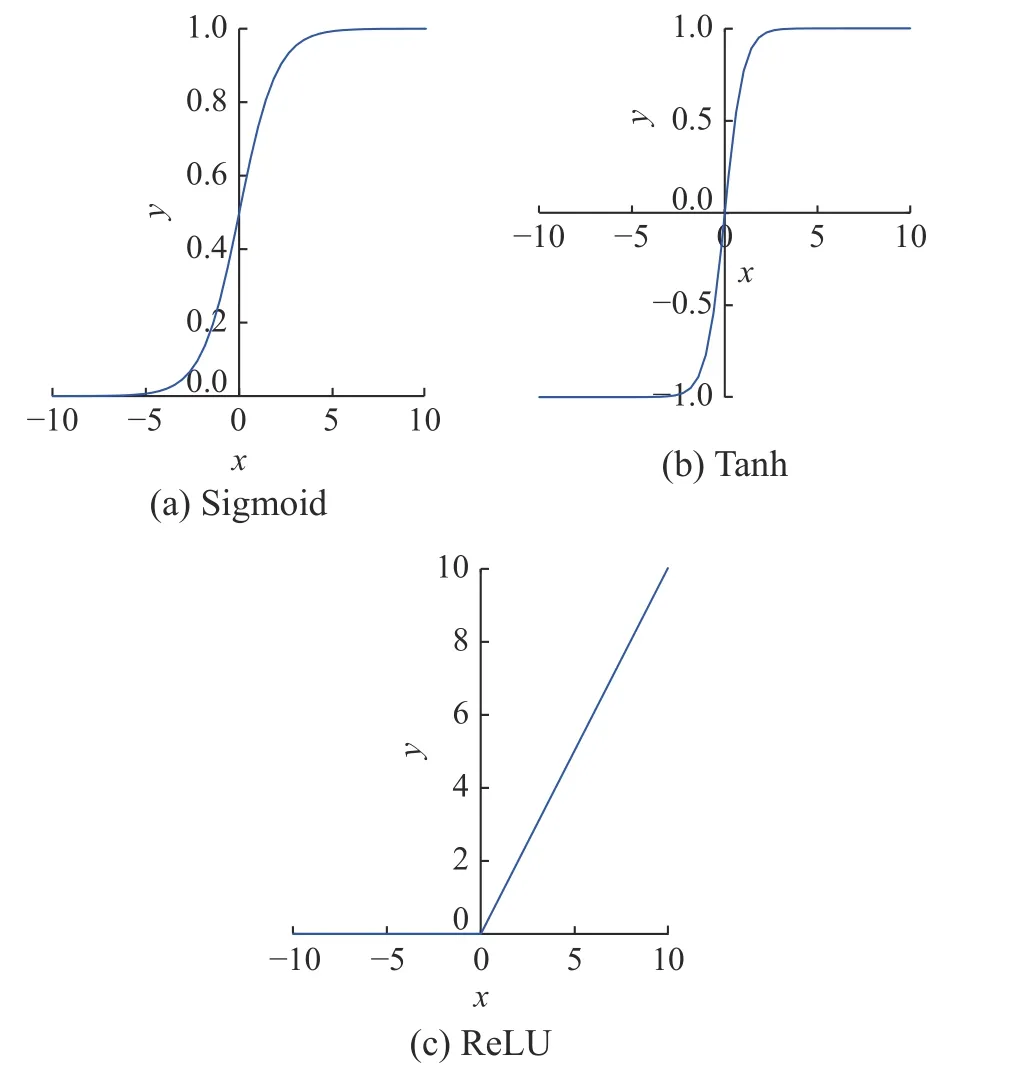
图3 激活函数Fig.3 Activation function

LSTM 单元内部的计算流程可以表述如下。

遗忘门可以计算为：

式中，σ(x)为Sigmoid 激活函数，输出介于0～1 之间，如图3(a)所示。为了表述的简洁性，这里以及下文等式中的W和b均为可学习的网络参数。

输入门计算为：

式中：it的计算使用了Sigmoid 激活函数；Ct的计算使用了Tanh(x)激活函数，如图3(b)所示。

下一步是基于遗忘门和输入门提取的信息执行对Ct状态的更新，计算如下：

式中： ⊗为逐元素相乘；ft⊗Ct-1为需要遗忘的信息；it⊗为需要增加的信息。

输出门计算为：

如图2(b)所示，这里ht有两个作用：一方面，ht将作为输入到下一个时间步的记忆变量；另一方面，ht将作为当前时间步的外部输出，其可以作为后续网络层的输入特征。例如，后续网络层可以是另一层LSTM 网络或ANN 输出层。对于后者可以计算为：

LSTM 网络层的展开结构如图2(b)所示。LSTM cell 与RNN 类似，具有首尾相连的反馈连接。区别在于LSTM cell 内部具有精细设计的门控机制。需要指出图2(b)中每个时间步的LSTM cell是同一个网络，即每个时间步LSTM cell 的网络参数是共享的。

1.2 基于LSTM 的循环轴压应力-应变模型

循环轴压应力-应变曲线的建模本质上可以看作是序列到序列(Seq2Seq)的映射问题。典型的输入-输出序列如图4 所示。

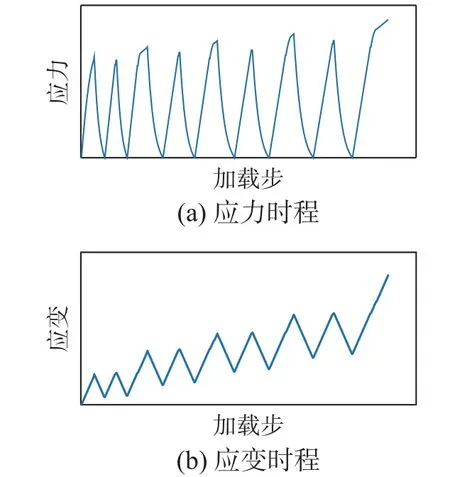
图4 典型的输入-输出序列Fig.4 A typical input-output sequence

建模的挑战在于输出对荷载路径的依赖性和复杂的加卸载规则，本文通过具有记忆能力的LSTM cell 进行建模。基于LSTM cell 和ANN 设计了FRP 约束混凝土的循环轴压应力-应变模型，如图5 所示，其具有Seq2Seq 网络架构[38]。该模型包括5 个部分，即输入、编码器、解码器、输出层和输出预测值。编码器和解码器均使用LSTM cell，负责对输入特征进行编码和翻译为抽象特征。输出层的ANN 最终将这些特征映射为输出预测值。

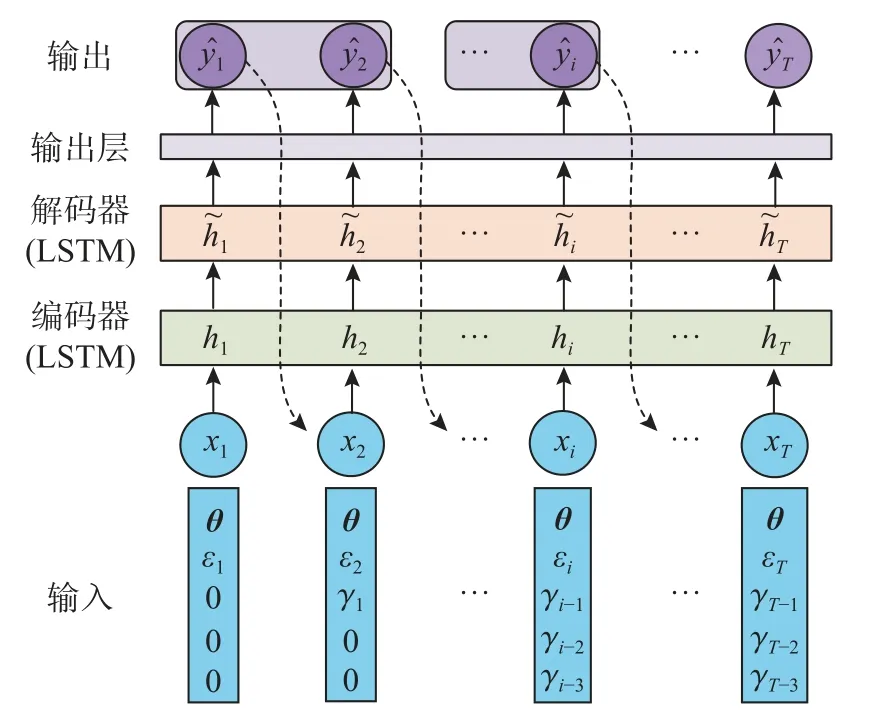
图5 模型架构Fig.5 Model Architecture

首先，对网络的输入进行了仔细设计。将输入序列记为x，输出序列记为y。模型可以为应变ε驱动或应力 σ驱动。这里以应变驱动为例进行说明。为了能够预测不同试件的力学行为，网络的输入必须有效整合试件的材料参数信息。此外，尽管LSTM cell 具有一定的记忆能力，仍有必要将最近的几个历史输入输出数据作为输入的一部分用于增强网络的建模能力和鲁棒性。因此，所提网络的输入由3 部分组成，分别为材料参数θ、当前时间步的应变输入值 εi以及最近的 λ个历史输入和输出值对γi=(εi,σi)。第i个时间步的输入表示为：

式中，材料参数θ为FRP 约束混凝土试件的基本几何和材料属性，表示为：

式中：D为约束混凝土核心的直径；H为试件高度；为非约束混凝土的峰值应力； εco为非约束混凝土的峰值应变；Ec为混凝土弹性模量；t为FRP 的总厚度；EFRP为FRP 的弹性模量；εh,rup为FRP 的环向断裂应变。除了以上材料的测量参数，还考虑了三个手工制作的特征用于增强预测性能，即刚度比 ρK、应变比 ρε和约束比，fl为约束应力的最大值(环向拉应力导致FRP 断裂时的围压)。这三个手工特征的具体计算方式与文献[28]保持一致。

尽管LSTM cell 自身已经具备卓越的记忆能力，发现网络输入中显式地包含最近几个历史时间步的输入输出信息 γi可以进一步改善预测效果。本文选取最近的 λ个时间步的历史输入-输出信息作为辅助特征：

需要指出，对于最初几个时间步的输入，可能还没有生成足够的历史信息用作输入。对于这种情况可以用0 值或固定的常量进行填充，如图5所示。最终，结合材料参数 θ 和 γ以及当前时间步的应变输入值 εi，网络的每个时间步共包含11+2λ+1个输入特征。

通常，在网络训练阶段式(14)中的历史值为真实的应力-应变值。而在测试阶段真实的应力-应变值将是不可访问的，因此他们将是网络的预测值，如式(15)所示。这种训练策略被称为“Teacher forcing”[35]，如图5 中的带箭头的虚线所示，这意味着，网络在训练时是开环的，而在测试阶段他们将转为具有输出反馈连接的闭环机制。尽管这种策略加速了网络训练，然而训练好的模型可能存在曝光偏差问题[44]。关于这种机制的讨论及影响将在后文给出。为了避免曝光偏差，本文提出渐进训练机制，并在训练和测试时均使用式(15)中的预测值。

对于编码器和解码器中的LSTM 层，可以采用一层或多个LSTM cell 层的堆叠。与普通的ANN 相比，深层的LSTM 网络并不容易训练。因此，并不建议使用过深的LSTM 层。如图5 所示，在每个时间步中，对于Encoder，输入特征xi将与LSTM 层中上一时间步的编码隐层状态(记忆信息)hi-1相融合。对于Decoder，输入hi将与上一时间步的解码隐层状态相融合。这些融合后的特征一方面作为当前时间步应力预测的特征，另一方面也作为记忆信息向后传递。关于LSTM层的层数以及隐层状态ht和Ct的维度将作为超参数在后文进行详细讨论。

输出层为简单的单层前馈神经网络[28]，如图6所示。输出层接收来自LSTM 层的融合特征，并负责将这些特征向量映射为最终的应力。式(11)描述了图6 中的计算过程。需要指出，输出层的权值在每个时间步中是共享的，即同一个输出网络在每个时间步被重复使用。

图6 单层前馈神经网络Fig.6 Single layer feedforward neural network

1.3 基于注意力机制的记忆力增强

图5 中的Seq2Seq 网络架构的主要缺陷在于用于存储记忆的隐层状态ht维度是固定的。随着序列的增长，ht的容量容易达到饱和。目前，一种有效的改进是引入一个额外的动态外部记忆状态，称之为上下文向量。注意力的关键思想在于，在获得t时间步的解码隐层状态后，将作为查询信息对之前所有的编码隐层状态信息HEn=[h1,h2,···,ht-1]进行检索。目前，存在两种典型的注意力机制，Bahdanau Attention[45]和Luong Attention[46]，主要区别在于解码层和注意力层的顺序以及注意力向量的计算方式。本文采用Luong Attention，计算图如图7 所示。

图7 注意力机制计算图Fig.7 Calculation diagram of attentional mechanism

注意力向量的计算流程简述如下：

步骤1：计算第t时间步的解码隐层状态∈Rd；

步骤2：基于计算HEn=[h1,h2,···,ht]∈Rd×t中每个历史编码向量的对齐得分(alignment scores)：

注意，本文使用dot 形式的模型计算对齐得分，其仅仅计算两个向量的内积(即相似性)，存在的其他模型参考GALASSI 等[40]的工作。

步骤3：基于对齐得分计算归一化的注意力权重(attention weights)：

步骤4：基于注意力权重 α对HEn加权求和得到上下文向量(context vector)：

可以看到上下文向量CV是HEn的凝缩，其提供了额外的动态记忆，并随着随时间步而变化。随后，将上下文向量与解码隐层状态拼接用于预测第t时间步的应力值。将式(11)改写为：

式中，激活函数ReLU(x)=max(0,x)，如图3(c)所示。注意，本文使用ReLU[47]约束应力输出为非负值。ReLU避免了Sigmoid激活函数在输出值接近1 时的梯度饱和问题(导致预测结果偏低)。

所提模型的整体计算流程如图8 所示。本文的建模过程可分为数据预处理、网络训练和模型评估、网络超参数优化三个部分，每个部分的细节将在下文详细阐述。

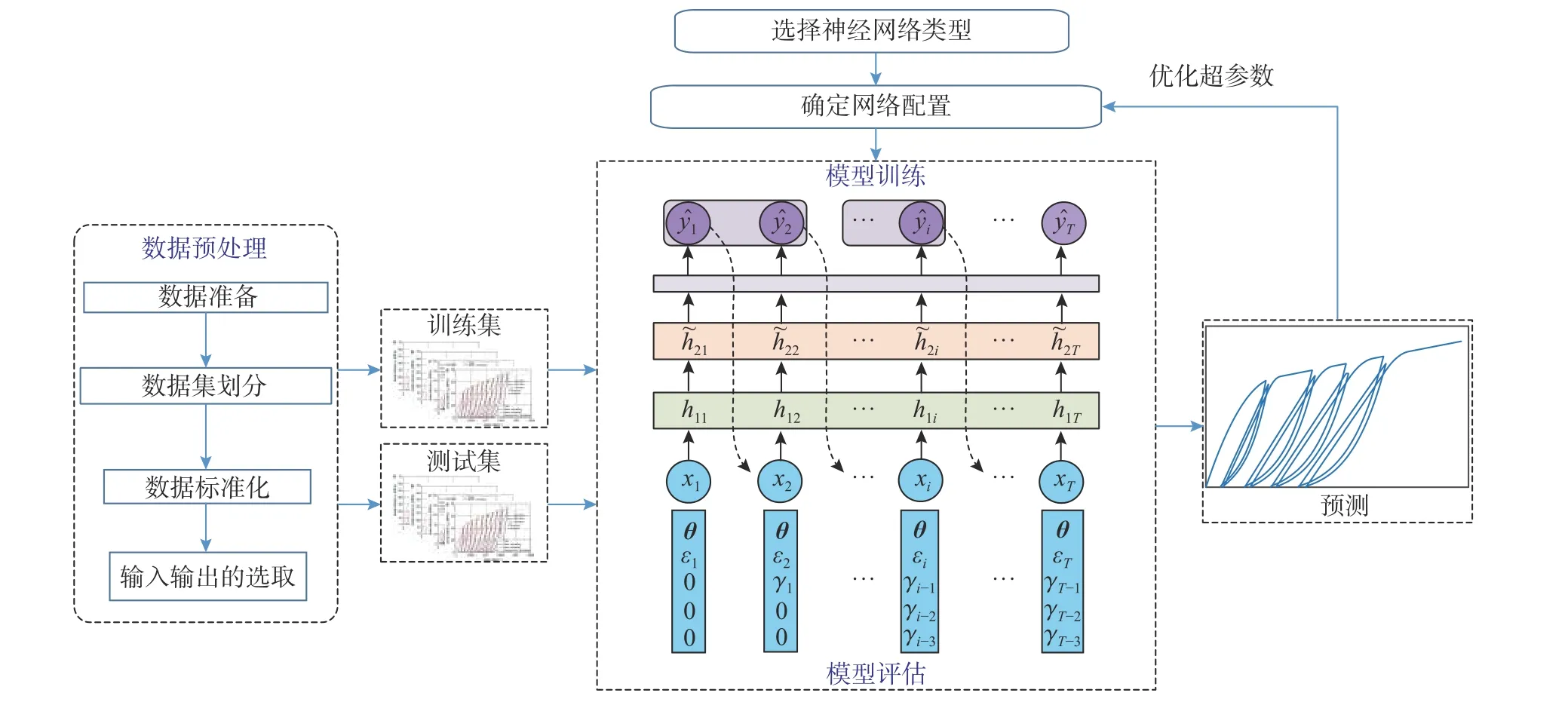
图8 整体建模框架和计算流程Fig.8 Overall modeling framework and calculation process

2 数据集的准备和预处理

2.1 数据集的准备

为了对所提模型的准确性和鲁棒性进行充分的评估，制作了一个包含166 个FRP 约束普通混凝土柱的循环轴压数据库，试件的具体参数参考文献[28]。由于模拟精度的原因，原始数据库中的28 号、29 号和103 号样本未参与计算。数据库中试件直径D的范围为100 mm～200 mm，非约束混凝土的强度范围为26.2 MPa～55.2 MPa，约束比的范围为0.0169～0.994。包含的FRP 类型包括CFRP、高模量CFRP、GFRP、E-glass FRP和AFRP。本文采用LAM 和TENG[3]的模型作为基准模型。对166 个FRP 约束普通混凝土柱的应力-应变响应进行了模拟。这些数据随后被用于所提神经材料模型的训练和测试。

数据集使用的加载路径如图9 所示。图9(a)给出了几个典型的加载路径。不同试件每级的加载水平大致相同，并卸载至应力为零。这导致不同试件的卸载点基本相同，再加载点不同。每级循环2 次～3 次。数据集中使用的随机加载路径如图9(b)所示。应变增量步长设为10-5，考虑到计算的精度和训练成本，将生成的数据下采样为原来的1/10。在实际应用中，相同的分析精度下，不同的加载路径会导致不同长度的响应序列，这意味着测试序列和训练序列的长度可能是不同的。然而，所提模型使用的LSTM 单元具有处理任意长度序列的能力。因此，测试序列的长度没有必要与训练集相同。

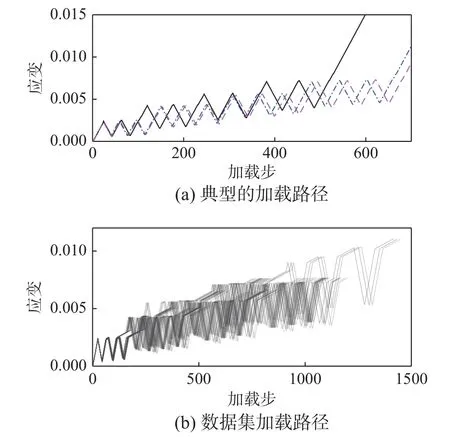
图9 加载路径Fig.9 Loading paths

2.2 数据的预处理

如式(12)所示，模型的输入分为两个部分，即试件参数和应力-应变历史。这些输入特征在尺度上可能存在显著差异，如FRP 的厚度和试件的高度不在同一个数量级。这导致输入中不同维度的特征具有不同的权重。输入特征的这种量级差异将会给模型的优化带来困难，同时也会降低模型的精度。实际上，神经网络模型真正需要学习的是输入-输出之间的变化模式，而跟特征的绝对幅值无关。因此，在训练模型之前有必要对输入特征进行归一化处理[48]。在机器学习中，常用的数据归一化方法有最大-最小归一化和z-score 归一化两种。

最大-最小归一化采用式(20)将输入中每个维度的特征分别缩放至[0, 1]区间：

式中：x为缩放前的特征；xs为缩放后的特征；max(x) 和min(x)分别为训练集中特征x的最大值和最小值。注意，不同特征的缩放是独立进行的。

z-score 归一化方法将数据集缩放为均值为0，方差为1 的高斯化数据：

式中，mean(x) 和std(x)分别为训练集中特征x的均值和标准差。

试件参数采用z-score 归一化方法进行处理，而应力-应变时程采用最大-最小归一化。本文数据的归一化采用scikit-learn[49]。预处理模块中的MinMaxScaler 和StandardScaler 完成。将归一化后的数据集用于模型的训练和测试。

2.3 数据集增广和渐进训练机制

受限于试验成本，对于材料本构模型的开发，通常仅能访问较少的试验数据。此外，通过初步评估发现当应力-应变序列非常长时，序列模型收敛缓慢，而且预测精度不佳。为克服以上两点困难，本文为神经材料模型的训练提出了一种新的训练机制，即模型的渐进训练。将数据集中的每个应力-应变曲线序列均匀(或随机)裁剪为K份，表示为[(ε1,σ1),(ε2,σ2),···,(εK,σK)]。然后将分割后的序列以递增的方式拼接起来，[[(ε1,σ1)],[(ε1,σ1),(ε2,σ2)],···,[(ε1,σ1),(ε2,σ2),···,(εK,σK)]]。这至少提供了两方面的好处：一方面序列长度以递增的方式呈现，学习的难度也是递增的，更容易学习的短序列对网络起到稳定和引导的作用；另一方面，数据裁剪后由于样本量增多应力-应变曲线的每个部分被网络更频繁的访问，这显著提高了信息的利用率。本文采用均匀裁剪的方式，K=20。经验结果表明：所提出的数据增广和渐进训练机制显著加快了模型的收敛速度，提高了预测精度。

3 网络的训练

本文采用开源神经网络计算框架PyTorch 1.9[50]构建图5 所示的网络模型。采用基于误差反向传播的mini 批随机梯度下降算法对网络进行训练。该方法每次从训练集中随机选取(不放回抽样)一批样本作为输入，批尺寸为N。网络同时对一批样本的响应进行迭代预测，计算是并行的。然后，计算预测值和真实值之间的误差，并通过反向传播算法对网络参数进行更新。本文将批尺寸N设为1。采用平均相对误差(MRE)作为序列预测值和真实值y之间误差的度量：

式中：yij为第i个样本的第j个应力值；Li为第i个样本的长度。需要注意，不同样本通常具有不同的序列长度Li。此外，数据增广中使用的随机裁剪也使训练样本的长度之间非常不同。因此，本文推荐使用相对损失MRE，其为各个变长样本的预测精度提供了更为客观的评价。

具体地，网络优化算法采用Adam 算法[51]，该算法是一种基于一阶梯度信息的随机目标函数优化算法。学习率(LR)是神经网络训练过程中另一个重要的超参数，它决定了参数更新的速度。当学习率过大时，可能会跳过局部最小值点；当学习率过小时，会消耗过多的迭代时间。本文的初始学习率设置为0.001。由于Adam 算法是一种自适应学习率的算法，训练过程中每个参数的学习率会根据一阶和二阶动量自适应地调整。本文中，Adam 一阶矩估计和二阶矩估计的指数衰减率β1和 β2分别为0.9 和0.999。此外，还利用指数型学习率衰减来改善模型的收敛性。学习率随训练的轮次(Epoch)呈指数型衰减，LRE=0.001·γE。本文衰减指数γ=0.98。

由于本文使用的数据集规模较小，模型可能发生过拟合。为了避免过拟合，采用早停机制来控制模型的训练程度[28]。如图10 所示，如果网络训练在第n个轮次达到最小测试误差，并且从第n个轮次开始连续p个轮次不刷新最小测试误差，则训练停止并将第n个轮次的模型作为最优训练模型。其中，p称为耐心值，本文p=30。这种早停机制可以有效地避免网络发生过拟合。

图10 早停机制Fig.10 Early stop mechanism

4 结果与讨论

4.1 超参数影响及最优网络配置

首先对网络的超参数进行了研究，以期找到合适的网络参数配置并评估网络性能对超参数选取的敏感性。本文编码器和解码器中LSTM 层数均取1 层，经验结果表明这对当前的建模任务是足够的。对于更复杂的材料行为可能需要更深的网络。LSTM 中的隐层状态向量ht和Ct使用了相同的维度。编码器和解码器中的隐层状态向量ht和维度也是相同的。研究了隐层状态向量的维度以及输入中考虑的历史时间步长对预测性能的影响。隐层状态向量的维度分别取16、32 和64，如表1所示。输入中考虑的历史时间步长 λ分别取1、10和20，如表2 所示。每个配置下网络的总参数也列于表中。

表1 对 LSTM 隐层状态维度的分析Table 1 Analysis of LSTM hidden layer state dimension

表2 对输入中历史时间步长λ 的分析Table 2 Analysis of the historical time step λ in the input

随机选取80%(133 个)的样本作为训练集，剩余20%(33 个)的样本用于模型性能测试。采用所提方法进行数据增广后训练集和测试集分别包含2660 个和660 个样本。由于增广后训练集具有充足的样本，将轮次最大值设为50。模型的评估指标采用式(22)中的MRE，其中N等于训练集或测试集样本总数。计算机配置为Intel(R) Core(TM)i7-10700KF CPU @ 3.80 GHz GPU Nvidia GeForce GTX 1080。50 个轮次的训练大约需要25 h。

不同网络配置下的训练曲线如图11 所示。可以看到在经过1 个轮次后不同网络配置下的测试集误差通常低于10%，表明网络能够迅速收敛。这得益于所使用的数据增广和渐进训练机制。在经过50 个轮次后，网络基本收敛。最终的训练集和测试集精度列于表1 和表2 中。图11(a)表明三种隐层状态维度下的测试集性能接近，且网络均没有发生过拟合。随着隐层状态维度的增加，模型性能略有提升。图11(b)表明输入中包含的历史时间步的数目对网络的收敛速度有显著影响，然而，其对最终的测试集精度仅有轻微的影响。这可能得益于注意力机制，当输入中的历史时间步长较小时，网络的记忆能力会更多地求助于上下文向量CV中的历史信息。以上分析表明，所提模型的性能对LSTM 隐层状态维度和的历史时间步长取值较为鲁棒。采用Case 3 作为最优配置用于后续的分析。

4.2 网络泛化性能评估

图12 给出了最优配置下的网络对测试集样本循环性能的预测结果。限于篇幅，这里仅展示部分样本，其余样本具有一致的精度。所示应力-应变曲线是经过归一化的。应变归一化系数为0.0111，应力归一化系数为73.0351 MPa。可以看到预测应力值与真实应力值匹配良好。需要强调，测试集样本的参数配置与训练集样本不同，其对于训练好的网络而言是从未见到过的新样本。可以看到不同的试件具有显著不同的循环力学行为，例如刚度、屈服点、循环包络曲线以及卸载和再加载段的演化等。结果表明：网络已经学到了不同参数FRP 约束混凝土试件在循环轴压下的应力-应变规律，并给出了相当可信的预测。

图12 测试集样本预测精度Fig.12 Test set sample prediction accuracy

图13 进一步检查了网络对渐进展开的测试样本的预测性能，渐进展开的测试样本与训练网络时使用的增广数据集中的训练样本类似。可以看到，网络对不同渐进展开状态下的样本具有一致的预测精度。此外，结果也证明了训练好的网络能够处理不同长度的测试样本。图13 也演示了在所提渐进训练机制下网络对同一应力-应变值的重复访问，这显著提高了对应力-应变曲线不同部位的信息利用率。本文发现这种渐进训练机制能够显著提高过渡段的预测精度。这可以解释为，相对于循环段，过渡段的数据非常稀疏，经过数据裁剪，过渡段数据能够更频繁地被网络访问和学习。

图13 测试集样本的渐进展开Fig.13 Progressive expansion of test set samples

图14 检查了预测曲线与真实曲线之间累积耗能的差异。时间步的累积耗能定义为在地震工程中，该指标经常被用于评估结构的耗能能力和抗震性能。这里采用该指标评估模型的累积预测误差。图14 表明随着加载的进行，模型的累积预测误差保持在可控范围内。这意味着训练好的网络不存在显著的曝光偏差问题，这对于模拟长持时的应力-应变响应至关重要。

图14 累积耗能对比Fig.14 Cumulative energy consumption comparison

图15 进一步考察了测试集预测误差的统计特性。图15(a)给出了增广后的测试集中所有样本MRE的分布。对完整长度(未裁剪)样本的预测误差进行了单独的标记。可以看到，大部分测试样本的MRE 小于1%。此外，完整长度样本的预测误差与裁剪后的长度较短的样本的误差非常接近，这再次验证了模型的累积预测误差保持在可控范围内。图15(b)给出了测试集中所有样本每个应力点预测误差的分布，其接近正态分布。注意，这里应力均经过了归一化。第4.2 节已经提到应力归一化系数为73.0351 MPa。测试集最大应力预测误差为73.0351×0.013 ≈0.95 MPa。注意，裁剪后的样本最大应力值远小于73.0351 MPa，因此这里仅统计具有完整长度样本的预测误差。图15 中预测误差的统计特性为模型预测性能提供了统计上的保证。

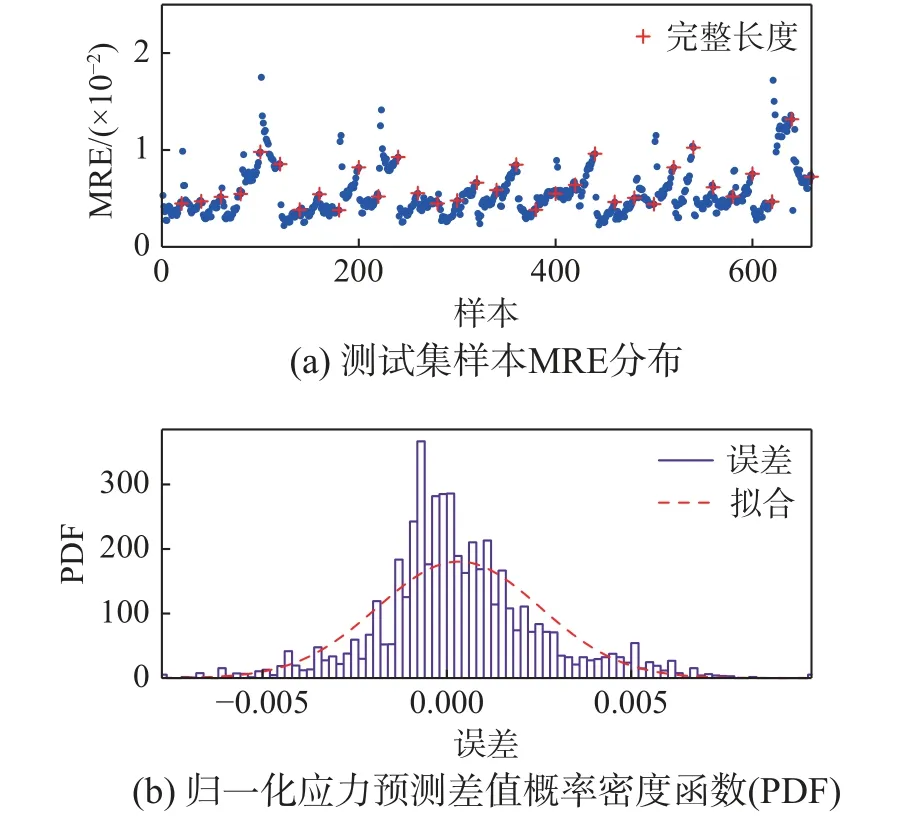
图15 测试集样本预测误差的统计特性Fig.15 Statistical characteristics of sample prediction errors in test sets

4.3 渐进训练机制的影响

本节进一步讨论了数据增广和渐进训练机制对模型收敛速度和预测精度的影响。这里考察了均匀步长(记为Case 6)和非均匀步长(记为Case 7)两种情况。在模拟数据的某些时间节点，如历史卸载点附近的过渡段，有时需要减小加载步长用于获得更精细的模拟结果，这导致了不均匀的步长。这里所有工况均采用与Case 3 相同的网络配置。图16 对比了三种工况下的训练曲线，可以清楚地看到使用数据增广和渐进训练机制的Case 3，网络的收敛速度和预测精度要比其余两个工况高一个数量级，而Case 6 和Case 7 的精度类似。这充分证明了渐进训练机制的有效性。表3 中给出了每隔10 个轮次的训练集和测试集MRE 精度，Case 6 和Case 7 的最终测试集误差分别是Case 3的8.1 倍和5.3 倍。

表3 渐进训练机制对收敛速度和预测精度的影响Table 3 Effect of progressive training mechanism on convergence rate and prediction accuracy

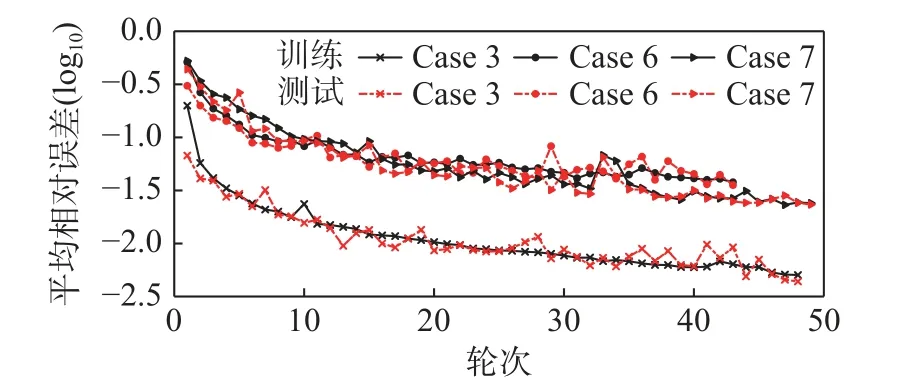
图16 渐进训练机制对模型收敛速度的影响Fig.16 Effect of progressive training mechanism on model convergence rate

图17 检查了Case 6 和Case 7 的典型预测结果。从图17 中可以看到，不使用渐进训练机制的预测结果往往给出较差的局部预测精度，尤其是骨架曲线部分出现明显的偏差和抖动。此外，注意到Case 7 中进行步长切换时引起预测值明显的抖动。这些不鲁棒的预测结果在Case 3 中均未出现，这些结果进一步证明了使用渐进训练机制的必要性。

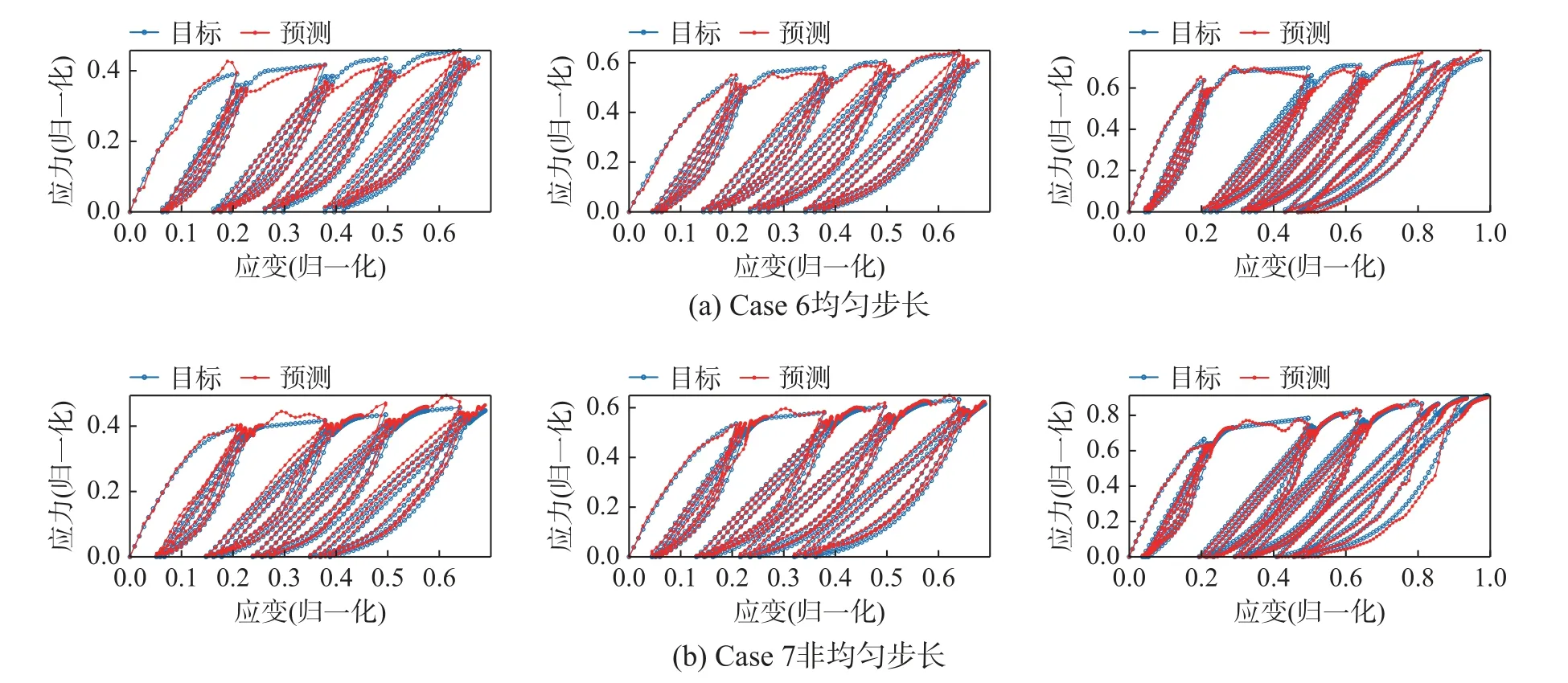
图17 不使用渐进训练机制的预测结果Fig.17 Prediction results without using the progressive training mechanism

5 Teacher forcing 与Exposure Bias

Teacher forcing 机制[35]以一定的概率使用真实的历史输出值，其经常被用于稳定和加快Seq2Seq模型的训练。对于循环网络，在训练初期，网络的预测能力较弱，这导致前期较差的预测值将显著影响后续的预测值。Teacher forcing 策略由于使用了真实值的引导，因此能够显著加快网络的训练。然而，与之伴随的问题是训练好的模型可能存在所谓的“曝光偏差”(Exposure Bias)问题[44]。鉴于潜在的曝光偏差效应，使用Teacher forcing 机制时应当仔细评估模型在测试集上的预测精度。对不同曝光偏差效应消除机制的讨论和对比超出了本文的研究范围，这将留给以后的工作。

考虑到Teacher forcing 机制可能带来曝光偏差，本文没有使用Teacher forcing 策略，而是采用了渐进训练机制对数据进行增广。结果表明所提渐进训练机制能够很好地稳定并加快网络的收敛。对当前模型预测结果的检查并没有发现显著的曝光偏差效应。因此，提出的渐进训练机制可作为Teacher forcing 训练机制的一种有效替代。

6 结论

本文提出了一种新型的FRP 约束混凝土循环轴压应力应变预测框架，该框架将具有非线性滞回属性的材料力学系统的建模转化为序列到序列的映射问题。材料循环本构建模的挑战在于输出对荷载路径的依赖性，这要求神经网络具有记忆能力。本文采用带有注意力机制的Seq2Seq 框架对材料的循环本构规律进行学习。所提模型具有卓越的记忆能力，可以有效地整合历史输入对当前输出的影响。提出了渐进训练的概念，并用于数据集增广和稳定训练，减小了网络训练难度，加速了网络的收敛。通过一个包含166 个FRP 约束普通混凝土柱的循环轴压数据库，证明了该框架建模精度和有效性。该框架为FRP 约束混凝土循环轴压模型的快速开发提供了一种新的途径。主要的发现和结论总结如下：

(1) 所提模型的记忆能力来自三个方面，即输入中的历史信息、LSTM 隐层状态以及注意力机制提供的上下文向量，三者之间相互影响。

(2) 输入中显式地包含历史输入输出信息能够显著加快模型的收敛，尽管最终的精度相差不多。

(3) 所提数据增广和渐进训练机制稳定并显著加速了网络的训练，而且没有观察到显著的曝光偏差问题，对于非均匀计算步长也能给出鲁棒的预测。因此，渐进训练机制可作为Teacher forcing训练机制的一种有效替代。对测试集预测误差的统计分析证明了所提框架的高性能建模能力。

(4) 结果表明：所提出的模型对LSTM 隐层状态维度的选取较为鲁棒。随着LSTM 隐层状态维度的增加，测试集精度略有增长。

初步的研究表明该方法是一种有前景的计算框架，未来将在试验数据库上进行验证，并考虑更复杂的FRP 约束方形、矩形截面的循环轴压应力-应变关系的建模，以及考虑下降段的情况。此外，与现有的建模方法的对比工作也将在未来开展，以充分评估不同建模技术的优劣。