考虑渗透各向异性的隧道周围饱和软土固结特性分析

龚昭祺，林廷松，李文乾，胡安峰

（1.浙江大学 工程师学院，浙江 杭州 310015；2.杭州市建设工程质量安全监督总站，浙江 杭州 310005；3.中国中铁十局集团城市轨道交通工程有限公司，广东 广州 511400；4.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058）

0 引 言

近年来，国内地铁盾构隧道建设里程日益增长，由于盾构隧道常由管片拼接而成，且存在注浆孔洞，在隧道结构不均匀沉降、列车荷载等因素的影响下盾构管片常有局部透水通道。同时，地面为一天然的透水通道，因此，在地下水丰富的地区由盾构施工引起的隧道周围软土中的超静孔压会逐渐消散，从而引起土体发生固结与沉降。

目前，关于隧道周围软土固结问题的研究方法主要有解析法、数值模拟法和试验法。在解析法方面，詹美礼等[1]将衬砌排水条件简化为完全排水以及完全不排水，用Merchant三元件线性流变模型考虑了土体流变性，使用复变函数得到了隧道周围土体超孔压及固结沉降解答；刘干斌等[2-3]针对饱和黏弹性土体中深埋隧道的固结问题，考虑土体流变、衬砌渗透及其刚度的影响，应用Biot固结理论获得了相应的固结及衬砌-土体相互作用解析解；黄明华等[4]采用分数阶黏弹性模型对洞周超静孔隙水压力消散问题进行了求解。但以上研究均未考虑软土在固结过程中渗透性与压缩性的非线性变化，曹奕[5]采用与詹美礼等[1]相同的求解方法，引入e-lgk和e-lgσ′关系，但所得解析解是在假设土体自重沿深度均匀分布、渗透性与压缩性同步变化的情况下得到的，并且可求解域有一定的局限[6]。数值模拟法方面，张冬梅等[7]考虑盾构隧道局部渗透性及软土时效性，研究了衬砌渗流特性对地表长期沉降发展的影响规律；WONGSAROJ等[8]针对重超固结伦敦黏土中的单个露天隧道长期固结沉降进行了一系列有限元分析，针对隧道几何形状、地面条件和衬砌渗透系数进行了参数研究；陈相宇等[9]以长沙南湖路江底盾构隧道工程为例，采用ABAQUS软件建立三维流固耦合有限元模型，研究了土体在不同渗透性条件下地层注浆加固对土体孔隙水压力的扰动影响规律；ZHANG等[10]以武汉地铁2号线为例，采用PFC离散元软件建立二维数值模型，研究强降雨诱发洪水造成的跨河隧道地层高水压对既有盾构隧道变形、内力及土层变形的影响。试验法方面，一些学者对盾构施工引起的隧道周围超静孔压进行了测量分析[11-13]。但以上研究均未综合考虑软土固结的非线性特性、软土渗透各向异性和隧道渗漏模式等因素影响下的隧道周围软土固结特性。因此，本文基于渗透系数和有效应力随孔隙比变化的非线性模型，引入二维固结控制偏微分方程，并利用一种交替隐式差分法对方程进行了求解，获得了在不同透水模式下隧道周围全场域软土的非线性固结解答，研究了软土渗透各向异性、软土厚度和初始有效固结应力对固结性状的影响规律。

1 二维非线性固结控制方程

考虑厚度为H，宽度为2B的软土模型，隧道中心位于水平中线且上方软土厚度为h处。计算简图如图1所示。地表排水，地基左右两侧及底部不排水，隧道衬砌视透水模式考虑均匀渗漏、局部渗漏和均匀+局部渗漏3种情况。

图1 计算简图Fig.1 Computing model

1.1 基本假定

（1）隧道纵向尺寸远大于横向尺寸，满足平面应变条件；（2）土体饱和，土颗粒和孔隙水不可压缩；（3）变形为小变形；（4）地基中各点土体所承受的竖向总应力不随时间变化；（5）地基内各点土体自由变形，不考虑成拱作用；（6）孔隙水流动服从Darcy定律，土体中渗流为正交各向异性。

1.2 基本方程

由土单元体内水量的变化率等于土体积变化率，可得基本控制方程为：

式中：γw为水的重度；ks为土体渗透系数；u为超静孔压；εv为土体体积应变；t为固结时间。

土体的压缩性和渗透性服从如下规律[14-15]：

式中：e为孔隙比；0e为初始孔隙比；Cc为压缩指数；σ'为有效应力；0σ'为初始有效应力；Ck为渗透指数；ks0为初始渗透系数。

通常将水平渗透系数kh与竖向渗透系数kv之比定义为kr，可得二维非线性渗流固结控制方程：

1.3 定解条件

（1）u(x, 0,t)= 0和u|透水孔=0（地表和隧道局部渗漏情况下的透水孔）；

（4）u(x,y, 0)=u0。

条件（3）中，κ为衬砌与土体的相对渗透性系数，定义为κ=kl/ ［ksr2ln(r2/r1)］，r1和r2分别为隧道内外半径，kl为隧道衬砌渗透系数[16]。条件（4）中的u0为初始超静孔压，可根据文献中现有数据进行拟合[11]。

2 方程数值求解

式（4）为二阶非线性偏微分方程，且由于所研究问题的区域为复连通域，难以获得严格意义上的解析解。有限差分法作为一种以数学方法为基础并依靠计算机进行求解的计算物理方法，在非线性问题求解中得到了广泛应用，故考虑采用有限差分法进行求解。考虑到有限差分的格式特点，本文采用一种交替隐式差分格式。网格划分如图2所示。

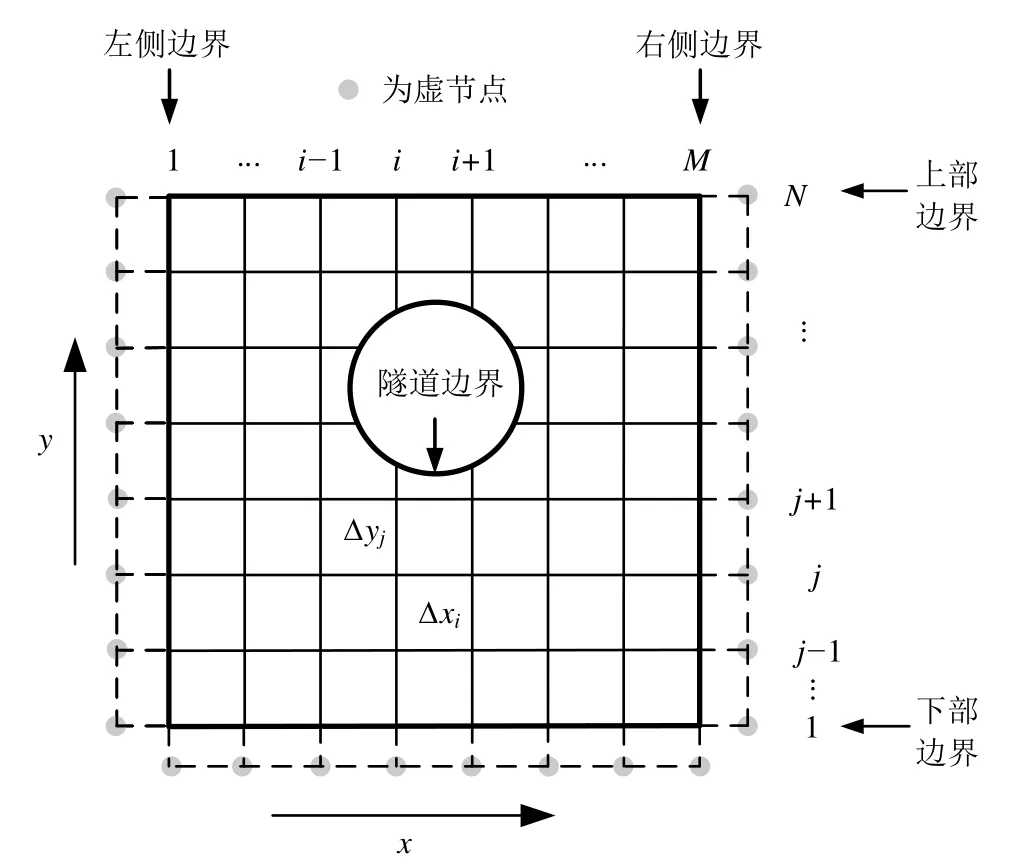
图2 网格划分图Fig.2 Schematic diagram of mesh division

不透水边界的计算通过构造虚节点的方法进行处理[17]，透水边界条件以及半透水边界的计算按相应公式进行处理。计算流程图省略。

式中：δ为中心差分算子，为土体初始固结系数，τ为时间步长，Δh为空间步长。

在求得任意时刻整个场域上的超静孔压的数值解后，平均固结度按定义即可求解。按超静孔压计算平均固结度：

式中：si,j=ΔxiΔyj，为离散点(xi,yj)处空间步长所围面积。

3 算例分析

3.1 差分退化解与解析解对比验证

隧道几何参数与物理参数如表1所示[5]。BERRY等[18]研究发现Cc/Ck范围大多为0.5～1.0，结合表1中Cc取0.25，故取Ck= 0.25。当不考虑软土固结过程的非线性以及渗透各向异性时，式（4）退化为Terzaghi-Rendulic固结控制方程，与文献[5]描述问题完全相同。将本文差分退化解与文献[5]中的算例进行对比验证，如图3所示。由图3可知，本文方法所得解与现有解析解基本一致，说明了本文差分退化解的正确性。

表1 隧道几何参数和物理参数Table 1 Geometric and physical parameters of tunnel

图3 本文差分退化解与既有解析解对比Fig.3 Comparison between degenerate solution and existing analytical solution

3.2 隧道透水模式对固结性状的影响

由于盾构管片的结构特性，管片在长期使用下因列车荷载、土体压力和接头老化等因素的影响难免会形成局部透水通道，因此，有必要对盾构管片透水的真实情况进行模拟，进而研究其对固结性状的影响。考虑到管片之间存在6个接头，故本节考虑将盾构管片渗漏局部透水通道简化为沿管片圆周向分布的6个完全透水点（见图4）。同时，由于盾构隧道结构在纵向由一环环的管片拼接而成，不妨将环缝看作均匀透水体。综上，本节将局部渗漏情况下的固结度与均匀透水情况进行对比分析。

管片渗漏形式对固结性状的影响如图5所示，由图5可见，局部渗漏情况下隧道周围软土固结度与均匀渗漏情况下差别较大，最大差值为17%，同时，综合考虑局部渗漏和均匀渗漏情况下的固结度与单独考虑局部渗漏情况下相差较大，所以，考虑局部渗漏情况十分重要。另外，虽然渗漏形式对固结过程有重要影响，但其对完全固结所需时间影响较小。

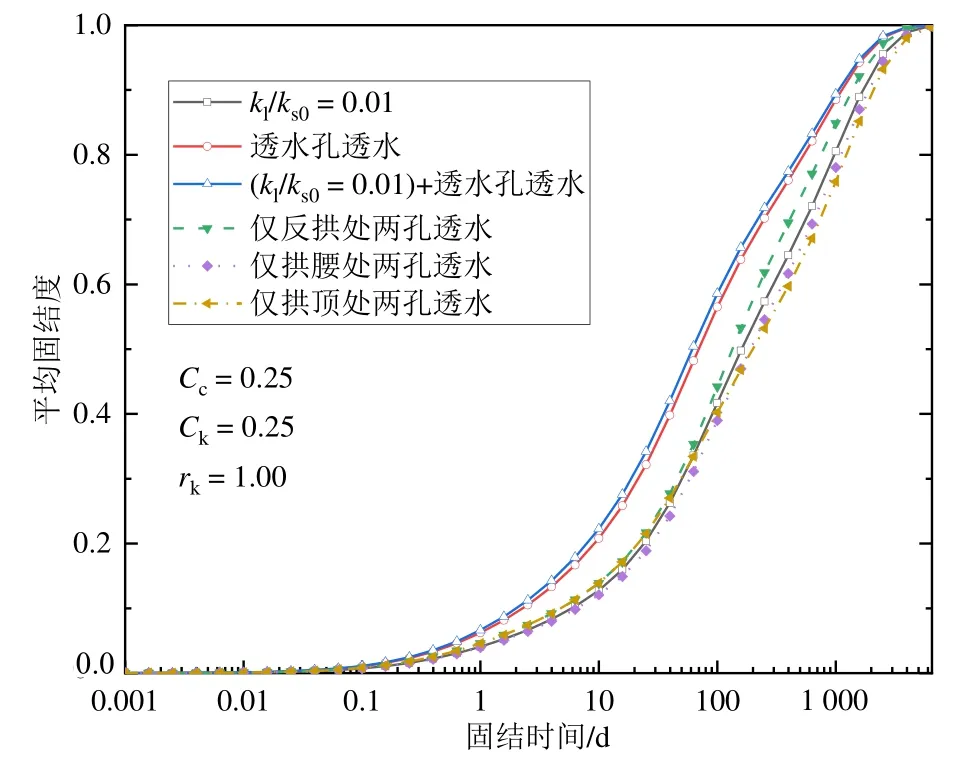
图5 管片渗漏形式对固结性状的影响Fig.5 Influence of segment leakage form on consolidation

渗漏形式对超静孔压分布的影响如图6所示，由图6可见，不同渗漏形式下隧道周围超静孔压分布完全不同，因此，若在渗漏情况下考虑因孔压扩散引起的有效应力分布进而研究隧道变形、土体竖向位移或其他相关问题时，渗漏形式的模式不可忽视，必须结合实际情况来进行分析研究。

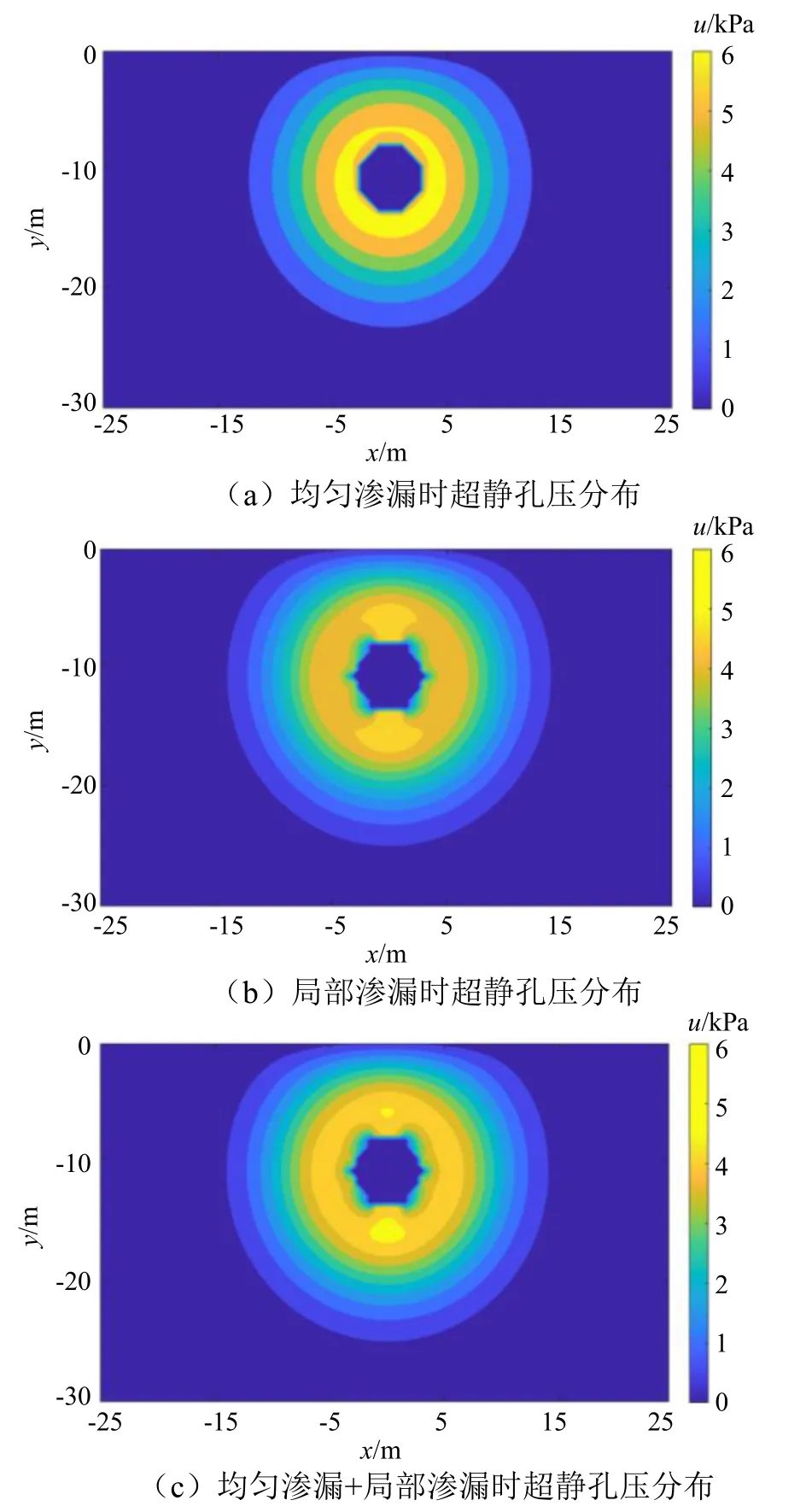
图6 渗漏形式对超静孔压分布的影响Fig.6 Influence of leakage form on excess pore water pressure distribution

3.3 土体渗透各向异性对固结性状的影响

对杭州原状土进行试验发现kr为1.1～1.4[19]，有学者提出只有将土体渗透的各向异性考虑在内才能准确模拟实际工况[20-21]，由此可见，渗透各向异性在滨海软土中较为明显，有必要研究渗透各向异性对隧道周围软土固结的影响。

图7为土体渗透各向异性对固结性状的影响，由图7可见，在结构性软土中各向异性的影响较为明显，固结速率随渗透各向异性的增大而增大。当kr足够大时（如填埋体kr最大为10[22]），渗透各向异性的影响必须予以足够重视。

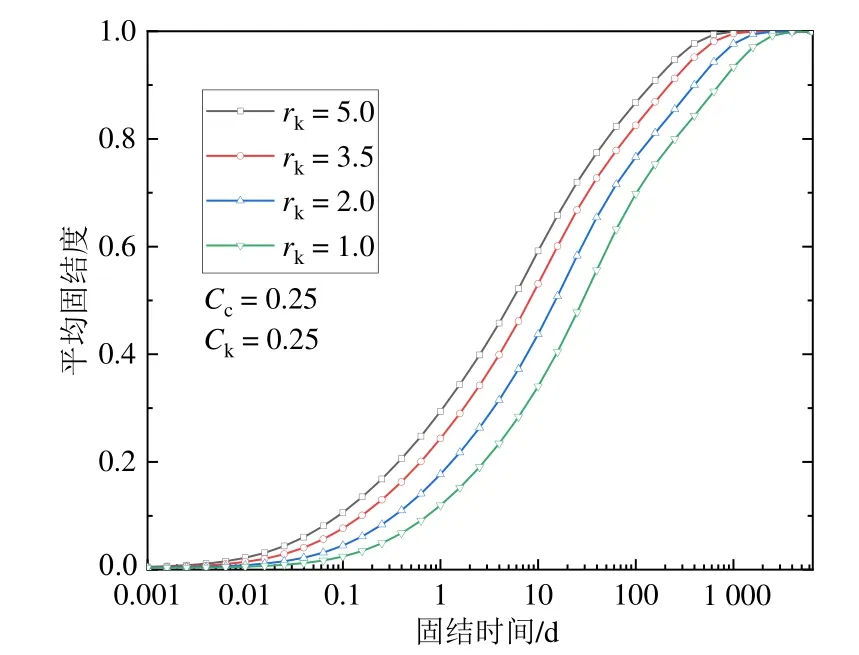
图7 土体渗透各向异性对固结性状的影响Fig.7 Influence of soil permeability anisotropy on consolidation

3.4 软土厚度对固结性状的影响

软土厚度对固结性状的影响如图8所示，由图8可见，软土厚度分别为20 m、30 m和40 m时，前60 d固结曲线重合，60 d后的一段时间内固结度差值越来越大。产生此现象的原因可能为：隧道作为一个透水边界，在固结前期，超静孔压消散基本仅发生在隧道边界处，软土厚度不影响其周围超静孔压的消散，同时，地基表面因其透水能力造成的超静孔压消散基本忽略不计。随着时间增长，孔压扩散至深层软土中，但地基底部不透水，由此造成了深厚软土中超静孔压消散较慢。

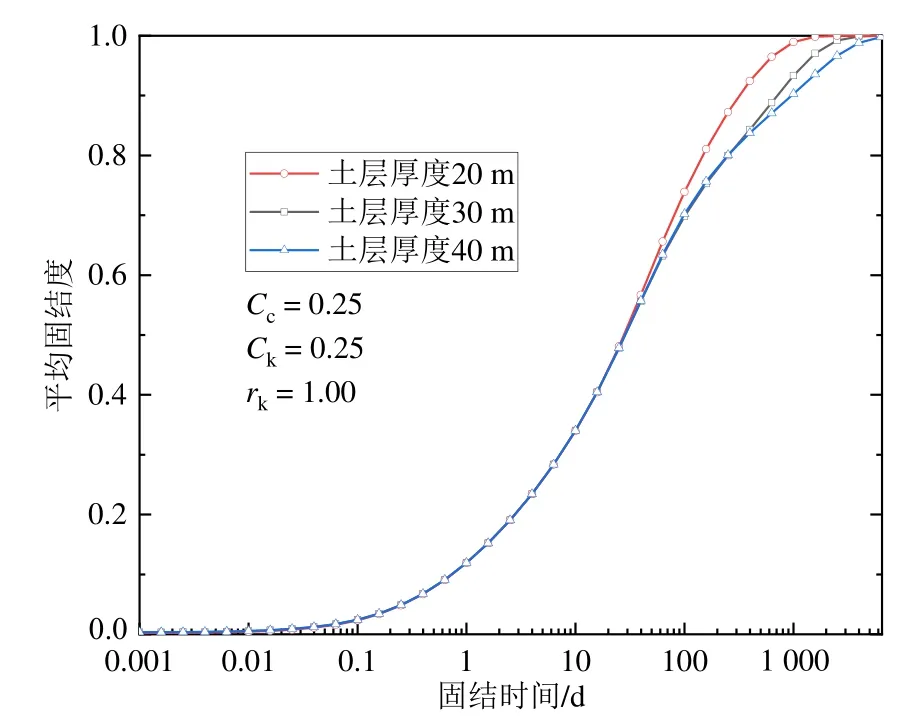
图8 软土厚度对固结性状的影响Fig.8 Influence of soft soil thickness on consolidation

3.5 初始有效固结应力对固结性状的影响

图9为假设初始渗透系数为一定值时不同初始有效固结应力 0σ'对固结性状的影响，由图9可知，相同时间内平均固结度随初始有效固结应力的增大而增大。这是因为土体初始有效固结应力随深度的增大而增大，若土体深度增加而渗透系数相同，则说明该地基整体渗透系数更大，因此固结速率更大。

图9 初始有效固结应力对固结性状的影响Fig.9 Influence of initial effective consolidation stress on consolidation

4 结 论

引入e-lgk、e-lgσ′模型，考虑软土因结构性造成的渗透各向异性，建立了隧道周围渗透各向异性饱和土体二维非线性固结控制方程。运用有限差分法对控制方程进行求解，研究了不同因素影响下的隧道周围土体固结发展规律，得到如下结论：

（1）盾构管片渗漏模式对隧道周围土体固结度以及应力场分布具有重要影响，应尽可能考虑实际情况。

（2）固结速率随渗透各向异性系数kr的增大而增大，当kr足够大时，必须考虑其对固结的影响。

（3）在固结前期，固结速率与软土厚度基本无关；在固结后期，固结速率随软土厚度的增大而减小。

（4）对于初始有效固结应力不同而初始渗透系数相同的各土体而言，固结速率随初始有效固结应力的增大而增大。