基坑开挖空间效应对邻近隧道的影响分析

余忠祥，过 锦

（1.杭州滨江房产集团股份有限公司，浙江 杭州 310016；2.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058）

0 引 言

近年来，为缓解城市人口快速增长带来的交通拥堵问题，城市轨道交通建设步伐逐渐加快，其中城市地铁的发展速度尤为显著。轨道交通周边因其较大的商业附加价值，往往适配商场、住宅等建筑的建设，因此，紧邻地铁施工的基坑工程案例越来越多。基坑工程土方开挖的卸荷会引起周边土体的水平位移，从而对隧道的水平位移及内力产生影响，严重时甚至引起隧道管片开裂渗水的情况。国内外相关案例已有不少：台北某基坑[1]开挖导致邻近地铁隧道结构受损，隧道管片出现了较大的裂缝；宁波某基坑[2]开挖致其邻近隧道管片渗水，对地铁隧道的安全运营产生了不利影响。为保证地铁隧道的安全运行，必须严格控制隧道的水平位移，相关规范也制定了地铁隧道的变形控制标准[3]。为确保工程的顺利进行，不至于因隧道变形过大而导致工程施工中断，需要在基坑开挖前对隧道变形进行评估，从而可以根据评估结果制定相应的控制方案，因此分析基坑开挖对邻近隧道的影响有其重要的实际意义。

目前，预估基坑开挖对隧道的影响主要通过理论研究、数值分析、模型试验及工程实测等方法。在数值模拟方面，由于基坑开挖的空间效应较为显著[4]，三维有限元分析越来越广泛地应用于基坑开挖环境影响方面的研究，黄宏伟等[5]及SHI等[6]均采用三维有限元软件研究了基坑开挖对邻近隧道水平位移的影响。在室内试验方面，HUANG等[7]及NG等[8]利用离心机分别分析了软土地基及砂土地基基坑开挖时邻近隧道的变形响应。实际工程案例在国内外也有较多研究学者进行了统计分析[9-12]，在此基础之上，刘波等[13]根据众多统计案例分析得到了预测隧道变形的经验公式。理论解析方法主要采用两阶段法：第一阶段，计算基坑开挖引起的附加应力；第二阶段，将隧道简化为长梁，长梁上作用第一阶段计算得到的附加应力，从而得到隧道的受力响应。因理论方法原理清晰，计算耗时少，也有不少学者进行了有意义的研究：张治国等[14]将隧道视为Winkler地基上的弹性地基梁，利用Galerkin方法求解微分方程得到了隧道变形的解析解；应宏伟等[15]考虑隧道的埋深效应，采用有限差分法得到了邻近既有隧道纵向变形表达式；LIANG等[16]采用铁木辛柯（Timoshenko）梁模型模拟隧道以考虑隧道的剪切效应，推导了隧道在邻近基坑开挖条件下的求解方法。张治国等[14]、徐日庆等[17]考虑基坑开挖的空间效应，分析了坑内土体开挖引起三面围护墙及坑底土体卸荷对邻近隧道的影响，但是卸荷的计算方法并未结合围护墙的变形，而土体性质、围护结构整体刚度及围护墙插入深度等都将影响卸荷的大小。另外由于坑内土体的挖除，卸荷无法通过坑内向坑外传递。总而言之，现有基坑开挖对邻近既有隧道影响的理论研究中鲜有文献考虑基坑开挖的空间效应，大多基于围护墙变形符合平面应变条件的假定。此外基坑卸荷也未结合围护墙变形，不能反映基坑实际的变形特性，因此有必要考虑基坑变形的空间效应，并进一步分析基坑变形对邻近既有隧道的影响。

本文考虑基坑变形的空间效应，基于围护墙空间变形曲面表达式，采用影像源法得到了围护墙变形诱发的坑外土体变形的三维位移场的分布，实现了将基坑开挖引起的坑外土体三维卸荷与围护墙曲面变形相结合。考虑隧道管片间的剪切效应，将隧道设为搁置于Winkler地基上的Timoshenko梁，采用两阶段分析法，将附加荷载施加于邻近既有隧道，提出了基坑开挖引起的邻近隧道水平变形的理论解析方法。

在本文方法推导过程中，为简化计算，主要有以下假设：（1）地基土体为各向同性的均质半无限连续弹性体，且不可压缩；（2）隧道与地基土体紧密连接，不发生脱离；（3）不考虑隧道既有变形及隧道与地基土体相互作用的时间效应；（4）计算第一阶段基坑开挖引起的土体附加应力时不考虑隧道存在的影响。

1 围护墙侧向变形空间分布

基坑开挖的空间效应不仅体现在围护墙变形沿深度方向不断地变化，同时体现在沿基坑边方向不断地变化，如图1所示，因此，围护墙变形会随着不同的空间位置而变化。木林隆等[18]考虑围护墙插入深度的影响，改进了张陈蓉等[19]的围护墙沿深度方向的变形公式，并结合围护墙沿墙方向侧向变形的表达式，提出了围护墙侧向变形曲面表达式如下（坐标原点O位于地表面基坑边中点，x轴正方向垂直于围护墙指向坑外，z轴正方向垂直于地表向下，y轴正方向由右手法则确定）：

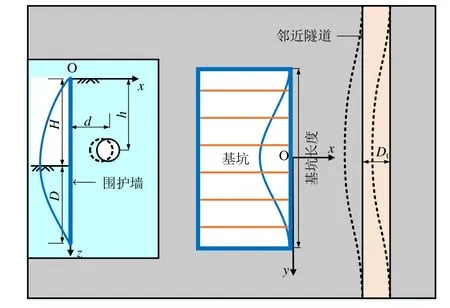
图1 围护墙变形示意图Fig.1 Schematic diagram of deformation of retaining wall

式中：fmax为围护墙最大变形；Hmax为围护墙最大变形处深度；H为基坑开挖深度；D为围护墙插入深度；L为围护墙长度。fmax和Hmax可根据工程所处的不同阶段采用支护结构的设计计算值或实测值进行分析。

2 围护墙变形诱发的坑外土体自由位移场

影像源法首先由SAGASETA[20]提出，用于求解弹性半空间内任意点土体损失或增加诱发周边土体位移场的解析方法，如打桩、隧道掘进等。由于基坑开挖后不符合土体处于无限半空间的条件，因此无法直接应用影像源法，XU等[21]以围护墙为镜面作镜像处理使得土体满足无限半空间的条件（见图2），随后得到了基坑变形符合平面应变条件下坑外土体侧向变形的表达式。本文基于此思路，分析得到了坑外土体侧向变形的三维位移场分布。

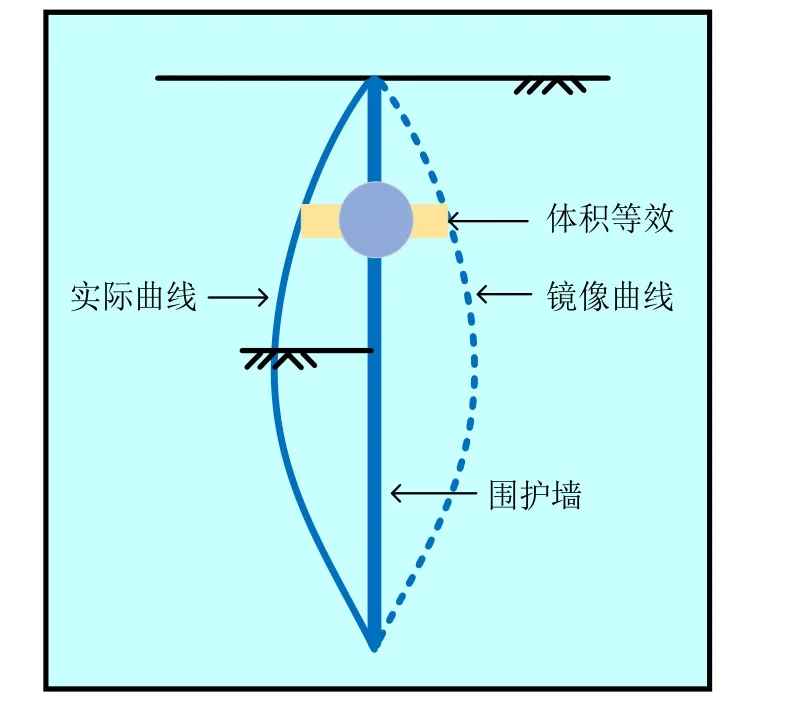
图2 镜像变换Fig.2 Mirror transformation

在三维空间下，影像源法孔隙收缩引起周边土体三维位移场求解步骤如下：

（1）沿地表面作镜像变化将土体扩展为无限空间，此时，孔隙收缩将会在地表面处产生应力，为消除地表面处的法向应力，在其镜像位置虚设一等大的膨胀孔隙，如图3（a）所示。

图3 影像源法求解步骤Fig.3 Steps of virtual image method

（2）为消除地表面上的切应力，在地表面上施加反向等大的切应力。此时，地表面上无应力存在。

叠加以上两步即可还原成实际应力状态，即如图3（b）所示应力状态，实际状态的土体位移即为以上两步位移之和。

求解步骤如下：设收缩孔隙球心位于C（0,y0,z0）处，半径为a，土体收缩径向位移为Sr，则收缩及膨胀孔隙在P1（x1,y1,z1）处土体x方向位移Sx1i及z方向位移Sz1i为：

地表面处产生的切应力可由弹性力学求解：

式中：G为土体剪切模量；γzx为剪应变。同理可求得：

将切应力τzx及τzy反向施加于地表，引起的水平位移Sx2i及Sx3i可由Cerruti问题位移解[22]求得，分别为：

利用体积等效将孔隙收缩体积围护墙变形建立关系：

则由围护墙变形引起坑外P1（1x,1y,1z）处土体x方向的水平位移为：

3 隧道水平向附加变形计算方法

将隧道简化为Timoshenko梁模型，其上受到附加荷载σt，且隧道置于Winkler地基上，则有微分平衡方程如下：

式中：(κGA)eq及 (EI)eq分别为隧道的等效剪切刚度及等效抗弯刚度；w(y)为隧道x方向水平变形；k为地基反力系数；Dt为隧道直径；Sx为前文计算得到的土体x方向水平位移。

将隧道均分为n段，并在两端各虚设2个节点，共计n+5个节点，每段长度为l。将式（13）改写为有限差分形式：

式中：wi为第i节点隧道x方向水平变形；iq为第i节点所受荷载。

结合边界条件，若隧道长度较基坑开挖长度更长，则隧道两端可视为自由，可知两端剪力及弯矩为0；若隧道端部连接有刚度相对较大的建（构）筑物，可视为固端，则端部转角及变形为0。在两端自由条件下：

求解式（15）得到w-2、w-1、wn+1、wn+2的表达式，代入式（14）并写成矩阵形式：

式中：K1为隧道位移刚度矩阵；K2为隧道剪切刚度矩阵；K3为隧道抗弯刚度矩阵；w为隧道位移列向量；P1为附加荷载列向量；P2为荷载修正列向量；P3为求解补充列向量。各矩阵表达式如下：

4 相关参数确定

隧道接头会显著降低隧道纵向的抗弯刚度，因此需要对隧道纵向抗弯刚度进行折减。志波由纪夫等[23]提出采用折减系数Kf来表示隧道接头对隧道纵向抗弯刚度的影响，纵向抗弯刚度折减计算方法如下：

式中：φ为中性轴位置；Ec为管片弹性模量；Ic为管片惯性矩；Ac为管片截面积；nt为螺栓数量；kb为接头螺栓的平均线刚度，kb=EbAb/lb，Eb为螺栓弹性模量，Ab为螺栓截面积，lb为螺栓长度；ls为环宽。

WU等[24]提出了隧道等效剪切刚度的计算方法，如下：

式中：ξ为隧道等效剪切刚度修正系数，本文取1；κb与κc分别为螺栓与管片环的剪切系数，对于圆形截面螺栓，κb取0.9，对于环形隧道管片环结构，κc取0.5；Gb与Gc分别为螺栓剪切刚度及隧道管片剪切刚度，Gb=Eb/2(1 +νb)，Gc=Ec/2(1 +νc)，νb与νc为螺栓和隧道的泊松比。

YU等[25]考虑埋深的影响提出了埋深影响下地基反力系数的表达式：

式中：Es为土体弹性模量；h为隧道轴线埋深；η为埋深影响系数。

5 算例验证

对上海某邻近隧道基坑[26]进行了开挖，基坑长度L约为70 m，开挖深度H为10 m，围护墙插入深度D为12 m，根据文献[27]计算结果，围护墙最大变形fmax取24 mm，发生位置Hmax约为10 m。邻近隧道距基坑边距离d为10.3 m，隧道轴线埋深h为10.1 m。上海隧道典型设计参数见表1，由此得到隧道纵向等效弯曲刚度(EI)eq为7.8×104MN·m2，隧道等效剪切刚度(κGA)eq为2.5×103MN。地基土弹性模量Es取2倍压缩模量为12.4 MPa，泊松比为0.35。

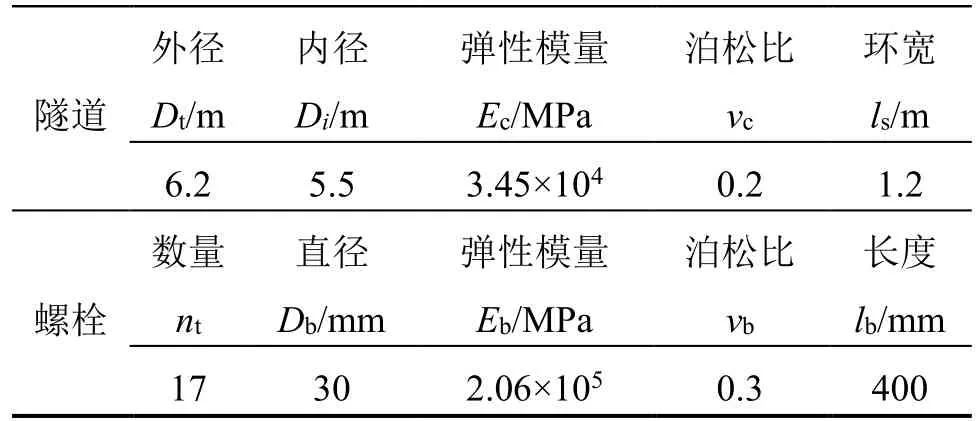
表1 隧道典型设计参数Table 1 Typical design parameters of tunnel

计算及实测数据对比曲线如图4所示，本文方法与实测数据的对比可见，计算方法在变形趋势上与实测数据取得了较好的一致性，在围护墙中部变形较为一致，在基坑角点处计算结果稍偏小，计算的变形最大值较实测数据也更为接近。总体来说，本文计算方法在预测基坑开挖引起邻近隧道变形的最大值及趋势上都具有一定的可靠性及适用性。

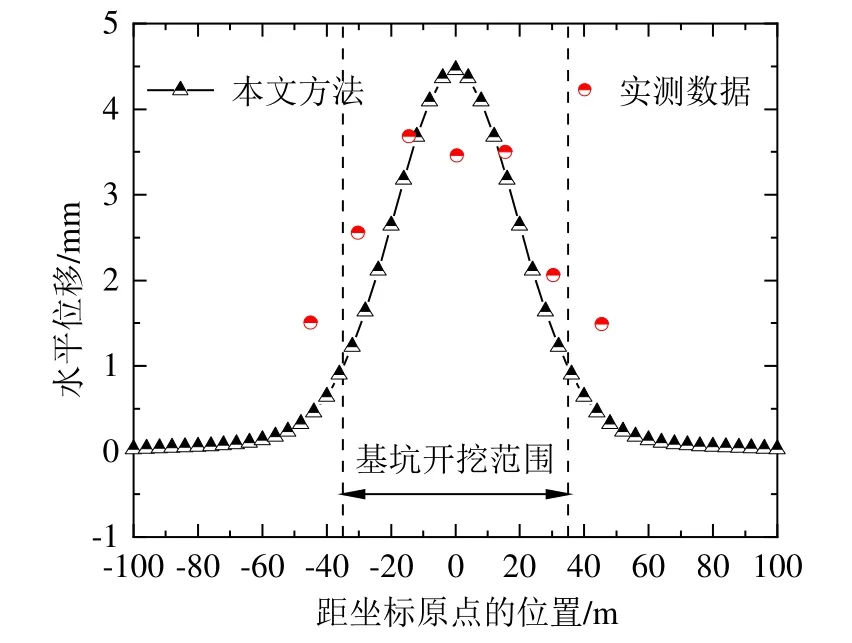
图4 计算及实测数据对比曲线Fig.4 Comparison curve of calculated and measured data

6 参数分析

本节建立一个基本算例，各参数取值如下：基坑开挖深度H为12 m，围护墙插入深度D为12 m，基坑长度L为100 m，围护墙最大变形fmax为35 mm，发生位置Hmax为12 m，地基土弹性模量Es为12 MPa，泊松比为0.3，隧道轴线埋深为12 m，距基坑边距离为8 m，隧道纵向等效弯曲刚度(EI)eq为7.8×104MN·m2，隧道等效剪切刚度(κGA)eq为2.5×103MN，隧道计算长度取200 m。进一步研究分析了隧道与基坑边距离、隧道埋深及围护墙最大变形等参数对邻近隧道水平位移、弯矩及剪力的影响。

6.1 隧道与基坑边距离的影响

图5～7分别为不同隧道与基坑边距离下隧道的水平位移、弯矩及剪力曲线。其中，隧道与基坑边距离选取了6 m、8 m、10 m、12 m、14 m。由图5～7可见，隧道水平位移、弯矩及剪力随着与基坑边距离的增加而逐渐减小。图5显示，隧道与基坑边距离为6 m时，隧道最大水平位移为13.6 mm，当距离增加2 m，隧道最大水平位移为10.5 mm，变形减小约23%；隧道与基坑边距离为12 m时，隧道最大水平位移为6.7 mm，当距离增加2 m，隧道最大水平位移为5.6 mm，变形减小约16%，表明距离的增加使得隧道变形减小的速率逐渐减小。图6显示，隧道与基坑边距离为 6 m时，隧道最大弯矩为2.2 MN·m，当距离增加2 m，隧道最大弯矩为1.6 MN·m，弯矩减小约27%；隧道与基坑边距离为12 m时，隧道最大弯矩为0.9 MN·m，当距离增加2 m，隧道最大弯矩为0.7 MN·m，弯矩减小约22%。图7显示，在基坑中部隧道剪力为0 kN，隧道与基坑边距离为6 m时，剪力最大值为142 kN，隧道与基坑边距离为14 m时，剪力最大值为40 kN，距离增加8 m，剪力减小了72%。

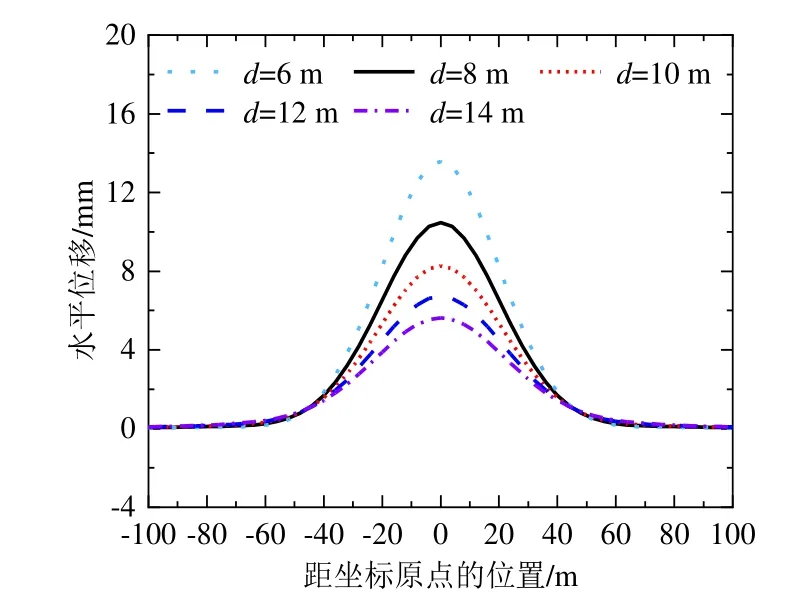
图5 不同隧道与基坑边距离下隧道水平位移曲线Fig.5 Lateral deformation of the tunnel with different distances between tunnel and foundation pit

图6 不同隧道与基坑边距离下隧道弯矩曲线Fig.6 Bending moment of the tunnel with different distances between tunnel and foundation pit

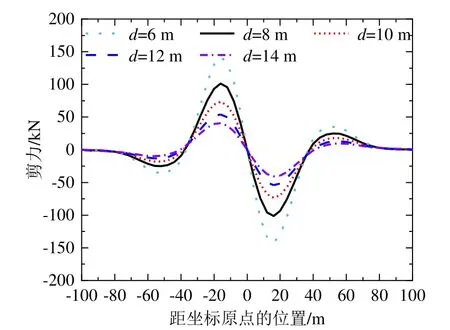
图7 不同隧道与基坑边距离下隧道剪力曲线Fig.7 Shearing force of the tunnel with different distances between tunnel and foundation pit

6.2 隧道埋深的影响

图8～10分别为不同隧道埋深下隧道的水平位移、弯矩及剪力曲线。其中，隧道埋深选取了4 m、8 m、12 m、16 m、20 m。由图8～10可见，隧道埋深在围护墙最大变形深度位置时，隧道的水平位移、弯矩及剪力都是最大的，因此，控制围护墙最大变形深度位置远离隧道埋深可以有效降低基坑开挖对邻近隧道的影响。图8～9显示，在隧道埋深为8 m及16 m时，距离围护墙最大变形深度位置都为4 m，变形及弯矩都较为接近，但埋深4 m时的隧道最大变形为8.4 mm，埋深20 m时的隧道最大变形为7.0 mm，表明隧道埋深与围护墙最大变形深度位置距离相等，但埋深较浅时，隧道变形受到基坑开挖的影响更大，但弯矩受到的影响较小。同样地，图10结果表明，隧道埋深处于围护墙最大变形深度处时剪力最大，隧道埋深与围护墙最大变形深度位置距离相等时，剪力大小较为接近。

图8 不同隧道埋深下隧道水平位移曲线Fig.8 Lateral deformation of the tunnel with different burial depths

图9 不同隧道埋深下隧道弯矩曲线Fig.9 Bending moment of the tunnel with different burial depths

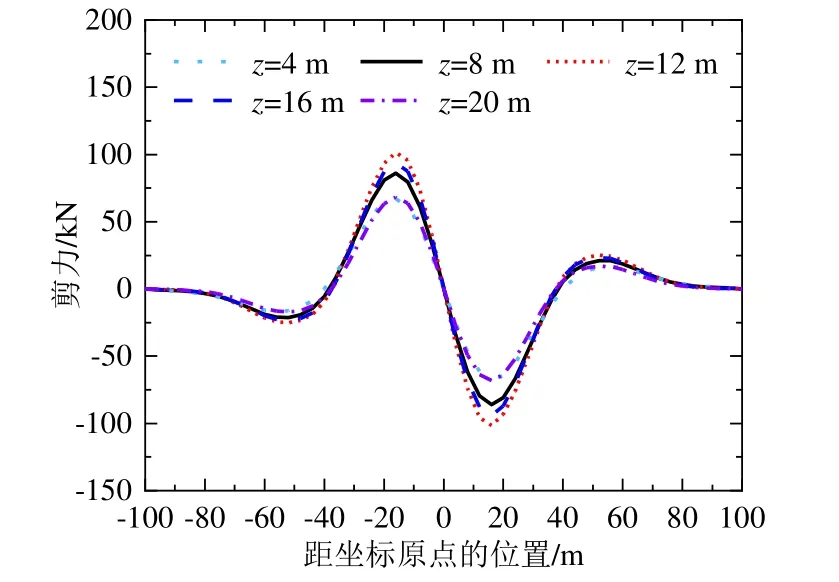
图10 不同隧道埋深下隧道剪力曲线Fig.10 Shearing force of the tunnel with different burial depths

6.3 围护墙最大变形的影响

由图11～13可见，随着围护墙最大变形的增大，隧道水平位移、弯矩及剪力也随之增大，且变形及内力的最大值与围护墙最大变形呈线性相关。当围护墙最大变形为20 mm时，隧道最大水平位移为6.0 mm，最大弯矩为0.9 MN·m，最大剪力为58 kN；当围护墙最大变形为50 mm时，隧道最大水平位移为15.0 mm，最大弯矩为2.3 MN·m，最大剪力为145 kN。因此，减小围护墙最大变形可有效降低基坑开挖的影响，控制邻近隧道的水平位移、弯矩及剪力。

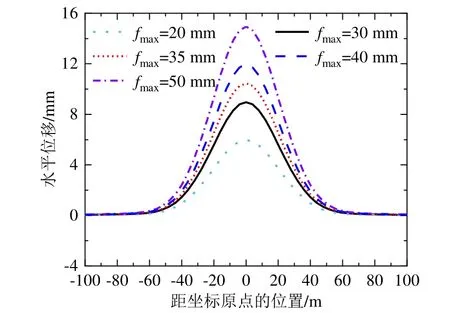
图11 不同围护墙最大变形下隧道水平位移曲线Fig.11 Lateral deformation of the tunnel with different maximum deformations of the retaining wall

图12 不同围护墙最大变形下隧道弯矩曲线Fig.12 Bending moment of the tunnel with different maximum deformations of the retaining wall

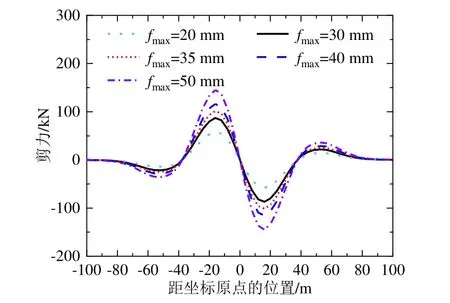
图13 不同围护墙最大变形下隧道剪力曲线Fig.13 Shearing force of the tunnel with different maximum deformations of the retaining wall

7 结 论

（1）基于围护墙变形空间曲面表达式，采用影像源法，得到了考虑基坑开挖空间效应的坑外土体附加变形计算方法。

（2）将隧道视为置于Winkler地基上的Timoshenko梁，基于两阶段分析法，将土体卸荷作用于隧道上，得到了邻近隧道附加变形的理论计算方法。

（3）通过与现场实测数据的对比，证明本文方法在隧道变形趋势及最大值预测上均有较好的可靠性及适用性。

（4）随着隧道与基坑边距离的增加，隧道水平位移、弯矩及剪力受基坑开挖的影响逐渐减小。

（5）隧道变形受隧道埋深的影响较大，应尽可能控制围护墙最大变形所在位置远离隧道埋深。

（6）隧道水平位移、弯矩及剪力最大值与围护墙最大变形呈线性相关，控制围护墙最大变形可以有效降低基坑开挖的影响，减小隧道的水平位移、弯矩及剪力。