复合地基沉降量计算的平均切线模量法
马 健
(北京环安工程检测有限责任公司,北京 100020)
0 引 言
近年来随着地基处理技术的发展,CFG桩复合地基在工程应用中取得了较大的进展,CFG桩通过褥垫层与基础联接,无论桩落在一般土层还是坚硬土层上,均可保证桩间土始终参与工作,桩、土共同承担荷载,减少了基础底面的应力集中。CFG桩复合地基对场地较好的高层建筑是适用的,它在满足设计要求的同时,方便了施工、降低了造价、节约了资金和时间,是一种比较理想的地基处理形式。工程实践表明,CFG桩复合地基对减小地基上建筑物的沉降和不均匀沉降有着明显的效果。不同的建(构)筑物对沉降变形有着不同的要求,在满足地基承载力要求的前提下,只要将CFG桩复合地基的沉降控制在允许变形的范围内,就能达到经济效益的最优和各种设计参数的合理组合。
目前CFG桩复合地基工程中确定地基承载力最可靠的方法是通过原位载荷试验[1]确定地基承载力的极限值,再除以两倍的安全系数得到满足地基承载力要求的地基承载力特征值,同时根据变形控制要求确定对应的地基承载力特征值,取两者较小值,就是最终确定的地基承载力特征值。由于地基承载力往往有足够的安全储备,其承载力安全性一般问题不大,但地基沉降变形难以准确计算。因此CFG桩复合地基的设计以控制变形为主要目标,地基的沉降计算应是目前需迫切解决的问题。
目前地基的沉降计算常用的方法是采用基于半无限线弹性体一维压缩变形假定条件下的分层总和法,其最大的难点在于计算参数的取用,即侧限压缩模量或变形模量的确定。国家标准《建筑地基基础设计规范》(GB 50007—2011)[2]采用的是室内试验确定的侧限压缩模量来计算地基的压缩变形,计算沉降与实际基础沉降的沉降差异则通过经验系数进行修正,国标《建筑地基基础设计规范》(GB 50007—2011)[2]经验系数为0.2~1.4,行标《建筑地基处理技术规范》(JGJ 79—2012)[3]经验系数为0.2~1.0。本文提出的平均切线模量法源于原状土切线模量法[4],该方法在原位载荷试验p-s曲线符合双曲线的基本假定条件下,采用切线模量法反算地基土层的切线模量E和抗剪强度指标黏聚力c,得到地基土层的变形和强度指标参数后,再用切线模量法计算实际基础的p-s曲线,进而确定实际基础的地基沉降量。由于该方法的切线变形模量源于原位载荷试验p-s曲线,因而能更好地反映地基的变形特征。本文通过在计算过程中对平均切线变形模量法进行优化改进,使得该方法进行地基沉降计算更加简便可行。
1 沉降量计算方法的讨论
1.1 规范法
国标《建筑地基基础设计规范》(GB 50007—2011)[2]采用室内试验确定的侧限压缩模量利用半无限线弹性体一维压缩变形理论分层总和法计算地基沉降量,再通过沉降经验系数对结果进行修正,以得到最终沉降量。该方法在工程中被普遍使用并积累了大量经验,但该方法仍具有一定的局限性。
(1)侧限压缩模量准确确定的局限性
目前一般的地基沉降计算主要依靠室内试验e-p曲线确定土试样的侧限压缩模量,但室内试验的参数一方面受取样扰动的影响,与实际原状土有较大的差异;另一方面地基土的压缩变形不仅与地基土的物理力学性质、变形指标有关,还与压缩试验承载板的尺寸有关。由于地基土压缩变形的尺寸效应,使得室内试验土试样的压缩模量远小于原位载荷试验反算的压缩模量。基于以上原因使得侧限压缩模量难以准确确定,只能采用经验系数对沉降量最终计算结果进行修正。
(2)沉降计算理论模型的局限性
现行规范在地基基础设计过程中地基承载力与沉降计算是分离的,地基承载力采用极限平衡理论通过抗剪强度指标黏聚力c和内摩擦角φ进行计算,沉降量计算采用线弹性理论通过压缩模量或变形模量进行计算,但地基其实是一个整体,由于缺乏有效的解决办法,把一个问题分解为两个近似问题来解决,这就导致了工程应用中地基承载力安全储备过高而地基沉降难以准确控制的问题。
1.2 原状土切线模量法
除规范法以外,如何取得原状土力学参数并把原状土的变形指标用于沉降计算还没有得到很好的解决。工程中直接可靠的方法是采用原位载荷试验来确定地基的承载力及原位变形模量,但实际上地基的承载力及地基沉降变形不仅与地基土的物理力学性质、强度参数、变形指标有关,还与基础的尺寸有关。原位载荷试验通常是进行小尺寸无埋深的试验,不可能用实际基础尺寸来进行试验,这就存在一个如何用小尺寸的压板载荷试验来确定实际大尺寸基础下地基的承载力及变形模量的问题,这个问题理论上没有得到很好的解决。
原状土切线模量法假定原位载荷试验p-s曲线符合一双曲线方程[4-5],即:
通过原位载荷试验p-s曲线的拟合可以得到a和b;再通过计算推导得到计算公式[6],即:
式中:D为试验的压板直径;μ为土的泊松比;ω为刚性承载板的形状系数;E0为原状土的初始切线模量;Et为承压板下土体对应某一荷载p处增加一增量荷载时的土体等效平均切线变形模量;pu为根据《工程地质手册》[7]中地基极限承载力公式计算确定的地基极限承载力。
杨光华等[8]认为p/pu是压板底面处所受压力p与极限荷载pu的比值,反映了土体应力水平对土体切线模量的影响。式(4)表明,土的切线模量取决于p/pu比值,而不仅仅取决于p值,因此随着埋深越大,对应该点的pu越大,则由式(4)可知对应的Et越大,可以由此计算实际基础尺寸下不同深度处地基土的变形模量,进而采用分层总和法计算地基最终沉降量。因此,考虑应力水平影响确定切线模量Et更符合实际。
笔者认为Et的含义是代表承压板下土体对应某一荷载p处增加一增量荷载时的基底压力影响深度范围内总土体的等效平均切线变形模量,而非代表选取某一计算厚度土层的切线变形模量。例如假设地基计算深度为10 m,分10层计算,利用上述方法计算第一层的切线变形模量时采用1 m深度应力扩散后对应的附加应力p1和1 m埋深处对应地基极限承载力pu1,认为计算得到了第一层土层的切线变形模量Et1,而该Et1实际代表的应该是1 m以下9 m范围内总土体的等效平均切线变形模量。并且初始切线变形模量E0也是原位载荷试验p-s曲线上荷载p无限接近0时,增加一增量荷载的基底压力影响深度范围内总土体的等效平均切线变形模量,所以Et的意义也在于此。上述算法实际上对承载板或实际基础下地基土的变形模量进行了重复叠加使用,沉降计算结果应是偏大的。
实际上,地基深部土体的变形模量理应是埋深越大变形模量越大的[9],这是毋庸置疑的,只是上述公式计算的值所代表的含义并不是某一深度土体单元的变形指标,而是计算深度范围内土体总体的一种等效的指标,其内里已包含了变形模量随深度的变化。
因此本文中反算的Et1代表的是承压板下土体对应某一荷载p处增加一增量荷载时的基底压力影响深度范围内总土体的等效平均切线变形模量,用这种取值来进行实际基础的沉降变形计算,即平均切线变形模量法。
2 平均切线模量法
某CFG桩复合地基工程进行原位载荷试验,地基承载力特征值为450 kPa,最大加载值为900 kPa,承载板尺寸为1.5 m×1.5 m,加载分级为10级,每级荷载90 kPa,原位载荷试验的试验曲线及验证曲线见图1。
根据原位载荷试验的p-s曲线计算确定E0、pu值,再由式(4)可反算得到不同荷载水平承载板下地基土总体的平均切线变形模量,以其代替传统分层总和法的压缩模量,采用分层总和法计算载荷试验下的p-s曲线,与实测的p-s曲线进行比较,从而检验本方法的可行性。具体过程如下:
如图2所示,可得a=0.004 146,b=0.000 803,土的泊松比μ按0.25考虑,正方形刚性承载板的形状系数ω=0.886,假定地基土内摩擦角φ=25°,则Nc=20.72,Nd=10.66,Nb=10.88,d=0 m,b=1.5 m,试验场地地下水位较浅,故γ0=γ=10 kN/m3。
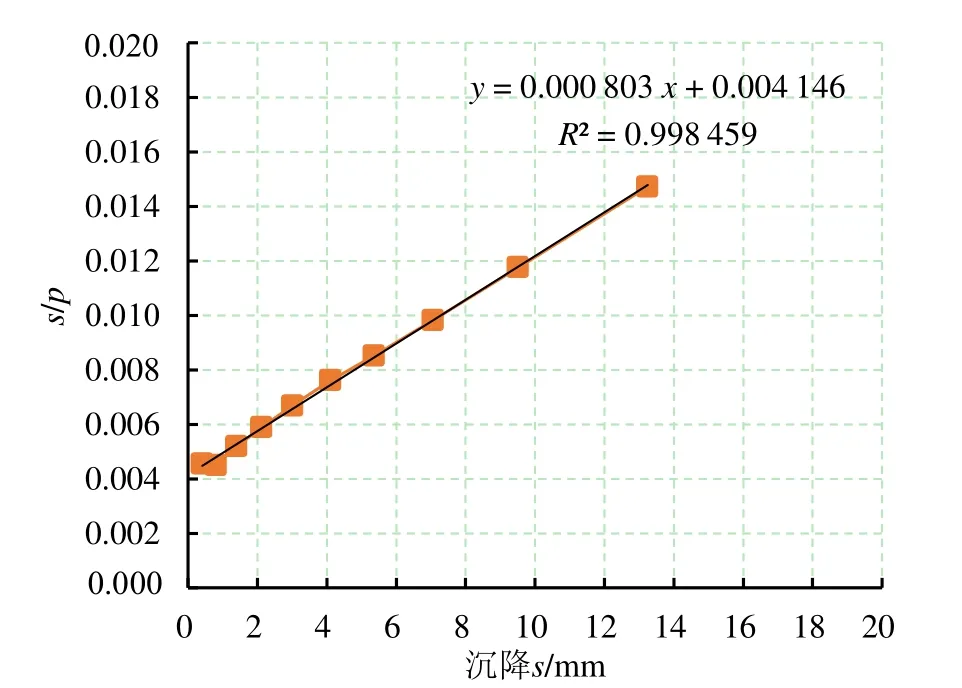
图2 原位载荷试验的拟合曲线Fig.2 Fitting curve of in-situ loading test
按式(2)~(3)可得E0=300.52 MPa,pu=1 245.33 kPa,按式(5)反算可得c=56.16 kPa,按式(4)依次求得不同荷载水平下的平均切线变形模量Et,计算过程中采用每一荷载段中值荷载所对应的切线变形模量代表该段荷载的平均切线变形模量,如图3所示,荷载越大,切线变形模量的变化率越小,因此荷载段中值对应的切线变形模量比荷载段两端荷载对应的切线变形模量的平均值更保守,即0~90 kPa荷载段计算沉降时采用45 kPa荷载水平对应的切线变形模量,即:
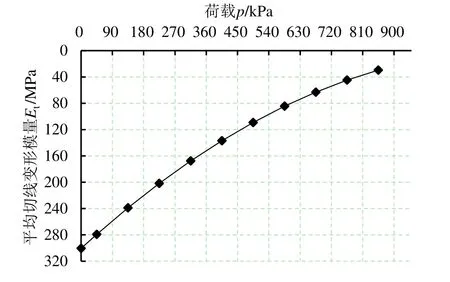
图3 原位载荷试验的切线模量曲线Fig.3 Tangent modulus of in-situ loading test
荷载增量段0~90 kPa采用p=45.00 kPa计算得:
荷载增量段90~180 kPa采用p=135.00 kPa计算得:
其他同理计算。
根据分层总和法[10],式(6)计算各荷载水平下增量荷载Δp=90 kPa时的分级沉降量,沉降计算深度取30 m,详细计算结果如表1所示。
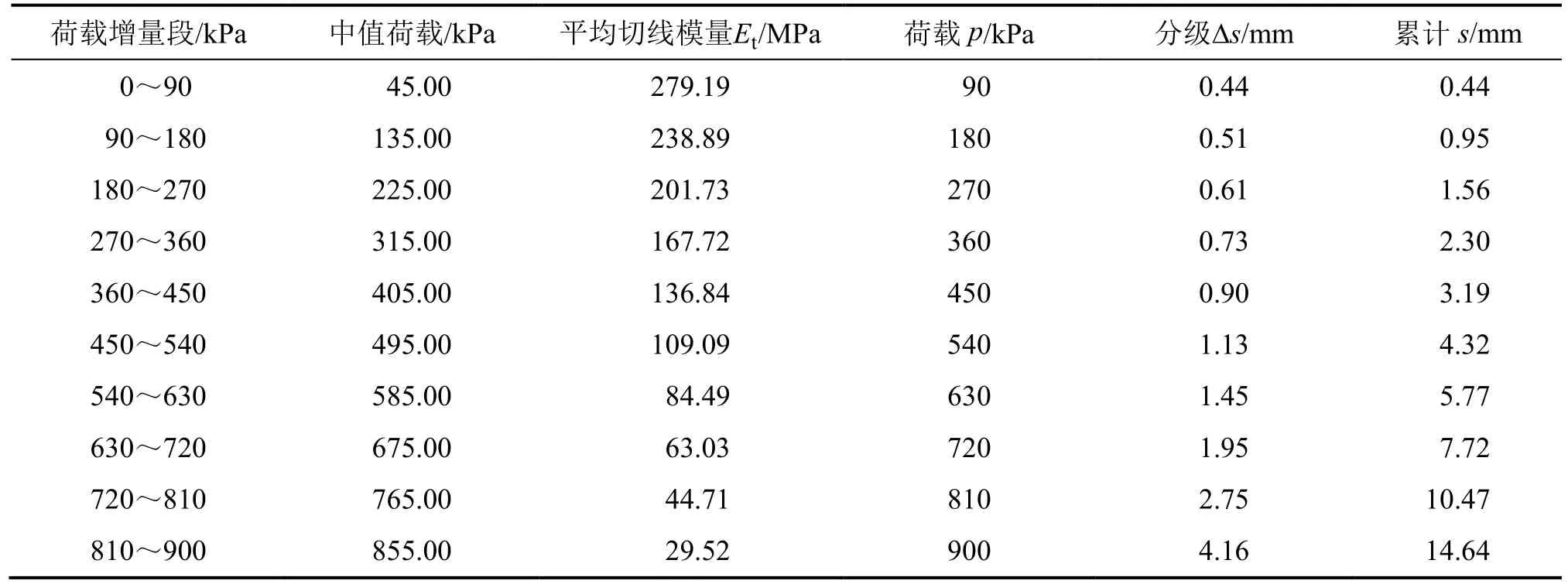
表1 沉降量计算表Table 1 Settlement calculation
通过以上计算得到验证曲线,如图1所示,验证曲线与原位载荷试验曲线基本一致,说明通过平均切线模量法计算得到荷载曲线是可行的;计算值略大于实测值说明平均切线模量法是偏于安全的。
3 案例应用
现在利用上述工程的原位载荷试验p-s曲线和平均切线模量法来计算实际基础尺寸下的载荷p-s曲线。该工程为1栋塔楼,地上25层,地下2层,采用箱型基础,基础埋深5.85 m,地下水位于地表以下1.4 m,基础尺寸为30 m×30 m,基底压力为450 kPa,沉降量允许值为60 mm。CFG桩复合地基采用正方形布桩,桩间距1.5 m×1.5 m,桩长18 m。原位载荷试验p-s曲线即上述曲线(图1),地基土层物理力学指标统计表如表2所示。
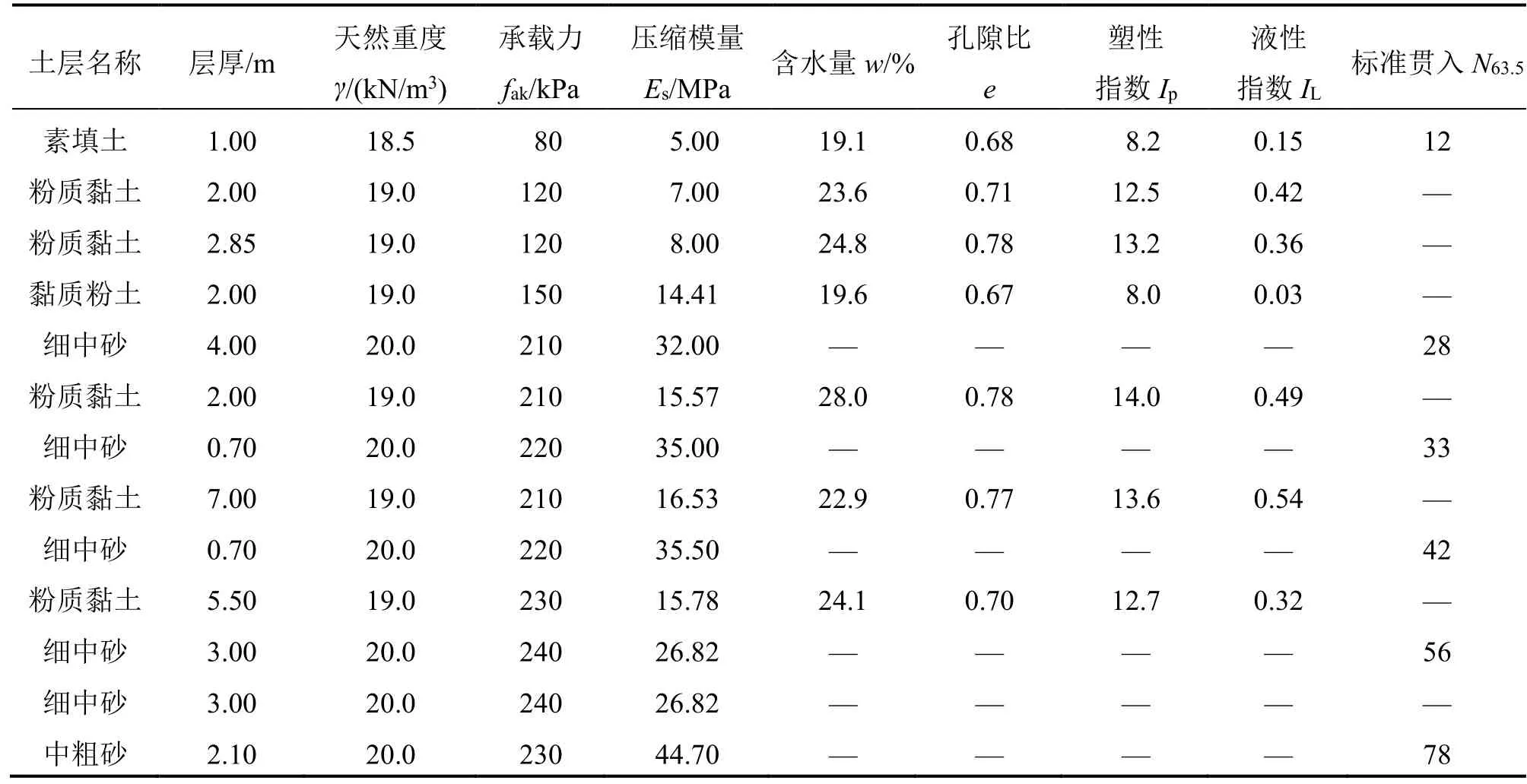
表2 地基土层物理力学指标统计表Table 2 Physical and mechanical indexes of foundation soil layer
由上述原位载荷试验p-s曲线反算得c=56.16 kPa,地基土内摩擦角φ=25°,则Nc=20.72,Nd=10.66,Nb=10.88,d=5.85 m,b=30 m,地下水位较浅,故γ0=γ=10 kN/m3。按式(5)计算得pu=3 419.34 kPa,初始切线模量仍为E0=300.52 MPa。
按上述过程计算得到实际基础沉降量计算如表3所示及实际基础的计算荷载曲线如图4所示,沉降计算深度取30 m,满足计算要求。
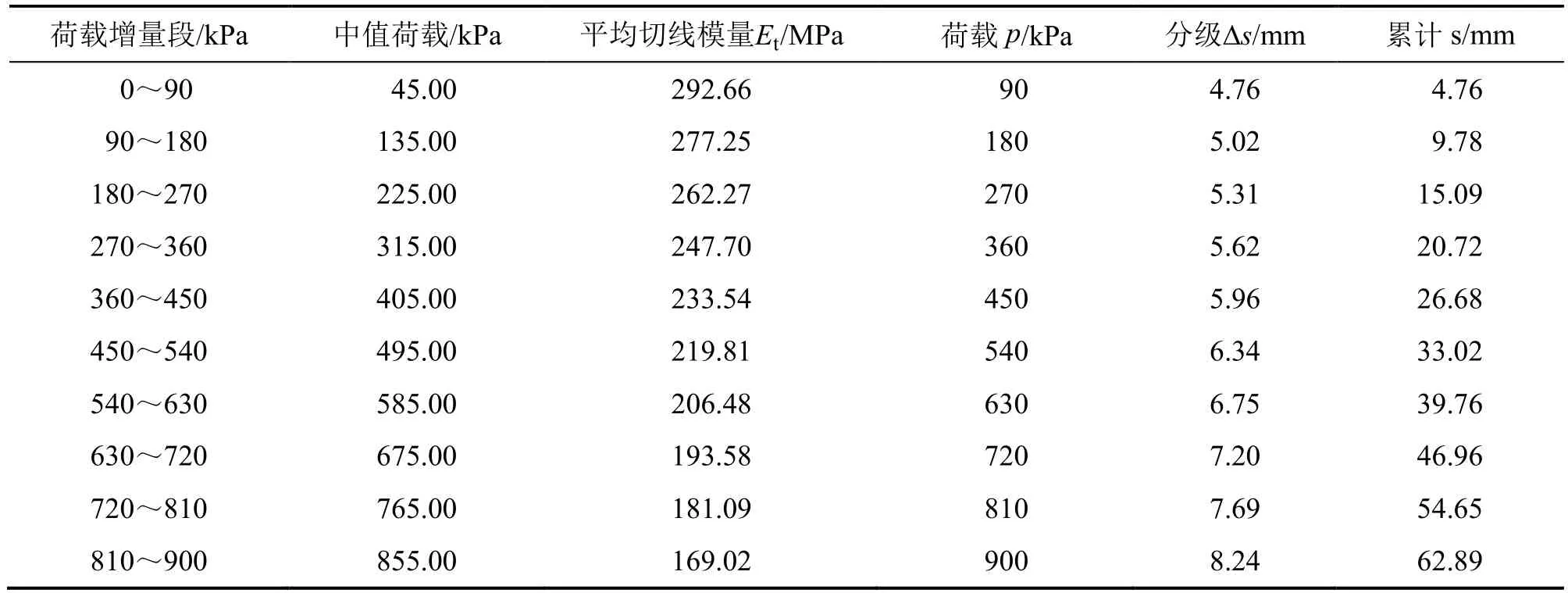
表3 实际基础沉降量计算表Table 3 Calculation of foundation settlement
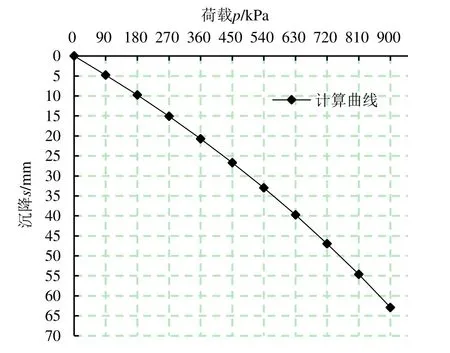
图4 实际基础的计算载荷曲线Fig.4 Calculated curve of p-s results
规范法计算实际基础沉降量见表4,经计算复合地基承载力特征值fspk为400 kPa,修正后复合地基承载力特征值fspa为464.9 kPa,满足地基承载力设计要求,沉降计算深度取30 m,满足计算要求。
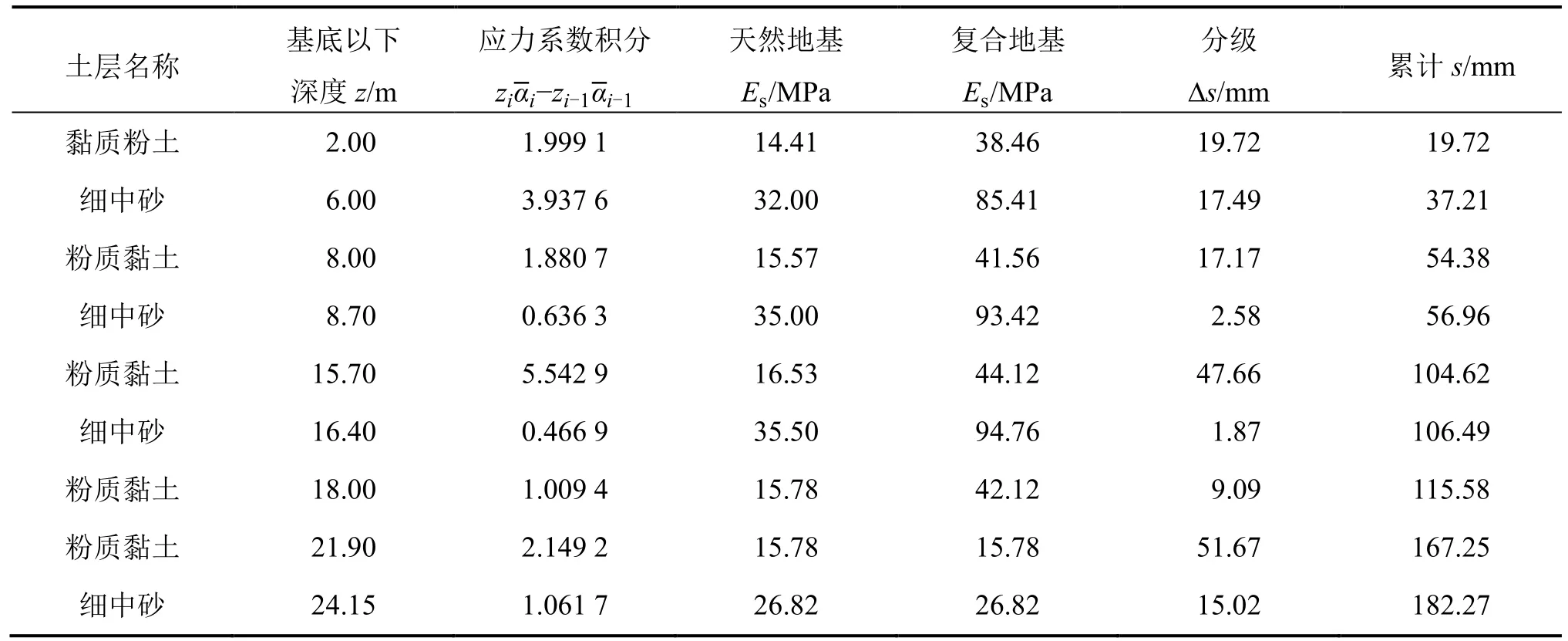
表4 实际基础沉降量计算表(规范法)Table 4 Calculation of foundation settlement (specification method)
经计算压缩模量的当量值为38.889 MPa,沉降计算经验系数取0.200,总沉降量为36.45 mm。
基底压力按450 kPa考虑时,平均切线模量法计算沉降结果与规范法计算沉降结果、竣工时沉降监测结果对比情况见表5。

表5 计算沉降与实测沉降结果对比Table 5 Comparison between calculated settlement and measured settlement mm
结果表明,用平均切线模量法计算的沉降量与实际沉降量较接近,而规范法计算结果偏大,虽然都符合地基允许沉降量60 mm的要求,但平均切线模量法较符合实际。
4 结 论
(1)现行规范中地基沉降量计算方法主要依靠室内试验确定的压缩模量,但室内试验的参数与实际原状土有较大的差异,且地基沉降量的计算不仅与地基土的物理力学性质、强度参数、变形指标有关,还与基础的尺寸有关,因此本文采用原位载荷试验曲线反算得到地基土变形参数,进而求得实际基础尺寸的地基沉降量,具有较好的科学合理性。
(2)平均切线模量法在变形模量的选取上采用某一荷载段中值对应的切线模量代表增量荷载下地基土沉降计算深度范围内土体总体的等效平均切线变形模量,使计算过程简化,易于理解,并且计算结果与实测结果具有较好的一致性。
(3)文中根据原位载荷试验反算实际基础地基沉降过程中有着诸多假定前提条件,合理确定计算参数是地基沉降计算的关键。在CFG桩复合地基工程中,由于桩土共同承担荷载、共同发挥作用,其更接近于一个均质的线弹性体地基,因而在变形参数上具有较好的均一性,采用平均切线变形模量参数进行计算更具代表性。在工程实践中需要进一步积累经验,不断完善,以更好地用于解决地基沉降计算问题。

