一道解析几何综合题的探究

刘 海

⦿ 江苏省曲塘高级中学

平面解析几何中的最值(或取值范围)问题,往往以“压轴题”的形式出现在高考选择题、填空题或解答题中的对应位置,成为高考命题乃至自主招生、竞赛中的“常客”之一,更是各类模拟考试中常考的基本题型之一.此类问题,除了可以很好地考查平面解析几何的基本知识,还可以巧妙融合平面几何、函数与方程、三角函数、不等式、函数与导数等其他相关知识,契合“在知识交汇点处命题”的命题理念,同时又能很好考查学生基本的数学思想方法和核心素养等,创新新颖,花样翻新,难度较高,但其基本解题思路与技巧方法仍然有章可循,有法可依.

1 问题呈现

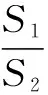
此题以抛物线、圆为综合问题载体,结合直线与抛线物、直线与圆的位置关系,以及坐标原点与交点所构成的三角形的面积,通过两个不同三角形的面积的比值创设,进而确定相应的最值问题.

本题解题的关键是构建两个不同三角形面积的表达式,合理引入参数是根本所在.可以通过设线法、设点法或参数方程法等多思维视角切入,利用三角形面积公式的不同形式来确定对应的面积表达式,为进一步确定面积比值的最值提供解题依据与基础.

2 问题破解

方法1：设线法.

图1

解析：由题意可知,直线AB的斜率不为0,故设直线AB的方程为x=my+4.

如图1所示,设A(x1,y1),B(x2,y2),P(x3,y3),Q(x4,y4).

将直线AB的方程代入圆E的方程,消去参数x并整理,可得(m2+1)y2-12=0.

利用韦达定理,可得

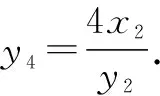
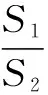
解后反思：设线法是处理直线与圆锥曲线位置关系问题中比较常用的一种“通性通法”,巧设直线方程,与圆锥曲线的方程联立,利用函数与方程思想,通过韦达定理构建相应交点的坐标关系式,为进一步分析与探究提供条件.设线法往往要结合直线的斜率是否存在、是否为零等信息加以创新设置,其目的是回避分类讨论,优化解题过程.

方法2：设点法.

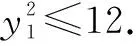
以AB为直径的圆E的方程为

(x-x1)(x-x2)+(y-y1)(y-y2)=0.

整理,可得x2-(x1+x2)x+x1x2+y2-(y1+y2)y+y1y2=0=x2-8x+y2+4.

所以x1+x2=8,y1+y2=0,x1x2+y1y2=4.

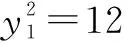
解后反思：设点法也是处理直线与圆锥曲线位置关系问题中比较常用的一种“通性通法”,借助点的坐标的设置,可以建立直线方程、构建坐标参数所满足的关系式等,结合题设条件可以合理“串联”起不同坐标之间的关系,以方便问题的进一步分析与解决.设点法往往抓住点所在的直线、圆锥曲线等加以合理设置,尽量减少参数的个数,以方便后继的数学运算与综合解题.

方法3：参数方程法.

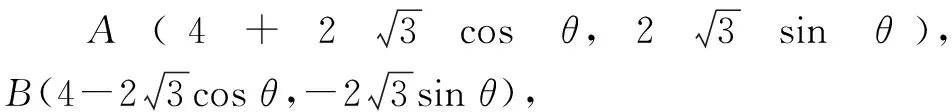
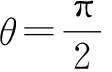
解后反思：参数方程法是处理直线与圆锥曲线位置关系问题中比较常用的一种“巧技妙法”,借助直线、圆、圆锥曲线等参数方程的设法,对应直线或曲线上相应点的坐标,通过参数的变化进一步分析与求解实际问题.参数方程法的应用过程中,要注意点参、线参、角参等取值范围的限制,要合理挖掘题设条件,正确加以确定,这对后继的数学运算与解题起到至关重要的作用.

3 教学启示

3.1 归纳总结方法,养成解题习惯

求解平面解析几何中的最值(或取值范围)问题时,要抓住直线与圆锥曲线的位置关系等场景,巧妙选取合理的参数,如点参、线参、角参等,同时结合题设条件或隐含条件等确定对应参数的取值范围.

在设参的基础上,借助直线与圆锥曲线的位置关系等切入,巧妙建立关于相应参数的目标函数,进而利用圆锥曲线自身的几何性质,或借助二次函数、基本不等式、函数与导数等来分析与求解对应的最值(或取值范围)问题.

3.2 “一题多解”思维,深入研究拓展

解平面解析几何的最值(或取值范围)问题时,由于参数选择的形式多样,根据题设合理选择点参、线参、角参等,这就为解决此类问题提供了更加丰富多彩的思维视角,是实现多种方法解题的根本,可以很好实现“一题多解”的巧妙应用,同时对不同的技巧方法加以对比、分析,从中合理优化,提升能力.

基于此类问题的“一题多解”,可合理对问题条件、问题结论,以及问题的求解方法、求解过程等加以深入研究与分析,从而合理拓展与应用,达到“一题多思”“一题多变”“一题多得”等方面的良好效果,对于全面提升数学解题能力以及培养数学核心素养都有益处.