思维可见的小学数学探究性作业设计与实施

宋霞娟　王东平

摘 要 促进学生思维发展是数学学科的核心使命，也是落实数学核心素养的关键所在。作业作为教学的重要环节，既是对课堂知识和内容进行巩固和拓展的重要手段，也是培养学生数学思维能力的重要载体。以小学数学探究性作业为载体，让学生在“画”数学、“说”数学、“做”数学的过程中，将隐藏的思路显性化、零散的知识系统化、抽象的模型具体化，可以实现学生思维可见，促进学生思维发展。

关  键  词 小学数学；探究性作业；“画”数学；“说”数学；“做”数学

引用格式 宋霞娟，王东平.思维可见的小学数学探究性作业设计与实施[J].教学与管理，2024（05）：64-67.

思维可见，就是让思维看得见。由于思维本身是无法可视的，所以需要借助一系列技术和活动把学生的思维方法和思考路径一一呈现出来，使其清晰可见[1]。研究表明，可见的“思维”更有利于理解和记忆，可以有效提高信息加工及信息传递的效能。作业是促进学生学习思维外显，促进学习情境和学习规则落实的、可见的重要载体之一。“双减”政策明确提出，要减轻学生的作业负担，大力倡导探究性、实践性作业[2]。在这一背景下，我们以学生学科核心素养培养为出发点，通过设计大量探究性作业，代替原有重复性、机械性作业，让学生的数学思维在自主探究过程中得以外显化，并让学生爱上思考、学会思考，提升思维品质和学习力。

一、“画”数学：通过图形看见思维

在关注学科核心素养的当下，“用数学的语言表达现实世界”已经成为共识，“画”数学便是学生用自己的语言表达数学的方法之一。“画”数学是指学生在学习数学的过程中，运用感知觉和表象，将抽象的数学概念、数学规律、数量关系等通过形象的图示、表格等看得见的形式表示出来。让学生动手画，画出数学，就是耐心地让学习真实发生，让思维流淌[3]。

1.“画”流程，让解题思路看得见

“画”流程是指学生在解决数学问题的过程中，把解决问题的步骤画出来。“画”的过程，能将疑难问题的文字翻译成图，能够立竿见影地厘清思路，帮助学生找到解题策略，更为重要的是，能让隐藏在学生头脑中的数学算法、数学思想和解决数学问题的策略外显化，有利于学生审视自己的解题思路、发现错误，同时有利于教师发现学生思维的薄弱或错误之处。例如，在学习了“分数乘分数”一课后，设计探究性作业（如图1）：（1）自行设计一道分数乘分数的题目，两个分数最好是最简分数；（2）探究如何列竖式计算分数乘分数（提示：可以先将分数乘分数转化为整数乘整数，再由整数乘整数的积得到分数乘分数的积）。

“画”流程是学生个性化解决问题的方式之一。解决问题的算式也许是相同的，但是算式背后的思考却各不相同，也就是每位学生对问题的理解方式各不相同。“画”可以让每一位学生的思考变得与众不同，让每一位学生的思考跃然纸上、呈现画中，让思维可见。

2.“画”模型，让解题要素看得见

“画”模型的过程就是从抽象的文字到直观的图形的再创造、再演示的过程，如画线段图、几何草图等。一些数学问题的数量关系比较复杂，学生难以厘清，借助“画”模型，可以把复杂的数学问题变得简明，同时也可以让解题要素和学生思维看得见[4]。例如，在学习了“和倍问题”后，设计了利用线段图解决问题的探究性作业（如图2）。

画图，一目了然。从学生反馈的结果来看，大部分学生能把抽象的数量关系形象地展现出来，但也存在不少问题：有的学生在解题过程中忽略了题目中的条件，有的学生在画线段图时对“？”到底标在什么地方模糊不清。这时，教师可以有针对性地进行辅导和纠正，助推学生思维发展。

3.“画”导图，让知识生发看得见

思维导图是一种图形思维工具，通过图文并重的技巧，使主题关键词与图像、颜色等建立记忆链接，可以帮助我们厘清思绪，重塑更加有序的知识体系[5]。

将思维导图引入数学探究性作业设计中，可以促进学生建构知识网络，提升注意力和记忆力，同时也能让学生的思维清晰可见。例如，在学习了“倍数与因素”单元内容后，教师布置用思维导图进行单元知识探究的作业，要求：8K纸，层次清晰，知识点清楚，字迹工整，画面美观。学生作业如图3。

画思维导图的探究性作业，既能梳理因数与倍数的相关知识，又能让学生的学习思维清晰可见；既启发学生的创造性，又增强他们的动手能力。

二、“说”数学：通过语言表现思维

学之道，在于辨，在于说，在于悟。语言是思维的外壳，“说”数学，就是引导学生用数学语言来叙述自己的解题思路、思考体会，把自己的想法、思考过程讲出来。这一过程，能让学生的思维更加清晰、明了，同时也能让学生经历探理、说理、辩理、悟理的过程。

1.数学小讲堂，让数学思维得以展现

会做题是数学学得好的一个方面，而会讲题则代表学生对数学题目蕴含的道理有了更深入和透彻的理解，是解决问题的最高境界。开口讲数学，有利于学生思维外显，促进师生、生生互相学习，共同提高；有利于培养学生的探究精神，促使他们多角度、深层次挖掘题目的内涵与外延；有利于提高学生的学习兴趣和信心，增强学生学习内驱力；有利于提高学生的思维层次，实现从“会做”到“会讲”，再到“讲会”。

例如，在学习数正方体个数时，学生的易错点主要是：根据从某一方向观察到的平面图形，无法判断几何体的摆法，更无法确定组成这个几何体的小正方体的个数。为了帮助学生更好地掌握数正方体个数的问题，教師可以设计“数正方体”的数学小讲堂探究性作业：图4由几个小正方体拼搭而成，你会怎么数？

我们可以一层一层数或一排一排数，也可以先数看得见的块数，再数看不见的块数。不管哪一种方法，我们在数的时候都要按照一定的顺序，做到不重复、不遗漏。在课堂展示过程中，学生重点介绍了后一种方法，看的见的有2+2+1=5（个），看不见的有2个，所以一共有5+2=7（个）小正方体。让学生通过画的方式表达自己对概念的理解，使隐性的知识显性化、可视化；用讲的方式把自己的思维过程有序地表达出来，真正内化为自己的认知结构。

2.角色扮演，发现思维漏洞

数学是数学逻辑的构建，是数学思维的碰撞，是数学规律的探索。设计“小医生”角色扮演活动，可以让学生对自己的错题进行诊断，通过分析病因，发现错题原因，并提出解决策略，不仅可以让学生的思维可见，更为重要地是通过医生诊断活动的开展，有利于发现学生思维漏洞，不断完善和修正学生思维，进而实现高阶思维的发展。

在“数学门诊”部设有“专家门诊”和“普通门诊”，看病对象是“病题库”中的“病题”，这些题目主要是学生日常作业、考试中的错题。“专家门诊”重点诊治病题库中有难度的错题，而“普通门诊”主要诊治一些容易解决的错题。“小医生”为班级的每一位学生服务，学生自愿选择去“专家门诊”或“普通门诊”为各种病题诊脉、开方。例如，在学习“乘法分配律”后，首先由每位学生为自己做一个全身体验，把自己在运用乘法分配律时的错题找出来，形成病题库，然后由“小医生”坐诊，对各种病题“诊脉”，并开出“药方”，实现“话”到病除。以下是一位“小医生”的诊治过程：67×101-67=（67-67）×101=0。我们不应该把67提到前面来，这样是错误的。先看算式，算式非常类似于乘法分配律，那我们就把乘法分配律的公式写出来：a×b-a×c=a×（b-c）；我们再看题目，题目中有a，有b，但是没有c，那能不能造出c呢？仔细看67乘以多少还是等于67呢？显然是1，所以我们的式子可以改写成67×101-67×1，这样我们就能运用乘法分配律得到67×101-67×1=67×（101-1）=6700。

听明白不一定真的明白，说明白才是真的明白。“小医生”坐诊中不仅需要学生对“病题”的病因进行描述，还需要学生提出有效的“抗病”策略，让学生的思维过程清晰可见，同时也让学生真实地参与到数学学习的过程中，真正地理解知识、掌握知识。

三、“做”数学：通过探究发展思维

陶行知先生强调“教学做合一”，在这一思想指导下，设计数学探究性作业，可以让学生在“做”数学的过程中通过观察、操作、调查等方式，提升探究应用、问题解决等能力，促进学生思维能力的发展。

1.合作探究作业：促进集体思维碰撞

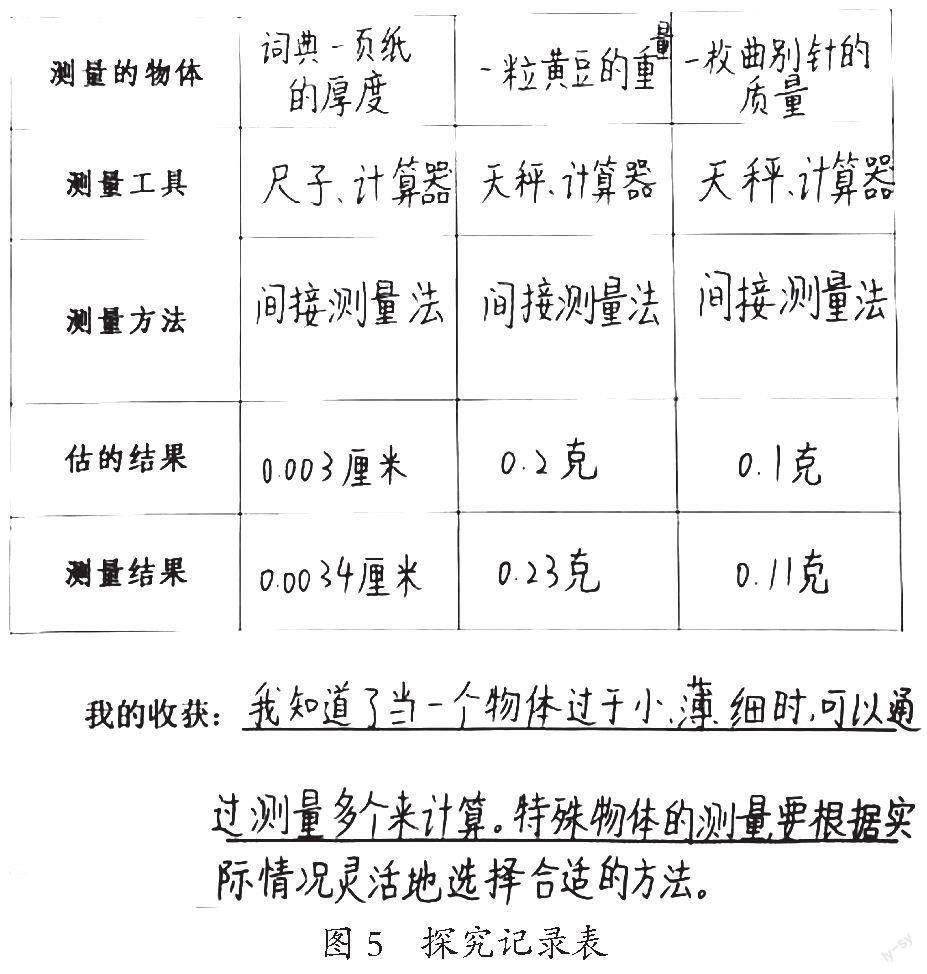
“双减”政策下，教师在设计作业时要突出合作探究，以实际问题为载体，设计让学生自主参与探究的作业，引导学生进入研究角色，学会与他人合作，实现个人思维与他人思维的相互碰撞。例如，我们身边，有一些特殊的物体，它们的长度、质量、面积是很难直接测量出来的，你们想怎样测量呢？以小组合作的形式设计测量方案，交流测量方法，通过比一比、称一称、量一量、算一算等不同方法巧妙地测量出不同物体的长度、质量和面积等，最后把实验过程和结果呈现在图表里（如图5）。

在探究性作业的完成过程中，学生通过集体智慧的相互碰撞和动手实践，灵活地选择合理、快捷的测量方法测量并计算，最后用图表的形式将小组整个思维过程清晰地呈现出来，有效促进学生思维的发展。

2.跨学科作业：综合运用学科思维

《义务教育课程方案（2022年版）》修订原则中提出：“要加强课程内容与学生经验、社会生活的联系，强化学科内知识整合，统筹与设计综合课程和跨学科主题学习。”跨学科探究性作业的设计，可以打通学科之间的壁垒、联通学科之间的脉络，提升学生综合运用学科思维的能力。

例如，在学习“用方向和距离描述位置”一课时，要让学生学会利用方向和距离这两个参数，确定平面上一个点的位置，会描述简单的路线图。由此，在课后综合美术、地理等学科知识，设计跨学科探究性任务：

请你绘制一份从学校回家的路线示意图，注明方向和途中的主要参照物，并将路线图描述出来（可以利用互联网，查出你家附近的地图，以便更准确地描述）。

要求：（1）在路线图上标注清楚角度、距离、地点、名称，要求至少五个地点；（2）用文字准确描述往返路线；（3）可以选择购物路线、锻炼路线、旅游路线，可以是平时行走过的路线，也可是虚拟路线，适当装饰美化。

探究性任务指向路线图的绘制与描述这一核心知识点。绘制路线图，用方向和位置确定位置；描述路线图，侧重于用数学语言，精确地描述位置与路线。从学生作品中暴露出以下几点问题：一是图上方向与实际方向脱离；二是实际路线转换不准，脱离实际；三是个别同学描述路径时，语言还停留在口语表达，未能使用数学语言精确表达（如图6）。由此可见，学生对如何运用方向和距离这两个参数来准确描述具体位置还不够熟练，有待进一步巩固和强化。

在探究性作業中，学生用数学的眼光观察现实世界，用智慧的头脑发现问题，用学科思维积极思考和解决问题，不仅激发了学生学习的热情，发展了学生的空间观念，展示了学生的创造智慧，锻炼了学生将数学知识应用于生活的能力，而且在绘制线路图和用语言表述的过程中，让学生的思维过程清晰可见。

总而言之，指向思维发展的数学探究性作业，是基于学生生活实践、教材内容和知识点等多个角度设计的操作思考性作业，可以引发学生的思考与探究，其最终目的是通过思维可见促进学生的思维发展。教师应在学生思维工具和逻辑发展上重点突破，通过“画”数学、“说”数学、“做”数学的深化研究，发展学生数学眼光、深化学生数学思考、强化学生数学语言，加强数学表征与实践，助力学生从思维可见向思维发展转变，从而提高学生的数学核心素养。

参考文献

[1] 邵虹.审辩课堂：看见思维、赋能学习[J].小学数学教师，2023（09）：8-13+2.

[2] 黄建.在慎思、明辨中感悟整数乘法运算的一致性——以“三位数乘两位数”为例[J].小学数学教师，2023（09）：18-21.

[3] 陈雁斌.思维可视化技术在小学数学教学中的应用策略分析[J].数学学习与研究，2023（19）：74-76.

[4] 王芳珍，高思远.数学课堂，让“深度学习”真实发生[J].数学学习与研究，2023（19）：104-106.

[5] 李晓梅.小学数学教学中独立思考能力的培养[J].数学学习与研究，2023（19）：71-73.