产水气井冲缝套动态冲蚀机理研究

邓福成 李艺谋 龚 宁 韩耀图 许朝辉 邓君宇 陈 竹

(1.长江大学机械工程学院 2.中海石油(中国)有限公司天津分公司 3.中国石油集团工程技术研究院有限公司 4.中国石油集团工程技术研究有限公司 5.广东省海洋协会)

0 引 言

我国西部某气田属于深层异常高压凝析气藏，某井开采一段时间后开始产水，数月后，陆续出现油嘴堵塞、油嘴冲蚀和套管堵塞等异常情况。现场多次更换管柱，产气量仍然下降，且再次出砂时间的间隔较短、多次异常关井，说明防砂筛管已经失效，服役寿命远短于预期。研究冲缝筛管在腐蚀环境下的冲蚀机理，对产水气井的防砂及冲缝筛管设计具有重要意义。

油管钢也用于制作筛管，其腐蚀试验具有一定参考价值。P110S油管在腐蚀环境中，以CO2腐蚀为主，高温和高含量的Cl-能加快腐蚀反应速率[1-3]。N80油管在腐蚀环境中，H2S分压是最敏感的因素之一，其次是温度、Cl-含量和CO2分压[4-5]。多种含铬油管(S13Cr、13Cr、15Cr、25Cr)在高温、高H2S分压的腐蚀环境下适用，但在腐蚀环境中长时间服役仍有氢致开裂的风险[6-9]。与H2S、CO2单独存在的环境相比，H2S/CO2共存的腐蚀环境对油管的危害更大，开发出经济性较好的耐腐蚀钢材和防腐措施(防腐涂层、缓蚀剂)是未来研究的热点领域[10-11]。学者们对防砂筛管的结构件也进行了腐蚀试验，试验结果表明，冲缝套腐蚀速率大于筛网腐蚀速率，但是筛网结构更细，所以寿命更短[12-13]。在腐蚀环境中，筛网会早于冲缝套失效，在冲缝套失效后，筛网质量损失速率会更大。

长期来看，腐蚀是筛管质量损失的主要原因，但是冲蚀造成的质量损失也不能忽视。陈珊珊等[14]对金属网布筛管局部三维模型进行仿真模拟，研究金属网布筛管的速度分布、切应力分布和冲蚀速率分布。邓福成等[15]建立了冲缝套单元模型，通过CFD技术探究了不同因素对冲蚀磨损的影响，发现冲蚀磨损发生在冲缝套底部边缘。这些研究仅静态模拟冲缝筛管的冲蚀，没有考虑腐蚀作用。为此，笔者通过腐蚀试验，测得S13Cr材料的腐蚀速率，建立含腐蚀缺陷的冲缝套流道模型，并考虑腐蚀造成的质量损失和变形，研究缺陷对冲缝管套冲蚀的影响，进行气-液-固三相流动态数值模拟。

1 腐蚀试验

1.1 试验条件

腐蚀试验依据GB/T 19291—2003和JB/T 7901—2001，腐蚀试验装置原理图和挂片结构示意图如图1所示。腐蚀试验主要考察含水体积分数变化对腐蚀的影响，将凝析油和水按不同体积分数配比制作腐蚀介质，然后注入气体模拟井下环境，试验条件如表1所示。采用失重法对试验结果进行处理，腐蚀速率为：

(1)

式中：Vc为腐蚀速率，mm/a；ρ为挂片密度，g/cm3；s为挂片表面积，cm2；t为腐蚀时间，d；m0为挂片腐蚀前的质量，g；mt为挂片腐蚀后的质量，g。

图1 试验装置及挂片示意图Fig.1 Schematic diagram of test device and coupon

1.2 试验结果

腐蚀试验结果如图2所示。由图2可知，含水体积分数从0增长到100%，腐蚀速率从0.011 5 mm/a增长到0.039 9 mm/a。试验结束后，去除腐蚀产物，挂片的腐蚀样貌如图3所示。由图3可知，挂片整体呈现均匀腐蚀特征。通过激光共聚焦测量腐蚀坑的深度，腐蚀坑的3D形貌如图4所示。

表1 腐蚀试验条件Table 1 Conditions for corrosion test

图3 挂片的腐蚀样貌Fig.3 Corrosion appearance of coupon

图4 腐蚀坑的3D形貌Fig.4 3D morphology of corrosion pit

2 模拟理论

2.1 冲蚀速率模型

国内外学者经过多年研究，建立了冲蚀模拟理论[16-20]。这些理论应用在CFD仿真中。产水气井出砂过程涉及气-液-固三相流动，数值模拟要计算连续相(气液)之间的相互作用，同时计算连续相(气液)和离散相(固)之间的相互作用。最后计算出颗粒对壁面造成的冲蚀速率，冲蚀速率为：

(2)

式中：Rerosion为材料表面冲蚀磨损速率，kg/(m2·s)；Nparticles为颗粒碰撞壁面的数量，个；mp为颗粒质量流量，kg/s；C(dp)为颗粒粒径函数，取定值1.8×10-9；θ为颗粒与壁面的冲击角，rad；vp为颗粒碰撞材料表面的速度，m/s；b(v)为颗粒相对壁面的速度函数，取定值2.6；Aface为壁面计算单元的面积，m2；f(θ)为颗粒与壁面的冲击角函数，采用分段多项式函数拟合冲击角函数，将0°、20°、30°、45°和90°的函数值分别设置为0、0.8、1.0、0.5和0.4。

冲缝筛管使用的材料为S13Cr油管钢，适用于I.FINNIE等[21]提出的模型，壁面恢复计算公式为：

(3)

式中：en为法向恢复系数，et为切向恢复系数，无量纲。

2.2 冲缝套流道及缺陷分布

冲缝套的缝道分布均匀，可建立单个缝道的流道，流道出口设置为双缝。冲缝套实物如图5a所示。测量冲缝套单元相关数据，建立冲缝套单元模型，如图5b所示。以缝口上方7.5 mm处为参考面，建立1个包含缝道的长方体，设置长方体为主体、冲缝单元模型为特征，2个模型组合后得到冲缝套流道，如图5c所示。在进行腐蚀缺陷数值模拟时，一般将腐蚀缺陷分布设置为双点腐蚀，腐蚀坑的截面主要为圆形和矩形[22-25]。由图4可知，腐蚀坑截面为圆形，所以将腐蚀缺陷截面设置为直径为1 mm的圆形或半圆。为了探究缺陷位置对冲蚀的影响，缺陷位置分布如图6所示。2种分布方式的缺陷总面积相等，缺陷圆心之间的距离称为缺陷间距z，并且缺陷在zx平面成轴对称分布。缺陷为圆柱或半圆柱，高度为h。图6的间断线是读取冲蚀磨损量的位置，距离出口0.2 mm，长9 mm。将冲缝套底面分为3个区域，中间区域、边缘中间区域和边缘四角区域。

图5 冲缝套建模流程图Fig.5 Process of punched sleeve modeling

图6 腐蚀缺陷分布位置Fig.6 Distribution position of corrosion flaws

2.3 网格划分

采用非结构化六面体网格对2种缺陷模型进行网格划分，并对缺陷部分进行局部加密。网格无关性模拟结果如图7所示。当网格数量超过15万后，2种缺陷模型最大冲蚀速率的结果变化不超过5%，继续提高网格数量并不能获得更高的计算精度，所以使用网格数量为15万左右进行后续计算。2种模型的网格划分结果如图8所示。

图7 网格无关性模拟结果Fig.7 Results of grid independence simulation

图8 模型网格划分结果Fig.8 Results of grid division

2.4 动态数值模拟方法及边界条件

以层铺法(Layering)模拟腐蚀缺陷单向运动过程，网格阈值通过网格高度、坍塌因子和分裂因子控制，分别设置为0.5、0.4和0.3 mm，定义运动面为刚体。

对中间两点缺陷模型进行稳态和瞬态模拟对比分析。瞬态模拟考虑腐蚀对冲蚀的影响，腐蚀速率由动网格速率体现。根据腐蚀试验结果，含水体积分数为0时，腐蚀速率为0.011 5 mm/a，故控制腐蚀缺陷的动网格速率为3.65×10-10mm/s模拟冲缝套受到腐蚀作用。数值模拟设置如下：速度为3 m/s，颗粒直径为0.050 mm，质量流量为0.010 kg/s。瞬态模拟设置时间步长为1×10-6s/步，每计算0.001 s(即1 000步)保存一次数据，每个项目计算0.030 s。瞬态模拟的项目较多，仅给出计算0.030 s的结果云图，其他边界条件如表2所示。

表2 瞬态模拟的边界条件Table 2 Boundary conditions for transient simulation

3 数值模拟结果与分析

3.1 中间两点缺陷模型的计算结果与分析

依边界条件，使用中间两点缺陷模型进行数值模拟。缺陷深度为0.1 mm时，瞬态计算的结果如图9所示。由图9可知，最大冲蚀磨损量为4.613×10-7kg/m2。最大冲蚀磨损量的变化量除以所用时间即为最大冲蚀磨损速率，取0.020～0.030 s之间最大冲蚀磨损速率的平均值作为最终结果，为2.083×10-5kg/(m2·s)。其他缺陷深度时，中间两点缺陷模型的最大冲蚀磨损量变化过程相似。

在0.017～0.019 s之间，最大冲蚀磨损速率出现了阶梯式增长，最大冲蚀磨损量的分布区域从缺陷处变为边缘四角区域。这是因为正对倾斜面射入的颗粒在冲缝套流道中运动距离更长，并且在撞击倾斜面后，对边缘四角区域造成二次撞击。中间两点缺陷对冲缝套的冲蚀影响较小，中间区域不是冲缝套的主要破坏区域。

缺陷深度为0.1 mm时，瞬态计算的冲蚀磨损云图如图10所示。由图10可知，最大冲蚀磨损量为4.614×10-7kg/m2。设置显示的最大冲蚀磨损量为4.100×10-7kg/m2，超过范围的区域不显示，说明此区域受到的冲蚀磨损量更大，称为冲蚀聚集区。冲蚀聚集区分布在边缘四角区域，说明边缘四角区域是易破坏区域。中间两点缺陷使缺陷及其附近区域的冲蚀磨损量增大，说明缺陷是冲蚀的重要影响因素。

图9 缺陷深度为0.1 mm时的瞬态计算结果Fig.9 Transient calculation at the flaw depth of 0.1 mm

图10 缺陷深度为0.1 mm时，瞬态计算的冲蚀磨损云图Fig.10 Transient calculation of erosion wear at the flaw depth of 0.1 mm

中间两点缺陷模型的稳态和瞬态计算结果如图11所示。由图11可知，稳态计算结果大于瞬态计算结果，最大冲蚀速率和最大冲蚀磨损速率之间的差距与缺陷深度呈正相关。缺陷深度0.1 mm时，稳态计算第n步和第m步的冲蚀速率云图如图12所示。由图12可知，设置显示的最大冲蚀速率分别为2.20×10-5和2.00×10-5kg/(m2·s)。稳态结果显示，冲蚀聚集区分布的位置是随计算步数变化的，这两个结果都合理。由于中间两点缺陷模型的结构特点，冲蚀聚集区随计算步数变化随机分布在缺陷处和边缘四角区域，稳态计算的结果与最后一次注入的颗粒有关，颗粒运动的变化导致了最大冲蚀速率变化幅度较大，且分布区域也发生了改变。由图9可知，计算0.020 s后，最大冲蚀磨损速率变化幅度低于2%，瞬态计算结果的可靠性更优。

图11 中间两点缺陷模型的稳态和瞬态计算结果Fig.11 Steady state and transient calculation of the model with two flaws in the middle

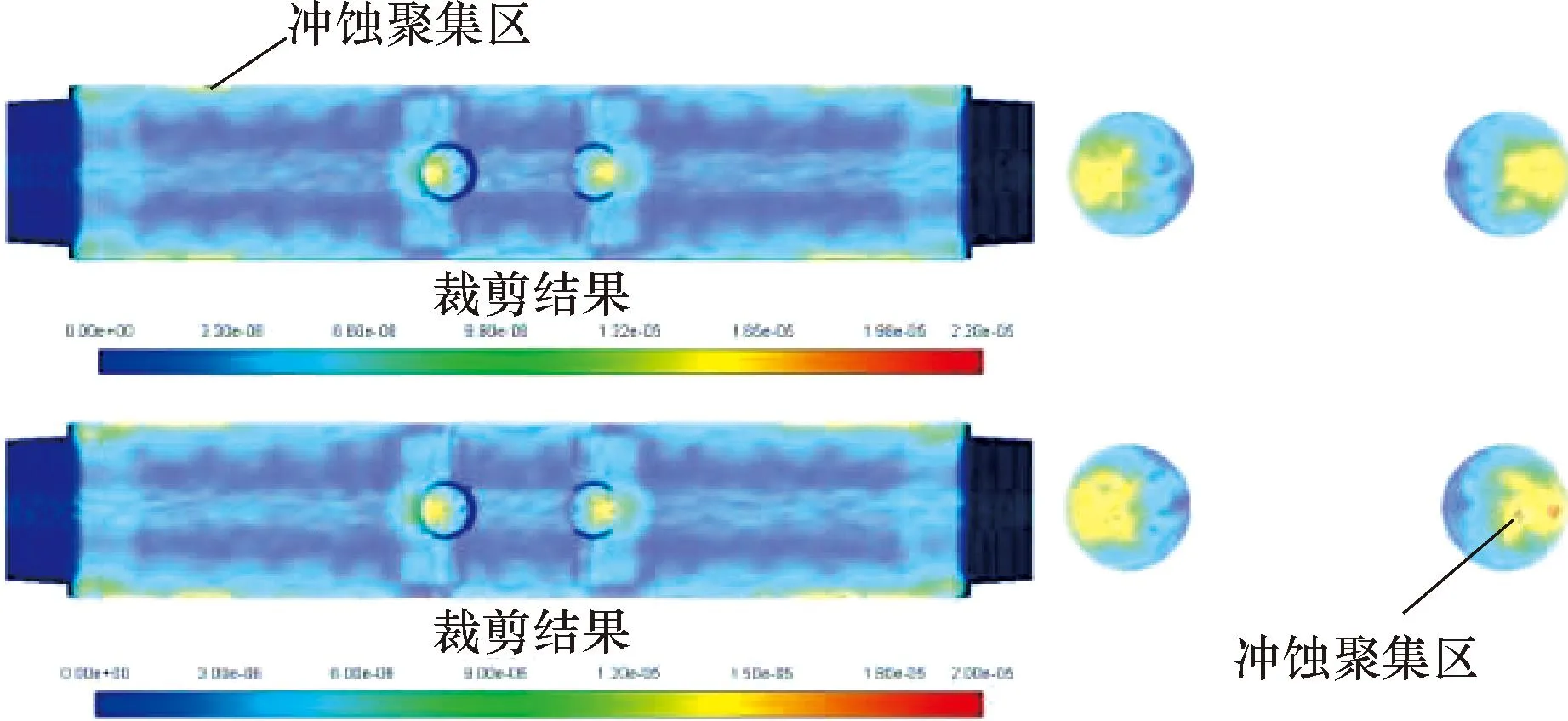
图12 缺陷深度为0.1 mm时，稳态计算第n步(上)和第m步(下)的冲蚀速率云图Fig.12 Erosion rates of the nth (top)and mth (bottom) steps in steady state calculation at the flaw depth of 0.1 mm

3.2 边缘四点缺陷模型的计算结果与分析

3.2.1 缺陷间距对冲蚀的影响

缺陷深度为0.1 mm时，使用边缘四点缺陷模型进行瞬态计算，设置缺陷间距2、9和15 mm，探究缺陷间距对冲蚀的影响。缺陷间距2 mm时，瞬态计算的结果如图13所示。边缘四点缺陷模型的结果取0.020～0.030 s之间最大冲蚀磨损速率的平均值作为最终结果。其他缺陷深度时，边缘四点缺陷模型的最大冲蚀磨损量变化过程相似。不同缺陷间距时，瞬态计算的冲蚀磨损云图如图14所示。缺陷间距2 mm时，最大冲蚀磨损量在缺陷处呈现两点分布，0.030 s累计最大冲蚀磨损量为1.117×10-6kg/m2，最大冲蚀磨损速率为4.245×10-5kg/(m2·s)。缺陷间距9 mm时，最大冲蚀磨损量在缺陷处呈现一点分布，0.030 s累计最大冲蚀磨损量为1.253×10-6kg/m2，最大冲蚀磨损速率为4.954×10-5kg/(m2·s)。缺陷间距15 mm时，最大冲蚀磨损量在边缘最外端，0.030 s累计最大冲蚀磨损量为7.579×10-7kg/m2，最大冲蚀磨损速率为2.898×10-5kg/(m2·s)。

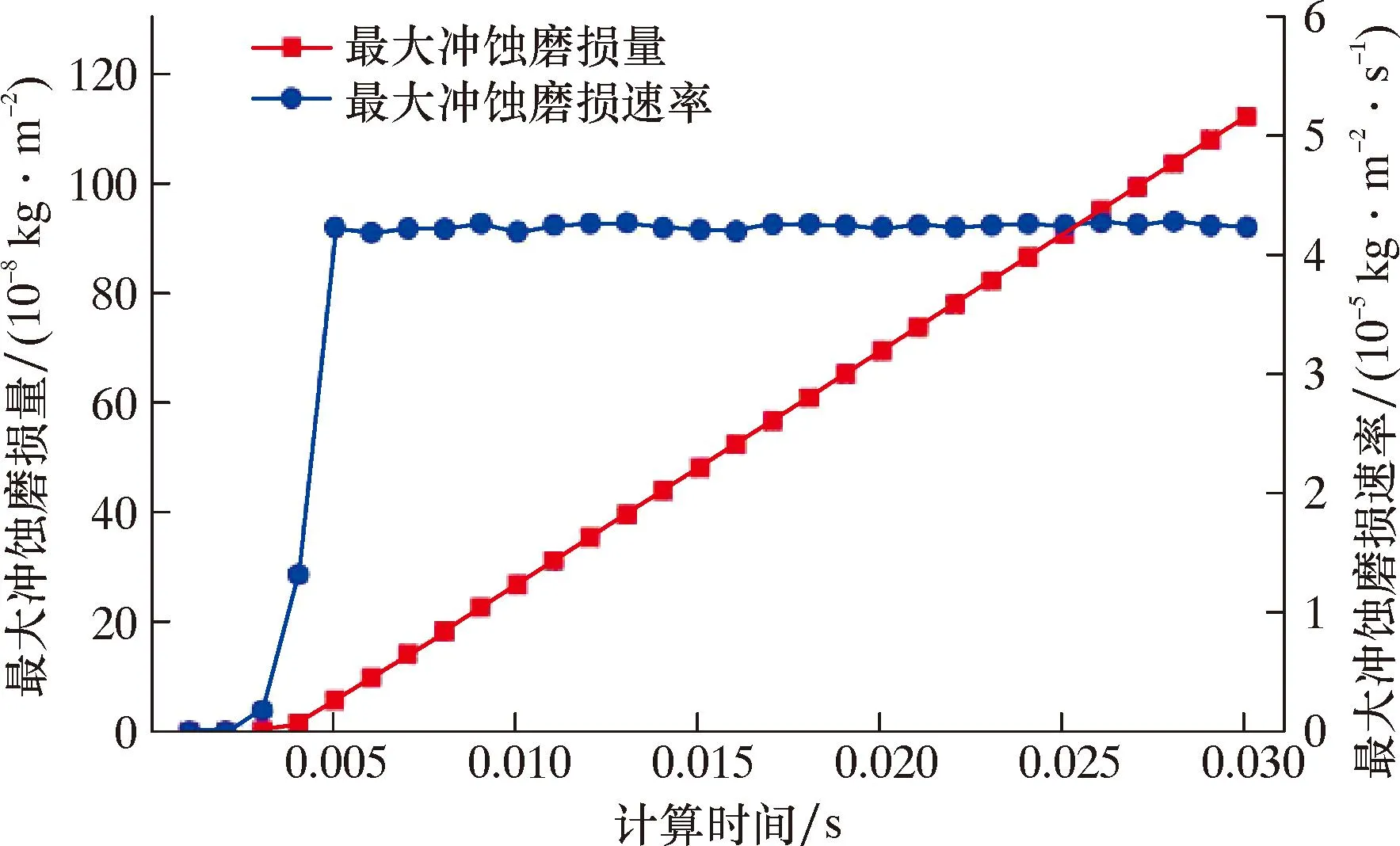
图13 缺陷间距2 mm时，瞬态计算的结果Fig.13 Transient calculation at the flaw spacing of 2 mm

图14 不同缺陷间距时，瞬态计算的冲蚀磨损云图Fig.14 Transient calculation of erosion wear at different flaw spacings

不同缺陷间距时，间断线上的冲蚀磨损量如图15所示。非缺陷区域的冲蚀磨损量成周期性波动，并且波动幅度及周期长度是相同的。由于入口面大于底面，部分颗粒撞击倾斜面后，二次撞击底面，导致8～9 mm段的冲蚀磨损量明显增大。缺陷间距15 mm时，最大冲蚀磨损量分布在8～9 mm段；只有缺陷间距为2 mm时，缺陷部分的冲蚀磨损量大于非缺陷部分；缺陷间距为9 mm时，最大冲蚀磨损量分布在缺陷处，但是缺陷部分整体的冲蚀磨损量明显下降，并且远离底面中心一侧的非缺陷区域冲蚀磨损量大幅增加；缺陷间距为15 mm时，缺陷部分的冲蚀磨损量明显下降。边缘四点缺陷对冲蚀有明显影响，缺陷间距在一定范围内(比如2 mm)，会使缺陷处整体的冲蚀磨损量大幅增加，加快冲缝套的破坏。缺陷间距超过一定范围(比如15 mm)，会使非缺陷部分冲蚀磨损量大幅增加。因此，冲缝套冲蚀磨损最快的部分在边缘中间区域。

图15 不同缺陷间距时，间断线上的冲蚀磨损量Fig.15 Erosion wear amount on the discontinuous line at different flaw spacings

3.2.2 缺陷深度对冲蚀的影响

缺陷间距为2 mm时，使用边缘四点缺陷模型进行瞬态计算，设置缺陷深度为0.1、0.2、0.3、0.4和0.5 mm，其他边界条件相同，探究缺陷深度对冲蚀的影响。含水体积分数为0.5%时，不同缺陷深度的冲蚀云图如图16所示。由图16可知：含水体积分数为0.5%，缺陷深度从0.1 mm增加到0.5 mm时，对应的最大冲蚀磨损量从1.117×10-6kg/m2增加到2.121×10-6kg/m2；缺陷深度越大，最大冲蚀磨损量越大。缺陷深度从0.1 mm增加到0.5 mm，最大冲蚀磨损区域由两点分布向“二”字分布转变，最大冲蚀磨损区域的面积明显增大。不同缺陷深度时，间断线上的冲蚀磨损量如图17所示。由图17可知：缺陷深度越大，非缺陷区域的冲蚀磨损量越小，波动幅度越小；缺陷深度越大，开口高度越大，缺陷处的流量变大，流体携带的颗粒增多，所以缺陷处的冲蚀磨损量就越大。相应的，非缺陷区域的冲蚀磨损量越小。

图16 含水体积分数为0.5%，不同缺陷深度的冲蚀云图Fig.16 Erosion at different flaw depths and 0.5% volume fraction of water

3.2.3 含水体积分数对冲蚀的影响

缺陷间距为2 mm时，使用边缘四点缺陷模型进行瞬态计算，设置含水体积分数为0.5%、1%、2%和4%，探究含水体积分数对冲蚀的影响。缺陷深度为0.1 mm，不同含水体积分数的冲蚀云图如图18所示。由图18可知，含水体积分数从0.5%增加到4.0%，最大冲蚀磨损量从1.117×10-6kg/m2增加到3.750×10-6kg/m2，含水体积分数越大最大冲蚀磨损量越大。含水体积分数从0.5%增加到4.0%，最大冲蚀磨损区域由两点分布向“一”字分布转变，主要冲蚀磨损区域(绿色区域)分布面积明显减小。

图17 不同缺陷深度时，间断线上的冲蚀磨损量Fig.17 Erosion wear amount on the discontinuous line at different flaw depths

不同缺陷深度时，各个含水体积分数的最大冲蚀磨损速率如图19所示。由图19可知：缺陷间距为2 mm时，边缘四点缺陷模型的最大冲蚀磨损速率与含水体积分数、缺陷深度成正比。在含水气井中，随着含水体积分数的增加，腐蚀速率和冲蚀磨损速率增加；冲缝套受到腐蚀和冲蚀产生缺陷，特别是边缘中间区域的缺陷，会使缺陷处受到的冲蚀磨损速率进一步增加。在这种腐蚀和冲蚀的共同作用下，冲缝筛管在含水气井中极易被破坏，缩短服役寿命。

图19 不同缺陷深度时，各个含水体积分数的最大冲蚀磨损速率Fig.19 Maximum erosion wear rate at different water cuts and flaw depths

4 结 论

(1)含水体积分数从0到100%，S13Cr的腐蚀速率从0.011 5 mm/a增长到0.039 9 mm/a。瞬态模拟考虑腐蚀对冲蚀的影响，腐蚀速率由动网格速率体现，动网格速率取3.65×10-10mm/s。

(2)中间两点缺陷模型的稳态结果随计算步数变化，冲蚀聚集区随机分布在缺陷处和边缘四角区域；瞬态结果显示，计算0.020 s后，最大冲蚀磨损速率变化幅度低于2%，瞬态计算结果的可靠性更优。

(3)边缘四点缺陷模型的缺陷间距为2 mm时，最大冲蚀磨损量分布在缺陷处，并且缺陷部分整体的冲蚀磨损量大幅增加，冲缝套冲蚀磨损最快部分在边缘中间区域。

(4)最大冲蚀磨损速率与含水体积分数、缺陷深度成正比。随着含水体积分数提高，冲缝套边缘中间区域受到的腐蚀和冲蚀磨损速率越高，缺陷深度越来越大；随着缺陷深度的增加，缺陷区域的冲蚀磨损速率进一步提高。这种腐蚀和冲蚀的共同作用是冲缝筛管在产水气井中服役寿命大幅缩减的原因。