谈谈带电粒子在磁场中做圆周运动的几种证明方法*

余 超

(广西柳州高级中学 广西 柳州 545001)

1 引言

在当前高中物理学习中,带电粒子在横向磁场中做匀速圆周运动是我们的基本认知.但是无论是从高中教材或是大学物理教材中都可发现,有关的论述都较为粗略,很多学生都知其然不知其所以然.基于此,笔者从深度学习的角度入手,从多角度分析出带电粒子在电磁场中做的是匀速圆周运动并给出合理证明.

2 多角度证明

情境：如图1所示,一质量为m,电荷量为+q的粒子以初速度v0射入与速度方向垂直的匀强磁场中,不计粒子重力,试证明粒子在磁场中做圆周运动.

图1 粒子在磁场中受力图

2.1 曲率半径的角度

如图2所示,粒子所受洛伦兹力与初速度不共线,故粒子在磁场中做一般的曲线运动

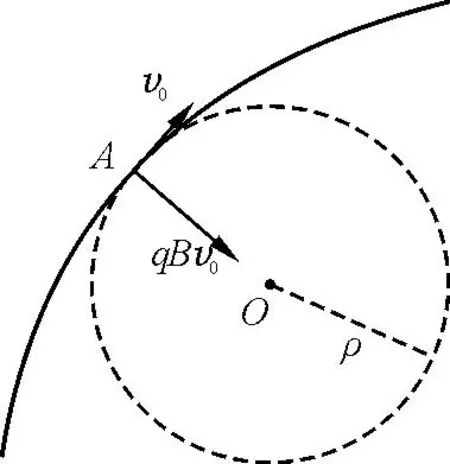
图2 作曲线上A点处的曲率圆

qv0B=ma

设粒子经过某点时做曲线运动的曲率半径为ρ

上式说明粒子做曲率半径不变的曲线运动,即匀速圆周运动.

评析:该角度运用了处理一般曲线运动时的常见思路,即引入曲率半径.尽管这条未知曲线各个位置的弯曲程度可能不同,但在研究时,我们将该曲线分割为许多小段,将A点的这小段看做曲率半径为ρ的圆周运动的一部分,继而证明轨迹为圆周.将研究问题的背景放在了学生已知的情景中,更为直观,容易被学生接受,还加深了学生对曲线运动的认识.

2.2 动量定理的角度

如图3所示建立平面直角坐标系,粒子从O点沿y轴正方向射入垂直纸面的匀强磁场,经一段时间运动到A(x,y)处,在这段运动过程中,对x方向列动量定理方程

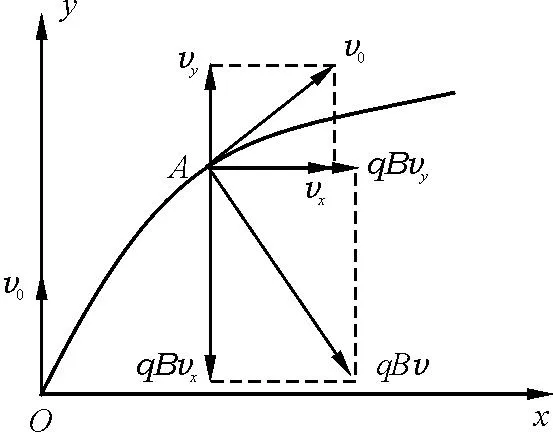
图3 直角坐标系中受力和速度分解图

∑qBvyΔt=mvx-0

即

qBy=mvx

对y方向列动量定理方程

-∑qBvxΔt=mvy-mv0

即

-qBx=mvy-mv0

因f⊥v,力做功Wf=0,则

评析:对大小和方向均变化的洛伦兹力分方向使用动量定理,把整个研究过程分成许多微小的时间段,当段数足够多时,在每一小段时间内,变力就可以近似看作恒力,通过求和得到整个过程中洛伦兹力的冲量,在避开了复杂的积分计算的情况下求得结论.近年高考中运用“微元求和”求解物理量的习题频繁出现,该方法为训练学生对类似问题的处理提供了一个案例,在实际教学中可以加深学生对“微元与求和”思想方法的体会和理解.

2.3 矢量分析的角度

由牛顿第二定律

普洛斯，这家世界物流地产巨头被万科收购，一时间令无数物流人感到意外。本次收购案中，万科及若干其他财团成员为收购设立的联接基金的总出资额约24.54亿美元。普洛斯退市后，万科成为普洛斯的单一最大持有人。

(1)

根据线速度和角速度的关系

v=ω×r

代入式(1)得

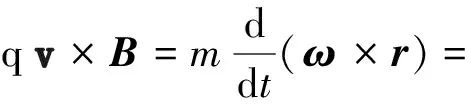
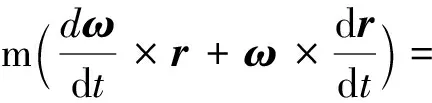
m[(α×r)+(ω×v)]

(2)

因粒子初速度与磁场方向垂直,故粒子所受洛伦兹力在垂直于磁场平面内,并与速度v垂直且共面(图4),因此,粒子运动的角速度ω与线速度v垂直,角加速度α与由圆心指向粒子所在位置的矢量r垂直.再据角量与线量的关系v=ωr和aτ=αr,式(2)可写为

(3)

图4 各矢量方向图

式(3)中en为指向圆心的法向单位矢量,eτ为沿切线方向单位矢量.

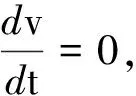
评析:该方法本质上是将粒子的加速度分解成切向和法向两个分量,运用矢量运算的法则,计算得到加速度切向分量为零,从而推导得出粒子角速度恒定,即粒子做匀速圆周运动.为教师在高中物理教学中有效贯彻数理思想提供一种方法和视角.

2.4 极坐标下质点运动学的角度

如图5所示建立极坐标系,则粒子运动的加速度表达式为

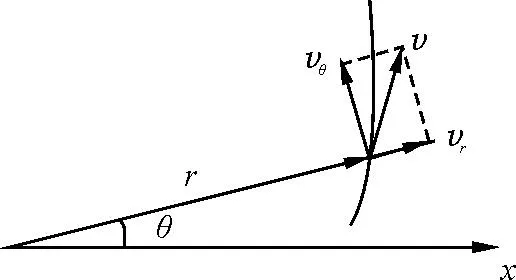
图5 在极坐标系中描述速度

aθ=0

则

因f⊥v,故β必为零,则vr=0,a=ar,有

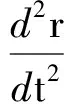
得

评析:运用极坐标系分析粒子的平面曲线运动是物理竞赛中的常用方法,将粒子的加速度分解为横向和径向分量,体会在不同坐标系视角下对运动的描述.让学生对运动的描述有了进一步的理解,同时,也给参加物理竞赛的学生在解决竞赛的相关问题时提供了思路.

2.5 微分方程的角度

如图6建立直角坐标系,对x、y方向分别列动力学方程

(4)

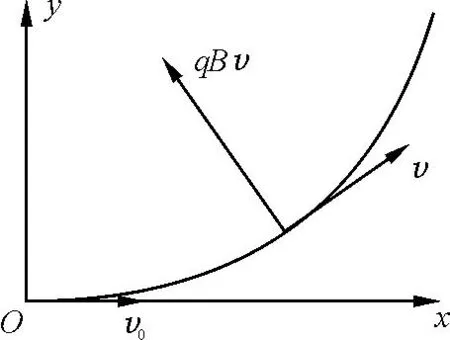
图6 带电粒子受力和速度图

(5)

联立式(4)、(5)得

得

(6)

代入初始条件vy0=0,得φ1=0.

则

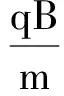
同理得

(7)

对式(6)、(7)两边积分,求轨迹方程

可得

(8)

(9)

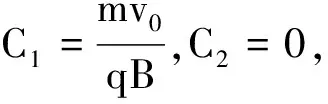
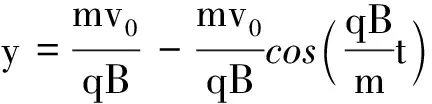
消去t得

评析:本方法采用了大学物理和高等数学的知识进行证明,以一种典型的处理质点运动学的常用思路,即在可以作积分的条件下,给出加速度随时间的变化规律和初速度,便可求速度随时间的变化,进而求解质点运动的运动学方程和轨迹方程.对深入研究物理问题和开阔教师视野提供参考.

3 结束语

本文从深度学习的角度,引导学生对物理问题进行深入思考,5种证明方法由浅至深,从学生的角度看,适应了不同知识水平学生的学习需求,有利于学生拓宽视野、培养科学思维、提升探究能力,让物理学科素养得以落实[1-2].从中学物理教师的角度看,高站位、高观点的视角下看待中学物理问题,在备课和教学中适当运用大学物理的理论、思想、方法剖析中学物理的相关内容,有利于让教师在把握中学物理学科本质和关键的同时提升自身的专业素养.