基于模糊PID控制的点胶单螺杆泵流量控制方法研究

卢梦晨 陈玉* 杨迎娟 王慧明 孟庆洋

(1.安徽工程大学 电气传动与控制安徽省重点实验室,安徽芜湖 241000;2.黄山黄泵单螺杆泵有限公司 产品研发中心,安徽黄山 245000)

单螺杆点胶泵系统具有极高的复杂性,它需要精确地控制,以保证点胶的流量和位置,因此它被广泛应用于精密点胶的领域[1]。螺杆泵主体由一个螺杆和一个阀体组成,通过转动螺杆使得胶水从阀体下方针管中流出,从而进行点胶。由于单螺杆点胶阀的特殊结构,其胶量和胶水流速受到多种因素的影响,如胶水的黏度、螺杆转速等等[2],因此需要一种更加精确的控制方式。

在螺杆泵系统控制领域,国内外对螺杆泵系统控制研究集中在控制模型的建立和系统相关参数的控制。中国石油大学吕清阳在螺杆泵机械式无极调速驱动装置的基础上,采用单片机系统作为控制核心,设计了一套螺杆泵无极调速自动控制系统[3]。吉林大学刘洋利用开环控制方案由驱动控制器向直流微电机两个端子施加不同电压,通过电压幅值高低和时间长短实现转子速度与时间的变化,从而控制螺杆点胶泵的胶液流量[4]。梁辉建立螺杆泵的转速预测模型,利用改进的BP神经网络算法结合PID控制自动调节电机转速[5],提高泵的使用效率和寿命。以上方法虽能很好地控制其被控对象,但大多数方式都为开环控制,控制精度不够,被控对象较为简单,受被控对象本身因素影响过多,无法推广应用到复杂场合。

在工业生产中,精确预测螺杆点胶泵流量是专家学者关注的重点和难点。本文设计了一种模糊PID控制器可以对一些复杂系统进行控制,它不受系统模型的精度影响,可以通过模糊化输入与输出变量和设定适配的模糊规则以达到期望的控制效果。对比传统PID控制其适配性更好,出现干扰时自适应调整能力更强。

1 螺杆泵流量控制系统结构设计

1.1 螺杆泵流量控制系统结构

螺杆泵是一种偏心旋转容积泵,其结构图如图1所示。螺杆泵的流量控制系统结构主要由2、7组成伺服驱动模块,1、3组成流体胶液供给模块,4组成介质输送模块,5组成流量监测模块。控制器接收到微型流量传感器信号,并根据预设流量值通过变频器传达给伺服电机,电机带动螺杆点胶阀内部的偏心转子做行星旋转运动,将胶液输送到针管排出,从而实现点胶。微型流量传感器设置在针管上方,实时监测其内部流量的大小,将流量信号反馈给控制器。此为螺杆点胶泵的一套完整的闭环控制回路。

1.胶液料筒;2.伺服电机;3.胶液导管;4.螺杆点胶阀;5.微型流量传感器;6.固定平台;7.控制器变频器图1 螺杆泵流量控制系统结构图

伺服电机、螺杆泵、变频器、流量传感器,组成了螺杆泵的流量控制系统,如图2所示。给定的系统输入值r(t)与经过数模(DA)转化后的过程变量作差形成误差e,经过控制器处理后,再经过数模转换器把数字信号变成模拟信号送给变频器;通过调整变频器的频率即可改变电机转速,从而控制单螺杆泵的转速。这不仅能够有效调节螺杆泵的流量,更能增加电机和泵的使用周期。采用流量传感器检测出胶头的流量并反馈给系统,利用不断比较输入值与过程变量值之间的误差,通过控制器可以频繁更改转速从而达到校正和控制泵的流量到设定范围内,提高控制精度和速度。

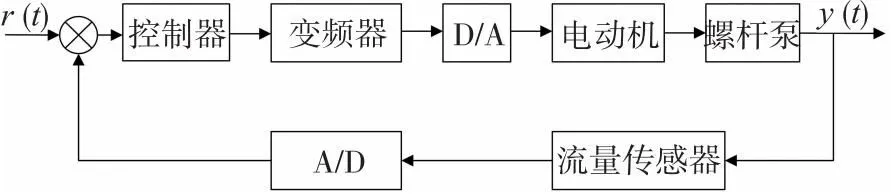
图2 螺杆泵流量控制系统框图

1.2 流量控制系统模型

当多个流量控制环节共同作用于同一管道时,它们之间的相互作用就会产生影响,从而使得整个流量控制系统的稳定性受到严重的破坏[6]。本文把整体系统拆分为两个子系统单独建立模型,这样不仅可以消除互相之间的影响,也会使最后建立的数学模型更加贴近实际情况。

将变频器和电机视作一个完整系统,具有一阶带时滞的惯性系统。其相对应的传递函数为

(1)

其中K1是电机和变频器的增益,T1是变频器和电机的机电时间常量,τ为时滞时间常量。

其余螺杆阀部件可以等效为另一个一阶惯性时滞系统,其相对应的传递函数为

(2)

其中K2是系统的增益,T2是系统惯性时间常量,τ为时滞时间常量。

对于此流量系统可以将两部分合二为一,整合成一个二阶系统,为方便后续控制,将系统理想化,不考虑系统中非线性因素的影响。得到的简化控制模型为

(3)

其中K是系统的增益,T是系统惯性时间常量,τ为系统纯滞后时间常量。

本系统所用的电机为200 W伺服电机,其设计参数如表1所示。

表1 电机设计参数表

一般电机有两个时间常数:机电时间常数Tm和电气时间常数Te。通常Tm>>Te,这种情况下电机的传递函数可看作两个惯性环节的串联,两个惯性环节的时间常数就分别是Tm和Te,而对于一般的应用,由于Te很小,对应的惯性环节可以忽略不计,于是电机的传函就简化为

(4)

当阶跃发生后的Tm时刻,其输出值为0.632。其对应的机电时间常数公式为

(5)

时间常数可通过公式(5)求得,但影响时间常数的因素很多,使得计算出来的数值为近似值。本文通过实际电机测量,空载状态下加上阶跃额定电压,当转速达到空载转速的63.2%时所需要的实际时间[7]。实测电机和变频器机电时间常量T1=0.05,系统惯性时间常量T2=1.03,系统总增益K=1.4,纯滞后时间τ=1.8。将以上数据代入(3)式中,则单螺杆阀流量控制系统近似模型为

(6)

2 流量控制系统稳定性分析

在构建一个控制系统时,除了确保其完全稳定外,还必须确保其具备足够的相对稳定性,以防止由于微小的参数偏差而导致系统性能下降或者失去稳定性[8]。常用的线性定常系统稳定性分析方法有时域分析法、特征根法、劳斯判别法和奈奎斯特稳定性判据,本文采用奈奎斯特稳定性判据[9]对该系统进行分析。

由式(6)可知,该系统为一个比例环节、两个惯性环节和一个延时环节串联而成。可以通过奈奎斯特稳定判据进行稳定性推导。

令s=jω,

(7)

其相角频率特性

ψ(ω)=-arctan0.05ω-arctan1.03ω,

(8)

其幅角频率特性

(9)

当ω=0时:

ψ(ω)=0,A(ω)=1.4,

当ω→∞时:

ψ(ω)=-180°,A(ω)=0,

当ψ(ω)=-90°时:

arctan0.05ω+arctan1.03ω=90° ,
0.05ω1.03ω=1,

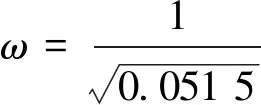
由上述公式推导,可以画出该系统的Nyquist图,如图3所示。其中奈式逆时针包围(-1,j0)点圈数为0圈,即R=0,又因为该系统为最小相位惯性环节系统,所以系统不存在开环不稳定极点,即P=0。

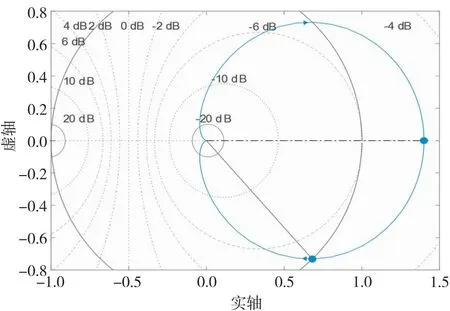
图3 系统Nyquist图

根据奈奎斯特稳定性判据:R=P-Z得出Z=0,该流量控制系统是稳定可控的。

3 点胶单螺杆泵流量控制系统设计

通过使用MATLAB中的Simulink模块对系统进行建模和仿真,研究了不同控制器的优势和局限性,并加入模糊算法进行建模分析,以验证特征参数的优化和整定过程,从而期望获得最佳控制效果,并最终找到最佳控制方案。

3.1 流量控制系统仿真

3.1.1 无优化的流量系统仿真

根据1.2中建立的流量控制系统数学模型,在Simulink中搭建的系统控制模型如图4所示。

图4 无优化流量控制系统模型框图

在本流量控制系统仿真实验中,胶液流量初始输入值是根据具体被点胶对象所需求的点胶量而定的。根据系统特性和目标流量控制阈值,结合实际系统的历史流量数据,给定仿真系统的初始输入值为3,单位为l/h。设置好仿真时间为50 s,系统时滞时间为1.8 s,仿真结果如图5所示。

图5 无优化的流量控制系统阶跃响应图

由图5可知,在无任何优化时,当系统输入值为3时,系统前15 s内发生明显震荡且最终输出值稳定在1.75左右,输入值与输出值相差甚远,控制效果不佳,因此需要引进PID控制算法,以增强系统性能。

3.1.2 传统PID控制流量系统仿真

为了增强系统的性能,对本流量控制系统加入传统PID控制,其模型图如图6所示。

图6 加入PID的流量控制系统模型框图

通过引入传统PID控制后,在不改变原有参数的情况下,通过改变PID控制系统的三个参数环节Kp、Ki和Kd,来提高系统的阶跃响应曲线性能,本文采用经验法对其进行调整,得到系统阶跃响应曲线如图7所示。

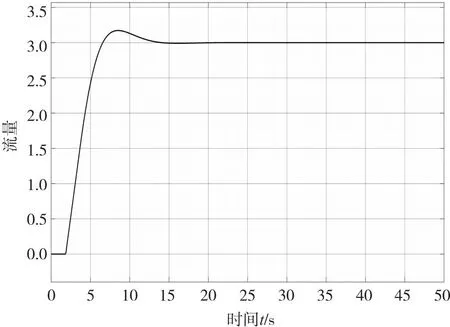
图7 加入PID的流量控制系统阶跃响应图

由图7可知,系统输出信号在10 s前有一段超调,在15 s左右系统达到稳定状态,期望值与输值相等为3。采用传统PID控制的系统可以显著改善系统的性能,但是由于其控制精度和抗干扰能力有限,开机运行时仍然存在较大的振荡和超调,而且到达稳定的用时也比较长,这将对控制器的长期使用造成不利影响。本文旨在应用一种模糊PID控制技术,探索更加精确、稳定的流量控制方法。

3.2 模糊PID控制器设计

通过使用模糊控制,能够处理PID控制器的主要参数,即输入量误差e、变化率ec和输出量Kp、Ki、Kd。这些信息通过模糊控制器进行处理,并通过实时监控来确保控制器的性能。通过这种方式,能够实现更高的控制精度,并且能够根据实际情况进行快速变化。其结构模型图如图8所示。

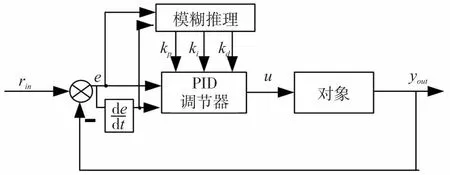
图8 模糊PID控制器结构

在模糊化输入和输出时,需要根据实际情况确定模糊集合的数量和隶属度函数的形状。如果模糊集合数量太少或隶属度函数形状不合理,可能会导致控制精度不高或响应速度较慢。因此,可以通过增加模糊集合数量、优化隶属度函数等方式来改善模糊化输入和输出的精细度。

3.2.1 控制器模糊子集的确定

在模糊控制器设计中,通常就把语言变量的论域定义为有限整数的离散论域[10]。即误差e的论域可以定义为

{-m,m+1,…,-1,0,1,…m-1,m};

误差变化量ec论域定义为

{-n,n+1,…,-1,0,1,…n-1,n};

将输出控制量U的论域定义为

{-l,l+1,…,-1,0,1,…l-1,l};

本文流量控制系统的偏差e和偏差变化ec的论域取{-3～3},输出量Kp的论域取{-0.3～0.3},Ki的论域取{-0.06～0.06},Kd的论域取{-3～3}。其相对应各个部分的模糊子集为7个,分别为正大、正中、正小、零、负小、负中、负大,所对应的语言值为PB、PM、PS、ZO、NS、NM、NS。

3.2.2 确定模糊控制规则和隶属度函数

模糊控制规则是模糊控制器的关键所在,它是由一系列模糊规则和模糊条件语句组成的,即由许多模糊蕴含关系构成。这些条件语句是建立模糊控制器的基础。每一条模糊条件语句都会有对应的模糊蕴含关系,即控制规则。若有n条规则,就把它们表达的n个模糊蕴含关系(i=l,2,…,n)做并连运算 ,则系统总的模糊蕴含关系为

(10)

本文基于Mamdani推理算法[11],结合经验模糊规则制定了e,ec,Kp,Ki,Kp的模糊控制表,共有49条规则,如表2～表4所示。

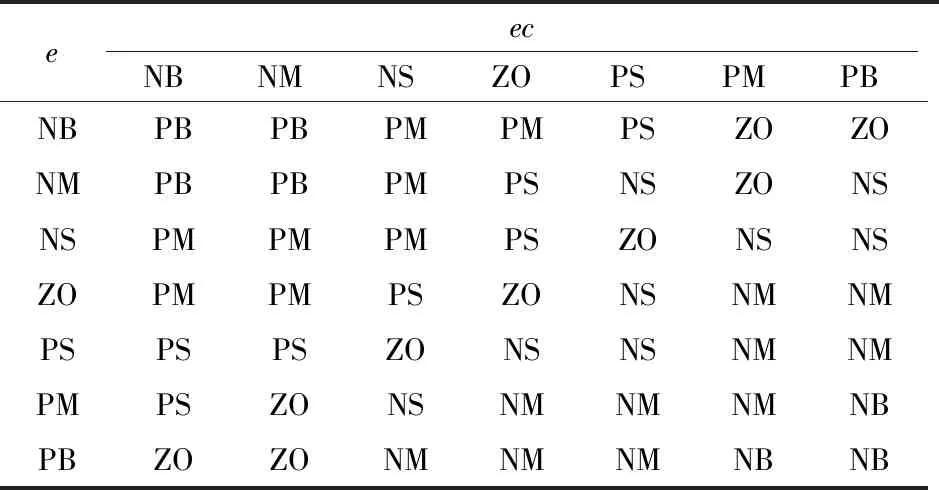
表2 Kp模糊规则表

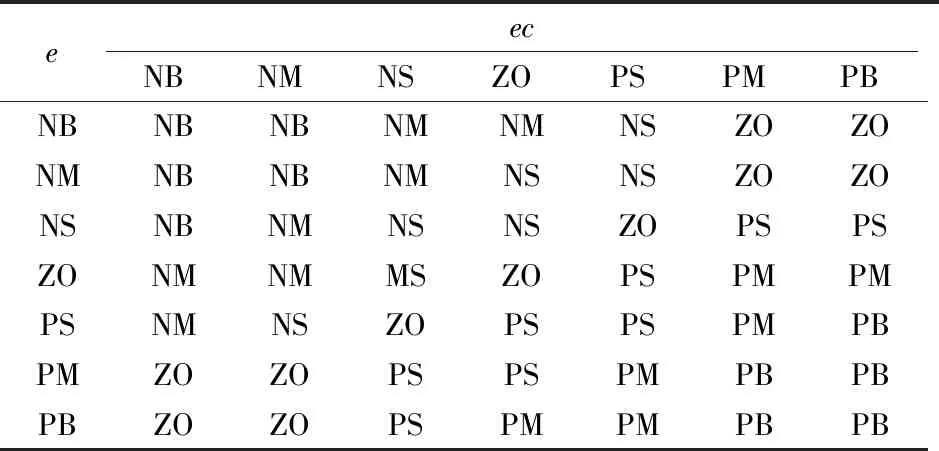
表3 Ki模糊规则表

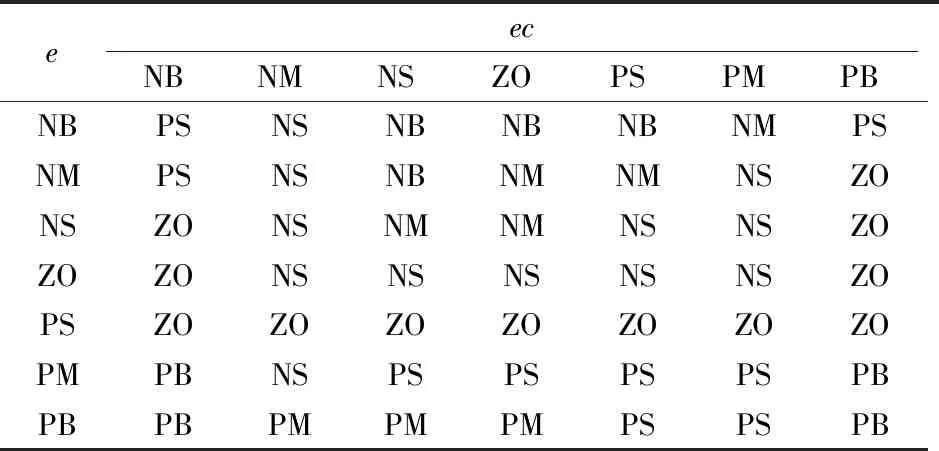
表4 Kd模糊规则表

根据上文确定的e、ec、Kp、Ki、Kd的论域,可以选择运算简单、占用控制器空间较小的三角形隶属度函数,其函数本身形状只与直线斜率相关,适合在线调参的模糊控制。图9～图13分别为其隶属度函数图。

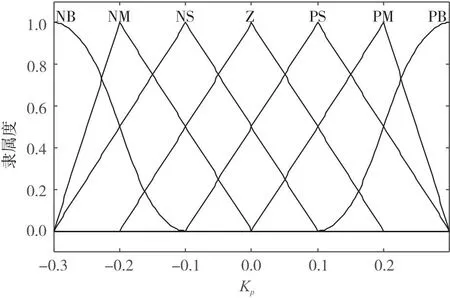
图9 Kp隶属度图

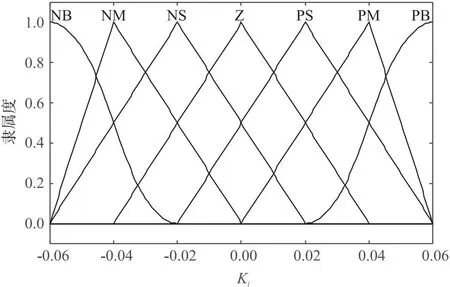
图10 Ki隶属度图

图11 Kd隶属度图

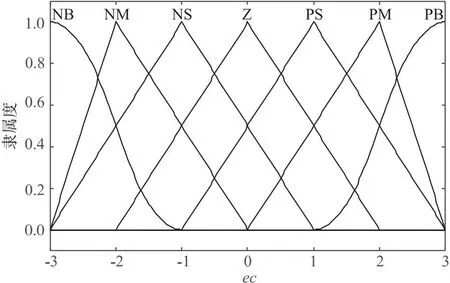
图12 ec隶属度图

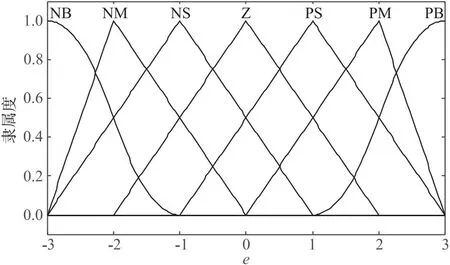
图13 e隶属度图

3.3 加入模糊PID控制系统仿真

在MATLABSimulink软件中搭建流量系统的模糊PID控制模型,选择合适的输入量化因子和输出比例因子。其模糊PID控制器的流量系统模型框图如图14所示。

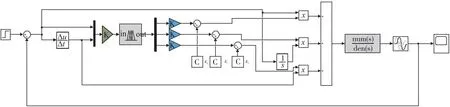
图14 模糊PID控制器模型框图

把模糊PID和传统PID模型放在一起,设置输入信号为3,延时1.8 s,保证比例、积分、微分环节参数一致,调整好模糊PID控制系统输入变量影响因子和输出变量影响因子并进行仿真,其对比效果图如图15所示。点胶机在正常工作时会有周期性,有频繁的启停,螺杆阀腔体内残余的胶液会对下一次点胶周期产生干扰,本文设置25 s为一个点胶周期,加入干扰因素以模拟点胶阀的启停,去验证本控制器是否具有抗干扰能力。如图16所示。

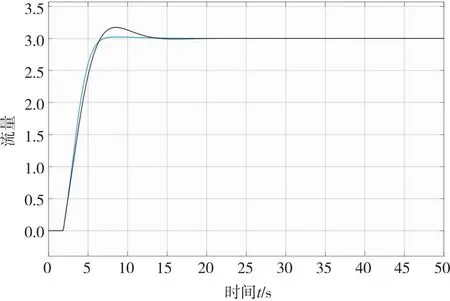
图15 加入模糊PID和传统PID的阶跃响应图

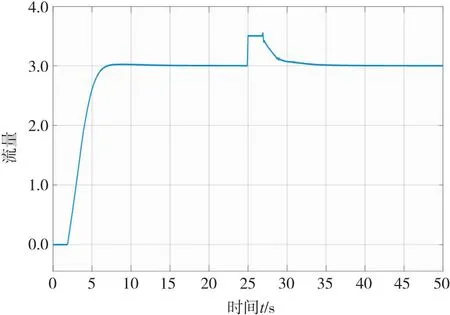
图16 加入干扰信号的模糊PID的阶跃响应图

模糊PID为蓝色曲线,传统PID为黑色曲线。由图16可知,模糊PID控制在6.5 s时达到系统输入值,经过短时间的调整后在10 s左右达到稳定状态。与传统PID控制相比,其响应速度更快,达到稳定状态所需要的时间更短,最重要的是大大减少了系统的超调量。模糊PID控制效果优于传统PID控制,又根据图15,在仿真时间到25 s时给模糊PID控制系统加入一个干扰信号,系统也能在短时间内回调到稳定状态,拥有一定的抗干扰能力。

4 结语

通过对螺杆泵流量控制系统进行分析建模,建立了稳定且可控制的系统模型。运用模糊控制原理建立了系统的隶属度函数和模糊控制规则表,搭建了一种模糊PID控制器。通过仿真实验与传统PID控制方法进行比较,结果显示模糊PID控制较传统PID控制超调量减少了15.1%,上升时间加快了30%,调节时间加快了5.2 s,流量误差在5%以内。模糊PID控制增强了螺杆泵流量系统的稳定性,减小了系统的震荡幅度和超调量,使系统拥有更好的鲁棒性,提高了点胶螺杆泵的性能。