基于双线性ADRC的翼伞系统三维航迹跟踪控制

周宇阳,赵敏,王成,齐贺轩

(南京航空航天大学 自动化学院,江苏 南京 210016)

0 引言

目前常用的充气式翼伞充气后呈现出飞翼的形状,飞行过程中翼伞保持刚性,所以翼伞系统具有良好的控制性能。在飞行过程中,翼伞系统依靠较高的升阻比及优良的滑翔能力,可以实现远距离的投放与定点,精确着陆至现有的常规运输手段难以应对恶劣的地形环境,同时相比于其他的空运方式,翼伞系统具有高负载的优势,以上优势使得翼伞系统在航空航天、军事和民生领域有很好的应用前景[1-3]。

在翼伞系统精确空投领域,导航、制导与控制研究的一个重点是翼伞系统航迹跟踪控制技术[4-6],航迹跟踪得越准确,最终着陆的误差越小。与常见飞行器不同,翼伞系统是一个常见的欠驱动系统,飞行过程完全依靠后缘两侧的襟翼来控制。与此同时,翼伞系统又是一个耦合系统,襟翼的偏转不仅会影响翼伞系统横向气动特性,还会影响纵向气动性能。这些对于控制精度都会有影响,并且翼伞系统是一个非线性系统,系统输入量与输出量不是简单的线性关系。以上3种特性对于翼伞系统的航迹跟踪控制都带来了挑战。

翼伞航迹跟踪控制主要涉及两个方面的研究,其一是制导律的确定。实现翼伞系统三维航迹跟踪控制,要同时满足侧向及纵向的控制要求,这就必须制定合理的侧向和纵向制导律以满足跟踪需要。另一个方面是航迹跟踪控制器的设计,翼伞系统欠驱动、耦合以及非线性的特点导致其控制带来了一定的挑战。

本文以滑翔比为3的翼伞作为研究对象,提出一种新的翼伞系统航迹跟踪控制框架,采用自抗扰控制策略实现无动力翼伞三维航迹跟踪,使其达到航迹跟踪与精确着陆。

1 翼伞6-DOF模型

目前常见的翼伞系统模型主要包括质点模型、6自由度刚体模型及9自由度模型。在解决航迹问题时不需要考虑伞体与载荷之间相对运动,6自由度模型将翼伞系统视为一个整体,包括代表翼伞系统位置的3个平动自由度和表示系统欧拉角的3个转动自由度[φc,θc,ψc]T,质点模型相比之下过于简单,所以本文采用6自由度模型。翼伞6-DOF模型有以下5点假设[7]:

1)翼伞充气后翼型基本保持不变,且沿展向对称;

2)伞体与载荷相对位置固定,不存在相对运动,翼伞系统可以被视为刚体;

3)载荷密度足够大,在空气中运动产生的升力小至可以忽略,只考虑阻力;

4)伞体质心和伞绳对伞体拉力的等效作用点重合;

5)大地为平面。

本文所涉及的翼伞系统受力如图1所示。

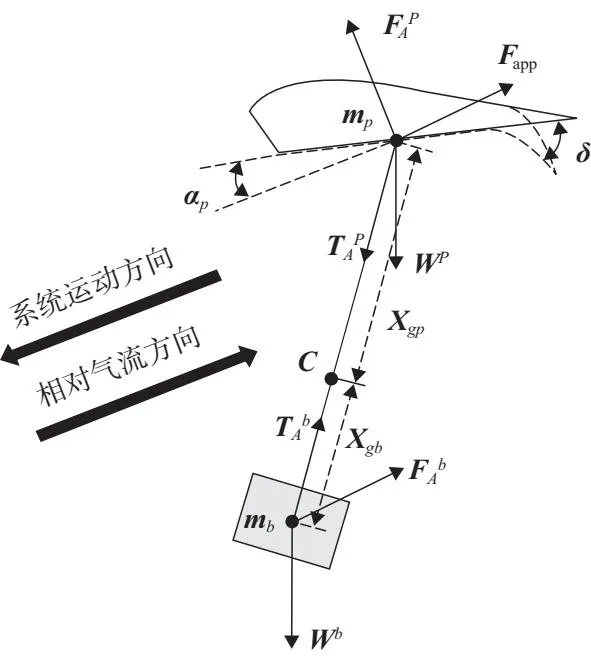
图1 翼伞系统受力示意图

根据受力情况,翼伞6-DOF模型如式(1)所示。

(1)

翼伞控制量为δs和δa,分别是对称襟翼偏转控制量和非对称襟翼偏转控制量。

(2)

式中δLeft和δRight分别为翼伞系统左右两侧后缘襟翼下偏量。

2 航迹跟踪制导率设计

对于翼伞系统而言,制导是指导引和控制翼伞系统按一定规律飞向目标或预定轨道的技术和方法,这种规律即被称为制导律。要实现三维轨迹跟踪控制必须首先确定航迹跟踪制导律,包括侧向制导律以及纵向制导律。

首先,侧向航迹L1制导率[8]原理示意图如图2所示。

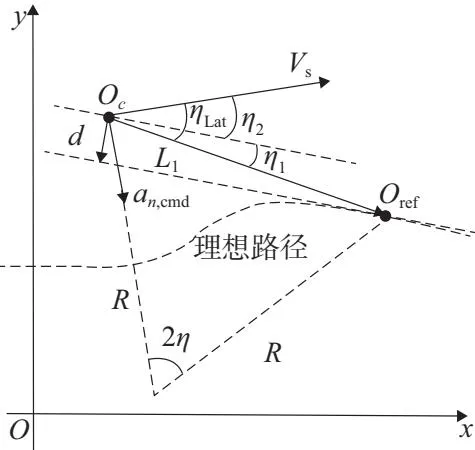
图2 侧向航迹跟踪制导示意图

图2中Oc为翼伞系统质心位置;Vs为翼伞系统水平速度;Oref为理想轨迹上的一个动态移动的参考点;Oc与Oref之间的水平距离为L1(此即为该制导律名称的由来);Oc与Oref连线与Vs的夹角为ηLat。根据牛顿运动定律可知,翼伞沿着半径为R的圆弧轨迹跟踪到参考点Oref所需要的法向加速度为

(3)

可以将图2中系统模型描述为以下运动学公式:

(4)

定义李雅普诺夫(Lyapunov)函数:

(5)

此函数是正定的,从图2可知:

(6)

将式(6)代入式(5),则李雅普诺夫函数可进一步写为

(7)

将李雅普诺夫函数对时间求导可得:

(8)

将式(4)代入式(8),可得:

(9)

接下来是纵向航迹跟踪制导,在垂直面内,主要误差存在于与理想航迹之间的下滑角误差,纵向航迹跟踪制导示意图如图3所示。

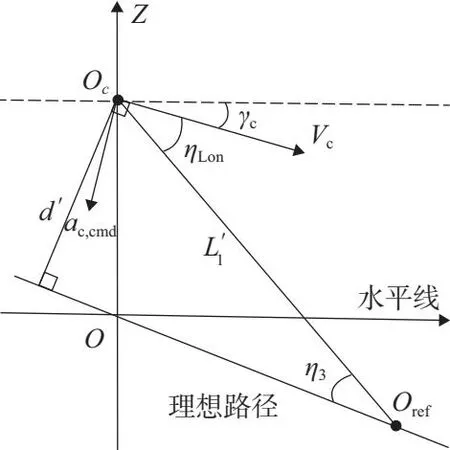
图3 纵向航迹跟踪制导示意图

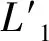
(10)

通常情况下,纵向加速度指令并非沿d′方向,往往需要将其转换为沿d′方向,根据几何关系,有

al,cmd=ac,cmdcos(η3-γc)

(11)

通过控制器控制翼伞系统跟踪理想下滑角输出即可实现对纵向误差的消除,从而实现纵向的轨迹跟踪。

3 B-ADRC控制器设计

在确定制导律后,需要设计相应的控制器来控制翼伞系统弥补误差跟踪理想轨迹。B-ADRC控制器[9]在水平面与垂直面内都可对翼伞系统进行控制,在两个平面内的设计有所不同,首先在水平面内,L1制导律要求飞行器尽可能跟踪理想法向加速度实现路径跟踪,对于翼伞系统6-DOF模型而言,其法向加速度可以表示为

(12)

式中:ψc为翼伞系统航向,为了方便解算,对ψc进行如下处理。

(13)

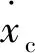
(14)

式中:f1(·)为与系统状态量有关的表达式;f2(ua)为与控制量有关的项;ωdis1为外界干扰(主要为环境风场干扰)。为了方便设计控制器,可以将式(14)进一步改写为

(15)

式中f=f1(·)+f2(ua)+ωdis1-ba0ua。

建立如下扩张状态观测器ESO方程:

(16)

通过扩张状态观测器,可以将翼伞系统法向加速度、加速度的微分及系统总扰动估计出来。采用PD反馈控制律来消除误差,形式为

ua0=kp(an,cmd-z1)-kdz2

(17)

式中:kp、kd根据设定的ADRC控制器带宽来确定;an,cmd为根据L1制导律计算得到的理想法向加速度,非对称襟翼偏转控制输入量为

(18)

由于δa范围有限,必须对其进行饱和限幅处理如下:

(19)

式中δa,max为可以施加的最大非对称襟翼偏转控制量,当控制量输入超过δa,max时,翼伞系统会失速。

在垂直面内,B-ADRC控制器在ESO估计出扰动并补偿完成后,与PD控制器相似,根据上文提出的纵向高度轨迹跟踪制导律的原理,要实现对理想的纵向高度的跟踪,需要控制翼伞系统跟踪理想下滑角输出,翼伞系统下滑角的表达式为

(20)

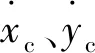
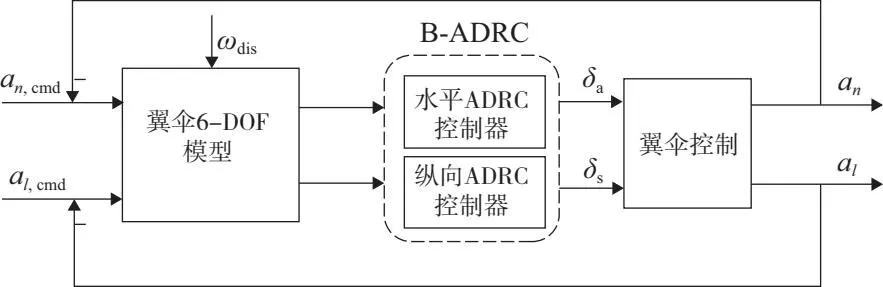
图4 航迹跟踪控制结构

4 实验结果

4.1 仿真实验

结合MATLAB/Simulink构建仿真模型,初始条件见表1,降落点设为坐标原点,着陆点处风向沿大地坐标系x轴正方向,翼伞系统迎风着陆。

表1 初始条件

根据规划的航迹,利用法向加速度误差与下滑角误差设计的控制器进行了轨迹跟踪实验。实际投放点设为(900,1 050,1 650)。翼伞的特性参数和控制器的系数bo、ωo和ωc如表2所示。

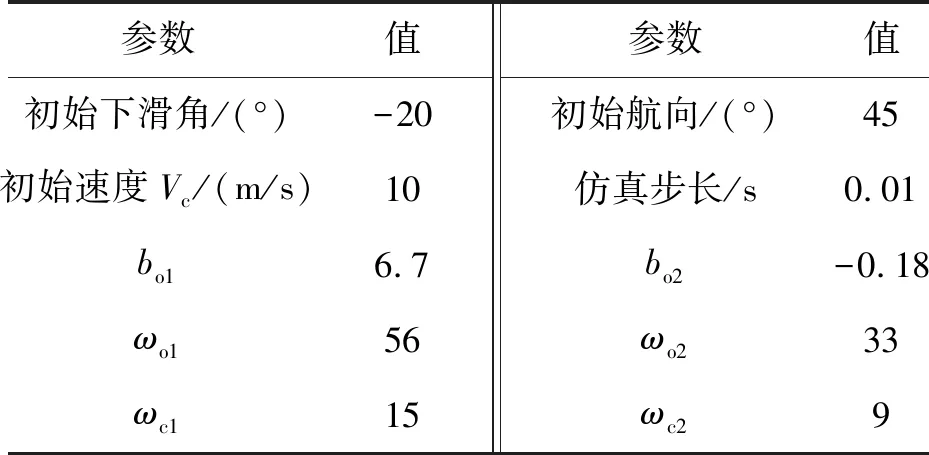
表2 翼伞特性参数以及控制器参数

除了考虑初始位置的偏差外,进一步考虑了随机风的干扰,在200～250s内引入均值为0m/s,均方差为1m/s的随机风场干扰来模拟实际环境中的干扰。

B-ADRC控制下得到的翼伞系统飞行轨迹如图5所示(本刊黑白印刷,相关疑问咨询作者)。可以看出,即使翼伞飞行的初始位置、初始航向角、初始下滑角均存在偏差,但翼伞系统经过较短时间的调整,很快就跟踪上了理想航迹。图5中明显可以看出由于随机风干扰的影响,翼伞飞行轨迹发生明显的波动,但路径很快被调整过来,依旧实现了对理想航迹的跟踪。

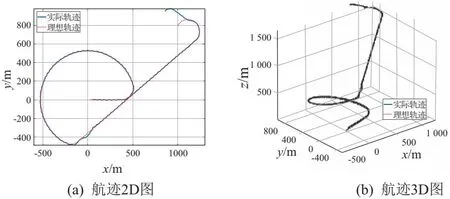
图5 轨迹跟踪控制仿真实验图

跟踪过程中的横向误差以及纵向误差随时间变化曲线如图6所示。

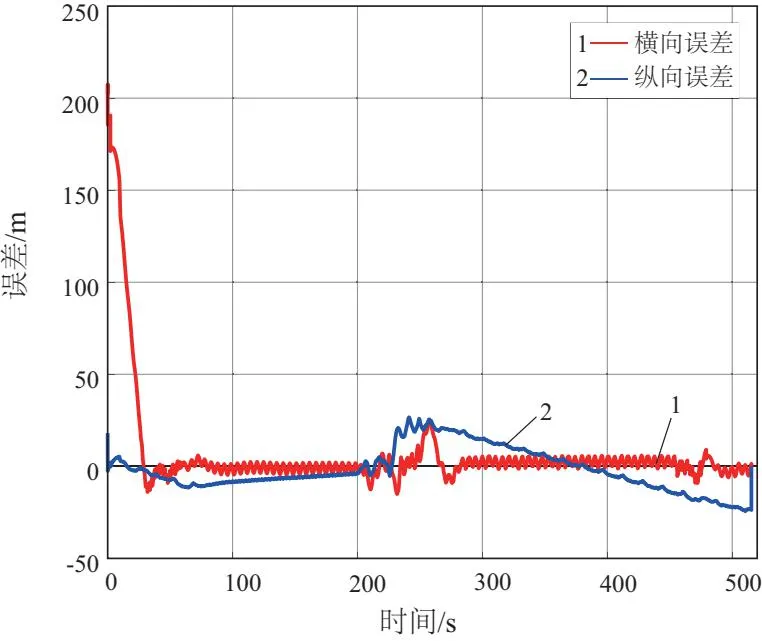
图6 轨迹跟踪误差随时间变化曲线图

根据跟踪误差对时间变化的曲线图可以明显看出,在受到环境风影响发生偏差时,在本文设计的B-ADRC控制器作用下可以迅速调整,把误差控制在合理范围内。观测器的观测值随时间变化如图7所示。

图7 观测器的观测值

4.2 翼伞飞行实验

利用滑翔比约为3的翼伞,构建物理实验平台,进行飞行,实验验证本文方法。图8所示为翼伞飞行状态。如图9所示,在环境有微风干扰的前提下,翼伞依然能够平稳地跟踪理想轨迹并完成逆风着陆。从总体上考量,本文提出的轨迹跟踪算法能够实现三维航迹的跟踪。

图8 翼伞飞行状态图

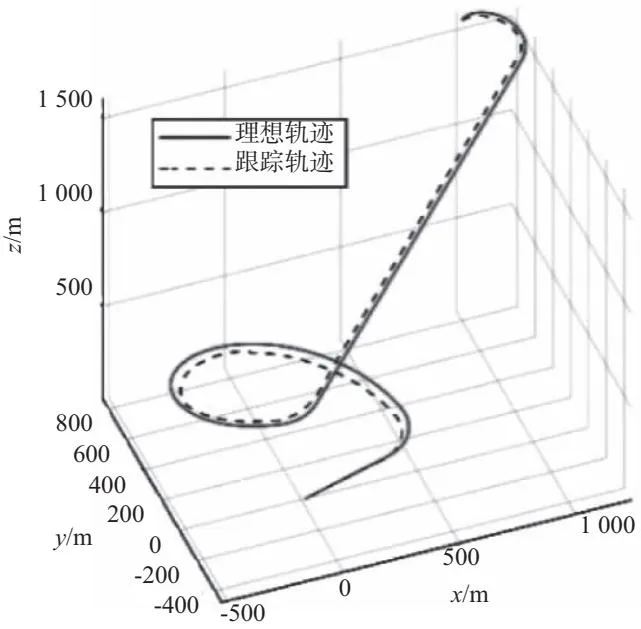
图9 飞行实验轨迹图

5 结语

本文针对翼伞系统三维航迹跟踪提出了一种控制方法,轨迹跟踪控制由两部分组成,分别为轨迹跟踪制导律以及轨迹跟踪控制器的设计。针对6-DOF翼伞系统,在水平轨迹跟踪方面,将L1制导律应用在翼伞系统水平轨迹跟踪,在纵向轨迹跟踪方面,设计了一种结合了高度误差和下滑角误差的方法来确定系统理想下滑角。控制器设计方面,设计了B-ADRC控制器来实现对理想法向加速度以及理想下滑角的跟踪,进而实现对三维轨迹的跟踪。实验证明本文的算法成功实现了对于分段航迹规划理想路径的三维跟踪,且对于过程中的随机风场干扰也能快速适应。