空气涡轮起动机异常振动诊断的STFT分析

熊欣,乔思佳,朱钰珏,蒋聪,任悦,臧朝平

(1. 中国航空工业集团有限公司金城南京机电液压工程研究中心,江苏 南京 211106;2. 空军装备部驻南京地区第三军事代表室,江苏 南京 211106;3. 海军指挥学院 外训大队翻译室,江苏 南京 210016;4. 南京航空航天大学 能源与动力学院,江苏 南京 210016)

0 引言

空气涡轮起动机(air turbine starter, ATS)属于飞机第二动力系统,主要负责带转发动机,使发动机达到稳定工作状态。在高温、高转速的苛刻运行条件下,空气涡轮起动机易产生异常振动。涡轮转子是起动机的核心部件,相较于航空发动机转子,其转速更高,转动惯量更大,一旦振动异常会引发转子破裂等极端情况,高能、高速的碎片可能会击穿包容结构,破坏飞机的集成电源、液压管路等,严重危及飞行安全[1]。

该型空气涡轮起动机由转子系统和壳体系统组成,其中,涡轮转子及齿轮系统组成的减速传动机构是最主要的振动源。在产品交付前,起动机需要先后通过磨试、检试、质检三道实验流程以确保其达到出厂要求。试验中时常因振动幅值偏大出现产品异常振动的情况,偶尔甚至出现涡轮碰磨、输出轴断裂、内部异常磨损等故障现象[2],严重故障时起动机无法运转,进而使航空发动机无法起动。起动机的工作过程是持续的升速过程,无恒转速工况,呈现明显的时变特性。虽然目前国内对于空气涡轮起动机动力学特性、故障模式以及剩余寿命已有许多研究[3-5],但对于起动过程中的时变特征仍需进一步研究。因此建立空气涡轮起动机在变转速工况下的异常振动诊断分析方法就尤为重要。有多种时频分析方法可用于非平稳振动信号的分析,如短时傅里叶变换、希尔伯特-黄变换、小波分析等[6]。其中,短时傅里叶变换由于其简单、高效,在各工程领域得到了广泛应用[7-10]。本文采用短时傅里叶变换对起动机交付前的试验中正常状态及异常状态实测数据进行对比分析,从异常状态的时频谱表现对导致振动异常的原因进行诊断分析。

1 空气涡轮起动机振动信号分析方法

1.1 短时傅里叶变换

在对旋转机械的振动信号进行分析时,通常采用基于傅里叶变换的功率谱密度指标对振动水平进行评估,但对空气涡轮起动机而言,其工作过程为持续升速过程,伴有非平稳特征。傅里叶变换仅能展现定转速稳态工作时的振动信号频域特征,无法应用于时变过程的振动特征提取。为解决此问题,本文采用加窗的傅里叶变换,即短时傅里叶变换(short time fourier transform, STFT)对起动机的时变振动信号进行处理。通过在信号上添加滑移时间窗,对信号进行分段采样,对每组信号进行局部的傅里叶变换。短时傅里叶变换的定义为[10]

(1)

h(t)为窗函数,其值为1时,短时傅里叶变换还原为傅里叶变换。对于给定的时间t,STFT(t,f)可看作是该时刻的频谱,它的时间分量对应于窗口在平移过程中其中心所处的各个位置。每个不同的时间均可获得一个独立的频谱,能够反映该时刻的信号特征,称之为切片谱。

窗函数的类型及窗的宽度对短时傅里叶变换的分析结果有显著影响,常见的窗函数类型有矩形窗、高斯窗、海明窗等。受海森堡测不准原理的制约,窗函数的时宽和带宽无法同时达到任意小,因此无法在时间分辨率和频率分辨率上同时达到最优解[11]。

在Matlab中对振动信号进行分析时,采用spectrogram函数绘制短时傅里叶频谱图,给定信号、窗函数、fft点数以及采样率的情况下,能够输出信号的能量谱密度(PSD)。为得到能够反映主要频率特性的频谱图,需要根据信号特征对窗函数进行选择并进行滤波。根据起动机起动过程的信号特征以及采样频率,选择窗函数类型为海明窗,窗宽度为1 000,为滤除背景噪声,将频谱中PSD值小于最大值15%的频率成分进行滤除。

1.2 空气涡轮起动机结构及常见故障

空气涡轮起动机由转子系统和壳体系统组成。转子系统主要由涡轮转子、齿轮系统(包括主动齿轮、双联齿轮以及环形齿轮等)和轴承组成;静子系统主要由导向器壳体、进气壳体、涡轮壳体、安装壳体、轴承座以及密封座衬盖等部件装配组成。

近10年的空气涡轮起动机维修数据表明,异常振动主要来源于起传动作用的转子系统,如图1所示。高频振动出现的故障有以下几种:输出轴断裂、涡轮失稳碰擦、内部异常磨损等。不同的故障会在频谱上表现为不同的部件转动频率或啮合频率。以涡轮转频为1倍频,该型空气涡轮起动机转子系统各个部件的转动频率和齿轮啮合频率见表1。

表1 转子系统各部件转频及啮合频率

图1 转子系统

1.3 空气涡轮起动机振动信号分析流程

通常,对空气涡轮起动机进行振动监测时,采用低通滤波的方式保留2 000Hz内的振动信息,使用时域加速度谱线来进行异常振动的识别[2]。这种判断方式能够有效识别转子不平衡导致的异常振动,但是由于进行了低通滤波,高频的振动信号如齿轮啮合频率或涡轮转频的高次谐波难以体现。本文分析振动监测时,不作低通滤波处理,以便保留高频振动的信息,信号分析流程如图2所示。在对加速度响应数据做短时傅里叶变换后,通过滤除振动能量较低的成分(PSD值≤0.15×PSDmax值)以去除背景噪声,保留主要振动频率成分,得到改进的短时傅里叶时频谱,同时在重点关注的转速区间做切片谱。将正常状态和异常状态的短时傅里叶时频谱和切片谱进行频率成分的对比分析,从而实现异常振动的成因分析。

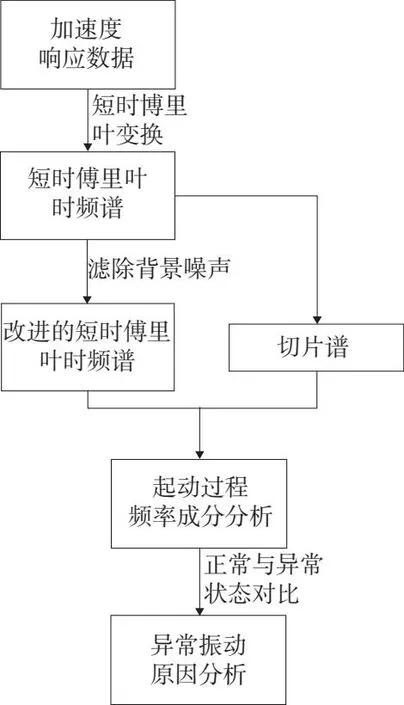
图2 振动信号分析流程

2 空气涡轮起动机起动过程异常振动的短时傅里叶变换分析

振动响应数据采集于空气涡轮起动机的涡轮壳体上,采用加速度传感器,布置位置如图3所示,采样频率为25 600Hz。

图3 加速度传感器布置位置

以某次质检试验中测得的正常工作状态响应数据为例,说明信号分析流程,试验过程共持续28 s,涡轮从0加速到约79 500r/min。其加速度响应原始数据如图4所示。

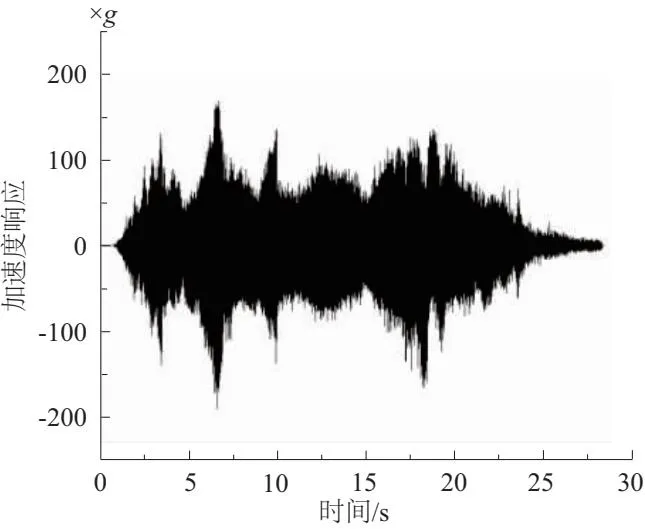
图4 加速度响应信号

采用窗长度为1 000的海明窗,得到短时傅里叶时频谱如图5所示,此时的时频谱频率成分杂乱,仍需进一步处理。

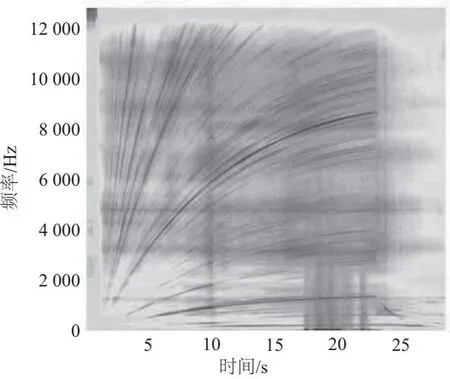
图5 短时傅里叶时频谱

在保留高频振动频率成分同时滤除背景噪声,对振动数据进行如下处理。

1)仅截取涡轮转速升至12 000r/min以上的时频谱,对无振动异常的低转速区不做重点关注。

2)滤除振动能量谱密度低于主要频率成分15%的频率成分。

经处理的短时傅里叶时频谱如图6所示,以涡轮转频为1倍频,7种主要频率成分信息见表2。

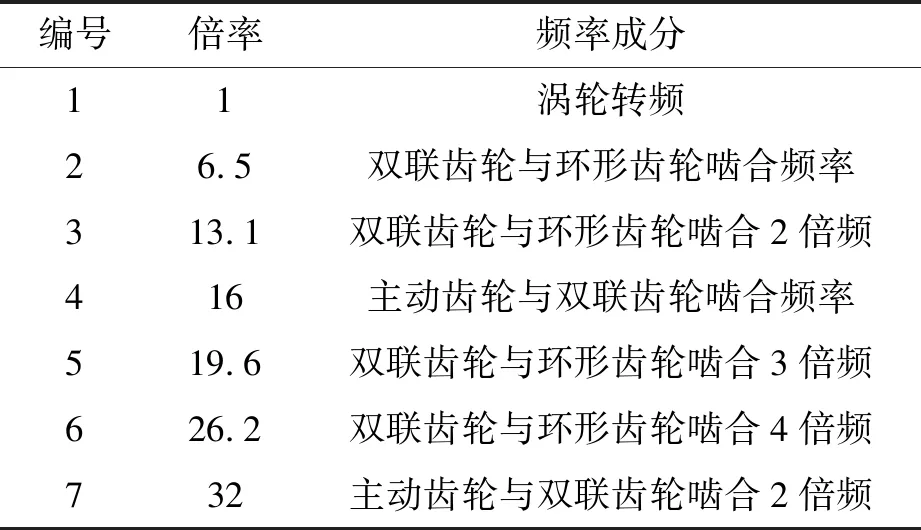
表2 频率成分

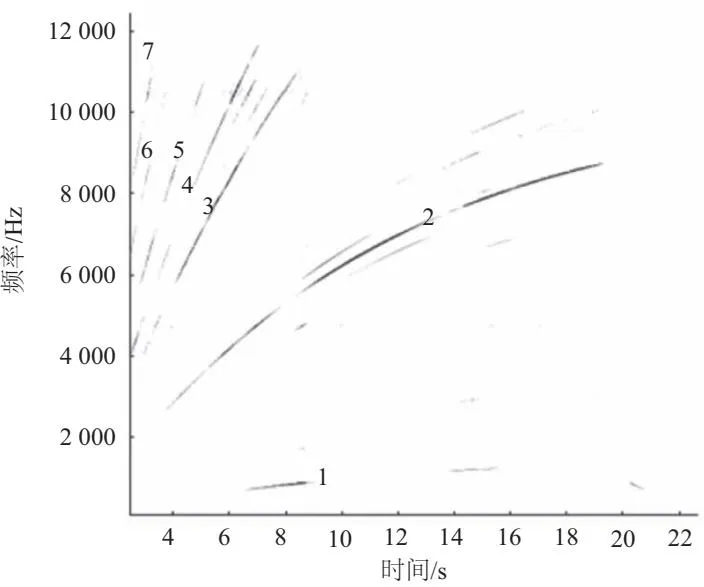
图6 改进的短时傅里叶时频谱

在时域谱中加速度较大的时刻做局部频谱,即切片谱,对产生振动的原因进行分析,各转速下的切片谱及主要频率成分在图7和表3中给出。

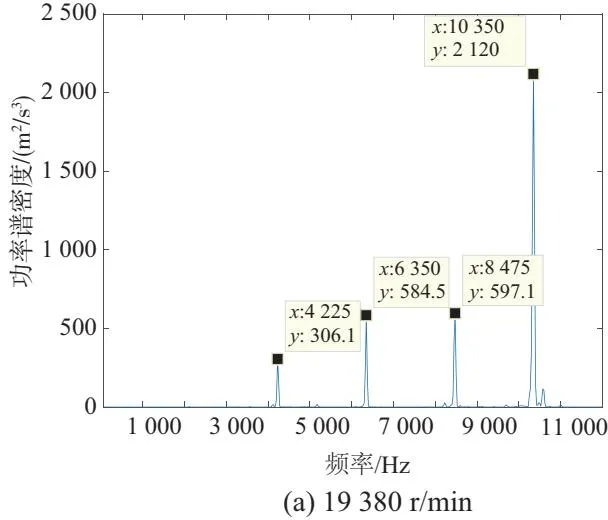
图7 空气涡轮起动机升速过程的切片谱

对其他12次正常工作状态试验数据采用相同的分析方法,进行正常工作状态规律总结:

1)涡轮转速在以下4个区间时,振动响应出现局部峰值,27 000～31 000r/min,37 500～43 000r/min,49 000～59 000r/min,59 000r/min～最高转速;

2)在较低转速区间能够采集到大量的齿轮啮合及倍频成分;

3)涡轮转速在49 000～59 000r/min区间内时,转子过临界转速,可能出现涡轮转频响应,在超过此转速范围后,涡轮转频响应大幅度减弱,如无明显涡轮转频,则主要频率成分为双联齿轮与环形齿轮的啮合频率;

4)涡轮转速升至59 000r/min以上后,双联齿轮与环形齿轮的啮合频率占主导。

在试验流程中,有两次试验出现明显的振动异常,其时频谱如图8所示。

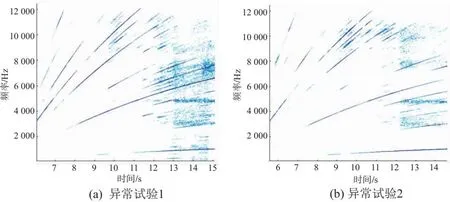
图8 异常状态时频谱

将异常状态的时频谱进行局部放大,如图9所示。

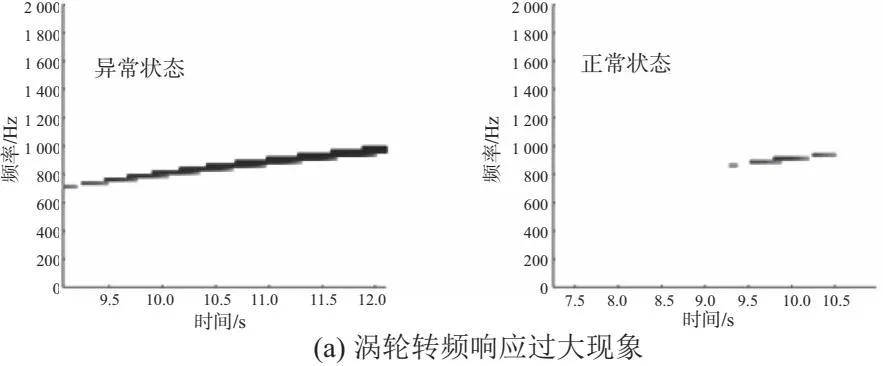
图9 异常现象

从时频谱及切片谱的对比分析中能看到,振动异常状态的时频谱中涡轮转频响应明显或伴随出现涡轮转频高次谐波。针对这两种异常现象分析如下。

1)涡轮转频响应明显,且与转速平方呈正相关:转子在产生不平衡时,理论上离心力与转速的平方成正比。但在转子到轴承、轴承到壳体的振动传递路径上,存在轴承与转子的接触非线性以及连接非线性的影响,壳体上测得的振动随转速的增加而加大,不一定与转速平方完全成正比。

2)伴随涡轮转频的3倍频、4倍频及非整数倍频的谐波:通常研究认为,若3倍频处峰值最大,预示轴与轴承间存在松动;若4倍频处有峰值,表明轴承本身松动。同时松动也可能表现为转子的半周期倍频,如2.5倍频等。起动机在运行一段时间后,可能会由于轴径磨损、轴承间隙过大、装配偏差等原因产生松动。根据试验经验,存在振动异常时将起动机进行拆解再装配时,能够降低振动幅值。在拆解再装配的过程中,有时并未更换部件,或仅调换波浪圈来改变涡轮上角接触球轴承的预紧力,这也验证了振动异常可能来自于装配的偏差或弹簧疲劳时预紧力降低导致的轴承松动。

3 结语

空气涡轮起动机工作过程的振动信号具有时变性,尤其是出现振动异常时,呈现出明显的非平稳特征。本文采用短时傅里叶变换对起动机正常及异常状态下的时频谱和切片谱进行对比分析,找出了导致振动异常的零部件及装配因素。分析结果与试验中可能存在的装配偏差形成了验证,能够为空气涡轮起动机后续试验的异常振动诊断提供一定的理论依据。