基于三次S型速度控制算法的移动机械臂末端振动研究

刘益军,李正强,赖建防,吕伟宏

(1. 广东电网有限责任公司 佛山供电局,广东 佛山 528010;2. 宁波天弘电力器具有限公司,浙江 宁波 315722)

0 引言

近些年来,机器人向着轻型化和高速化的方向发展,自身关节和连杆的柔性因素愈发显著,这也导致在作业过程中容易发生振动变形,严重影响了系统的稳定性。因此很有必要对机器人的振动进行抑制。武广平[1]以重载物料转运机器人的刚柔耦合动力学模型为研究对象,通过五次多项式对其关节进行了轨迹规划,避免了加速度突变,使其运动更加平稳。武奎扬[2]提出了一种叠加正弦-梯形基函数的轨迹规划算法来提高柔性臂杆的抑振效果。

本文以UR10机械臂和移动平台Husky组成的移动机械臂为研究对象,将速度控制这一种抑制机械臂末端振动的手段作为研究出发点,针对现有速度控制的不足,设计了一种三次S型速度控制算法,并基于移动机械臂刚柔耦合动力学模型,以仿真手段探究速度控制算法对移动机械臂末端振动的影响。

1 速度控制算法分析

1.1 梯形速度控制算法

在速度控制算法中,梯形速度控制算法因为具有运算简单、响应速度快并且加速度可以稳定在最大值的优点而被广泛应用,但加速度会在加减速周期的始末发生突变,导致机械臂转动关节在转动过程中产生冲击,进而影响到机械臂末端的工作精度,因此常被用于对精度要求不高的工作场合中,如图1所示。

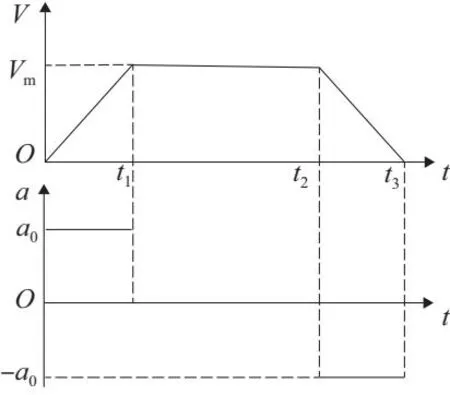
图1 梯形速度控制算法速度曲线

在运动开始时,首先进入加速运动阶段,速度V以常数a0为加速度随着时间t线性增大并在t1时刻达到最大速度Vm,随后进入匀速运动阶段,到t2时刻开始进入减速运动阶段,速度V开始以常数-a0为加速度随着时间t线性减小并在t3时刻降为0。

1.2 S型速度控制算法

S型速度控制算法[3]是以梯形速度控制算法为基础,将加减速运动阶段各细化成3部分,整个速度控制算法曲线由7个部分组成(图2)。其中Vm、am、Jm分别代表着最大速度值、最大加速度值和最大加加速度值。

图2 S型速度控制算法速度曲线

从图2中可以得到速度表达式(1),其中ti表示为各个阶段时刻,Vi表示各个阶段时刻所对应的速度。与梯形速度控制算法相比,S型速度控制算法有效解决了其加速度突变问题,对运动系统的冲击小。

(1)

1.3 三次S型速度控制算法

S型速度控制算法虽然有效解决了加速度突变的问题,但仍存在着加速度不连续的问题,其加加速度存在着突变现象,为此对其加加速度进行优化并提出一种三次S型速度控制算法,将分段恒定阶跃变化的加加速度J改为分段线性函数,通过积分可以得到其速度V的函数,如图3所示。

图3 三次S型速度控制算法速度曲线

根据图3可得到速度表达式为:

(2)

2 移动机械臂刚柔耦合动力学建模

移动机械臂由机械臂和移动平台两部分组成,其中移动平台视为刚体,机械臂考虑柔性关节和柔性连杆两种柔性特征。在对移动机械臂进行刚柔耦合动力学分析时,可以借鉴宏微机械臂的思想对模型进行简化,且将微观机械臂简化成具有固定值的末端质量[4],其刚柔耦合动力学模型如图4所示。

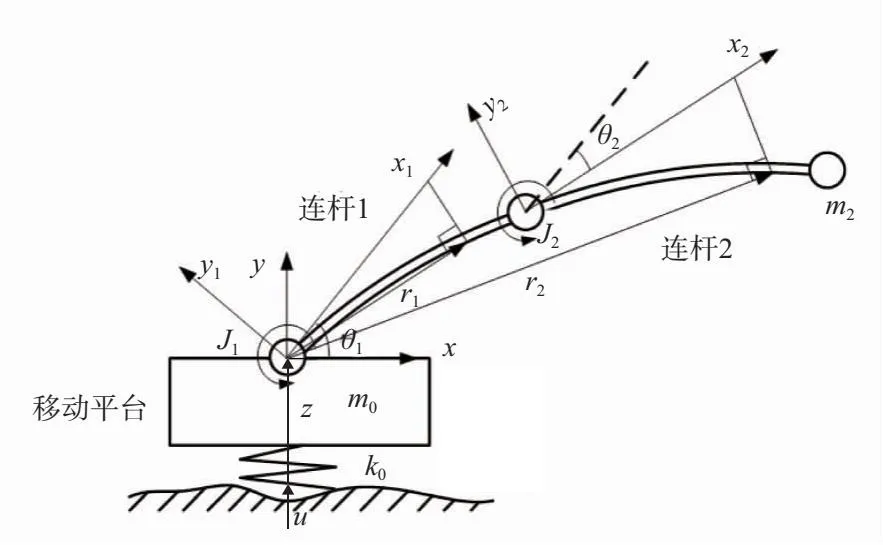
图4 移动机械臂垂向动力学模型

如图4所示,移动机械臂受路面激励u的作用在垂直向上的方向上位移z;移动平台质量为m0,柔性连杆1的末端负载为m1,其中包含连杆1的末端负载与电机2的质量;连杆2的末端负载为m2;k0为车轮与地面相互作用的等效刚度。移动机械臂的连杆密度为ρi(i=1,2),横截面积为Ai(i=1,2),长度为Li(i=1,2),刚度为EI,i(i=1,2)。柔性关节转动角度为αi(i=1,2),柔性连杆刚性部分转动角为θi(i=1,2),柔性关节的传动比为Ni(i=1,2),柔性关节转动惯量为Ji(i=1,2)。

柔性连杆1和柔性连杆2上的任意点在惯性坐标系O-xy下的坐标分别为:

(3)

(4)

移动机械臂系统总动能E的表达式为

(5)

柔性连杆与负载的重力势能U为

U=(m0+m1+m2+ρ1A1L1+ρ2A2L2)gz+m1gL1sinθ1+

(6)

转子-弹簧系统产生的弹性势能Ve为

(7)

柔性连杆的应变能Ts为

(8)

移动机械臂系统的总势能P包括移动平台的势能、连杆与负载的重力势能U、转子-弹簧系统的弹性势能Ve和柔性连杆的应变能Ts,所以其拉格朗日函数L(θ1,θ2,x1,x2)如式(9)所示。

L(θ1,θ2,x1,x2)=E-U-Ve-Ts

(9)

将式(4)—式(8)代入式(9)可得到移动机械臂的动力学方程表达式为

(10)

3 速度控制算法抑振效果仿真分析

刚体模型的建立是验证仿真模型正确性和实现刚柔耦合动力学的基础,因此需要先建立移动机械臂刚体仿真模型。在对刚体仿真模型进行柔性化处理时,理论上需要对其所有零部件进行柔性化处理来确保精确度,但会带来计算量较大、求解时间长的弊端。因此在刚柔耦合动力学建模中会将仿真模型中的主要部件进行柔性化处理,其他零部件仍被视为刚性体,仿真流程如图5所示。

图5 刚柔耦合分析仿真流程图

3.1 移动机械臂刚柔耦合仿真模型的建立

1)柔性关节的建立

在ADAMS中有两种构建柔性关节的方式,因为在建立柔性关节理论模型时将其等效为“转子-弹簧系统”,本文将在ADAMS中通过添加一个凸台连接输入端和输出端的部件,在与输入端的部件间设置旋转副并添加驱动,在与输出端的部件间设置旋转副并添加一个卷曲弹簧,通过卷曲弹簧带动输出端进行转动,其中扭转弹簧的弹性刚度系数为RV减速器的扭转刚度系数,柔性关节2的模型如图6所示。

图6 柔性关节2模型示意图

2)柔性连杆的建立

目前主要有3种方法可以获取机械臂连杆的柔性体[5]。考虑到移动机械臂结构的复杂性和生成柔性体的准确性,所以利用有限元软件完成机械臂连杆的柔性化处理,然后生成机械臂连杆的*. mnf模态中性文件并导入ADAMS中,生成的刚柔耦合模型如图7所示。

图7 移动机械臂刚柔耦合模型

3.2 路面重构及运动平台相关参数的设置

1)三维路面重构

在ADAMS中有相关的路面文件,但这些文件只能用来分析汽车而无法直接使用,因此需要在ADAMS中重构三维路面。本节采用正弦波叠加法来构建仿真所用的三维路面,主要原理是将路面轮廓Gq(n)进行离散后转换为拥有不同频率的正弦波函数。由于ADAMS中三维路面构成原理与上述所求数据不符,因此需要对上述数据进一步处理[6],按照ADAMS默认的路面文件格式进行编写后生成一个*. rdf文件,导入ADAMS中后得到80 m×4 m的C级三维路面功率谱。

2)移动平台接触参数设置

在进行仿真分析时,移动平台与地面间的接触力和摩擦力设置对仿真效果有很大的影响,若接触力设置不合理,会发生模型穿透或弹飞现象;若摩擦力设置不合理,会导致轮胎在地面上发生打滑现象。本文按照轮胎-混凝土地面的接触参数进行设置,轮胎与混凝土地面的接触力参数如表1所示。

表1 轮胎与地面接触的参数

3.3 速度控制算法抑振效果仿真

移动机械臂在进行作业任务时,移动平台和机械臂的运动状态是多变的,本文只研究移动机械臂在仿真中以0.56 m/s的速度匀速行驶在C级路面上且只有宏观机械臂进行运动,并使用上底×下底×高为0.5m×1.0m×0.5m的平面梯形来替代复杂的空间运动轨迹。

在规划路径中使用IF函数建立完整的梯形速度控制算法对移动机械臂的转动关节进行定义,在3.0 s的仿真时间内仿真20 000步,其中1.0～2.2 s为机械臂作业的时间段,2.2～3.0 s为机械臂结束作业后的时间段。仿真模型的关节3在梯形、S型以及三次S型速度控制算法下的运动曲线如图8所示,其运动参数均符合速度控制算法下的运动变化趋势。

图8 3种速度控制算法下的刚体模型运动曲线

在上述速度控制算法的控制下,移动机械臂刚体和刚柔耦合体模型的末端运动变化曲线如图9所示,其中振动位移曲线为黑色阴影区的轮廓线。为更好地探究速度控制算法的抑振效果,因此只针对1.0～3.0 s内使用速度控制算法后的曲线进行分析并将图9中的振动位移数据进行了整理,如表2所示。

表2 移动机械臂末端振动位移数据 单位:mm

图9 刚体模型和刚柔耦合模型的y轴方向位移曲线

从图9和表2可以看出,三次S型速度控制算法的抑振效果均优于梯形和S型速度控制算法。从整体来看,三次S型速度控制算法比梯形、S型速度控制算法平均振动位移值分别减小68.72%、54.63%。其中,在1.0～2.2s内三次S型速度控制算法比梯形、S型速度控制算法平均振动位移值分别减小63.13%、68.79%;在2.2～3.0s内三次S型速度控制算法比梯形、S型速度控制算法平均振动位移值分别减小73.71%、4%。

4 结语

针对所研究的移动机械臂,将机械臂柔性连杆和关节两种柔性特征考虑在内建立其刚柔耦合动力学模型,并利用仿真手段得到移动机械臂末端的振动位移曲线。结果表明,三次S型速度控制算法在抑振效果方面优于梯形、S型速度控制算法,特别在1.0～2.2s机械臂进行作业时的效果最为显著,其平均振动位移值分别减小63.13%、68.79%,验证了三次S型速度控制算法的正确性和抑振效果的有效性,为后续的振动抑制研究和控制系统的设计提供了参考依据。