机车车辆橡胶元件动态建模及其应用

刘林,张涛,,陈清华,凌亮,王开云

(1. 西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2. 国家高速列车技术创新中心,山东 青岛 266300)

0 引言

随着铁道车辆运营里程的增加,新车及新修线路暴露出的运营维护问题愈发显著。作为一种常见的外部激励,轮轨表面磨耗造成的短波不平顺将极大地加剧轮轨间的相互作用与振动[1-3]。在这种恶劣的运行环境下,若转向架上的悬挂元件不能很好地将轮轨间的高频振动与构架和车体隔离,将导致车辆发生高频颤振,最终加剧车辆各结构部件的疲劳破坏并严重威胁其使用寿命[4]。因此,为深入研究悬挂元件在高频激励下的动态特性,亟需建立更符合实际的力学模型。

作为铁道车辆上常见的悬挂连接部件,国内外众多学者对橡胶元件的动态力学特性及建模方法进行了大量研究。早期,Kelvin-Voigt模型常被用于表征橡胶的频率依赖性,但其在高频域会高估橡胶元件的刚度和阻尼[5-6]。BERG[7-8]基于弹塑性叠加原理将橡胶衬套非线性特征中的应力-位移关系进行分解,分别使用弹簧-阻尼单元表征橡胶的黏弹性特征,摩擦单元表征橡胶弹塑性特征,弹簧单元表征弹性特性。SJÖBERG等[9]使用分数导数模型替换Berg模型中的Maxwell模型,该模型能更好地预测橡胶材料动态特性的振幅相关性与频率相关性。吴杰等[10]采用黏弹性分数导数模型建立了单自由度橡胶隔振器模型,分析了其动态特性。SHI等[11]通过最小二乘法拟合实验数据,获取了铁道车辆上橡胶元件的物理参数。WEI等[12]通过实验测得了不同温度下轨下垫层的物理参数,研究了其动态特性对于车辆-轨道系统垂向振动的影响。

本文基于弹塑性理论建立了机车车辆橡胶元件动态仿真模型,分析了谐波激扰的振幅和频率对橡胶力学特性的影响并将该模型与车辆-轨道耦合动力学模型结合,仿真计算了车辆惰行通过曲线时一系橡胶节点力的动态特性。

1 橡胶元件动态建模与求解

1.1 橡胶元件动态建模方法

基于弹塑性理论,本文建立的橡胶元件动态仿真力学模型如图1所示。该模型将橡胶元件总力Fr分解为弹性力Fe、摩擦力Ff和黏滞力Fv3个力叠加:

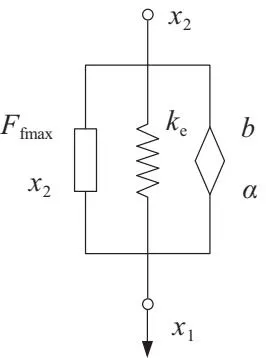
图1 橡胶元件动态仿真力学模型

Fr=Fe+Ff+Fv

(1)

首先引入线性弹簧来表征橡胶元件的静态特性:

Fe=kx

(2)

式中:x=x1-x2为橡胶变形量;k为橡胶材料提供的静态刚度。

其次引入摩擦力来体现激扰幅值对橡胶动态特性的影响:

(3)

式中:u=Ffs/Ffmax;Ffmax为橡胶材料内部提供的最大摩擦力;x2为其达到最大摩擦力一半Ffmax/2时所需的位移;(xs,Ffs)为橡胶元件迟滞回线中每条一分叉线的起始点,初始时(xs,Ffs)= (0,0),之后随振动过程不断更新。

最后引入分数阶微分黏弹性力来体现激扰频率对橡胶元件动态特性的影响:

(4)

式中:b为橡胶材料的阻尼系数;α定义为分数阶微分的阶数,且0 <α<1。

根据Grünwald定义[13],式(4)中的分数阶微分可由式(5)和式(6)进行计算:

(5)

(6)

式中:Δt为积分步长;N为截断阶数,Г(·)为伽马函数。

为充分体现模型的可靠性与真实性,本文采用文献[11] 测得的橡胶元件物理参数进行动态仿真(图1),具体如下:刚度ke为3.998 MN/m,最大摩擦力Ffmax为464 kN,摩擦力位移x2为133 mm,阻尼b为0.516(kN·s)/mm,分数导数的阶数α取0.251。此外,为兼顾计算精度与速度,分数阶微分截断阶数N取200。

1.2 动态响应求解方法

在橡胶元件模型一端引入一质量块后,整个系统即成为一个单自由度的动力学系统。本文采用文献[13] 提出的新型显式积分方法求解其动态响应。该方法的积分格式如式(7)所示。

(7)

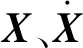
2 橡胶元件动态特性分析

2.1 摩擦力特性

摩擦力的引入可以反映橡胶元件对于外界激励幅值变化的敏感性。由式(3)可知,摩擦力Ff的值取决于x、x2和Ffmax3个量,而x2和Ffmax这两个值为橡胶自身的物理参数,故摩擦力的大小仅与橡胶总的变形量x有关。

为研究1.1节中摩擦力的力学特性,在摩擦力单元一端施加正弦位移激扰x=x0sinωt,绘制不同激扰倍数(分别为x0=2x2和x0=5x2)下的摩擦力-位移特性曲线,如图2所示。可以看出,从平衡位置(xs1,Ffs1)=(0,0)位置出发后,摩擦力及位移会沿正向迅速达到最大值,该处即为分叉点(xs2,Ffs2)。接着向反方向移动,达到负向最大值,此处即为分叉点(xs3,Ffs3)。最后又向正向移动,达到位移为0的位置,此处即为分叉点(xs4,Ffs4)。从第2圈开始,整个循环过程呈稳定且封闭的环状。

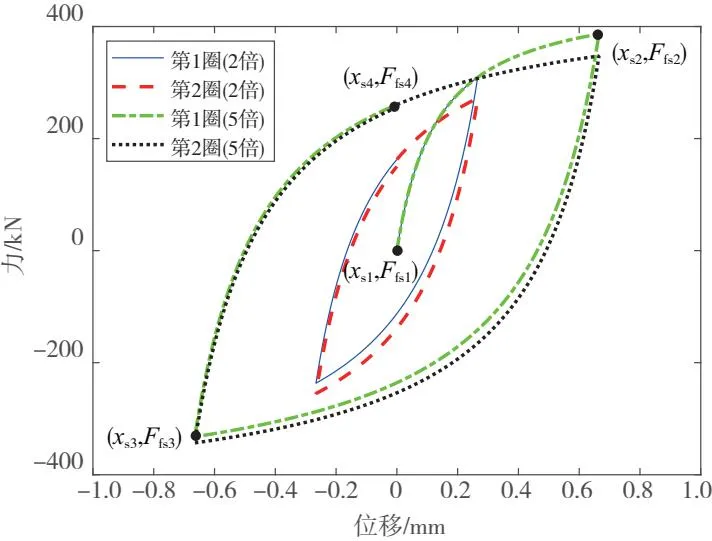
图2 摩擦力-位移曲线

此外,定义等效刚度为力-位移曲线的斜率,即式(8)所示。

(8)

从图2中还能发现, 2倍激扰大于5倍激扰下的等效刚度,这说明橡胶元件中的摩擦力元可以体现橡胶的刚度对于外界激扰幅值的依赖性。

对于谐波激励,准静态力幅值Ff0和每一圈的能量损失Ef可以由以下公式计算[8]:

(9)

(10)

(11)

(12)

式中u0=Ff0/Ffmax。

通过改变幅值x0,可得到不同激扰幅值下的刚度、阻尼特性曲线,如图3所示。可以看出,其刚度随激扰幅值的增大而减小,当x0趋向于0时,刚度值趋向于Ffmax/x2;当x0趋向于无穷时,刚度值趋向于0。此外,图3中的阻尼为一无量纲的量,其值随激扰幅值的增大而增大,当x0趋向于0时,阻尼值趋向于0。

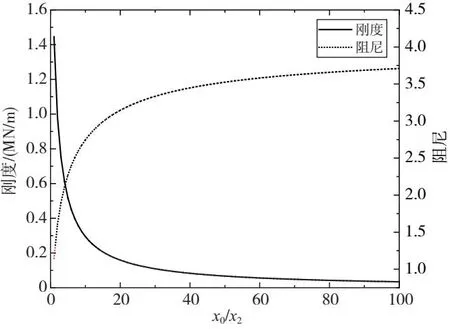
图3 不同激扰幅值下的刚度和阻尼特性曲线

2.2 黏滞力特性

与2.1节类似,为研究黏滞力的动态变化特性,在黏滞力单元一端施加正弦位移激扰x=x0sin(2πft),则不同激扰频率f下的黏滞力-位移曲线如图4所示。

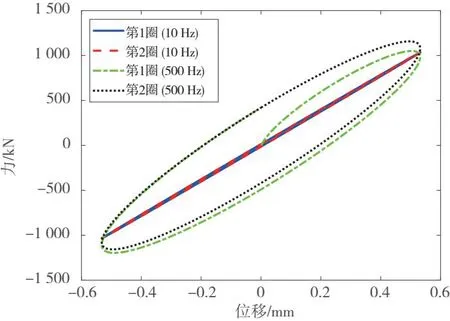
图4 黏滞力-位移曲线

由图4可以发现,黏滞力的动态特性曲线与摩擦力相似,同样在一圈之后会进入稳定状态。此外,当激振频率为500 Hz时,其黏滞力-位移曲线的斜率比10 Hz时更大,说明500 Hz时的动态刚度值更大。其等效刚度同样可由式(8)进行计算,而阻尼的定义如式(12)所示。

(13)

式中E代表每圈循环的能量损失,其值可由黏滞力沿封闭曲线积分进行计算。

由式(8)和式(13)计算出黏滞力等效刚度和阻尼值随外界激励频率变化曲线,如图5所示。可以看出,在0～1 000 Hz范围内,刚度和阻尼值均随频率的增大而增大。这也说明,分数阶微分黏滞力的引入可充分体现橡胶元件对于外界激励频率变化的敏感性。

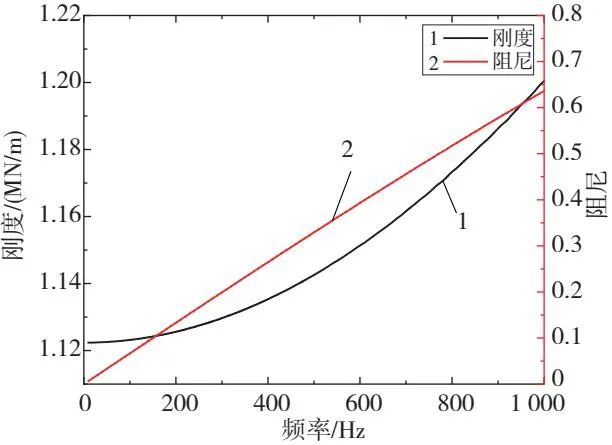
图5 不同激振频率下的刚度和阻尼特性曲线

3 橡胶元件动态模型在车辆-轨道耦合动力学中的应用

3.1 机车-轨道耦合动力学模型

本文采用的机车-轨道耦合动力学模型如图6所示。其中机车模型由1个车体、2个牵引拉杆、2个构架、4个电机和4个轮对构成,各悬挂部件除一系定位橡胶节点(虚线所圈)外均采用普通的弹簧阻尼单元进行模拟。车体、构架和轮对均考虑纵向、横向、垂向、侧滚、点头和摇头6个自由度,牵引拉杆考虑除侧滚自由度外的5个自由度,电机仅考虑其垂向和点头运动。

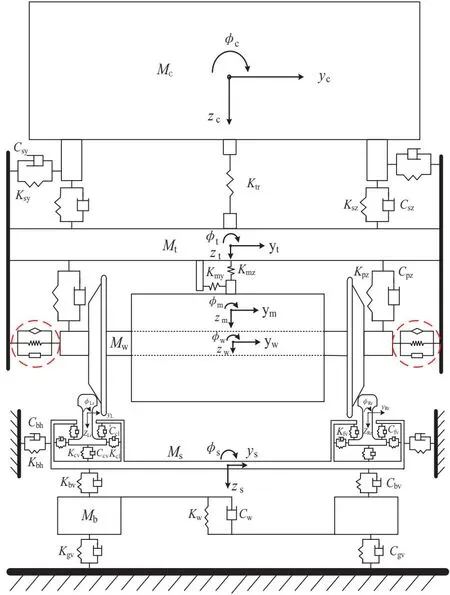
图6 机车-轨道耦合动力学模型

轨道模型考虑了国内铁路常用的有砟轨道,由钢轨、轨枕、扣件、道床和路基组成。其中,钢轨模拟为连续弹性离散点支承基础上的铁木辛柯梁并考虑其垂向、横向和扭转振动。

轮轨接触几何关系采用空间动态耦合模型;轮轨法向力的求解采用Hertz非线性弹性接触理论;轮轨蠕滑力的计算采用Kalker线性理论并结合沈氏理论进行非线性修正[14]。

3.2 曲线通过算例分析

为验证第1节中所建橡胶元件模型在机车-轨道耦合动力学中的实际力学特性,现采用以下曲线通过算例进行仿真分析:车辆运行速度为70 km/h(惰行工况),缓和曲线长度80 m,圆曲线长度为240 m,曲线半径600 m。

图7所示为一系橡胶定位节点处的横向力随时间变化的曲线。可以看出,弹性力、摩擦力和黏滞力的动态变化都经历了稳态—下降—稳态—上升—稳态的过程,这是由于机车运行线路呈直线—缓和曲线—圆曲线—缓和曲线—直线的分布方式。此外,弹性力、摩擦力和黏滞力的大小依次减小,这是由机车车辆上实际橡胶元件的物理特性决定,即提供较大的刚度和相对小的阻尼。

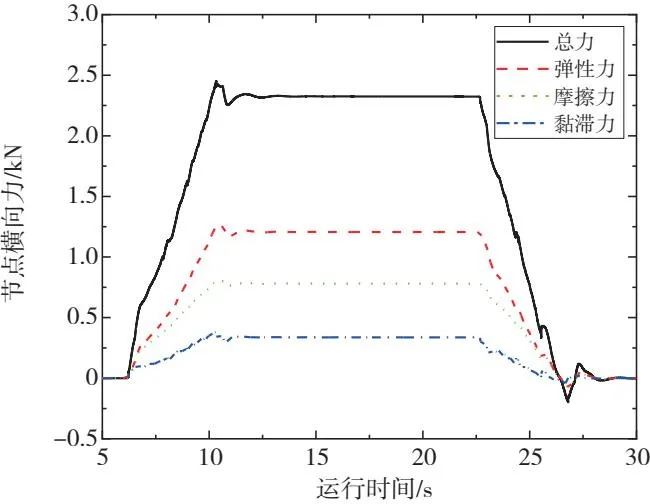
图7 橡胶节点处的横向力响应

图8为橡胶定位节点处的横向力-位移变化曲线。可以发现,对于曲线通过工况,节点总力的动态历程不同于传统的线性弹簧-阻尼单元模型,其中摩擦力表现出一定的非线性特性但并不明显;而黏滞力则呈现明显的迟滞特性。节点总的横向力在弹性力、摩擦力、黏滞力的叠加作用下也呈现一定的非线性特性。

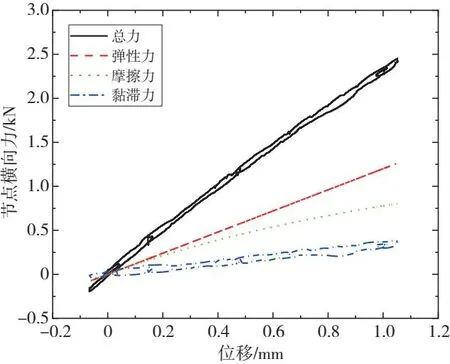
图8 节点横向力-位移曲线

图9(a)—图9(c)为车辆过曲线时,不同阶段节点总的横向力-位移曲线。其中,图9(a)中8 ～ 10 s对应车辆通过缓和曲线,此时节点横向力近似呈线性增长。图9(b)对应于18 ～ 20 s时车辆惰行通过圆曲线,由于车辆运行速度缓慢减小,故此时节点横向力也缓缓减小,且整个动态历程呈螺旋状下降。图9(c)所示为28 ～ 30 s车辆出曲线后的稳态过程。由于此时未受到外界激扰,整个系统逐渐趋于平衡,故该过程中力-位移曲线呈环状向平衡位置(0, 0)处收敛。上述曲线通过算例结果体现了机车车辆橡胶元件的非线性力学特性,也说明本文建立的橡胶元件能够较好地应用于车辆-轨道耦合动力学实时仿真计算。

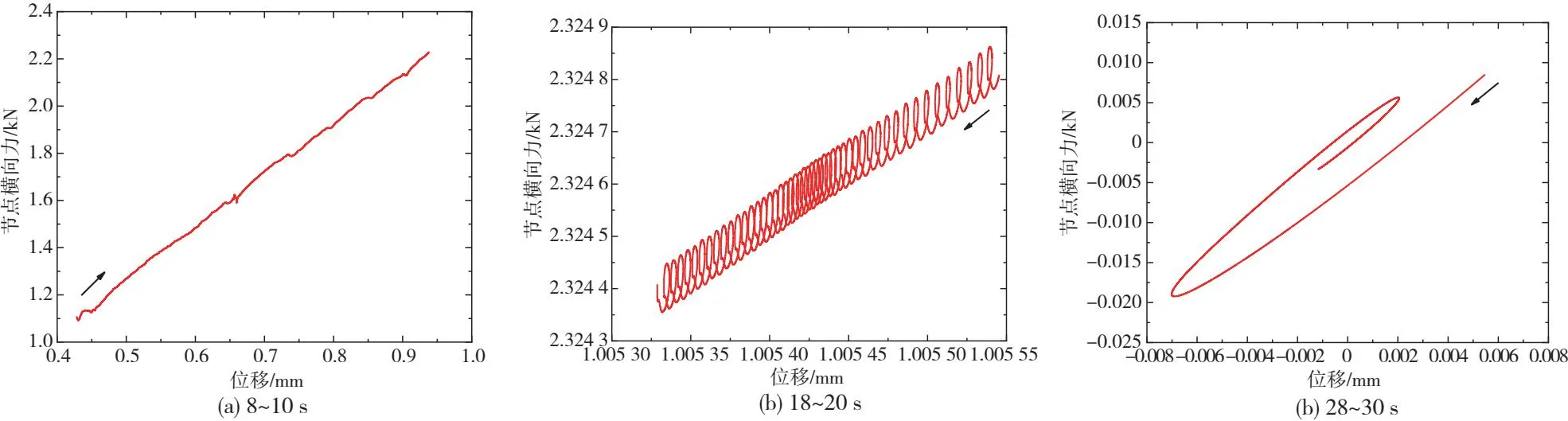
图9 不同阶段节点的横向力-位移曲线

4 结语

本文基于黏塑性理论和橡胶元件的实际物理特性,建立了一种橡胶元件的动态仿真模型,分析了其动态特性并将其应用于车辆-轨道耦合动力学,主要得出以下结论。

1)橡胶元件提供的力可分解为弹性力、摩擦力和黏滞力,其中摩擦力和黏滞力可分别体现橡胶元件对外界激扰振幅和频率的依赖性。

2)橡胶内部摩擦力提供的等效刚度随激扰幅值的增大而减小,阻尼随激扰幅值的增大而增大;黏滞力提供的等效刚度和阻尼均随激扰频率的增大而增大。

3)本文建立的橡胶元件动态仿真模型可较好地应用于车辆-轨道耦合动力学实时仿真计算,且曲线通过算例中稳态—下降—稳态—上升—稳态的过程可反映橡胶元件的非线性动态特性。