一种高频系统信道矩阵低复杂度估计方法

马静艳,李福昌,张忠皓

(中国联合网络通信有限公司研究院,北京 100048)

0 引言

全球5G商用化进程加快,国际各区域和研究组织从2019年开始,已纷纷开启下一代通信技术研究。毫米波/太赫兹通信波段以其丰富的频谱资源,受到学术界和产业界的广泛关注[1],也受到欧、美、日、韩等国家、地区和组织的高度重视,成为极具潜力的6G关键候选技术。毫米波/太赫兹通信可以支持超大工作带宽和超高通信速率,但在实际应用中面临空间传播损耗以及穿透损耗较大的问题和挑战。基于通信覆盖的需求,6G高频通信设备会继续采取超大规模天线阵列方案,用以保证发射和接收增益,实现有效通信,且出于设备性能、功耗和成本的折中考虑,会采用与5G大规模阵列天线技术类似的混合赋形架构实现[2-8]。

4G/5G低频基站一般基于数字波束赋形架构,单数字通道连接单模拟链路,通过参考信号发射和接收完成信道估计[9-10],该类方法无法直接应用于数模混合赋形架构。而已有的混合赋形架构下的信道估计方法多利用上下行信道的互易性来进行算法和方案设计[11-14],实际的上下行信道由于基站侧和用户端的射频收发链路的非理想特性,上下行信道响应会存在性能差异,因此该类方法的信道估计误差及系统波束赋形性能会受到一定影响,且信道估计算法一般都涉及参考信号统计协方差矩阵求逆或特征分解运算[15-18],需要占用较多运算资源,影响信道估计的实时性。

提出一种混合赋形架构设备大规模天线阵列的信道估计方法。该方法可有效估计信道信息,对上下行信道互易性无要求,且通过构造特殊权矢量矩阵,经由矩阵相乘运算来完成信道矩阵估计,避免了统计协方差矩阵求逆或特征分解运算,大幅度降低信道估计算法的计算复杂度和运算量。

1 问题模型

图1为超大规模天线混合赋形架构示意图,基站设备系统链路包括多个数字通道处理单元,每个数字通道对应多个模拟通道,图中,Nd表示系统设备的数字通道个数,Na表示每个数字通道对应的模拟通道个数,Nu表示用户端通道个数。

图1 混合赋形架构示意图Fig.1 Illustration of hybrid beafmorming architecture

定义下行信道矩阵HDL和上行信道矩阵HUL,其中HDL的维数为Nu×NaNd,HUL的维数为NaNd×Nu。为方便公式推导与说明,定义：

(1)

(2)

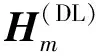
2 算法原理

2.1 下行信道估计

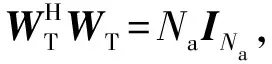
(3)

(4)

发射权矩阵和接收权矩阵可以存储在基站设备赋形装置和用户端赋形装置中,方便调用和切换,其具体构造方法可根据系统硬件架构和性能综合考虑,灵活选择。例如,分别找到Na个波束方向对应的维数为Na×1的等幅波束权矢量,以及Nu个波束方向对应的维数为Nu×1的等幅波束权矢量,使其满足上述加权矩阵的性质,且具有每个元素幅值不变,仅相位有差异的性质。

S=[s1,s2,…,sNd]T,

(5)

则有：

(6)

参考信号sm可使用特殊性质的信号序列来构造,例如ZC序列等,便于在频域映射至各个发射通道,用以通道幅相均衡和校准。

步骤1令基站系统设备各数字通道分别发射对应的参考信号s1,s2,…,sNd,通过在基站侧切换发射权矢量、在用户端切换接收权矢量来获取信道估计使用的数据矩阵,其中基站侧每个模拟赋形模块使用相同的发射权矢量,发射权矢量从wT,m,m=1,2,…,Na中选取,共切换Na次权矢量。

下面分两种情况获取和构造数据矩阵YDL。

情况1如果用户端是数字波束赋形,有Nu个数字通道,则第m次基站侧发射权矢量切换时,用户端设备接收到的数据矢量为：

Xm=HDL(INd⊗wT,m)S+NDL,m,m=1,2,…,Na,

(7)

Ym=XmSH=HDL(INd⊗wT,m)=

[H1wT,m,H2wT,m,…,HNdwT,m]。

(8)

式(8)等效于在每次切换发射权矢量时,将接收端数据进行降维处理,数据维数由Nu×K降为Nu×Nd。一般情形下K≫Nd,因此该处理可以降低存储资源,提高运算速度。

(9)

(10)

式中：vec(·)表示矢量化算子,vec(AM×N)的功能是将维数为M×N的矩阵A按列堆栈,排列成一个维数为MN×1的矢量。

顺序切换Na次发射权矢量wT,m,m=1,2,…,Nd,可得数据矩阵：

(11)

情况2如果用户端是Nu个模拟通道波束赋形,仅有1个数字通道,则当基站侧发射权矢量为wT,m、用户端接收权矢量为wR,n时,用户端设备接收到的数据矢量为：

m=1,2,…,Na,n=1,2,…,Nu,

(12)

式中：nm,n表示下行信道噪声,一般假设为加性高斯白噪声,且与参考信号S不相关。令式(12)左右两边同时乘以SH,将接收数据进行降维处理,数据维数由1×K降为1×Nd,则有：

(13)

根据式(1),式(13)可进一步表示为：

(14)

固定发射权矢量为wT,m时,顺序切换Nu次接收权矢量wR,n,n=1,2,…,Nu,可得数据矩阵：

[H1wT,m,H2wT,m,…,HNdwT,m]HWR。

(15)

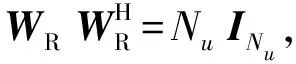
(16)

顺序切换Na次发射权矢量wT,m,m=1,2,…,Na,和Nu次接收权矢量wR,n,n=1,2,…,Nu,可得数据矩阵：

(17)

步骤1的主要功能是通过发射权矢量切换、接收权矢量切换,将接收数据经过降维运算、分块矩阵重新排布等操作构造出可用于下行信道矩阵估计的数据矩阵YDL。针对数字赋形接收端和模拟赋形接收端两种情况的数据构造方法进行了详细说明,其中数字赋形接收端数据构造方法相对简单,且仅需切换发射权矢量,切换次数较少。

步骤2式(3)、式(11)和式(17)等式两边同时乘以WT,可得：

(18)

下行信道估计的详细流程如图2所示。

图2 下行信道估计流程图Fig.2 Downlink channel estimation flowchart

2.2 上行信道估计

与下行信道估计类似,首先分别构建由一组维数为Nu×1的相互正交的权矢量构成的发射权矩阵和由一组维数为Na×1的相互正交的权矢量构成的接收权矩阵。上行信道估计构造的发射权矩阵和接收权矩阵可以重新构造,也可以直接使用下行信道估计时构造的接收权矩阵和发射权矩阵,基站设备赋形装置和用户端赋形装置中只需要存在一组发射权矩阵和接收权矩阵即可。为了在上行信道估计步骤说明时,矩阵定义与下行信道估计不产生混淆,使用WR=[wR,1,wR,2,…,wR,Nu]表示发射权矩阵,使用WT=[wT,1,wT,2,…,wT,Na]表示接收权矩阵。

S=[s1,s2,…,sNu]T,

(19)

则有：

(20)

参考信号sm可使用特殊性质的信号序列来构造,例如ZC序列等,便于在频域映射至各个通道,用以通道幅相均衡和校准。

步骤1令用户端各通道发射上行参考信号s(t),基站侧每个模拟赋形模块使用相同的接收权矢量,接收权矢量从wT,m,m=1,2,…,Na中选取,共切换Na次权矢量。

下面分两种情况获取和构造数据矩阵YUL。

情况1如果用户端是数字波束赋形,有Nu个数字通道。用户端令各数字通道分别发射对应的参考信号s1,s2,…,sNu,用户端无需切换发射权矢量,仅在基站侧切换Na次接收权矢量。接收权矢量从wT,m,m=1,2,…,Na中选取,基站侧每个模拟赋形模块使用相同的接收权矢量,第m次基站侧发射权矢量切换时,用户端设备接收到的数据矢量为：

Xm=(INd⊗wT,m)HHULS+NUL,m,m=1,2,…,Na,

(21)

Ym=XmSH=(INd⊗wT,m)HHUL,m=1,2,…,Na。

(22)

(23)

(24)

基站侧顺序切换Na次接收权矢量wT,m,m=1,2,…,Nd,可得数据矩阵：

(25)

情况2如果用户端是Nu个模拟通道波束赋形,仅有一个数字通道,用户端发射上行参考信号s,可从中任意选取一组,令s=s1。当用户端发射权向矢量为wR,n,基站侧接收权矢量为wT,m时基站侧接收到的数据矢量为：

xm,n=(INd⊗wT,m)HHULwR,ns+nm,n,

m=1,2,…,Na,n=1,2,…,Nu,

(26)

式中：nm,n表示下行信道噪声,一般假设为加性高斯白噪声,且与参考信号s不相关。令式(26)左右两边同时乘以sH,将接收数据进行降维处理,数据维数由Nd×K降为Nd×1,则有：

ym,n=xm,nsH=(INd⊗wT,m)HHULwR,n。

(27)

根据式(2),式(27)可进一步表示为：

(28)

固定接收权矢量为wT,m时,顺序切换Nu次发射权矢量wR,n,n=1,2,…,Nu,可得数据矩阵：

Ym=[ym,1,ym,2,…,ym,Nu]H=

(29)

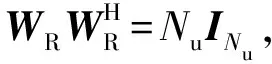
(30)

切换Na次接收权矢量wT,m,m=1,2,…,Na,以及Nu次发射权矢量wR,n,n=1,2,…,Nu,可得数据矩阵：

(31)

步骤1的主要功能是通过发射权矢量切换、接收权矢量切换,将接收数据经过降维运算、分块矩阵重新排布等操作构造出可用于上行信道矩阵估计的数据矩阵YUL。针对数字赋形接收端和模拟赋形接收端两种情况的数据构造方法进行了详细说明,其中数字赋形接收端数据构造方法相对简单,且仅需切换发射权矢量,切换次数较少。

步骤2式(4)、式(25)和式(31)等式两边同时乘以WT,可得：

(32)

上行信道估计的详细流程如图3所示。

图3 上行信道估计流程图Fig.3 Uplink channel estimation flowchart

3 仿真验证

验证所提方法是否能有效估计下行信道矩阵HDL和上行信道矩阵HUL。

仿真条件：考虑一个高频TDD通信系统,基站侧是包含Nd=16个数字通道的数模混合赋形阵列,每个数字通道包含Na=16个模拟通道, 基站侧天线为16×16方阵,每个天线阵元间距为1/4波长;用户端为包含Nu=16个天线的阵列,每个天线阵元间距为1/4波长。

图4 下行信道矩阵估计误差Fig.4 Average NMSE for the downlink channel matrix estimation

图5 上行信道矩阵估计误差Fig.5 Average NMSE for the uplink channel matrix estimation

仿真结果显示,所提算法可以有效实现高频通信混合赋形架构下上下行信道矩阵估计,验证了所提算法的有效性。此外,从用户端为数字赋形架构和模拟赋形架构两种情况下的估计性能对比可以看出,低信噪比条件下,用户端为模拟赋形架构时,性能略优于数字模拟赋形架构。这是由于前者相对于后者,信道估计过程中用户端需要多切换Nu-1倍接收估计权矢量,算法实现方案消耗更多切换时间,可以获取更多与无线信道相关的空间域信息,在低信噪比条件下,对噪声更加不敏感。

4 结束语

毫米波及未来更高频段亚毫米波/太赫兹通信有极大可能继续采用混合赋形架构来实现系统性能和硬件成本及功耗的折中。未来的混合赋形架构中,单个模拟赋形模块包含的通道数可能会越来越多,即Na越来越大,所提方法对运算负担的降低效果也将愈加明显,对未来高频段通信系统的应用实现具有重要意义和价值。