面向航空搜救的无线电数据融合定位方法

白岩康,廉保旺,刘洋洋

(西北工业大学 电子信息学院,陕西 西安 710072)

0 引言

在民用领域,随着海洋事业的不断发展,航行设备更加密集化、多元化、规模化,海上遇险事故日益频繁地发生[1]。海上遇险事故具有很强的突发性,而且遇险的目标一般远离陆地,容易引发人员生命财产的损失,造成严重的社会影响[2]。

在军用领域,多次局部战争印证了可靠的后勤搜救对现代化战争中提高军队作战能力意义重大[3-4]。

近年来,国内外对航空搜救技术的研究主要包括测向定位技术和多源信息融合技术。Alqudsi等人[5]提出的多重信号子空间(Multiple Signal Classification,MUSIC)算法是子空间算法发展中的显著代表,之后Lee等人[6]提出了旋转不变子空间算法(Estimation of Signal Parameters via Rotational Invariant Techniques,ESPRIT)。它利用划分得到的每个单独子阵阵列结构的旋转不变特性来进行信号测向,这一举措避免了MUSIC算法中因存储阵列流形矩阵对硬件系统的高要求,大大减少了测向解算过程中的计算量。2022年,Dong等人[7]提出了 一种适用于宽频带的数字干涉仪测向以及解模糊系统,提供了对应天线阵列的设计方案,并对其中具体的相位解模糊方法进行了详细描述。2019年,Koide等人[8]提出了一种针对相位旋转算法(Phase Rotation Algorithm,PRA)的FPGA高效实现方法,并对其中涉及的硬件架构做了优化。

在多源融合领域,典型的滤波算法有卡尔曼滤波(Kalman Filter,KF)算法、无迹卡尔曼滤波(Unscented Kalman Filter,UKF)、粒子滤波(Particle Filter,PF)等[9]。此外,Shen等人[10]利用因子图模型提出一种可以融合多种输出频率测量信息的多源搜救信息融合方案。该方案使用图模型表示联合概率密度函数,并充分利用了系统的稀疏性,提供了“即插即用”的融合性能,可快速实现各类搜救子系统的添加和删除。在融合故障检测方面,高怡等人[11]提出的状态残差卡方检测法以及对该方法的各种改进是基于分析模型的故障评估检测方法。此外,自回归条件异方差模型 (Autoregressive Conditional Heteroskedasticity Model,GARCH)预测方法以及基于卡尔曼滤波的改进H矩阵方法也都属于可分析模型[12]。为了减少算法的系统开销,参数化置信度传播(Parametric Belief Propagation,PBP)算法得到了广大研究者的关注[13],在PBP算法中,通常使用某种特定的分布对节点消息进行近似,通过最小化KL散度 (Kullback-Leibler Divergence,KLD)计算参数值,只需广播几个参数即可完成节点间消息的传递。另外,随着人工智能的逐渐成熟,无需建立模型而利用特殊的算法使计算机程序对数据进行主动学习,并以此来解决复杂搜救系统融合问题也日渐火热[14]。

综上,无线电干涉仪测向技术比较依赖于对测向体制的深入研究,需要更改相应的硬件资源或者天线的软件算法。而在航空搜救多源信息融合领域,环境噪声条件多基于理想的情况,需要的传感器源数量多,提高了对设备数量、环境和成本的要求[15]。鉴于此,根据目前军民用飞机无线电设备的实际情况,充分考虑机载设备遮挡等实际环境,以无线电测距和测向两种数据作为信息源,通过稳健人工鱼群粒子滤波定位方案对搜救目标进行高精度的测向和定位。结果显示,本文的算法有效提高了复杂环境干扰无线电数据的条件下测向和定位的精度和收敛性,并且具有良好的鲁棒性。

1 系统建模

系统建模主要包括无线电传感器建模和搜救场景建模两部分。无线电传感器部分主要包括无线电测距设备和双天线测向设备。搜救场景部分除了常规的环境噪声以外,飞机上复杂机载装机环境也会对无线电测距测向产生严重的干扰从而导致定位精度迅速下降。

1.1 传感器模型

1.1.1 测距模型

基于无线电的航空搜救系统采用扩频通信体制进行测距,其原理如图1所示。在机载发送端,信源经过扩频和调制,由发射机发射出去,信号经搜救目标接收解调后,延迟固定时间,对发送端进行响应。机载接收端收到搜救目标响应信息后,经数字下变频、相关解扩等处理,测出发射信号和接收信号的时间差,从而计算待搜救目标和搜救飞机之间的距离,系统实现测距的同时也可以实现通信功能。

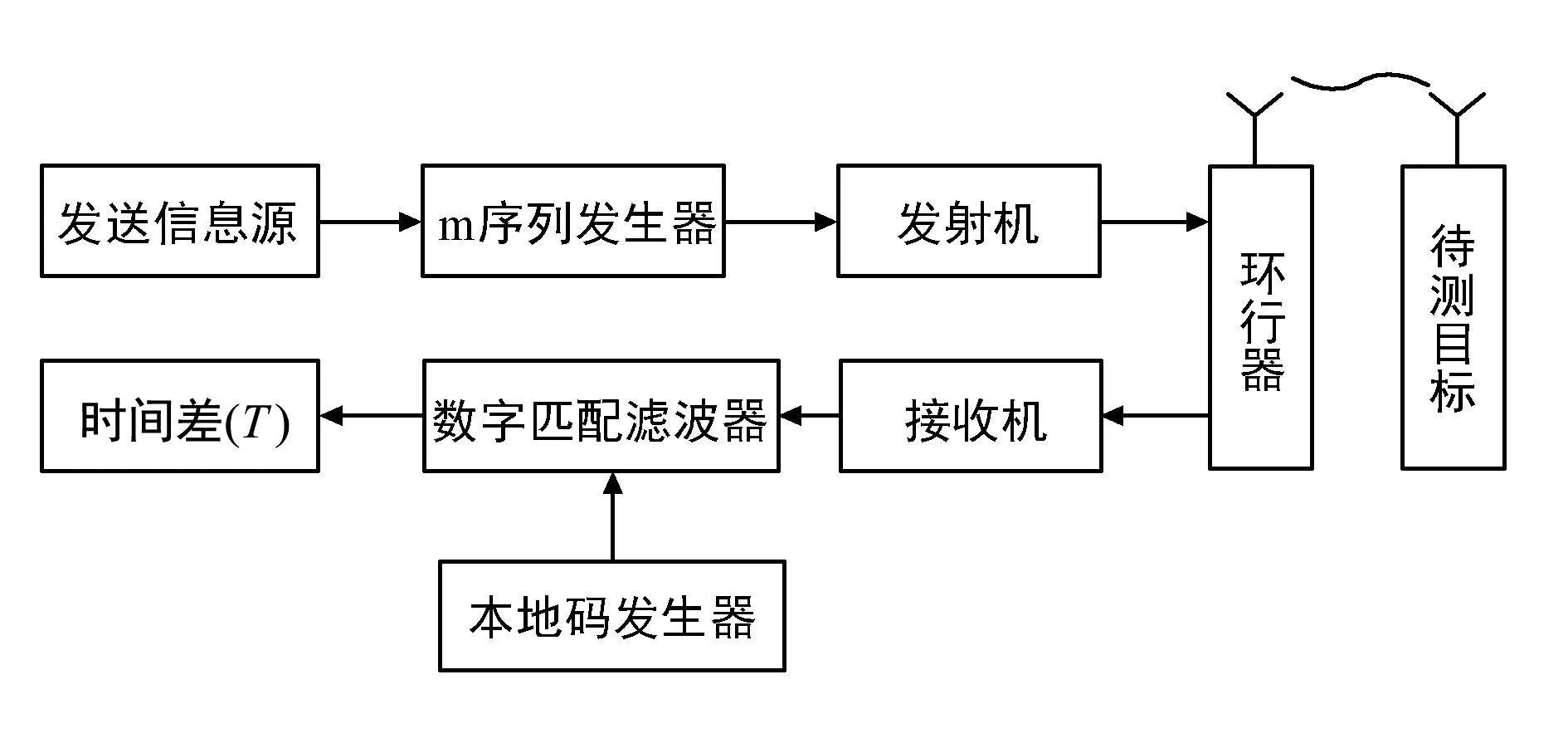
图1 扩频测距系统原理图Fig.1 Schematic diagram of spread spectrum ranging system

测量距离可以表示为：

L=c/2×(T-Δt),

(1)

测距精度为：

P=c/2×(A+Af+Aj),

(2)

式中：T为信号往返时间,Δt为待测目标的响应时间,c为光速,A为扩频码的宽度,Af为发射的时间测算误差,Aj为待测目标的转发时间误差。

1.1.2 测向模型

本系统采用双天线阵列对搜救目标的响应信号进行测向,等间距双阵元的线阵进行信号的接收,测向结构框图如图2所示。

图2 双天线测向结构框图Fig.2 Block diagram of dual antenna direction finding structure

阵列的输出信号可以表示为：

X(t)=AS(t)+N(t),

(3)

式中：A=[A1,A2]T,A1为天线1的导向矢量,A2为天线2的导向矢量;S为搜救信号采样数据矢量,N(t)为2×1维矩阵,代表阵列的噪声数据矢量。

通过阵列列出输出数据协方差矩阵的最大似然估计形式,进行特征值分解,利用下面的函数进行谱峰搜索得到相应的方向角。

(4)

式中：a(θ)为单根天线的方向矩阵的分量。实际无法对协方差矩阵作精确估计,所以用UN表示协方差矩阵的噪声子空间的估计值。对式(4)取倒数即得到双天线多维耦合算法下的空间谱,当该谱取得一个极大值时,说明对应的方向有一个信号入射,该方向即为求救信号的来波方向。

1.2 搜救场景模型

现代航空搜救具有自然环境恶劣、战时强电磁干扰的特点,并且机载装机环境复杂,尤其是安装在飞机底座的测向天线容易受到起落架、轮胎和其他设备的影响而产生遮挡和多径效应。这些特点都会导致搜救信号产生畸变、断续、接收信噪比低,进而引发无线电测向结果发生较大误差,导致搜救目标的定位结果精度低甚至无法定位。

图3为航空搜救场景示意图,搜救飞机装备GPS定位设备、航空搜救设备,遇险人员配备遇险救生终端,通常搜救飞机距离遇险人员约为20～200 km。飞机定位信息由GNSS以及其他定位装置提供,定位误差通常为米级,测距信息主要与时间测量量相关,在复杂机载环境下,测距误差呈现一定分布特性,对定位误差影响较小。测向信息与信号到达双天线的相位差相关,受到设备遮挡、多径等影响,产生较大测向误差,对遇险人员的相对定位引入巨大误差。在现有无线电测距、测向基础上,利用连续多次测量之间的几何相关性,重点关注连续多次测量得到的测距测向信息的滤波、融合处理,从而提升测向精度。

图3 航空搜救场景示意图Fig.3 Description of search and rescue scenarios

2 融合定位方案设计

粒子滤波作为一种可以适用于强非线性系统的滤波方案,没有线性、高斯分布等条件的限制,可以有效克服以扩展卡尔曼滤波为代表的算法精度差、不容易收敛等缺点[16]。粒子滤波本身也有粒子退化和枯竭的问题[17-18],故考虑使用人工鱼群智能寻优算法对重采样等过程进行优化以达到更好的定位结果。

2.1 人工鱼群算法

2.1.1 觅食行为

如果Yj比Yi值更大(默认Y值越大位置越好),那么Xi向Xj方向移动;如果不满足条件,则另选一个随机Yj继续判定。经过try_N次的尝试后,如果都不满足条件,那么随机游走一格,示意图如 图4所示。

图4 觅食行为示意图Fig.4 Schematic diagram of foraging behavior

2.1.2 群聚行为

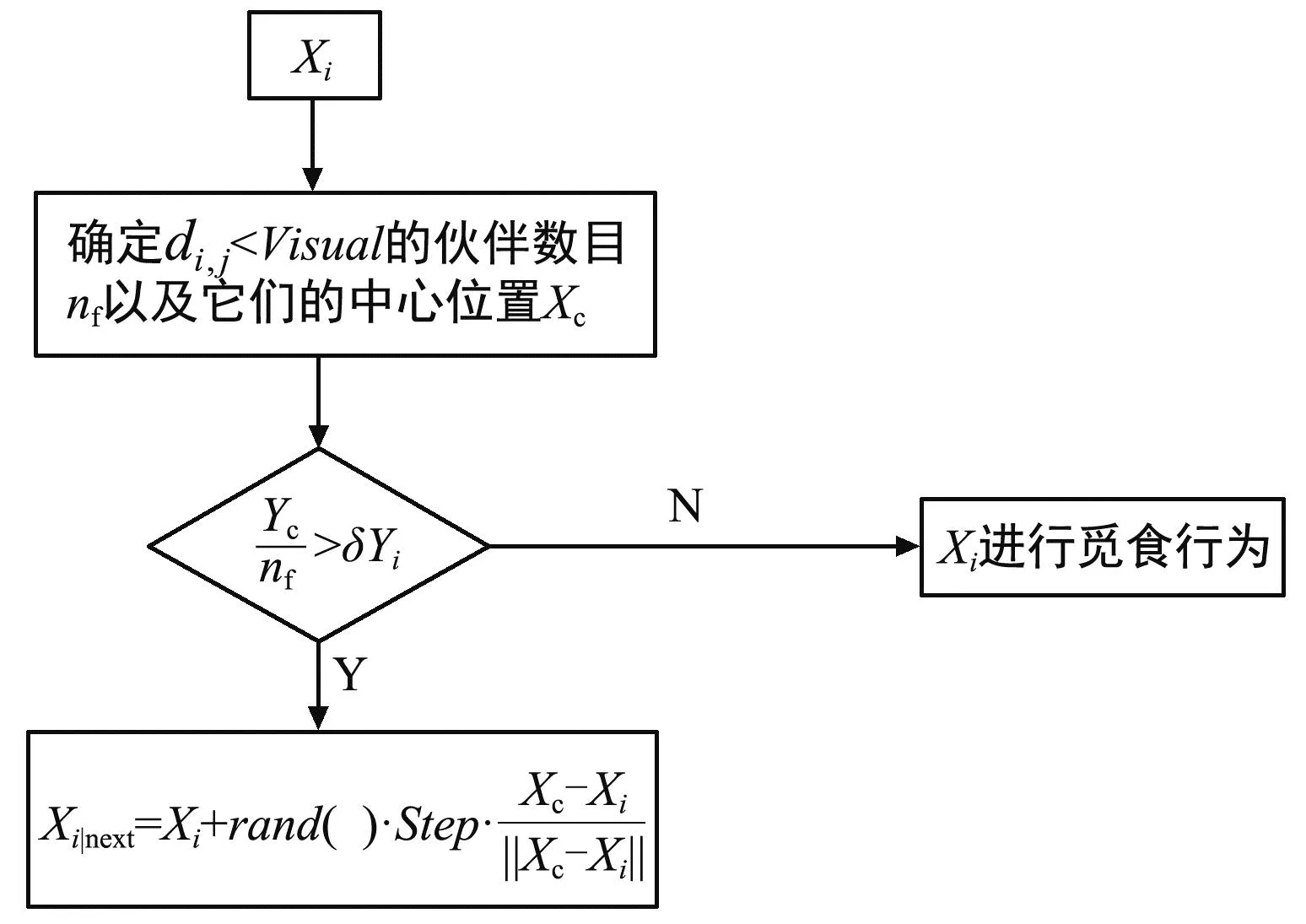
图5 群聚行为示意Fig.5 Schematic diagram of clustering behavior

2.1.3 追尾行为

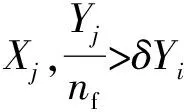
2.1.4 随机游走

当觅食行为不满足条件时,鱼群个体随机向着一个方向游走一步。

2.2 稳健人工鱼群粒子滤波定位

为提高人工鱼群粒子滤波算法无线电航空搜救定位的稳健性,针对人工鱼群做如下三点改进：

① 在觅食行为中,传统的视野选择公式中人工鱼是不能够后退的,为了进一步提高人工鱼的搜索视野范围,将公式修改为：

Xj=Xi+(2×rand()-1)×Visual。

(5)

② 在群聚行为中,需要寻找范围内的同伴然后搜寻局部的人工鱼群体中心位置,导致计算量较大,故考虑选取全局最优中心代替局部中心,而全局最优中心在定位算法中被认为是由如下方程决定的粒子位置：

(6)

式中：dis(i)表示i时刻的测距信息,pos(i)表示i时刻飞机的位置,particle(j)表示第j个测向粒子的坐标。机载设备遮挡对测距的影响要远小于对测向的影响,因此,可利用测距信息辅助修正测向信息。

③ 在随机游走行为中,鱼个体的移动步长很小,影响算法收敛的速度,但是移动步长过大又会导致结果振荡。故而将随机游走时步长策略调整为前期移动快以加快收敛,后期移动慢以提高精度的指数型移动：

Xnext=Xi+ke-λkrand()×Step。

(7)

综合上述改进措施,将改进后的人工鱼群算法融入粒子滤波定位,把鱼群个体看作粒子滤波中的粒子,后验概率密度函数就是目标函数Y,可以得到最终的融合定位方案。

目标后验概率密度(似然函数)为：

(8)

稳健人工鱼群粒子滤波定位方法步骤如下：

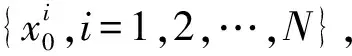
③ 权值更新。根据k时刻最近的测量数据, 每个粒子的权值更新和归一化如下：

(9)

(10)

④ 稳健人工鱼群算法优化的重采样。通过鱼群的4个行为不断更新鱼群个体的位置,每两次迭代功能之间要完成目标函数值和全局最优体的更新。当达到条件要求或者达到最大尝试迭代次数try_N后,鱼群个体的状态和粒子滤波中每个粒子的状态是等价的。

⑤ 定位状态输出。更新人工鱼粒子后,重新计算每个鱼个体的权值并归一化,最后目标位置的最大后验估计如式(11)。若不满足终止条件,则令k=k+1,进行算法的循环。

(11)

3 实验结果和分析

为了证明本文提出的算法能够有效地融合测距、测向和机载GPS信息,达到良好的定位效果和高精度的测向角,本文采用Matlab进行仿真实验。

环境参数设置如下：假设各传感器数据每2 s输出一次,各个传感器之间已经完成了时空对齐,机载航向角和机载GPS位置信息视为准确已知。仿真前已经在陕西省宝鸡市渭河高速等路段进行了实际数据采集,经过分析,测距数据精度和飞机与手持台的距离约成正比关系,设置为满足30～250 m的均匀误差。测向信息受遮挡影响引入较大误差,从3°～20°不等,考虑其最差情况,设置其误差满足均值为20°、标准差为2°的正态分布。

只考虑二维的情况,搜救目标持有手持台在洋流作用下移动十分缓慢,设置为静止不动,位于直角坐标系的原点。搜救飞机的速度设置为100 m/s,仿真时长为600 s,与搜救目标的距离可在25、50、75、100 km中选择,飞机的飞行路径选择为常规曲线,飞机和目标估计位置如图6所示。从图中可以看出,表示目标估计位置的绿色圆形标识在刚开始时和真实位置差距很大,随着飞机的航行,不断采集距离和角度的信息使得估计位置不断向真实位置收敛。

图6 飞机和目标的位置轨迹图Fig.6 Location trajectories of aircraft and targets

图7为目标估计的位置误差,开始的10 s属于算法初始化时刻,不计入统计范围。从图中可以看出,两个坐标轴方向的位置误差从最初的16.8 km,较快地收敛到3 km内,180 s时刻达到300 m内,最终稳定在155 m左右。600 s内的x轴距离误差的均方根误差(Root Mean Square Error,RMSE)为 132.63 m,y轴距离误差的RMSE为214.62 m。

图7 目标估计的位置误差Fig.7 Position error of target estimation

图8为融合后目标角度误差,可以看出,在持续较大的测向数据误差影响下,所提算法可以在1 min内将测向的误差从12.4°收敛到3.0°以下,最终稳定下来。图9为不同搜救距离下所提算法的角度误差对比图,可以看出,该算法搜救距离在50、75、 100 km时,均在1 min左右实现收敛,测向精度随时间继续缓慢提升,在第3 min时,测向误差达到 2.85°、2.10°、1.44°。搜救飞机距离目标25 km时,在 1 min时,测向误差收敛至 8.82°,在第4 min时,进一步收敛至5.91°。从图9可以看出,远距离的测向效果比近距离要好,这是因为搜救飞机距离待救目标越近,相同测距误差对测向误差的影响越大。

图8 目标角度误差Fig.8 Target angle error

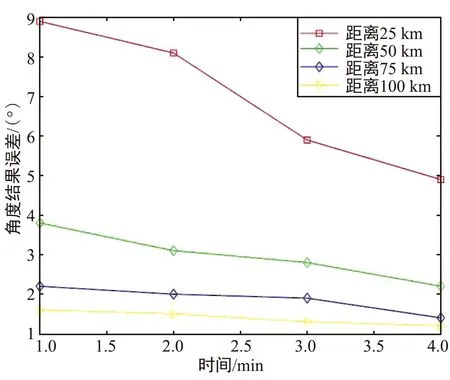
图9 不同距离下角度误差对比Fig.9 Comparison of angle errors at different distances

4 结束语

本文通过对无线电扩频测距信息和双天线测向信息的融合处理技术进行研究,提出了一种基于稳健的人工鱼群粒子滤波算法,通过引入人工鱼群算法优化了传统粒子滤波的重采样过程,模拟人工鱼的觅食、群聚、追尾和随机游走等行为,引导粒子向高似然区域移动,解决了粒子退化和枯竭的问题,并提出了相应的改进方法以提升算法对策准确度和稳健性,进而借助相对准确的扩频测距数据对测向数据进行修正,实现在二维平面上对静止目标的高精度定位。实验结果表明,该算法可以有效融合距离信息、角度信息和机载GPS信息,获得良好的位置和角度估计结果,收敛速度快,具有良好的实时性和鲁棒性。