基于BCJR网格的3×3核极化码简化连续消去译码算法

李逸飞,黄志亮,张莜燕,周水红

(浙江师范大学 物理与电子信息工程学院,浙江 金华 321004)

0 引言

极化码最早由Arikan教授提出,是一种理论上证明在离散无记忆信道中可以达到信道容量的编码方案[1]。2016年,3GPP会议选择了极化码作为5G控制信道增强移动宽带场景的编码方式[2]。Arikan教授提出的极化码的编译码是基于2×2核矩阵构造的,其码长只能为2n。2010年Korada等人[3]指出基于核矩阵构造出的极化码可以拥有更优的纠错性能。

对于任意的ε>0,码长为2n的极化码在连续消去(Successive Cancellation,SC)解码下的误帧率为o(2-2n(β-ε)),β为极化因子,其中2×2核矩阵的β值为0.5。极化因子的定义同时可以推广至任意的大核矩阵,并且可以设计出具有更大极化因子的大核矩阵[3-6]。不同大小的大核矩阵(m×m(m>2)核矩阵)分别对应不同的最优极化速率。一般来讲,更大的核可以有更大的极化速率,在相同码长下,极化速率越大,对应码性能越好。

文献[3]同时指出,大核矩阵在译码中往往会有更高的复杂度,直接的SC译码对于大核矩阵是不实际的。极化码的核内部运算可以借助于网格图来计算,网格是一种有向分层图,最早出现在计算复杂性理论的有限自动机的研究理论中。研究结果表明通过网格可以有效地降低SC译码运算量,节省运算时间[7]。针对大核矩阵带来的复杂度增加的问题,将传统网格与极化码的译码过程结合起来,提出用BCJR(Bahl,Cocke,Jelinek,Raviv construction)网格计算来替代传统SC译码过程中信道转移概率的计算,通过搭建SC译码树来降低算法的计算量。

1 极化码简单回顾

1.1 极化码

图1 极化码模型图Fig.1 Model diagram of polar code

对于任意给定的信道,基于不同的核矩阵设计出对应的极化码都有一组对应的参数(N,K,A,uAc)。N是极化码码长,K是信息位位数,集合A是由K个信息位序号组成的,uAc为冻结位的取值[10-13]。

大核矩阵的译码方式与原G2核矩阵的译码方式大致相同。对于一个给定的m×m核矩阵Gm,针对SC译码,信道转移概率的计算公式为：

(1)

式中：ui∈{0,1},i=1,2,…,m。

以Gm为核矩阵构造的极化码的 SC译码通过直接计算的复杂度为O(2mNlogmN),它随核大小m呈指数增长。本文提出的网格译码就是通过计算网格起点到终点所有路径的流量和来替代式(1),降低计算成本[14-16]。

1.2 最小网格构造

① 网格

网格是一种特殊的图结构。用T=(V,E,∑)表示,其中集合V称为T的状态(顶点集),E称为边(分支),∑为边的符号集。且必须满足以下条件：网格T的状态集合V,由n+1个子集的并集构成,由式(2)表示[17]：

V=V0∪V1∪…∪Vn∪Vn+1。

(2)

在顶点Vi和Vi+1中会有一条边连接,记作ei,同时在边上可能会有一些特殊的标记值,用来进行计算或者存储网格的其他信息,记作α(ei)。

② 最小网格

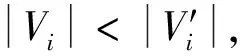
目前,最小网格的构造方法已经十分成熟,常用的构造方法有4种,本文用到的BCJR构造方法就是其中一种,除此之外还有Forney构造方法、Massey构造方法及KS(Kschischang-Sorokine)构造方法[7]。

1.3 BCJR网格构造

设码C是一个在IFq上长度为n的线性码,H=[h1,h2,…,hn]是码C的奇偶校验矩阵,则BCJR网格图T可以通过标记节点Vi集合来构造。

时刻i的顶点集合由式(3)指出：

(3)

V0={φ}={0},

(4)

Vn={φ}={0},

(5)

式中：V0和Vn都是0的集合。

从开始节点V∈Vi-1到下一节点V′∈Vi有一条边e∈Ei当且仅当存在码字(c1,c2,…,cn)∈C满足下式：

c1h1+c2h2+…+ci-1hi-1=v,

(6)

c1h1+c2h2+…+ci-1hi-1+cihi=v′。

(7)

介于Vi-1与Vi的边记作ei,这条边的边标记α(ei)=ci。

式(2)指出了节点的定义,具体的计算过程如下：

(8)

式中：Gi为码C生成矩阵的前i列,Hi为码C奇偶校验矩阵的前i列。通过上式的计算,可以得出各结点的向量组合,然后得出网格构造[16-18]。

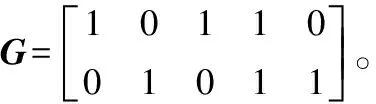
为求出网格,须进行以下几个步骤：

② 根据顶点的计算公式进行各个顶点的计算,其中V0={0},V5={0}。

(9)

③ 根据式(6)和式(7)对网格图进行边标记,根据边标记定义式,绘制出线性码C的网格,如图2所示。

图2 线性码C的网格图Fig.2 Trellis of linear code C

2 基于BCJR网格构造的极化码译码算法

本节介绍通过BCJR网格来进行极化码的译码过程,运用网格结构替代了极化码中的直接运算,根据生成矩阵构造出最小网格,该方法可以有效地降低高维极化码译码复杂度。

作为线性码的核矩阵[5]。

2.1 译码u1

译码u1的过程中只有两个可能性：一种是u1=0的概率;另一种u1=1的概率。

① 译码u1=0的概率

根据式(8),可以求出顶点集合V,根据得出的结点求出其他的列向量组合,具体计算过程如下：

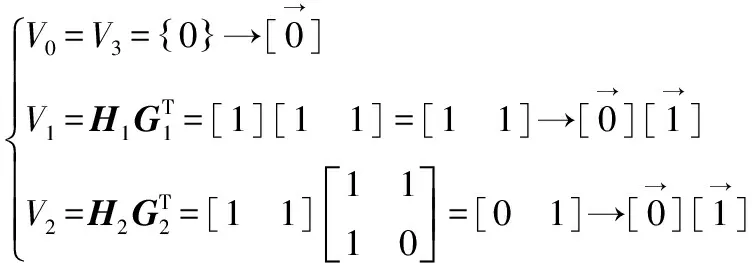
(10)

根据式(6)和式(7),可求解出边标记c,根据边标记可以绘制出译码u1网格,如图3所示。

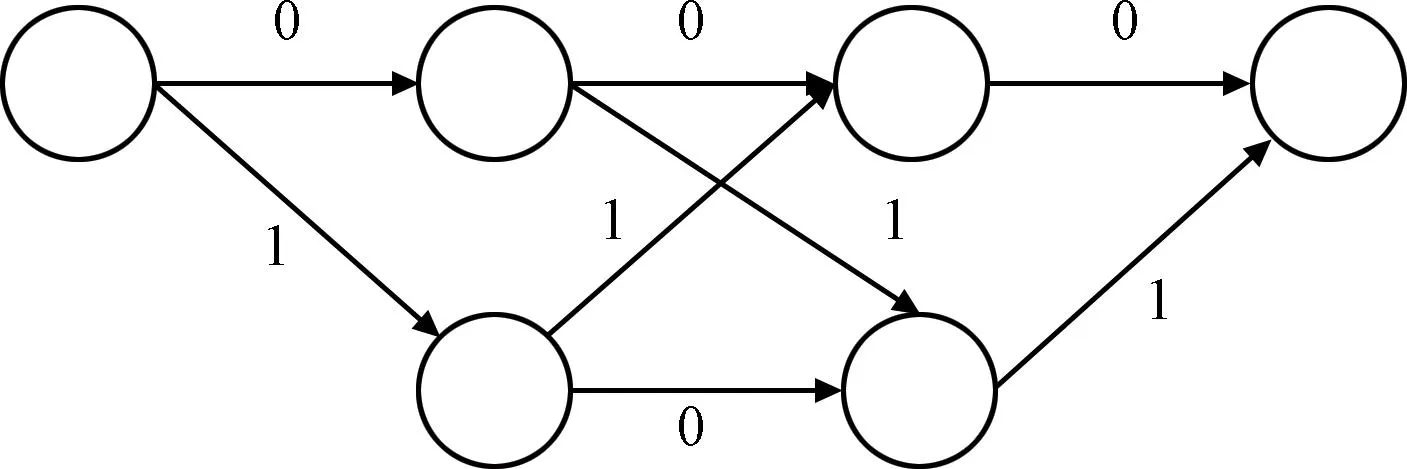
图3 译码u1网格图Fig.3 Decoding u1 trellis

② 译码u1=1的概率

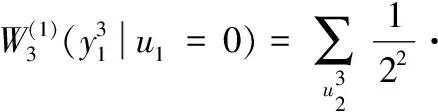
2.2 译码u2

译码u2的过程中,同样u2译码只有两个可能性：一种是u2=0的概率;另一种u2=1的概率。分为两种情况进行,又因为在译码u2时u1已知,需要将情况进行细分。

① 译码u2=0的概率

根据式(8),可以求出顶点集合V,根据得出的结点求出其他的列向量组合,具体计算过程如下：

(11)

根据式(6)和式(7),计算出边标记,绘制出网格,如图4所示。

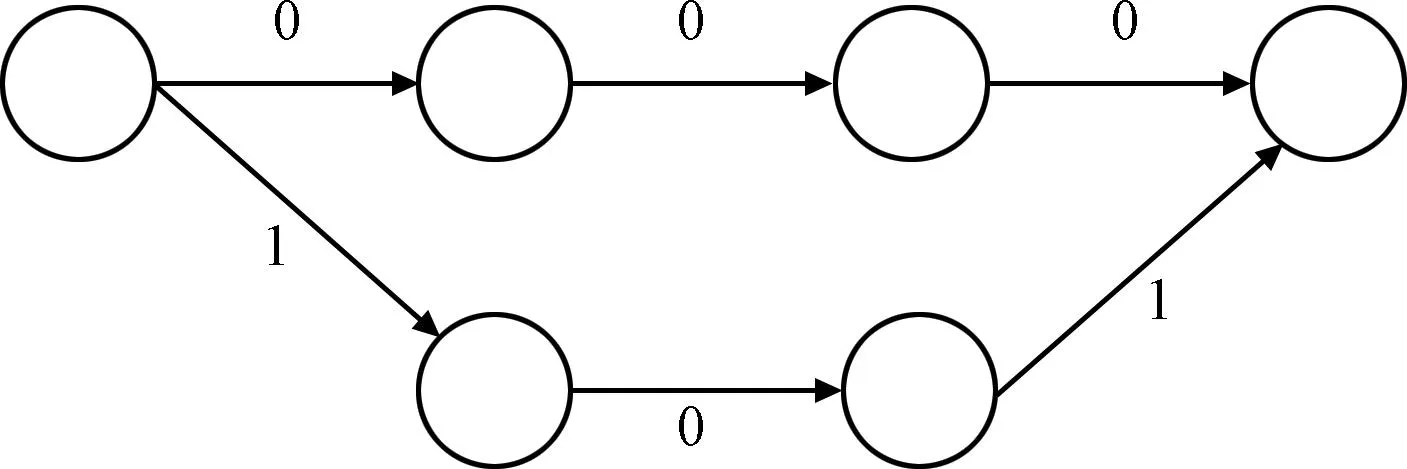
图4 译码u2网格Fig.4 Decoding u2 trellis

② 译码u2=1的概率

2.3 译码u3

上述就是将BCJR网格构造方法应用于极化码译码的大致流程。

3 实验结果与分析

本次实验基于3×3的生成矩阵,设置帧数为1 000 000,在考虑二进制相移键控(BPSK)调制和二进制加性高斯白噪声(BI-AWGN)信道。

具体来说,二进制码字x=(x0,x1,…,xN-1)通过n= 1-2xn映射到传输序列s=(s0,s1,…,sN-1)。在接收端,得到接收向量y=(y0,y1,…,yN-1)。其中yn=sn+zn和z=(z0,z1,…,zN-1)是独立分布的均值为0且方差为N0/2的高斯随机变量集。

实验结果给出了3×3核二进制内核的极化码的误帧率(Frame Error Ratio,FER),设置SNR步进为0.5,INIT_SNR设置为1.0,FINAL_SNR设置为6.0。通过对比传统SC译码的仿真结果,BCJR构造的网格极化码同样有着不错的性能。

表1记录了计算机CPU的性能参数。在实验消耗时间上,设置SNR步进为1,INIT_SNR设置为1.0,FINAL_SNR设置为5.0。统计每轮的计算时间,结果如表2所示。

表1 计算机性能参数

表2 译码消耗时间对比

表3 基于BCJR网格和直接计算式的运算量比较

从图5中可以看出,传统SC译码与BCJR网格译码在SNR相同时FER差异不大。

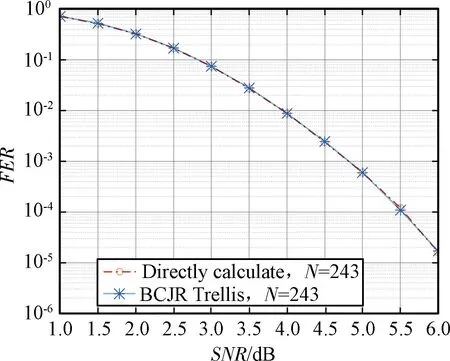
图5 传统SC译码与基于BCJR网格译码的方法 构造的极性码的FERFig.5 FER of polar code constructed by traditional SC decoding and BCJR trellis decoding method

从上述结果可以分析得出,基于BCJR网格的代码运行时间要远远低于传统SC译码所消耗的时间。在算法运行时间上,在相同SNR条件下,综合对比直接计算式运行时间平均减少了79.14%,节省了14.2%的计算成本,有效降低了算法的复杂度。

4 结论

为了解决大核矩阵带来的译码复杂度增加的问题,将传统的BCJR网格与极化码的译码过程相结合,利用网格图的特性,通过计算出起点到终点所有路径的流量和来替代SC译码过程中位信道转移概率的递推计算式,有效地降低计算量。对于3×3核矩阵构造的极化码,仿真结果表明该方法有效降低了算法的运行时间,降低了计算成本。在后续研究过程,将基于此方案将算法推进到更高维的大核矩阵中。