一种基于敏捷集群计算系统的并行GMRES方法
何康馨,席国江,陈 颖
(西南电子技术研究所 敏捷智能计算四川省重点实验室,四川 成都 610065)
0 引言
通信技术和人工智能的飞速发展正在加速促进经济社会向数字化、网络化、智能化转型,在此过程中,通感算一体化已经成为一种新的趋势。为适应这种新趋势,敏捷智能计算四川省重点实验室开发了“雨燕”敏捷智能集群计算系统[1-2]。该系统可灵活部署于飞机、船舶、车辆等载体上,提供接近大型超算中心的并行集群计算能力。基于该系统,提出了一种并行广义最小残差(Generalized Minimal Residual,GMRES)方法来实现大规模线性方程组的快速求解。
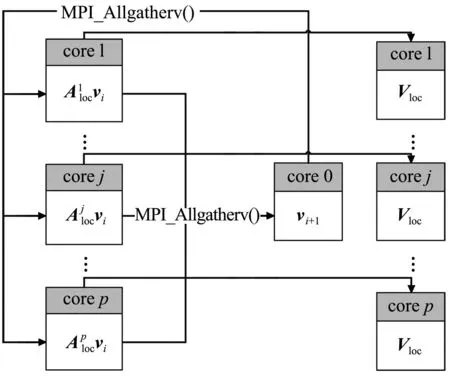
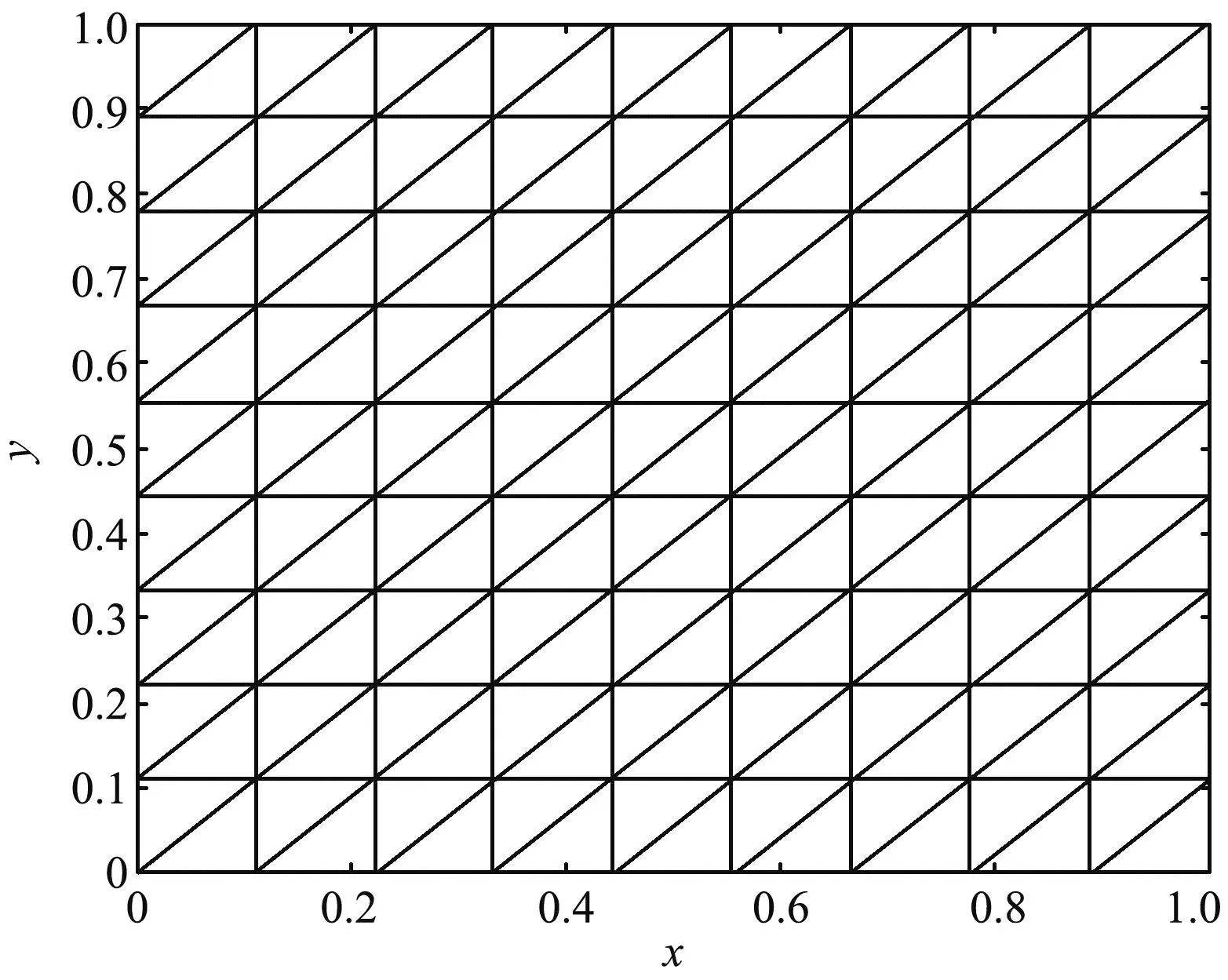
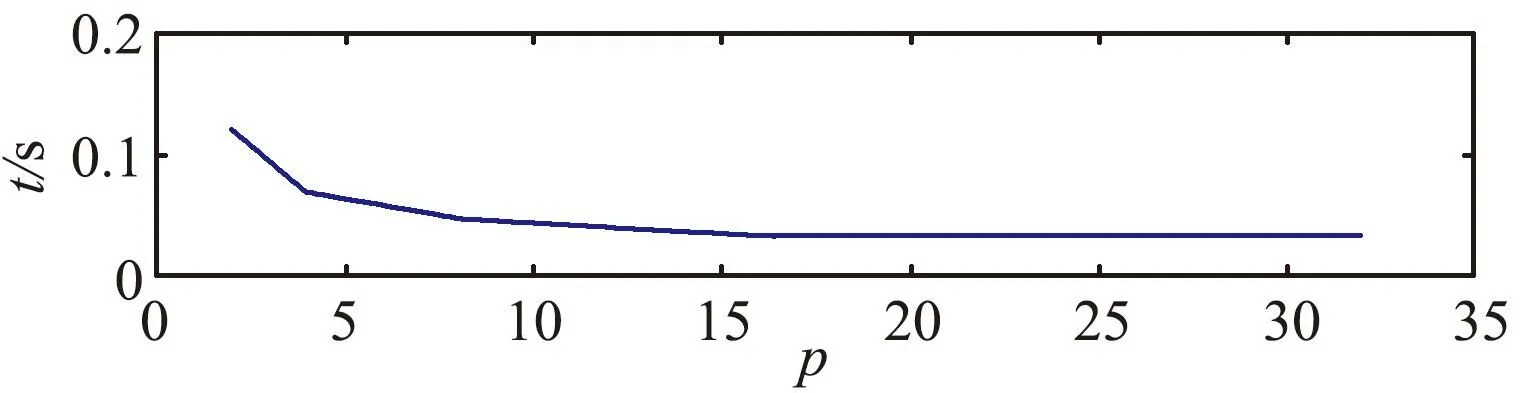
大规模线性方程组的求解是计算数学和工程计算中的核心问题[3-4],也是很多人工智能应用场景的计算基础。在工程实践中,由于存储空间和计算能力的限制,无法采用矩阵分解进行消元计算,因此通常采用迭代法进行求解。常用的迭代方法包括雅可比迭代、高斯-塞德尔迭代、超松弛迭代、共轭梯度法等[5]。在工程应用中最成功的方法是Krylov子空间方法,该方法在n维解空间的m(m 为了充分利用集群计算的优势,出现了大量针对GMRES方法并行实现的工作。Chronopoulos和Kim[8]提出了s-step GMRES方法,该方法通过生成s个同时搜索的方向向量来提高算法的并行性,并在Cray-2分级存储超算上实现。文献[9]探究了一种 预处理GMRES方法在多种并行架构上的实现,包括从分布式和共享内存式的中央处理器(Central Processing Unit,CPU)架构到图形处理器(Graphics Processing Unit,GPU)架构。还有一些工作针对经典GMRES方法进行了并行上的优化,文献[10]通过构造牛顿基来增强GMRES方法的数值稳定性并借助QR分解提高其并行性。文献[11]在分布式架构上,通过通信和计算的覆盖来提高并行效率。 本文基于敏捷集群计算系统提出了一种并行GMRES方法。首先采用矩阵向量乘法构造一组Krylov子空间的非正交基,然后对由这些基为列向量构成的矩阵做并行高瘦矩阵QR(Tall and Skinny QR,TSQR)分解[12],最后由此构造出低维子空间中的一个最小二乘问题并求解,从而得到解在子空间中的最佳逼近。该方法的实现基于多核CPU集群,采用单指令多数据(Single Instruction Multiple Data,SIMD)编程,即同一个程序在不同CPU核针对不同数据执行,数据传递基于消息传递接口(Message Passing Interface,MPI)实现。 本节介绍经典GMRES方法[13]。考虑线性方程组Ax=b,其中A∈Rn×n,x,b∈Rn。Krylov子空间定义如下: K(m;A;r0)=span(r0,Ar0,…,Am-1r0), (1) 式中:m为K的维度,且m≪n;r0=b-Ax0为初始残差。给定方程组解的初值x0∈Rn。GMRES方法寻找近似解x∈x0+K,满足: b-Ax⊥AK。 (2) 该问题与求解如下优化问题等价: (3) 串行GMRES方法主要包括两部分:第一部分是通过Arnoldi过程构建Krylov子空间的一组标准正交基;第二部分是通过求解一个最小二乘问题在子空间中寻找解的最佳逼近。具体过程如算法1所示。 算法1 串行GMRES方法输入:A,b,x0,m输出:xr0=b-Ax0;β=r0;∗Arnoldi过程v1=r0/β;forj=1,2,…,m doq=Avj;for i=1,2,…,j do hij=vTiq; q=q-hijvi;end forhj+1,j=q;vj+1=q/hj+1,j;end for∗最小化 b-Ax,x∈x0+K求解J(y)=miny∈Rmβe1-Hmy得到ymx=x0+Vmym 在Arnoldi过程中构造标准正交基Vm=[v1,v2,…,vm]的过程中有如下关系: (4) (5) 式中:e1=(1,0,…,0)T∈Rm+1。 (6) 在Arnoldi过程中,采用MGS正交化方法来构造Krylov子空间的一组标准正交基。每当生成 一个基向量,就要与前面已经生成的所有向量进行正交化,此过程中存在严重的数据依赖性,影响算法的并行性。进一步地,需要存储的n阶向量v的数量随m线性增长[14],所需计算量随m平方增长[15],在求解大规模问题时会带来巨大灾难。因此,在下节的并行GMRES方法中对Arnoldi过程做出改进。 在并行GMRES方法中,通过两步构造Krylov子空间的一组基,通过并行矩阵向量乘法构造一组非正交基Vm+1=[r0,Ar0,…,Amr0],对Vm+1做TSQR分解来代替Arnoldi过程中的正交化过程。并行GMRES方法的具体流程如算法2所示。算法2的并行过程主要有两部分:一是并行构造Krylov子空间;另一个是并行TSQR分解[16]。 算法2 并行GMRES方法输入:A,b,x0,m输出:xr0=b-Ax0; 并行计算Vm+1=[r0,Ar0,A2r0,…,Amr0];并行计算Vm+1=Qm+1Rm+1;Hm=R(,2:m+1);g=R(,1);求解J(y)=miny∈Rmg-Hmy获得ymx=x0+Vmym 构建Krylov子空间的基向量Vm+1=[r0,Ar0,…,Amr0]需要大量的n阶矩阵向量乘法,会消耗大量的计算和内存资源,该部分的并行效果会直接影响问题的计算效率和可计算规模。Vm+1的并行构造过程如图1所示。 图1 Krylov子空间的并行构造Fig.1 Parallel construction of Krylov subspace (7) (8) 为了降低数据依赖性,将Arnoldi过程中的正交化过程用Vm+1的QR分解来代替。由于m≪n,可以采用并行TSQR算法。Vm+1分布在4个计算核中的并行TSQR方法如图2所示。 图2 并行TSQR方法Fig.2 Procees of TSQR method Rij和Qij的下标i表示计算核的编号,j表示 第j步TSQR分解过程。图2中,Vm+1也按行分布式存储在各个计算核中,在每个计算核中独立地做局部QR分解,例如在第一步TSQR分解过程中,计算核1,得到: V1=Q11R11。 (9) 根据V1的规模和稀疏性,选择Gram-Schmidt正交化过程、Householder变换或Givens变换来实现该QR分解。将得到的上三角矩阵两两结合,并做 第二步QR分解,例如在第二步TSQR过程中,计算核1得到: (10) 重复上述过程,直至得到最终的上三角矩阵Rm+1。 在并行TSQR分解过程中,采用MPI函数MPI_recv()和MPI_send()来实现Rij的数据分发。 本节基于“雨燕”敏捷集群计算平台进行数值实验,该平台包含两颗申威3231 CPU,共64个计算核。测试问题来源于对如下泊松方程的有限元离散[17]: (11) 式中:f=2π2sin(πx)sin(πy)。 式(11)的变分形式为: ∬∇u·∇vdxdy=∬f·vdxdy, (12) 对计算区域Ω进行三角剖分,具体剖分形式如图3所示。 图3 Ω的三角剖分Fig.3 Triangulation of Ω 根据三角剖分,建立有限维子空间Vh= span{φ1,φ2,…,φN},其中φi是分段线性函数,满足: (13) (14) 将积分记作内积,则式(14)变为: KU=F, (15) 式中:Kij=(∇φi,∇φj),Fi=(f,φi)。 图4 误差与Krylov子空间维度m的关系 针对不同规模的K进行数值实验。图5和图6展示了一步并行GMRES方法中,CPU时间t和并行效率E分别与计算核数目p的关系。并行效率E表示单个计算核的平均加速效果,定义如下: (a) n=1 600 (c) n=10 000 (a) n=1 600 (c) n=10 000 (16) 式中:t1表示串行GMRES方法消耗的CPU时间,tp表示采用p个计算核的并行GMRES方法所消耗的CPU时间。 算法消耗的CPU时间包括计算时间和通信时间。随着计算核数目的增加,一方面,每个计算核处理的数据量下降,因此计算时间减少;另一方面,计算核之间的通信量增加,因此通信时间增加。因此图5中的CPU时间随着计算核数目p的增长,减小得越来越慢。当p足够大时,CPU时间甚至可能增加。算法的并行效率与问题规模相关,当问题规模给定时,如图6所示,算法的并行效率会随着计算核数目的增加而下降。 综上所述,应该根据问题规模选择合适的计算核数目。不仅需要考虑消耗的CPU时间,还需要考虑并行效率。因为虽然增大p可以减少CPU时间消耗,但若并行效率过低,则是对计算资源的浪费。因此需要选择合适的p,使得CPU时间消耗较低,同时并行效率较高。据此,当K的规模为n=10 000、 2 500、1 600时,选择的计算核数目分别为16、8、4。 基于该敏捷集群计算平台,并行GMRES方法实现了10万规模线性方程组的快速求解,具体参数及结果如表1所示。 表1 10万规模线性方程组求解参数及结果Tab.1 Computational setting and results of large linear system of order 105 为了能够充分发挥通感算一体化的优势,基于多核敏捷集群计算系统,研究了大规模线性方程组Ax=b的并行解法,提出了并行GMRES方法。并行了串行GMRES方法中计算量最大的部分:一个是构建Krylov子空间过程中矩阵向量乘法的并行;另一个是采用并行TSQR分解代替Arnoldi过程中的MGS正交化过程。通过二维泊松方程的有限元离散,得到不同规模的线性方程组,来验证算法的有效性。 并行GMRES方法本质上减小了数据依赖性,提高了并行效率。因此,在求解大规模线性方程组时,可以充分发挥多核敏捷集群计算系统的计算和存储优势。在未来的工作中,为进一步提升大规模线性方程组的求解效率,一方面可以考虑混合精度算法,另一方面可以开发基于异构计算系统的并行计算方法。1 串行GMRES方法

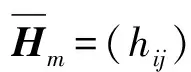
2 并行GMRES方法

2.1 并行构造Krylov子空间



2.2 并行TSQR分解

3 数值实验









4 结束语

