改进扩张状态观测器下永磁同步电动机滑模控制
杨羽萌, 朱其新,2
(1.苏州科技大学 机械工程学院,江苏 苏州 215009;2.苏州市共融机器人技术重点实验室,江苏 苏州 215009)
0 引 言
PMSM因体积小,功率密度大以及转矩控制性能优越等优点,常用于高性能的伺服和调速系统,如航空航天、电动汽车、工业设施等诸多领域[1]。在PMSM控制系统中,经典的比例积分控制技术因其实现简单而仍然受到欢迎[2]。然而,在实际的PMSM系统中,存在大量的干扰和不确定性,这些干扰和不确定性可能来自内部或外部,例如未建模的动力学、参数变化、摩擦力和负载干扰[3]。若仅使用简单的PI控制器,这些扰动以及不确定就很难被迅速抑制[4]。
因此,为了提高具有不同扰动和不确定性系统的控制性能,国内外学者采用了许多非线性控制方法,如SMC[5-6]、自适应控制[7]、模糊控制[8]、自抗扰控制[9-10]、智能控制[11-12]等。在这些现有的非线性控制算法中,SMC算法的特点是当内部的参数发生变化或者在外部有扰动的情况下,SMC依然有较好的鲁棒性,在参数或模型不确定时也保证系统具有良好的跟踪性能。因此,SMC被成功地应用于工业自动化、医疗设备、汽车控制等众多领域[13-14]。文献[15]在传统SMC的基础上,利用开关函数的斜率误差产生显著性效应来确定转子的位置和速度,提出了一种可以在不注入高频信号的情况下精确地观测转子低速(包括静止状态)的角度新的无传感器方案。文献[16]在三相PMSM控制系统中的驱动开路故障中,采用三相四开关容错拓扑驱动,保证故障发生后继续运行。为了提高故障后系统的鲁棒性和动态性能,提出了一种非奇异终端SMC方案。
SMC是一种用于抗扰动的控制方法,它的主要目标是将系统状态引导到一个特定的滑模面上,然后在这个滑模面上保持系统状态稳定。这个滑模面通常是一个确定的超平面,系统状态在这个超平面上具有一定的性质,例如系统状态在滑模面上的漂移速度为零。文献[17]将自适应控制与分数阶SMC相结合,抑制了整数阶SMC的抖振现象,且能实时调整切换增益,提高了系统的控制精度同时提高了进给系统的跟踪性能和抗扰能力。文献[18]将反演控制和SMC相结合设计了鲁棒反演滑模位置伺服控制器,来解决PMSM伺服系统PI控制对转矩干扰和大幅位置波动鲁棒性差等问题。文献[19] 设计了一种新型分数阶滑模转速控制器.通过研究分数阶控制相关理论,与一般的指数趋近率函数相结合,设计了一种新型分数阶趋近率,并将传统的符号函数取代为反正切三角函数。增强电机抗干扰能力和系统稳定性,且鲁棒性更好。
虽然SMC本身就是一种鲁棒性较好的控制方法,但当有外部扰动和系统不确定性时,仍然可能对系统性能造成影响。通过在SMC中引入ESO,可以更准确地估计和抵消外部扰动、模型误差和其他未知动态特性,从而进一步提高系统的鲁棒性。此外,SMC在滑动面上产生高频振荡,可能会导致系统的精度降低。ESO可以减少这些振荡的影响,使得控制器更加平滑,从而提高系统的控制精度。
因此,本文提出了一种基于新型趋近律的SMC,提高收敛速度。同时,利用ESO估计系统状态并抵消外部扰动,且针对传统fal函数易引起系统抖振和误差较大时引起系统增益大的问题,提出了一种新的fal函数,最后在Matlab/Simulink中进行仿真验证。
1 PMSM数学模型
假设电机为线性磁路,则忽略电机的涡流损耗、磁滞损耗、铁芯饱和。转子磁场和定子感应电动势为理想的三相正弦波,PMSM在d-q转坐标系下的电压方程[20]:
(1)
式中:Ud、Uq分别为d、q轴电压;Rs为定子绕阻值;Ld、Lq为d、q轴上的电感量;id、iq分别为d、q轴电流;ωe为电角速度;ψf为永磁体转子磁链。
电磁转矩方程:
Te=3piq[id(Ld-Lq)+ψf]/2
(2)
式中:Te为电磁转矩;p为电机极对数。
使用id=0控制,则有
Te=3pidψf/2
(3)
机械运动方程为
(4)
式中:TL为负载转矩;B为阻尼系数;ωm为电机角速度。
再选取PMSM的状态量:
(5)
式中:ωref为给定转速;ωn为实际转速。
2 控制器设计
对于PMSM控制器的设计,使用一阶微分跟踪器进行跟踪给定信号。SMC系统状态的滑模面,通过控制系统状态在滑动面上滑动,以实现稳定性、轨迹跟踪、抑制抖振等控制目标。同时再利用改进的ESO估计系统状态并抵消外部扰动。
2.1 滑模控制器的设计
传统的趋近律一般选择等速趋近律、指数趋近律以及幂次趋近律。其在SMC中虽然具有一定的优势,但也存在一些缺点和局限性。以下是传统趋近律的一些主要缺点。
1) 抖振问题。传统趋近律在滑模面附近产生高频振荡,这会导致系统产生抖振现象。这种抖振可能会对系统的性能和寿命产生负面影响,并且在某些应用中是不可接受的。
2) 控制信号过大。由于趋近律采用了饱和函数,控制信号在滑模面附近可能会产生较大的幅值,这可能导致执行器饱和或者过度响应,影响系统的稳定性和可靠性。
3) 高频振荡。在实际应用中,由于传统趋近律的高频特性,控制器可能对噪声和传感器误差敏感,这可能导致不稳定或者不精确的控制效果。
因此,为了进一步削弱抖振,本文提出了一种新型趋近律:
(6)

新型趋近律中,使用tanh函数代替符号函数, tanh函数相比于符号函数更为平滑,没有突变,从而tanh函数能有效地削弱抖振。
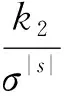
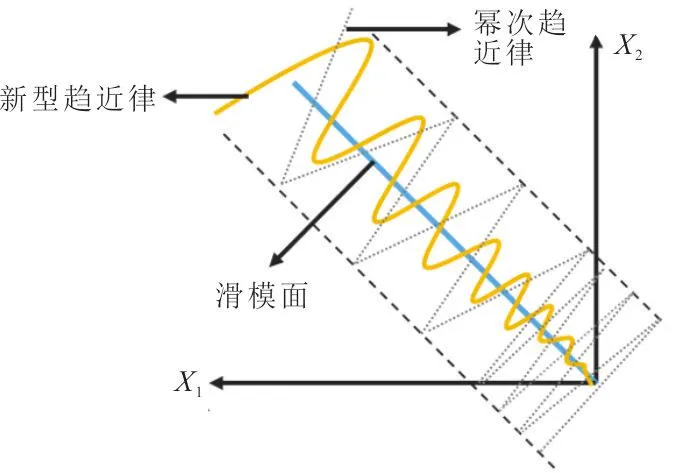
图 1 滑模运动示意图Fig.1 Schematic diagram of the sliding mode motion
(7)
由此可见,该趋近律满足滑模可达性条件,系统稳定。
由式(8)可求得控制律iq:
(8)
2.2 扩张状态观测器(ESO)的设计
ESO是自抗扰控制的核心[23]。标准的自抗扰控制器由跟踪微分器(TD)、ESO和非线性状态误差反馈(NLSEF)3部分构成。
一阶自抗扰控制的原理结构如图2所示。

图2 一阶自抗扰控制原理结构Fig.2 Contural principle structure of first-order self-disturbance rejection
图2中,v为输入,y是输出,Z1为输入信号v的跟踪信号,Z2、Z3为ESO的状态变量,Z2为速度反馈信号的跟踪信号,Z3为总扰动的观测,b是用于外扰和内扰的补偿量,PLANT为被控对象
2.2.1 TD模型
设被控对象为
(9)
则可以将PMSM的机械运动方程改写为
(10)
一阶TD模型为
(11)

在一阶自抗扰控制中,一阶跟踪微分器的作用主要是用于提取输入信号的微分信号以及安排过渡过程[24],但是对于一阶控制系统,对应二阶 ESO 的输出为被控对象和扰动项的观测值,并没有被控对象的微分输出,因此TD只起到滤波的作用。为简化系统结构,提高系统控制的实时性,故省略了 TD 模块。同时使用SMC代替NLSEF。
2.2.2 ESO模型
二阶ESO模型如下:
(12)
式中:β0、β1为ESO的增益。非线性函数fal的表达式为
(13)
式中:δ>0,为常数。
fal函数实质是对“大误差,小增益;小误差,大增益”[25]的函数拟合,虽然非线性fal函数连续,但是在分段点两处,均存在不可导的情况,因此导致在实际情况中,若取值过小,在原点附近容易颤振。为了解决该问题,选择在原点的平滑性相较于指数函数更优的三角正弦函数sin来设计了一个新的连续光滑的非线性hal函数:
(14)
式中:λ为限制量。
为保证|ε|=δ处可导且连续,只需满足函数值与导数相同即可,则有
(15)
其中,hal′为hal的导数。由此可得:
(16)
为验证hal函数和fal函数的性能,取δ=0.2,α=0.245,λ=0.05在Matlab中进行验证,其函数特性曲线如图3所示。
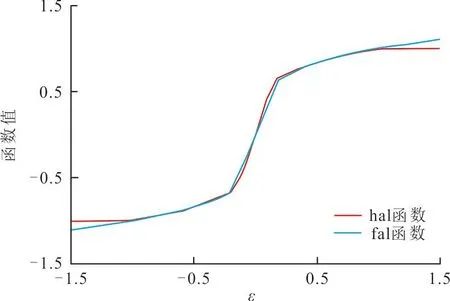
图 3 fal及hal函数特性曲线Fig.3 Characteristic curves of fal and hal functions
从图3可以看出,fal 函数在分段点处有明显的转折,而hal函数在原点周围具有更好的连续性和平滑性。
3 仿真与实验及分析
为验证本文所设计的基于改进ESO的PMSM滑模控制的有效性,在MATLAB/simulink中进行仿真,PMSM所使用到的参数[26]为定子电阻R=2.875 Ω;定子电感Ls=0.008 5 H,极对数p=4;转动惯量J=0.001 kg·m2;永磁体磁链ψf=0.172 Wb;阻尼系数B=0。SMC的参数:k1=k3=10,k2=20,α=0.5,δ=0.2,σ=2.0;ESO 的参数:β0=400,β1=-1。
为验证基于新型趋近律滑模控制器的性能,将其与传统基于指数趋近律的滑模控制器相比较。在PMSM空载启动时,给定初始转速1 000 r/min以确保在实际运行中最大限度地提高能效。0.4 s时,再增加200 r/min的转速,来验证2个控制的跟踪性能。其转速跟踪曲线如图4所示。
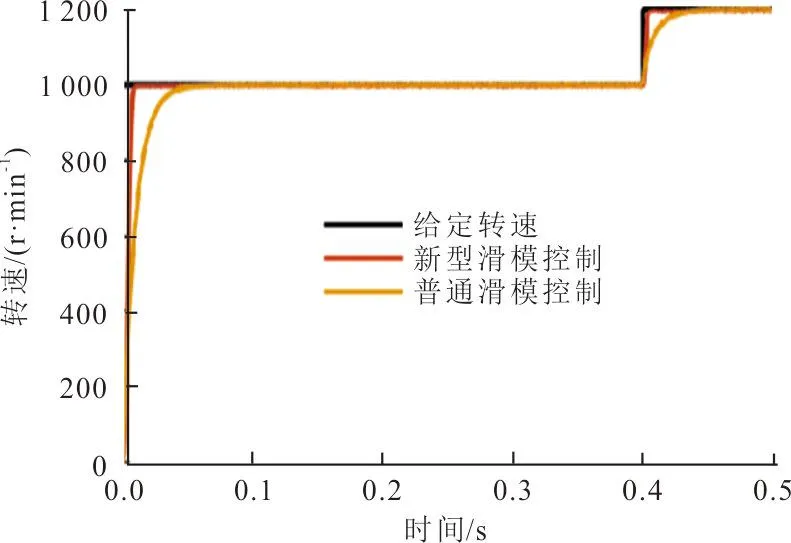
图 4 转速跟踪曲线Fig.4 Speed tracking curve
从图4可以看出,使用2种控制器下的系统均几乎没有超调,但本文所用的控制器有更快的响应时间,为0.017 s,相较传统滑模控制器响应时间0.059 s快0.042 s。0.4 s时加入200 r/min的转速,使用新型滑模控制器的系统在0.407 s跟踪上新加转速且恢复稳态,相较于使用传统指数趋近律的系统在0.445 s跟踪新加转速且恢复稳态的速度上快0.038 s,新的控制器有效地提高了系统的响应时间和跟踪能力。
为验证其抗扰动性能,在0.2 s时,给二者加入同样20 N·m的负载转矩,结果如图5所示。
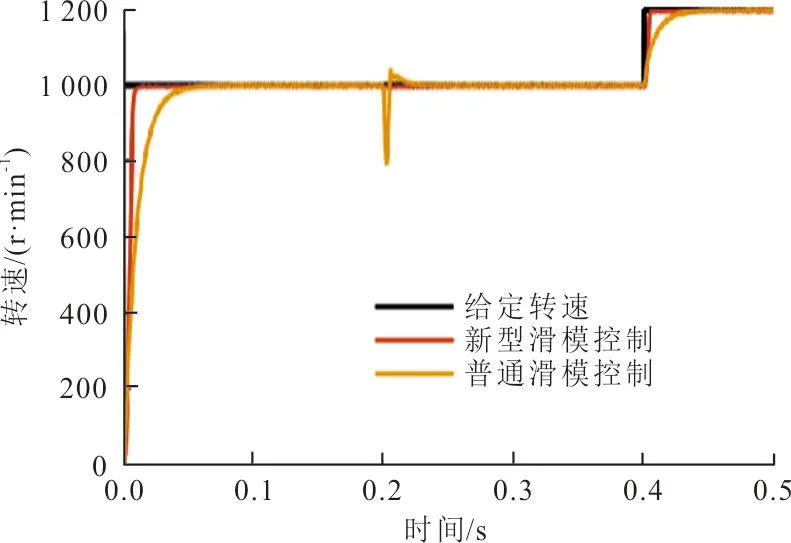
图 5 加入负载转矩Fig.5 The addition of load torque
从图5可以看出,在0.2 s加入负载转矩,用传统的滑模控器控制的系统转速出现了明显的波动,在1 000 r/min中上下波动将近220 r/min,且趋于稳定出现了明显的超调。而用基于新型趋近律的滑模控制器的系统,出现了30 r/min的波动。由此可见,新型滑模控制器有更好的抗扰动性。在转速调节中,能有效抑制超调,并且具有较小的稳态误差,能够柔化控制过程,起到稳定控制的效果。
为了验证本文所提算法抗扰动能力的实际效果,使用图6所示装置搭建PMSM控制系统硬件试验平台进行实验。其电机参数:额定功率750 W,额定速度3 000 r/min,额定转矩2.39 N·m,电机极对数为5对,编码器线数2 500 p/r,转矩系数0.40 N·m/A,系统总惯量2.81×10-4kg·m2实验中,由于平台对最大负载转矩有所限制,在2.5 s时,加入2 N·m的负载转矩,其实验结果如图7、8所示。

图 6 伺服电机机组图Fig.6 Diagram of the servo motor set

图 7 普通滑模加负载扰动Fig.7 Ordinary sliding mode plus load disturbance
从图7、8可以看出,在实物实验中,传统指数滑模控制器控制的系统出现了近200 r/min的波动,而使用新型趋近律的滑模控制仅出现了近20 r/min的波动,很大程度上提高了电机的抗扰动性能。
综上所述,PMSM采用新的趋近律设计的速度环比传统指数趋近律的控制方式具有更好的动态特性。
4 结 语
为较好的提升系统控制性能,本文在PMSM矢量控制的基础上,用基于新型趋近律的滑模控制器代替了传统的PI控制器,在新型趋近律中引入了变速项,使其趋近速度与系统状态相关。并使用ESO估计系统状态并抵消外部扰动,改进了ESO中传统fal函数,优化了函数的平滑性和连续性。通过与传统的滑模控制器做对比,使用所设计的新型滑模控制器的系统,有更好的动态性能和控制精度。本文使用二阶ESO,由于参数较少,二阶ESO的设计和实现相对简单,而三阶ESO的参数更多,设计和实现相对复杂,需要更多的计算资源,但能够提供更高的估计精度。如何将三阶ESO更好应用于系统,需要进一步研究。

