含新能源发电的电动汽车充电站充电功率在线优化策略研究

周卓,芦翔,刘海涛,祁升龙,韩韬,王青

(1.江苏金智科技股份有限公司, 南京 211100; 2.国网宁夏电力有限公司电力科学研究院,银川 750002;3.国网电力科学研究院有限公司, 南京 211103; 4.南昌大学 信息工程学院,南昌 330031)

0 引 言

近年来,为解决能源与环境问题,电动汽车的保有量在各国政府积极推动下迅猛增长[1-4]。然而,因电动汽车充电负荷具有较强的波动性与不确定性,大规模的电动汽车充电将会对传统配电网的稳定运行造成影响,加大电网调度控制的难度[5-6]。随着分布式能源的推广,利用分布式能源为电动汽车充电成为了现代化电动汽车充电站的发展趋势[7-8]：一方面,合理安排停车场内电动汽车充放电能够提高新能源消纳;另一方面,新能源发电系统能够为停车场中的负荷提供功率、降低运营成本[9]。

目前,相关文献已结合新能源发电系统出力的随机性,对电动汽车的充放电行为开展了相关优化研究工作,文献[10]利用前一日的新能源出力以及电动汽车充电负荷数据对电动汽车充电过程进行优化,提高了集合光伏发电的电动汽车停车场充电经济收益;文献[11]提出了两阶段优化策略,降低充电成本、制定停车费用及充电费用;文献[12]利用启发式算法让每个电动汽车自主决策各自的充电策略,然而该方案容易陷于局部最优;文献[13]利用博弈论对各电动汽车个体充电策略进行优化,以降低全部电动汽车用户的整体充电成本。

分析现有文献,结合新能源出力的电动汽车充电功率优化主要目标集中在通过合理规划充放电行为来提高新能源消纳、降低系统运行成本、降低电动汽车充电给配电网带来负荷波动以及为配电网提供备用服务几个方面[14-18]。在含有新能源发电系统的停车场中进行电动汽车充电优化的难点主要体现在：(1)新能源发电出力与电动汽车充电负荷均具有较强的不确定性与时变特性,电动汽车充电方案需根据实际情况实时优化,对优化策略实时性要求较高;(2)每一台电动汽车在充电期内的历史充电功率将对单台电动汽车未来充电计划及充电站运营造成影响;(3)优化过程需要对每一时刻下的电动汽车充电计划进行优化,决策矩阵维度较大[19]。

针对以上问题,文章以含新能源发电的电动汽车充电站为研究对象,考虑新能源发电与电动汽车充电负荷的不确定性,提出一种实时优化策略,旨在降低系统寻优过程计算量、提高优化实时性。

1 优化调度模型

含新能源发电的电动汽车充电站系统结构如图1所示,电动汽车通过充电桩与母线相连,各充电桩均可从光伏发电、小型风力发电以及配电网获得有功功率;控制中心能从充电桩获得当前接入电动汽车信息并控制各充电桩的充电功率、从新能源发电系统控制器获得对未来新能源发电出力的预测、从配电网获得电网状态信息[19]。

图1 含新能源发电的电动汽车充电站系统结构框图

为及时依据系统状态信息对充电站充电计划进行调整,将每24 h设置为96个时段(即每时段时长Δt=15 min),在每时段初始时刻读取充电站各状态信息并依据目标函数对各充电桩未来充电计划进行优化。为方便计算,文中约定每台电动汽车接入充电桩的事件仅发生在Δt=15 min时间段的初始时刻,每台电动汽车与充电桩断开连接的事件仅发生在Δt时间段的结束时刻;在电动汽车连接充电桩后,车主可设置计划停车时长以及离开充电站后下一阶段计划行驶里程(即本次充电期望最低充电量)。

1.1 充电负荷模型

对于任意时段t,充电站中状态变量St可表示为：

(1)

(2)

(3)

配电网为充电站提供的功率：

(4)

1.2 约束条件

(5)

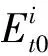
根据功率平衡,由式(4)可以知道站内充电总功率需小于配电网和分布式电源所能提供的实时总功率,即：

PtEV≤PtG+Ptd

(6)

1.3 目标函数

由由(4)可以知道,若电动汽车总充电负荷与站内新能源发电功率变化趋势吻合,电动汽车充电功率完全由新能源发电提供,不再从配电网吸收功率。因此,构建考虑未来24 h内电动汽车充电负荷与新能源发电出力匹配程度的目标函数：

(7)

式中C0为当前时段编号。

当新能源发电功率无法满足电动汽车充电负荷时,充电站从配电网吸收功率,按照分时电价,对该部分功率进行优化,可以进一步降低用户充电成本以及充电站运营成本。因此,构建目标函数：

(8)

式中kt为当前电网电价。

从配电网的角度考虑,电力系统期望充电站负荷平稳,因此构建目标函数：

(9)

综合考虑上述三个优化目标,可以得到文中多目标优化函数：

J(x1,x2…xn)=min(λ1M1+λ2M2+λ3M3)

(10)

式中λ1,λ2,λ3表示三个子目标的权重系数,且满足λ1+λ2+λ3=1;τ=(x1,x2, …,xn)为涵盖未来96个时间段各充电桩计划的决策矩阵。

2 在线优化策略

由前文分析可以知道,针对电动汽车充电过程的优化计算量庞大：以24 h内n个充电桩的优化为例,待优化决策矩阵维度为96×n;同时,任意时刻下充电桩状态(包括是否接入电动车、电动车下一出行计划的目标里程) 的改变均将影响整体的优化结果。因此,文章提出了一种基于状态依赖的决策变量分类方法以降低寻优过程数据计算维度并改善寻优速度。

2.1 基于状态依赖的决策向量分类方法

结合充电桩接入电动汽车的剩余充电时长以及电动汽车未来行驶计划,可以将决策向量分为以下三类：

(1)若充电桩未连接电动汽车或电动汽车已充满,充电桩输出功率恒为0,该类充电桩可归纳为第一组子分量g1,并将该类充电桩从待优化决策变量组中删除;

(2)若充电桩与电动汽车连接,但以蓄电池当前荷电状态在以额定功率充电后仍无法满足(或恰好满足)下一阶段出行计划,充电桩在全时段按照额定功率充电,该类充电桩可归纳为第二组子分量g2,各元素赋值为1并从决策变量中删除;

(3)若充电桩i与电动汽车连接,且不属于以上两种情况,该类充电桩归纳为第三组子分量g3。在充电计划时间内的任意时刻t(t0≤t≤t0+Tti,t0、t、t0+Tti分别记为C0,C和Cn时段),待优化的决策变量xi(C),xi(C+1) ,…,xi(Cn)上界与下界依赖于已完成的充电计划xi(C0),xi(C0+1) ,…,xi(C-1),且依赖关系满足：

(11)

(12)

式中Pave为电动汽车行驶过程中平均耗电量;Lnext为该电动汽车下一出行计划的预期行驶里程。由式(11)和式(12)可以知道,该类充电桩在t时刻待优化变量与已执行的充电计划存在如下依赖关系：

(1)剩余充电计划时间内,总充电能量需确保在充电结束时刻蓄电池储存电量不大于蓄电池总容量(参照式(5));

(2)在充电结束时刻,电动汽车蓄电池储存电能能够满足下一出行计划的耗电需求。

经分类处理后,仅需对g3中决策变量进行优化。容易知道,分类后决策变量维度比原始矩阵小,降低了求解的维度;且在式(11)和式(12)的约束下,第i号充电桩寻优范围将伴随充电计划的进行(剩余充电时长减小)而减小,进一步加快寻优速度、提高寻优精度。

2.2 微分演化算法

传统微分演化算法(Differential Evolution Algorithm,DEA)的优化流程如图2所示。

图2 微分演化算法流程图

经过初始化,得到一系列独立的初始个体如式(13)所示：

(13)

(14)

(15)

随后DEA对新产生的实验种群中各参数种群进行评估选取当前最优参数组合,并与上一种群中各个体进行对比,产生下一实验种群XiG+1如式(16)所示：

(16)

最后,经过多次变异、交叉、选择,当迭代次数达到最大值Gmax,输出当前最优参数组合。

因停车场未来24 h内全体充电桩的充电计划均会对评价结果造成影响且总体充电计划受式(6)约束,直接使用DEA对各时段充电计划优化计算量较大,文中在2.3小节针对该问题设计了基于DEA的求解流程。

2.3 基于DEA的充电功率优化策略

在完成决策向量分类后,仅需对子分量集合g3进行初始化,初始化矩阵g3=(x1,t,x2,t, …,xj,t)T,其中j为g3中充电桩数量。初始化矩阵满足如下规则：

(a)矩阵维度：t时刻决策矩阵g3为j×m阶矩阵,其中NP为种群数量,且m应满足：

(17)

(b)有效元素：因每辆电动汽车剩余充电时长不同,针对第i个电动汽车的决策向量,向量中各元素：

(18)

即第i号充电桩在t时刻的待优化决策向量xi,t,仅需优化t至t+Tti时间范围内的充电变量,其余时刻充电变量均为0。需要指出的是,在初始化阶段,赋值为0的元素不参与后续的优化过程。xi,t中有效元素初始化如下：

(19)

最后,依据式(17)～式(19)构建NP个种群的初始化矩阵,如式(20所示：

(20)

式中G3(i,：)与子分量g3中mod(i,j)号充电桩对应,每台充电桩均有NP个初始充电计划种群。

在得到G3矩阵后,再次依据约束条件筛选出有效决策向量,在有效决策向量集合中针对1～n号充电桩充电计划以式(10)为优化目标,以图2所示的DEA算法对充电桩充电计划组合进行优化,得到当前决策向量集合中的最优决策向量组合g′3。需要注意的是,选取决策向量组合的过程中,只涉及到集合g3中的各充电桩,在评价各决策向量组合的过程中,需同时考虑集合g1与g2所囊括的充电桩。

在得到当前决策向量种群中最优组合后,再次利用式(13)～式(15)对G3中决策向量种群进行变异、交叉,得到一组新的决策向量种群,重复决策向量组合选择流程与决策向量变异流程,直至达到文中规定的迭代次数,完成各充电桩的决策向量优化,并输出完整的最优解。基于上述分组和DEA优化策略,文中构建完整优化解流程如表1所示。

表1 基于DEA的完整优化流程

3 算例分析

3.1 算例参数及场景设定

风力发电系统与光伏系统输出功率由光照强度、温度等当地气候条件决定,现已有大量文献进行了预测研究且达到了较高的预测精度,因此,文章认为充电站新能源最大出力曲线为已知数据。选取一周时长(从周一0：00-周日24：00,共计24×4×7=672个时段)国内某地实测新能源出力数据作为分析依据如图3(a)所示。以文献[20]中统计的用户出行习惯并选取一周时长数据作为电动汽车数据参考,得出电动汽各时段行为概率如图3(b)所示。为简化行驶轨迹,文章将电动汽车行为归纳为：行驶中、在居住区停车场、在商业区停车场以及在工作地点停车场四种情况;相应地,考察一周时长内各时段行驶中电动汽车行驶里程概率如图3(c)所示。

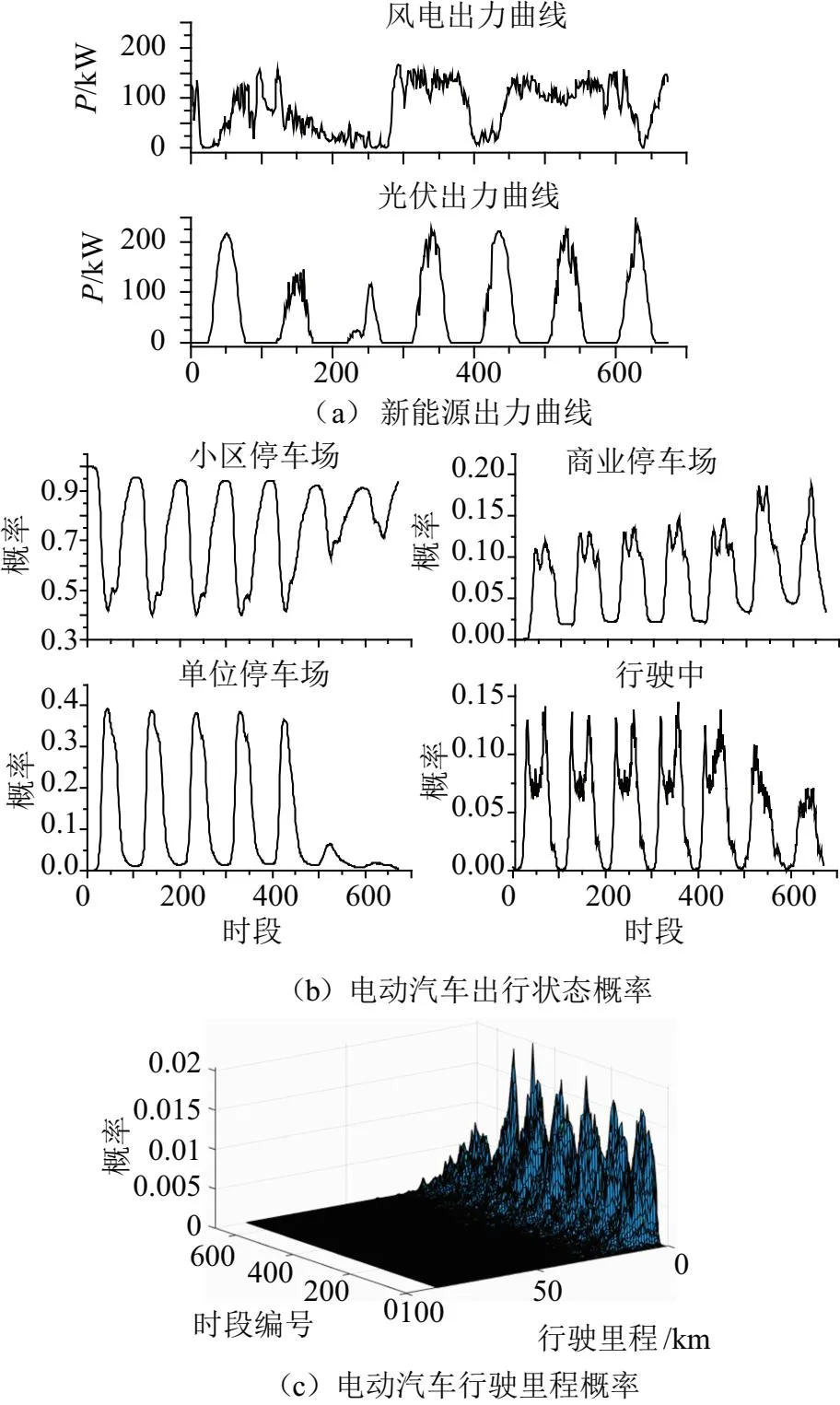
图3 一周内新能源发电数据及电动汽车行为概率

本算例将应用场景设置为城区中基本结构如图1所示的商用公共充电站,按照按图3(b)中商业停车场停留概率设置充电站固定服务电动汽车的驶入、驶离行为、按式(21)设置阶梯电价且每个充电桩未来充电状态为未知,充电桩在每个时间段初始时刻读取充电状态信息(包括剩余充电时间、电动汽车当前荷电状态等信息),并对充电计划进行优化。设定充电站内充电桩共60台、额定充电功率为30 kW,充电站服务附近区域300辆电动汽车(按照停留概率开展充电服务,其余空闲充电桩按随机时间设置连接状态与充电需求),电动汽车电池总容量为60 kW·h,行驶期间耗电量为16 kWh/100 km。

(21)

3.2 优化结果

本算例在CPU型号为i7-6700(3.4 GHz),内存为8.00 GB的电脑上利用MATLAB2016b进行求解;对多目标函数中三个子目标的权重系数λ1,λ2,λ3分别设置为：0.3,0.3,0.4;图2中微分演化算法参数初始化设置：NP=10,F=0.5,CR=0.8,Gmax=80。将文中所提的优化策略与两种无序充电状态进行对比(无序充电1为用户即停即充直至电动汽车电池容量充满;无序充电2为用户即停即充且每次充电目标均为本次充电最低期望充电量)。

依据文中建立的多目标评价函数,考察一周内充电过程,可以得到如图4所示的多目标评价结果。可以看出,采用所提出的优化策略后,一周内多目标评价指标有明显降低。需要指出的是,在本周第一个时段前的充电策略未经优化,电动汽车荷电状态按照正态分布函数随机给出(概率分布函数参见文献[21]),初始时刻多目标评价指标较高。随着优化的进行,评价指标降低。此外,因文中采用的充电策略是对未来24 h的整体充电计划进行优化,无法保证每一时段下评价指标均低于其他两种充电状态下的评价指标,但由图4中结果可以看出,绝大多数时间段下评价指标相较于其他两种充电状态均有明显改善。

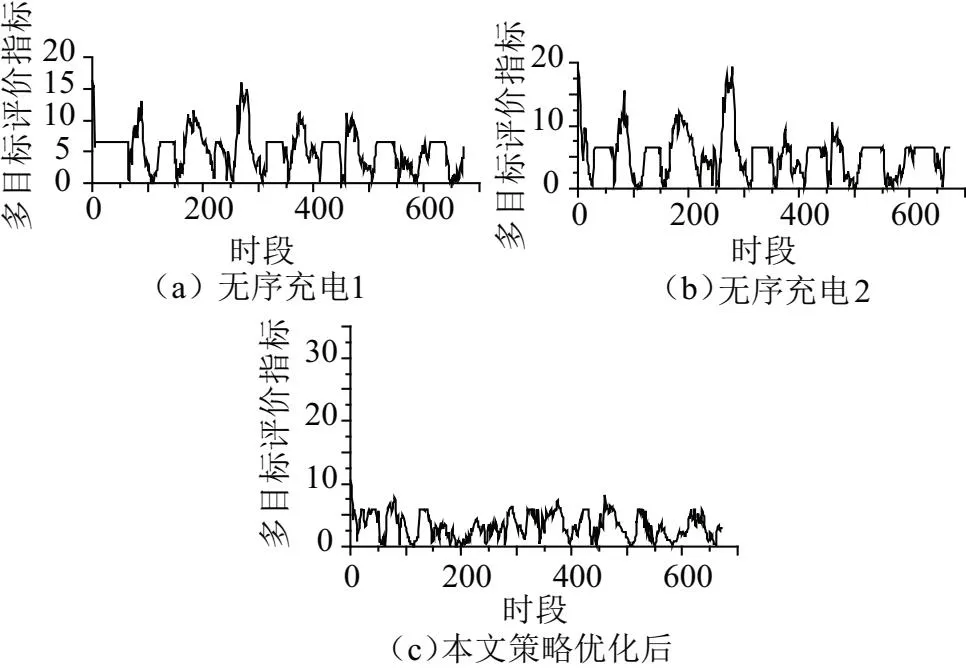
图4 不同充电策略多目标评价结果

依据式(7)对三种充电策略下评价目标1进行对比,结果如图5所示。一周时间内,无序充电1与无序充电2相对于新能源出力差值平方的平均值分别为1.53×105kW与1.58×105kW,采用文中方案优化后,下降为6.50×104kW,电动汽车充电负荷分布更贴近于新能源最大出力变化趋势。

图5 充电功率与新能源发电对比

进一步,三种充电方式下由电网提供的充电功率以及充电成本对比如图6所示。从图6(a)可以看出,采用文中提出的优化策略,停车场由电网提供功率大部分时间段比两种无序充电方式低,且因充电造成的负荷波动最小。但在其他两种充电状态下,因电动汽车蓄电池以最快速度达到目标荷电状态,在部分时间段两种无序充电状态由电网提供的支撑功率小于由文中优化后的电网支撑功率,此类时间段数目相对较少。换算成充电成本的对比如图6(b)所示,综合考虑一周的总充电成本费用,无序充电1、无序充电2以及优化后三种充电方式下,总费用分别为2.48万元、2.46万元以及1.90万元。综上对比可以看出,采用文中提出的控制策略,能够有效地使电动汽车充电功率与新能源发电功率契合、降低停车场充电电费并降低停车场为配电网带来的负荷波动。

图6 一周内由电网提供支撑功率及充电成本对比

按照文中设置,在每时段初始瞬间读取各充电桩状态并开始优化全部充电桩充电方案,在文中所提基于时间基于状态依赖分析的决策变量初始化与分类方法下,各时段g3中元素数如图7所示。

图7 各时段待优化向量数

由图7可以看出,文中所提优化策略能够有效地降低每次待优化矩阵维度,降低决策过程的计算量。相应地,在一周内优化过程单次最大耗时为25 s占充电时长3%以内,满足快速性需求。与传统优化方法相比,一周内平均单次优化时长由26.2 s下降至18.7 s,提高了优化的快速性与实时性。

4 结束语

针对电动汽车充电站充电功率在线优化问题,文中提出了一种改进的充电功率在线优化策略,对各充电桩未来充电计划进行实时优化、确定各充电桩在各时段充电功率。为降低决策过程的计算量,在开展充电方案优化前,通过对决策变量进行分类,降低了待优化矩阵维度;为保证求解的准确性,在寻优过程中两次调用微分演化算法分别对决策矩阵中有效决策向量组合、决策向量进行优化。通过算例分析,可以得到如下结论：

(1)优化结果显示通过文中提出的优化策略能够有效提高停车场新能源发电消纳能力、降低充电站运行成本、降低充电站负荷波动;

(2)文中提出的优化策略具有较强的快速性与准确性,应用在充电站充电功率在线优化中能够有效修正新能源出力、充电站中电动汽车充电行为的随机性对充电计划评价结果的影响;

(3)考虑到真实场景中充电站面临的实际情况远比文中设置的算例复杂,诸如实际充电站规模、极端恶劣天气、充电站其他基础设施负荷、充电站其他运营成本(包含人工成本、场地成本等)等因素均会对优化结果产生影响,文中构建的优化目标函数与限制条件、设置的优化频率以及算例中得出的优化时长仅作为真实充电站运营过程中充电功率在线优化的参考,但文中设计的优化过程与提出的优化策略仍适用于实际的充电站充电功率在线优化。