基于能量系数的电力变压器热故障严重性评估方法

范慧芳,咸日常,刘兴华,张冰倩,陈蕾,高鸿鹏

(1.山东理工大学 电气与电子工程学院, 山东 淄博 255000;2.国网山东省电力公司淄博供电公司, 山东 淄博 255000)

0 引 言

电力变压器在正常运行过程中,内部绝缘材料易受电、热和机械等多因素的作用而会出现老化、放电等现象,若不及时制止,最终会使绝缘击穿,从而发生更为严重的故障,造成设备损坏并引发停电事故[1-2]。因此及时预测变压器的内部潜伏性故障及故障严重程度对整个电力系统的稳定运行意义重大[3]。

现有的溶解气体分析技术(Dissolved Gas Analysis,DGA)大多致力于确定故障类型,但鲜有文章讨论这些故障相应的严重程度。文献[4]虽已从热力学的角度考虑变压器故障的严重性,提出了一种归一化能量强度(NEI)的方法,但最终是对故障严重性进行整体评分,并没有对故障的整个过程合理划分。文献[5]提出能量加权DGA的方法,并基于IEC规范、IEEE标准C57. 104- 2008中规定的变压器状态码和热力学理论,建立模糊推理系统,从而实现了对故障严重程度的判断。文献[6]引入热焓理论分析了变压器内油热解原理,并提出基于能量加权的变压器油中溶解气体总含量的分析方法,该方法提高了热故障诊断的灵敏度与准确率。另外文献[7]提出将油中气体浓度水平、气体增长率和DGA解释结果结合起来,以提高变压器故障严重程度的判断准确率,但在此过程中并未涉及故障时内部能量的变化情况。

考虑到电力变压器内部所发生故障的严重程度与故障时产生的特征气体所含能量的大小之间有密切关系,文章首先利用故障特征气体借助焓变理论构造出计算故障能量系数的公式,为故障赋予一定的权值系数;然后以变压器热故障为例,将收集到的563组热故障特征气体所计算出的能量系数值作为研究对象,结合最大熵原理,从统计学的角度来分析这组能量系数的分布情况,最终得到最符合实际分布的热故障能量系数值概率密度函数,进而求取其概率分布函数,并以概率分布函数的分位值Q20、Q70和Q95作为电力变压器热故障严重程度比较基准值,从而实现对电力变压器热故障的严重性评估,以便更好地服务于电力变压器的运维。

1 电力变压器故障能量系数

1.1 变压器油热解模型

绝缘油中通常由三种主要的碳氢化合物组成,即链烷烃、环烷烃,此外还有芳香烃[8]。其中链烷烃较另外两种烃分子相比,其分子结构不稳定,更易发生氧化裂解反应,当电力变压器内部受到电、热或机械应力时,链烷烃首先发生分解,产生氢气和低分子烃类气体[9]。在研究变压器油分解时,有学者提出将正辛烷(C8H18)作为热分解过程的初级烃,但是在原油生产过程中,C8H18被脱除而忽略了其裂化反应所需的能量。通常变压器油分子中含有18～22个碳原子,因此将变压器油中碳原子最少的十八链烷烃(C18H38)作为故障特征气体最可能的产气来源,具体的化学反应方程式如式(1)～式(5)所示。由于热力学理论只对石油中的碳氢化合物分解起作用,而碳氧化合物对故障严重程度的评估贡献较小,故在此不作考虑[5]。

C18H38→CH4+C17H34

(1)

C18H38→C2H6+C16H32

(2)

C18H38→C2H4+C16H34

(3)

C18H38→C2H2+H2+C16H34

(4)

C18H38→H2+C18H36

(5)

1.2 焓变理论

基于溶解气体热力学方法的电力变压器故障严重性取决于从原油中释放故障气体所需的能量,利用焓变表示该能量。反应在一定条件下是吸热还是放热是由生成物和反应物的焓值差即焓变来体现,从宏观层面可表示为：

ΔH=H生-H反

(6)

式中H生、H反分别表示生成物、反应物焓的总值。ΔH>0表示吸热反应,ΔH<0表示放热反应。

在热力学中,焓变的确定通常要引入标准生成焓(ΔHf0)的概念,它表示在标准状态(压力为100 kPa,温度为298 K)下,由元素最稳定的单质生成1 mol纯化合物的反应热[10]。通过查阅有机分子热力学性质手册[11]可确定涉及文中各种组分的标准生成焓数值如表1所示。

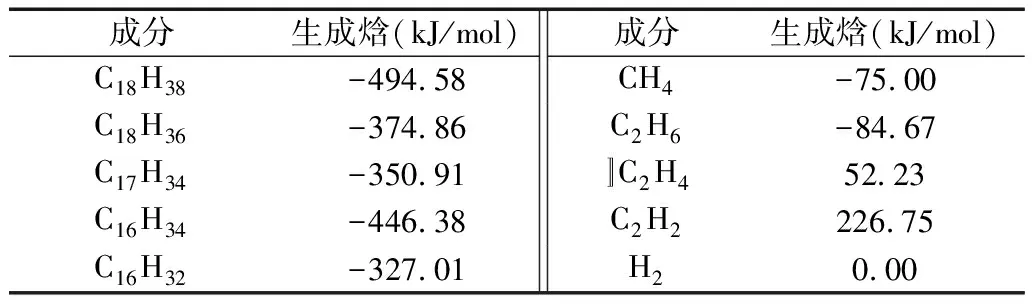
表1 各组分标准生成焓

1.3 能量系数

根据焓变的定义以及各组分标准生成焓的数据,可将生成不同故障特征气体所需的焓变值计算出来,例如对于式(5)而言,有：

ΔHH2=H(C18H36+H2)-HC18H38

(7)

将表1中相应数据代入式(7),可得生成H2的焓变值为119.72 kJ/mol;同理,根据式(1)～式(4)可计算出其他4种特征气体的生成焓,具体数值见表2。

表2 各故障特征气体生成焓

根据表2中的数据以及各故障特征气体浓度的百分比,可构造出计算故障能量系数(Ec)的公式如式(8)所示。由于故障气体的含量并不都是在298 K(室温25 ℃)时测得的,故还需进行温度校正。

(8)

式中x1,…,x5表示各特征气体生成焓的相对值;CCH4、CC2H6、CC2H4、CC2H2表示各特征气体浓度占总烃浓度的百分比;由于H2的产气来源有多种,较其他几种烃类气体含量高,故CH2表示H2浓度占H2与总烃浓度之和的百分比,T表示环境温度。

2 基于能量系数的电力变压器热故障严重程度评估

故障能量系数的使用有助于量化故障的严重程度,特别是在多台变压器遭受同一故障类型的情况下[12]。经统计分析,故障性质不同,其能量系数能级不同。故文中以变压器热故障性质为例,根据实际运行中油色谱分析结果计算能量系数值,建立电力变压器热故障严重程度评估分级参考基准值。

2.1 最大熵原理

熵的概念来源于热力学,通常衡量分子状态的混乱度。在信息论中,熵可以表征随机事件的信息量或不确定度,而随机事件不确定性的大小可用概率分布函数来描述,故信息论之父C. E. Shannons首次用数学语言阐明了概率与信息量之间的关系[13-14]。

设X为一个离散型随机变量,其取值集合为{xi},i=1,2,…,n,并且xi之间相互独立。假设pi代表随机事件xi的概率,那么对于事件xi,其传递的信息量可表示为：

(9)

式中r一般取值为2,此时的单位为bit;也可取其它对数底,采用其它相应单位,不同对数底之间可用对数公式相互换算。

由概率论可知,对X所有可能取值的信息量求其统计平均值,即可得到其平均自信息。当X为信源时,H(X)表示信源的平均自信息,即信息熵,表达式为：

(10)

在实际的未知分布中,一般只能了解其部分信息,将这部分信息作为该分布的约束条件,选取使信息熵达到最大的分布规律,即最符合实际的合理分布,这就是最大熵原理[15],可表示为：

(11)

(12)

式中fi表示随机变量X的第i个特征函数;fk表示随机变量X的k阶原点矩。

2.2 能量系数概率密度函数

为研究电力变压器热故障能量系数的分布规律,从山东某电网公司及往年的公开文献中共收集了600组过热故障油色谱数据[16],去掉信息不完整以及由于人为或外部因素而造成的异常数据,共563组有效的电力变压器热性故障油色谱数据。

将563组热性故障油色谱分析数据代入到式(8)中,计算出每组的能量系数,并将其作为样本数据,这组样本数据是连续分布的,其概率密度函数设为f(x),那么根据信息熵的定义可得式(13),由最大熵原理及连续随机变量的约束条件可得式(14)和式(15)：

(13)

(14)

(15)

式中Mi为样本数据的i阶原点距,可由实际数据得到,一般取4～5阶,文中i取值为5。

采用拉格朗日乘数法将求解概率密度函数的约束优化问题转化为无约束优化问题,经推导其最大熵分布的概率密度函数表达式为：

(16)

式中λ0, … ,λi为拉格朗日乘子。

只需求出式(16)中的拉格朗日乘子,即求得式(17)所示函数R取得最小值的未知参数,概率密度函数表达式即可确定：

(17)

采用非线性最小二乘法(L-M优化算法)拟合求解式(17),得到的未知参数值代入式(16),从而得到基于最大熵原理的热故障能量系数概率密度函数表达式。L-M优化算法相较于其他优化算法更具有鲁棒性,它可以快速达到最优点。通常来说数据都具有正态分布的特点,即数据会集中分布于某一段区间,而在此区间外分布的概率非常小,所以通过降噪去除部分概率分布的极小点,从而优化求解概率密度函数。

利用MATLAB对实测油色谱分析数据所计算出的能量系数值进行处理,得到其频率分布直方图如图1所示。经过降噪处理后,在MATLAB中拟合得到的最符合电力变压器热故障能量系数实际分布规律的概率密度函数曲线如图2所示,拟合得到的概率密度函数中各未知参数具体数值如表3所示。

图1 热故障能量系数值频率分布直方图

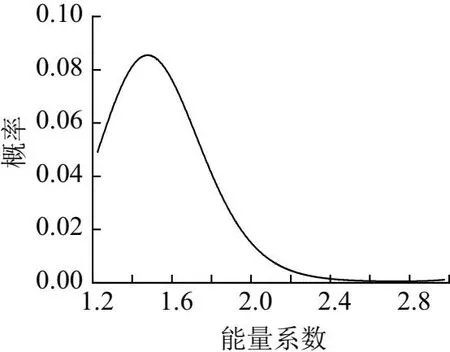
图2 能量系数概率密度函数曲线图

表3 概率密度函数各参数取值

反映能量系数值概率密度函数曲线拟合效果的指标有：误差平方和(SSE)、均方差(MSE)、均方根(RESE)以及确定系数(R2),各指标具体数值如表4所示。

表4 拟合曲线指标

表4中,SSE、MSE以及RESE的数值越接近于0越符合要求;R2的值越接近于1,表示拟合效果越好。因此,利用最大熵原理拟合出的能量系数值概率密度函数曲线可以反映变压器热故障的实际分布情况。

2.3 热故障严重程度分级基准

通过热故障能量系数的概率密度函数曲线,进一步得出其概率分布曲线如图3所示,将其转化为散点图,并依据散点图中各段斜率的差异性,利用Origin中的制图功能绘制出电力变压器热故障严重程度分级线段如图4所示。

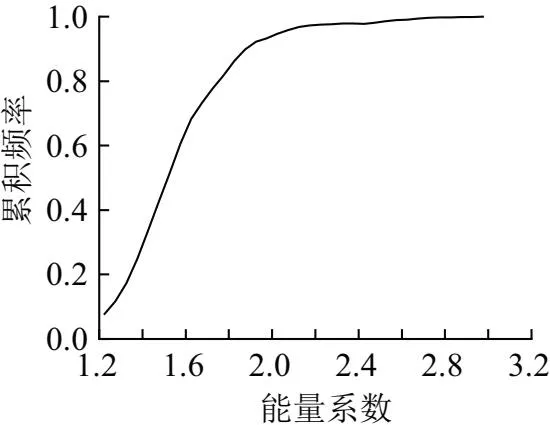
图3 能量系数概率分布曲线

图4 能量系数概率分布曲线分段图

从图4中可以看出该曲线有四个级别的变化率,由于变压器所发生故障的严重程度大部分集中在轻度或中等阶段,在其发展为严重或非常严重阶段之前大多已被发现并加以消除,故前者较后者所占比例较大,所以选取图4中线段交点,即分位点Q20、Q70和Q95所对应的能量系数值作为热故障严重程度的分级基准值。具体情况与数值如图5及表5所示。

图5 热故障严重程度划分示意图

表5 热故障严重程度分级基准

根据统计学原理可得,表5中Q95代表有95%的电力变压器热故障能量系数会低于该值,而只有5%的热故障能量系数会高于该值;Q70表示有70%的电力变压器热故障能量系数会低于该值,而只有30%的热故障能量系数会高于该值;以此类推。若根据电力变压器的某次热故障油色谱分析结果所计算出的能量系数值高于Q95,则认为该次故障程度为非常严重,若某次故障的能量系数值高于Q70而低于Q95,则认为该次热故障程度为严重,以此类推,具体情况如表6所示。

表6 热故障严重程度等级划分

通过热故障能量系数分级基准值,可以在对电力变压器故障定性分析的基础上,有效评估该次故障的严重性情况,直观地反映故障发展等级,为检修人员提供一种清晰、可靠的评估结果,从而采取针对性检修策略并做出相应的维护计划。

3 实例分析

案例1：某110 kV变电站 #2主变出厂日期为2018.06.03,投运日期为2019.01.15,产品型号为SZ11-50 000/110。

该变压器投运后,变电检修人员按照规程要求对变压器送电后的第1天、第4天、第10天和第30天取油样进行了色谱分析,试验结果均显示正常。一直至同年12月23日,对该主变例行取油样,温度矫正后发现本体油中出现乙炔,含量为1.64 μL/L,总烃含量已达358 μL/L,故障特征气体的具体数据如表7所示。对12月23日的油样利用IEC三比值法判断故障类型,诊断结果为高温过热故障。12月28日对该主变进行停电检修试验,发现变压器铁芯与夹件短接,导致铁芯多点接地,铁芯运行接地电流高达85 A ,远超规程中规定的小于0.1 A的要求。

表7 案例1中的油色谱分析具体数据(温度校正后)

案例2：某变电站 #1主变型号为SZ11-63 000/110,出厂日期为2012年3月,投运日期为2012年7月。

2019年3月26日,试验人员对该 #1主变及有载调压开关取油样进行色谱分析时,发现本体绝缘油中H2、C2H2等关键指标含量均有增加,再次取油样分析结果无明显差别,油色谱检测结果如表8所示。利用IEC三比值法进行深入分析,诊断该变压器存在高温过热故障,故变电检修室申请停电计划,于4月2日对该主变进行停电试验,最终检查结果为A相有载调压开关的选择开关第2档动静触头接触不良,致使电阻增大而过热。经打磨处理后,重新进行高压侧直流电阻测试,其结果合格,于4月23日再次取油样,色谱分析数据恢复正常。

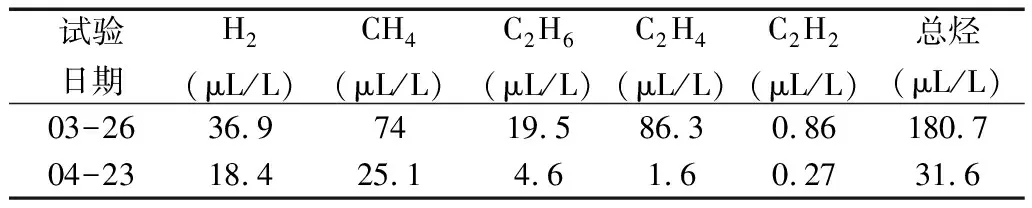
表8 案例2中油色谱数据(温度校正后)

案例3：某220 kV变电站 #2主变出厂日期为2016年9月,投运日期为2017年3月,型号为SFSZ11-240 000/220。

2019年11月7号,电气试验班对该变电站 #2号主变进行本体油色谱分析试验,发现绝缘油中溶解气体总烃含量已超出试验规程中所规定150 μL/L的注意值。随后试验班在同月8日-10日分别对 # 2主变本体取油样进行色谱分析,结果无明显差别,具体数据如表9所示。利用IEC三比值法对11月7号的油样进行判断,诊断该变压器内部存在大于700 ℃的高温过热故障。经一系列检查后发现,由于内部电抗器漏磁在其邻近的结构件中产生大量的涡流损耗,从而导致该主变内部出现高温过热现象。

表9 案例3中油色谱数据(温度校正后)

通过对以上三起故障案例分析,发现其故障类型均为高温过热故障。对这三起故障分别计算其各自的能量系数,并按照表6的热故障严重程度等级进行划分,具体情况如表10所示。

表10 热故障能量系数对比

从表10中可以看出,三起故障的性质虽同为高温过热故障,但其能量系数各不相同,故障严重性的等级也有所差别,案例3中对于漏磁引起的过热故障严重程度最大,案例1中铁芯多点接地故障次之,而案例2中有载分接开关触头接触不良的故障严重性最弱。借助所提的能量系数这一概念,可以在确定故障类型的基础上,为故障的严重程度赋予一种更直观的表达结果,有利于检修人员制定检修策略并作出相应的检修计划,以便更好地服务于电力变压器的运维工作。

4 结束语

文章借助油色谱分析数据对电力变压器热故障严重程度分析后,可得出以下结论：

(1)利用热力学中的焓变理论构造出计算能量系数的公式,并采用能量系数这一概念,可在利用传统与非传统方法对故障进行定性分析的基础上,为故障赋予一定的权值系数,将故障严重性量化为具体的数值;

(2)利用最大熵原理,从统计学的角度可实现对故障严重性的合理划分,且样本群越大,越能得出更具普适性的能量系数分级评估值;

(3)对变压器热故障能量系数的实际分布情况分析可得,即使故障属于同一类型,其严重程度也会有所不同,且所发生热故障的严重程度与经油色谱分析计算出的能量系数值呈正相关关系。