基于PCISPH的流体粒子飞溅改进方法

钮倩倩,林绿开,李 毅,2*

(1.温州大学 计算机与人工智能学院,浙江 温州 325000;2.浙江大学 计算机科学与技术学院,浙江 杭州 310058)

0 引 言

对于流体模拟研究经历了较长时间并不断衍生出新的方法。从宏观上来说,流体的模拟可分为基于物理的方法和非物理的方法。非物理的方法往往依赖于纯粹的数学模型,需要通过观测数据对实际数据进行建模,从而达到模拟仿真的效果,该类方法没有引入物理控制方程,所以结果通常存在动量、能量不守恒的问题。

基于物理的方法往往通过离散的数值方法对控制方程来进行求解。根据采样点的不同分布可以将其细分为欧拉方法和拉格朗日方法。欧拉方法是一种网格方法,典型的代表是有限差分方法[1],这种方法放弃了描述运动对象本身,转而描述运动对象所处空间场的变化。由于该方法相当于模拟了一种空间内固定的背景网格,通过运动对象对网格的影响来近似描述运动对象,所以不必考虑对象复杂的运动。拉格朗日粒子法是将客观世界中的流体看成由许多粒子组成的整体,该方法的基本思路是首先依照流体运动的物理定律,计算出粒子受到的外力和粒子之间的相互作用力,其次根据牛顿第二定律(Newton's Second Law of Motion-Force and Acceleration),计算出每个粒子在时间步长内的位置变化量,最后通过位置变化量来模拟出一段流体运动轨迹。主流的拉格朗日[2]粒子法包括 SPH(Smoothed Particle Hydrodynamics,光滑粒子流体动力学)[3-5]和PBF (Position Based Fluids,基于位置的流体模拟方法)[6]等。该文主要针对SPH进行研究。

SPH是一种基于积分插值理论的插值方法,通过离散采样点(粒子)来近似连续场量的值和导数,这些粒子自身携带某些场量,粒子处的场量通过从相邻粒子的值加权平均得到。有限差分法要求粒子排列在规则网格上,SPH则可以通过任意排布的粒子来求得近似。每个离散粒子都占据问题域的一小部分。

SPH源于计算天体物理学[7]领域,用于模拟天体物理现象。Desbrun等人[8]将SPH引入计算机图形学领域,用于模拟可变形体。Müller[9]将SPH引入流体模拟,并在此后扩展到各种问题的模拟。

在计算机图形学中,Solenthaler和Pajarola提出了一种有效的SPH变体,即PCISPH(Predictive-Corrective Incompressible SPH,预测校正不可压缩SPH)[10]。在这种SPH变化中,通过迭代预测和校正密度来增强不可压缩性。压力的确定应使压力能够减小密度波动。预测校正不可压缩SPH(PCISPH)允许更大的时间步长,如ISPH(隐式SPH)。此外,PCISPH解决了粒子级的不可压缩性,因此不需要求解泊松方程。预测校正不可压缩SPH(PCISPH)在一个模型中同时具有WCSPH(Weakly Compressible SPH,弱可压缩SPH)[11]和ISPH[12]的优点,即每次物理更新的计算成本低,时间步长大。通过流体传播估计的密度值,并以实现不可压缩性的方式更新压力。一旦达到每个单独粒子的先前用户定义的密度变化限制,传播就会停止。其中WCSPH是最直接的显式求解算法,基于连续性方程、动量方程和状态方程,直接计算作用在各个颗粒上的压力、体力、粘聚力和表面张力的合力,继而求出加速度进而结合边界条件进行速度位置的更新。

由于飞溅场景中流体的密度和压力的速率变化非常大,因此模拟对离散化解的精度要求很高。传统的不可压缩SPH[13]在许多场景中都有很好的性能,例如电影效果等。但由于数值耗散,通常不可能长期精确模拟流体的运动变化,在对数值精度要求较高的场景中仍有很大的改进空间。

该文提出一种基于PCISPH的流体粒子飞溅的改进方法。使用Taichi[14]框架实现流体仿真,太极编程语言大大提高了并行编程的生产力。

1 准备工作

1.1 不可压缩泊松方程模型

二维场景中自由表面流体的方程由质量守恒方程和动量守恒方程组成[15]。该文研究的是基于粒子的流体模拟,因此将控制方程转换为拉格朗日形式,如公式1和公式2所示。

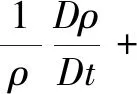
(1)

(2)

其中,ρ表示流体的密度,t是时间,u是流体的速度,P是压力,g是重力加速度,μ是剪切应力(包括粘滞力)。由于粘滞力的保留,式(1)和式(2)可以应用于牛顿流体和非牛顿流体。

1.2 速度预测

在纳维-斯托克斯(Navier-Stokes Equation)方程中,如果只考虑应力和重力,则从以下公式可以得到粒子的速度和位置。公式如下:

(3)

u*=ut+Δu*

(4)

r*=r+u*Δt

(5)

其中,ut和r表示粒子在时间t上的速度和位置。u*和r*表示预测步骤结束时粒子的中间速度和位置。Δu*表示预测期间粒子速度的变化量,Δt表示时间步长。

1.3 压力密度校正

方程1中的计算不能保证流体的不可压缩性,在X*位置处的密度ρ*由SPH得出:

(6)

其中,ri是起始粒子位置,rj是起始粒子的邻居粒子位置,mj是邻居粒子质量,h是光滑核函数半径。在密度ρ*和恒定的不可压缩流体密度ρ0之间存在偏差。

因此,校正步骤旨在将流体密度调整到初始值。在计算过程中,压力项将用于更新中间步骤中计算的粒子速度。公式如下:

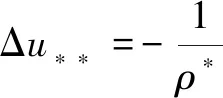
(7)

ut+1=u*+Δu**

(8)

其中,Δu**表示校正过程中粒子速度的变化量,ρ*表示预测步骤之后和校正步骤开始之前的中间密度,ut+1和Pt+1表示在时间t+1时刻的速度和压力值。

强制执行不可压缩性所需的压力项来自方程1,如下:

(9)

获得压力的泊松方程如下:

(10)

2 飞溅改进

压力校正。

由于预测校正不可压缩SPH(PCISPH)是从预测的密度变化中得出压力变化,因此计算密度变化是整个过程的核心。在SPH中密度计算如下:

(11)

其中,ri表示目标粒子位置,rj表示邻居粒子位置。

该文研究流体的飞溅场景。由于该场景中流体运动强烈,压力变化率和变化范围大,容易受到误差累积的影响。因此,提出了改进的泊松压力方程源项,如下所示:

(12)

其中,上标符号*表示在预测中计算所得。

将提出的密度变化解代入传统不可压缩流体的泊松压力方程,得到了改进的泊松压力方程式求解模型:

(13)

其中,ρ*表示预测中的流体密度。

公式12简化如下:

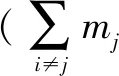
(14)

结合公式13和公式14得到:

(15)

(16)

又在预测校正不可压缩SPH(PCISPH)中通过预测密度变化来校正压力,公式如下:

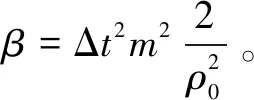
由公式16得:

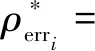
(18)

(19)

3 实验结果与分析

3.1 实验环境

该文利用 Python环境与编辑器,采用 Anaconda3集成Python3和Taichi环境,使用 PyCharm 代码编辑平台进行数据预处理以及后续网络框架的搭建与模型训练。

Taichi起步于 MIT 的计算机科学与人工智能实验室(CSAIL),设计初衷是便利计算机图形学研究人员的日常工作,帮助他们快速实现适用于 GPU 的视觉计算和物理模拟算法。Taichi 是嵌入于 Python的,使用即时编译(JIT)架构(如 LLVM,SPIR-V),将Python源代码转化为GPU或CPU的原生指令,在开发时和运行时均提供优越性能。Taichi的一大优势在于可移植性,支持多种后端。

3.2 实验对比

由于飞溅场景中流体密度和压力的变化率非常大,因此模拟对离散解的精度要求很高。针对基于粒子的流体仿真在模拟流体飞溅时的数值不稳定性,提出改进的泊松压力方程解,改进流体飞溅现象。将上文推导结果应用到模型中,得到改进后的流体模拟。下图是按时间顺序基于预测校正不可压缩SPH的粒子飞溅的传统方法和改进方法的效果对比。图1为8 000粒子数的飞溅效果对比,图2为4 000粒子数的飞溅效果对比。

图1 8 000粒子飞溅效果对比

图2 4 000粒子飞溅效果对比

表1是在8 000个粒子的三维流体模拟实验中,在GPU上进行了9个独立实验。

表1 在GPU上运行的实验数据 fps

基于NVIDIA和Windows平台,记录实验结果,如表1所示(fps表示程序运行帧率)。

图3是根据表1中的数据绘制出的折线图。其中实验编号表示时间先后顺序。从图中可以看出,在文中规定的测试环境下,传统方法和改进方法的帧率基本都处于45到60之间,但改进方法的帧率比传统方法的帧率略小一点,但是两种方法均达到实时性仿真效果的要求。

图3 基于GPU的实验程序性能比较

由上面效果比较可以看出,改进后的流体粒子飞溅较之前的传统流体粒子飞溅来说有所变化,改进后的飞溅的粒子更有规律性,符合现实中在重力作用下的效果。流体仿真模拟即要求仿真模拟结果更接近现实,改进后的更符合。从表1与图3可以看出模拟均达到实时仿真要求,但改进后的性能较之改进前的较差一点。

实验核心部分即为校正密度压力值,表2为传统方法中的密度误差和改进方法中的密度误差(数据选择来自传统方法和改进方法飞溅的粒子数量相差较多的情况)。

表2 校正密度误差值

图4是由表2数据绘制出的折线图,其中实验编号表示运行时间先后顺序。

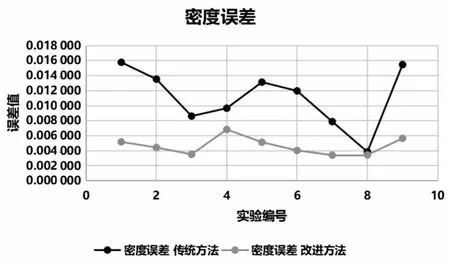
图4 校正的密度误差值对比

虽然改进后的帧率校之传统方法有所下降,但是基于PCISPH的流体仿真是通过预测校正密度压力值从而得到仿真效果。实验中通过改进密度误差从而改进压力值实现流体仿真,从表2和图4中可以看出,改进后的密度误差明显小于传统方法的密度误差,并且基本上在千分之五左右。改进后密度误差变小,增强了流体的不可压缩性,减小了压力噪声,得到了更真实、更稳定的飞溅仿真效果。从而验证了改进方法的有效性。

4 结束语

该文主要针对预测校正不可压缩SPH(PCISPH)流体仿真进行粒子飞溅改进,针对改进减小密度误差,增强流体的不可压缩性,减小了压力噪声,从而得到了优于原模型的仿真效果。但是该模型也存在相应的问题,模型不够稳定,该文添加较多粒子来减小不稳定带给实验结果的影响,在未来将对这些方面进行深入研究,以达到稳定且较大时间步长的流体模拟。同时,该文没有对该模型进行渲染,未来将对模型进行渲染。