基于多尺度特征融合的图像压缩感知重构

何卓豪，宋甫元，陆 越

（1.南京信息工程大学 数字取证教育部工程研究中心；2.南京信息工程大学 计算机学院、网络空间安全学院，江苏 南京 210044）

0 引言

压缩感知（Compression Sensing，CS）是由Donoho［1］提出的一种新的采样方式，采样过程即为压缩，该方式突破了奈奎斯特采样定理的限制，能更高效采样信号。CS 证实当信号在某个变换域为稀疏时，可构建一个测量矩阵Φ获得较少的测量值，并通过测量值反向恢复原始信号。

在图像压缩感知研究中，基于优化的CS 重构方法最早开展了工作。Gan［2］基于块的CS 重构分割图像后进行采样压缩，以减少所需内存与计算量。Mun 等［3］将方向变换与块压缩结合以提升图像重构质量。Gao 等［4］针对图像局部光滑特性，提出降低采样矩阵复杂度的局部结构测量矩阵，提升了压缩效率。Dong 等［5］提出NLR-CS 对图像进行非局部块匹配，并低秩优化相似块集合，利用图像的结构稀疏性提升图像恢复质量。Metzlerdamp 等［6］提出基于降噪的近似消息传递算法，在迭代中加入噪声修正项以提升重构质量。然而，传统方法需要大量的迭代计算，图像重构时间较长且在低采样率下重构的图像质量较差。

近年来，深度学习对图像特征的学习为目标检测［7］、图像分类［8］、图像超分辨率重构［9］、图像压缩感知方向等图像视觉领域提供了新的方法。ReconNet 证明了使用卷积神经网络（Convolutional Neural Network，CNN）恢复图像的可能性［10］，网络共有两个卷积模块，每个卷积模块有3个卷积层，卷积核大小分别为11、7、1。DR2-Net 在Recon-Net 基础上进行改进，使用残差网络与线性映射层进一步提升了图像重构质量［11］。Lian 等［12］在DR2-Net 基础上进行改进，在重构网络中使用多尺度残差网络与扩张卷积，学习图像不同尺度的信息并增大网络感受野。CSNet 使用卷积网络训练测量矩阵优化采样过程［13］。CSNet+设计了3 种类型的采样矩阵进一步优化采样过程［14］。ISTA-Net将基于优化迭代算法与神经网络结合，提升了网络的可解释性［15］。LDAMP 将神经网络与近似消息传递算法结合，去噪效果相较于较近似消息传递方法具有明显提升［16］。然而，目前基于深度学习的算法对图像特征的学习能力较弱，并未充分利用网络所有层次特征，在较低采样率下图像纹理复杂区域中的恢复较差。

注意力机制与许多图像视觉方向均有联系，不少研究发现，加入注意力机制有助于网络更好地学习图像特征，提升实验效果。Anwar 等［17］提出基于注意力机制的图像超分辨率重构网络，利用特征注意力与通道间依赖性调整通道特征，增强了网络学习能力。Zhang 等［18］将残差网络与密集网络结合，提出残差密集模块（Residual dense block，RDB），可充分利用所有层次特征提升图像重构质量。Fu 等［19］提出一种新的注意力融合方式，能自适应地结合网络局部特征与其全局相关性。Sagar 等［20］在DANet的基础上加入Channel Shuffle，在保证网络精度的前提下进一步提升了计算速度。此外，图像视觉领域内的研究可互相学习，以上工作在网络上的创新同样能帮助其他方面的网络进行提升。

本文提出一个新的基于多尺度注意力融合的图像CS重构网络。首先使用多尺度残差模块捕捉更多尺寸信息；然后设计并联的RDB 学习更密集的特征，增强特征利用率；最后利用双注意力融合模块，融合每个多尺度残差块的空间注意力与密集残差块的通道注意力，结合每个块的局部特征与全局相关性、浅层特征和深层特征，为高级特征补充更多低层特征空间信息，提升网络学习能力。

1 多尺度特征融合的图像重构模型

本文受DMASNet［20］与多尺度残差网络MSRN［21］的启发，提出基于基于块的CS 重构网络的多尺度注意力融合的图像压缩感知重构模型，如图1 所示。重构网络分为3个模块，首先通过全连接层完成图像初始化重构，得到原始图像块xi的近似解，然后通过后续网络层学习xi与的残差di，最后将xi与di相加得到最终的重构图像。

1.1 采样

本文基于块的压缩并非基于图像级别，因此有利于节省内存与计算量。如图1 所示，输入图像被分割为N个尺寸为33×33 的图像块，图像块xi被向量化为108 9×1 的向量。输入的图像块可表示为xi=[x1，x2，…，xn-1，xn]T，对于一个信号x∈Rn×1可取满足RIP［1］特性的随机测量矩阵Φ∈Rm×n。例如，高斯随机矩阵、伯努利随机矩阵等。将x投影到m维的低维，图像块的测量值yi=[y1，y2，…，ym-1，ym]T，采样过程表示为：

1.2 多尺度残差模块

网络首先使用一个完全连接层，从采样得到的测量值yi中获取图像块的初始重构，并将其输入多尺度残差模块，如图2 所示。为了学习不同尺寸的图像特征，残差块拥有3 条不同尺寸卷积核的支路，各支路使用特征级联（Concat），然后将特征输出到三支路使支路信息相互共享。最后一层使用大小为1 的卷积核将通道数缩减至输入时的通道数，以此串联多个多尺度残差模块，具体数学表达式为：

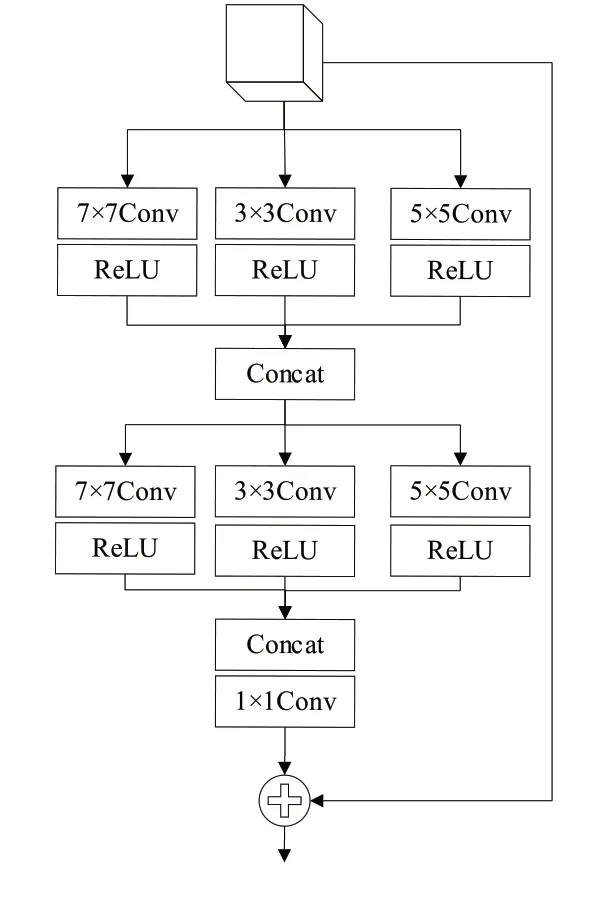
Fig.2 Multi-scale residual block图2 多尺度残差模块

式中：f res表示多尺度残差模块的函数；j表示第j个多尺度残差模块。

1.3 残差密集模块

DenseNet［22］的网络学习过程可传递上一层信息，加强特征利用率，RDB 在此基础上能提取局部密集特征。残差密集模块解释为设计的一个并联RDB，目的是让网络尽可能学习更密集的特征。如图3 所示，该模块接收了多尺度残差模块的输出，相较于RDN［18］组合的RDBs，并联结构能学习多尺度信息并减少网络深度。同时，模块拥有两个支路，卷积核尺寸大小分别为3、5，最后对两个支路的密集特征进行级联并通过1×1 卷积以减少通道数量，数学表达式为：

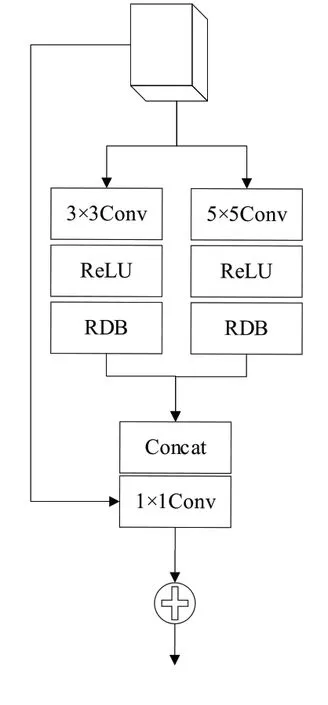
Fig.3 Residual dense block图3 残差模密集模块

式中：f RDB表示残差密集模块函数。

1.4 双注意力融合模块

融合空间注意力与通道注意力可使用串行［23］或并行［24］结构，受DMSANet［20］启发，通过双注意力融合每个模块的局部特征能充分利用网络所有层次特征，具体实现如图4 所示。通道注意力模拟了特征映射间的长期语义依赖，有选择性地加权每个的通道重要性，以捕获全局特征。空间注意力捕获多尺度残差模块的局部特征，根据空间注意力图选择性地聚合语义。双注意力融合将为高级特征补充更多低层特征空间信息，充分利用之前所有模块的局部特征信息结合浅层特征和深层特征，丰富类别信息的高级特征以利于像素定位。

Fig.4 Dual attention fusion block图4 双注意力融合模块

在通道注意力的计算过程中，对于输入为A∈RC×H×W表示的特征图，将A重塑为A∈RC×N、N=H×W，然后使用一个softmax 层获得通道注意力图x∈RC×C。

通道注意力特征的计算公式为：

式中：β为比例参数；E1j∈RC×H×W；C为通道数。

在空间注意力计算过程中，对于输入特征图A∈RC×H×W，在输入一个卷积层后得到两个特征映射B、C∈RC×H×W，将B、C重塑为RC×N，然后利用softmax 层计算得到空间注意图x∈RN×N，计算公式为：

之后，将特征A输入一个卷积层生成新的特征映射D∈RC×H×W，并重塑尺寸为RC×N、N=H×W，D、转置相乘得到融合空间信息后的特征图，空间注意力特征计算公式为：

式中：α为比例参数；E2j∈RC×H×W。

最后，将两个注意力特征级联，使用1×1 卷积减少通道数量。

1.5 图像重构

图像采样后的测量值yi作为网络输入，首先经过线性映射层得到初始重构图像，通过后续网络层逐渐提升重构质量，然后基于网络多尺度残差模块、残差密集模块及双注意力融合模块估计残差di。

网络中多尺度残差模块与双注意力融合模块的数量各为3 个，残差密集块的数量为1 个，卷积会使特征图数量增加，但模块输出通过1×1 卷积，始终保持在32 个通道数量，有利于提取局部特征和传递模块信息，便于模块在数量上的变动及与其他框架相结合。网络中除了最后一层，每一层卷积后都有Relu 函数，防止梯度丢失。初始重构与残差相加得到网络最终输出。重构过程可表示为：

综上，网络输出图像块会被重新拼接成完整的图像，网络损失函数为均方误差函数（Mean Squared Error，MSE），并使用Adam 优化网络参数。损失函数公式为：

式中：N为训练样本数量；xi为对应的原始图像块；为网络输出图像块。

2 实验结果与分析

网络训练、测试运行GPU 为GeForce GTX 1080 Ti，选取公共数据集BSD 500 的测试集［25］与训练集作为实验训练数据集，共400 张图像，训练时图像会被转为灰度图像。虽然，图像颜色空间会对目标检测与图像分类产生一定影响，但根据CS测量值恢复图像的影响较小。

因此，本文选取与比较算法一致的公共数据集Set11作为测试数据集，网络训练迭代120 轮，将初始学习速率设置为0.000 1，并在第40-80 轮时下降1/10。在0.01、0.04、0.1、0.25 采样率（Measurement Ratio，MR）下进行，采样使用高斯随机矩阵，图像被裁剪为33×33 大小的图像块，取步长为11，长度为1 089 的图像块向量在对应MR 下的测量值长度分别为10、43、109、272。采用图像的峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）与结构相似性（Structure Similarity Index Measure，SSIM）作为重构图像质量的评价指标，PSNR 与SSIM 值越高表示图像质量越好。

本文将所提方法与NLR-CS［5］、D-AMP［6］、Reconnet［10］、DR2Net［11］及MSRNet［12］方法进行比较。其中，前两者为基于优化迭代的算法，后3种为基于深度学习的算法。PSNR 为基于对应像素点误差的评价指标，是衡量有损压缩后图像重建质量的重要指标之一。由表1 可知，在不同算法下测试Set11 数据集中11 幅图像的PSNR，第5 组数据为11 幅图像在不同MR 下的平均PSNR，前4 组数据为4 幅图像的具体数据。相较于其他算法，本文算法在不同采样率下PSNR 值均较高，表明重构图像质量优于其他算法。

Table 1 PSNR values for different algorithms表1 不同算法的PSNR值

从人眼视觉标准而言，SSIM 评价指标同样重要。由表2 可知，本文算法在不同采样率下，SSIM 值均优于其他算法，证明了所提网络学习到了更多图像细节信息，重构图像拥有更好的视觉效果。由此可见，基于深度学习算法优于基于优化迭代的算法，拥有更好的前景，对图像特征学习能力更强的网络的图像重构质量越好。

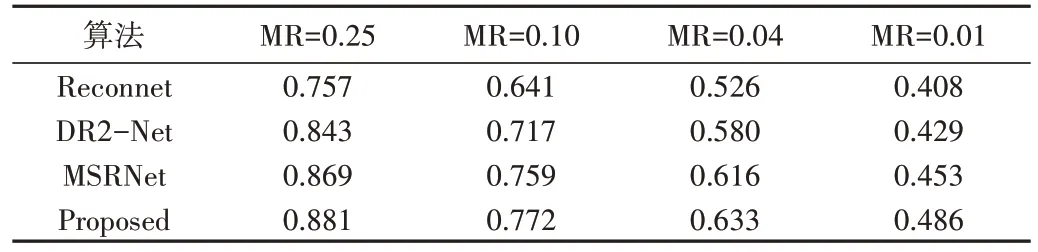
Table 2 SSIM values for different algorithms表2 不同算法的SSIM值

由表3可知，基于优化迭代的CS重构算法计算量较大，相较于基于深度学习的算法更耗费时间，基于深度学习算法的时间复杂度与重构网络大小相关，当网络为增强特征学习能力而加深时，计算量将随之增加。在相同实验环境下，本文算法相较于通过牺牲重构时间提升重构质量的MSRNet，运行速度更快，耗时远低于传统优化迭代算法。

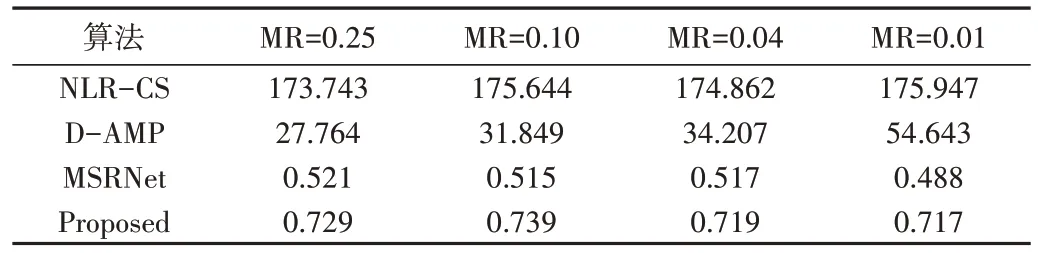
Table 3 Running time of reconstructing a single image（256×256）表3 重构一张图像（256×256）的运行时间（s）

图5 展示了测试数据集中4 幅图像在不同采样率下的重构结果，测试图片均为灰度图像。由此可见，本文算法在0.01 的采样率下仍具有一定可见度，证明所提网络在低采样率下重构性能良好，图像质量将随着采样率增加得到进一步提升。

Fig.5 Reconstruction results of 4 images under different MR图5 不同MR下的4张图像的重构结果

3 结语

本文提出一种新的基于多尺度注意力融合的图像CS重构网络，从图像初始重构过程中学习残差，以提升图像重构质量。为了充分利用网络所有层次特征，网络引入双注意力结构融合残差密集特征与多尺度残差特征，利用先前所有模块的局部特征信息结合浅层与深层特征，为高级特征补充更多低层特征空间信息。

实验表明，本文算法在性能上相较于传统方法更优。下一步，将在网络去噪、块效应与速度方面进行优化，并尝试在经典压缩感知算法基础上增加网络的可解释性。